Refine search
Actions for selected content:
3 results
10 - Bayesian Parameter Estimation and Reliability Updating
-
- Book:
- Structural and System Reliability
- Published online:
- 13 January 2022
- Print publication:
- 13 January 2022, pp 301-356
-
- Chapter
- Export citation
Estimation of the variance for the multitype Galton–Watson process
-
- Journal:
- Journal of Applied Probability / Volume 19 / Issue 2 / June 1982
- Published online by Cambridge University Press:
- 14 July 2016, pp. 408-414
- Print publication:
- June 1982
-
- Article
- Export citation
Estimation of the criticality parameter of a superitical branching process with random environments
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 890-896
- Print publication:
- December 1979
-
- Article
- Export citation
 and Becker estimator
and Becker estimator  are also proposed.
are also proposed.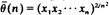 when
when 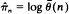 is a strongly consistent and asymptotically unbiased estimator for the criticality parameter
is a strongly consistent and asymptotically unbiased estimator for the criticality parameter