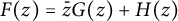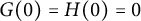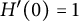Refine search
Actions for selected content:
3 results
3 - The Time-Independent Schrödinger Equation
-
- Book:
- A Computational Introduction to Quantum Physics
- Published online:
- 24 April 2024
- Print publication:
- 25 April 2024, pp 37-56
-
- Chapter
- Export citation
Landau-type theorems for certain bounded bi-analytic functions and biharmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 152-165
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
14 - Many-Atom Systems
-
- Book:
- Quantum Mechanics in Nanoscience and Engineering
- Published online:
- 11 May 2023
- Print publication:
- 01 June 2023, pp 237-285
-
- Chapter
- Export citation