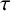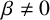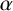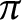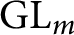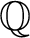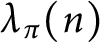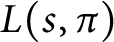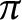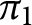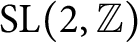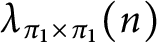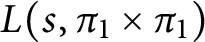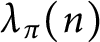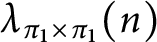Refine search
Actions for selected content:
5 results
ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 280-287
- Print publication:
- October 2022
-
- Article
- Export citation
Cancellation of two classes of dirichlet coefficients over Beatty sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 234-252
- Print publication:
- March 2022
-
- Article
- Export citation
SUMS OF MULTIPLICATIVE FUNCTIONS OVER A BEATTY SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 327-334
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Characterization of two-distance sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 198-218
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Beatty Sequences, Continued Fractions, and Certain Shift Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 19 / Issue 4 / 01 December 1976
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-482
- Print publication:
- 01 December 1976
-
- Article
-
- You have access
- Export citation