We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we compute the topological Hochschild homology of quotients of discrete valuation rings (DVRs). Along the way we give a short argument for Bökstedt periodicity and generalizations over various other bases. Our strategy also gives a very efficient way to redo the computations of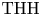 
$\operatorname {THH}$ (respectively, logarithmic 
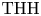$\operatorname {THH}$) of complete DVRs originally due to Lindenstrauss and Madsen (respectively, Hesselholt and Madsen).
