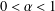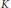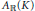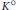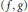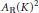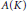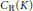Refine search
Actions for selected content:
5 results
Stabilization of the Kawahara–Kadomtsev–Petviashvili equation with time-delayed feedback
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 280-306
- Print publication:
- February 2025
-
- Article
- Export citation
Polynomial stability of a piezoelectric beam with magnetic effect and a boundary dissipation of the fractional derivative type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 23-53
-
- Article
- Export citation
THE CONTROLLER DESIGN FOR SINGULAR FRACTIONAL-ORDER SYSTEMS WITH FRACTIONAL ORDER 0 <α< 1
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 25 September 2018, pp. 230-248
-
- Article
-
- You have access
- Export citation
EXPONENTIAL STABILISATION OF A TREE-SHAPED NETWORK OF STRINGS WITH VARIABLE COEFFICIENTS*
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 10 March 2011, pp. 481-499
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Reducibility in A ℝ(K), C ℝ(K), and A(K)
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 3 / 01 June 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 646-667
- Print publication:
- 01 June 2010
-
- Article
-
- You have access
- Export citation