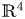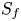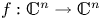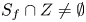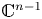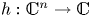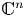Refine search
Actions for selected content:
14 results
Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$
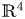
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1045-1070
- Print publication:
- June 2023
-
- Article
- Export citation
Envelopes of families of framed surfaces and singular solutions of first-order partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1515-1542
- Print publication:
- October 2021
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
Evolutes and focal surfaces of framed immersions in the Euclidean space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 497-516
- Print publication:
- February 2020
-
- Article
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
Geometric Interpretation of Lagrangian Equivalence
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 806-812
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
Minkowski Symmetry Sets of Plane Curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 461-480
-
- Article
- Export citation
Geometric Invariants of Cuspidal Edges
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-462
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
ON SMOOTH MAPS WITH FINITELY MANY CRITICAL POINTS: ADDENDUM
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 231-236
- Print publication:
- February 2006
-
- Article
- Export citation
THE GROUP OF IMMERSIONS OF HOMOTOPY $(4k-1)$-SPHERES
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 30 January 2006, pp. 163-176
- Print publication:
- February 2006
-
- Article
- Export citation
Degeneracy of 2-Forms and 3-Forms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 4 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-560
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
Regular homotopy classes of singular maps
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 22 April 2005, pp. 738-762
- Print publication:
- May 2005
-
- Article
- Export citation
Singularities of centre symmetry sets
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 16 December 2004, pp. 132-166
- Print publication:
- January 2005
-
- Article
- Export citation
ON SMOOTH MAPS WITH FINITELY MANY CRITICAL POINTS
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 24 May 2004, pp. 783-800
- Print publication:
- June 2004
-
- Article
- Export citation