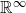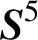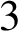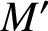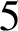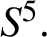Refine search
Actions for selected content:
8 results
Pin±-structures on non-oriented 4-manifolds via Lefschetz fibrations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decoupling Decorations on Moduli Spaces of Manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 163-198
- Print publication:
- January 2023
-
- Article
- Export citation
A NOTE ON OPEN BOOK EMBEDDINGS OF
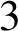 $3$-MANIFOLDS IN
$3$-MANIFOLDS IN 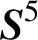 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 499-506
- Print publication:
- June 2022
-
- Article
- Export citation
James bundles
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 89 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 30 June 2004, pp. 217-240
- Print publication:
- July 2004
-
- Article
- Export citation
A note on the theta characteristics of a compact Riemann surface
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-424
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Twistor spaces and the adiabatic limits of Dirac operators
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 53-73
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Seiberg-Witten Invariants of Lens Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 4 / 01 August 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 780-808
- Print publication:
- 01 August 2001
-
- Article
-
- You have access
- Export citation
Nonexistence of Almost-Quaternion Substructures on the Complex Projective Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 231-232
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation