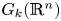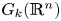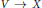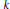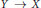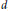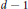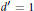Refine search
Actions for selected content:
6 results
Equivariant parametrized topological complexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
- Export citation
Corrigendum to “Topological complexity of real Grassmannians”
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 19 April 2022, pp. 1071-1072
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
Topological complexity of real Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 2013-2029
- Print publication:
- December 2021
-
- Article
- Export citation
Splitting definably compact groups in o-minimal structures
-
- Journal:
- The Journal of Symbolic Logic / Volume 76 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 12 March 2014, pp. 973-986
- Print publication:
- September 2011
-
- Article
- Export citation
Embedding Coverings in Bundles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 1 / 01 March 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-55
- Print publication:
- 01 March 1999
-
- Article
-
- You have access
- Export citation
Nonexistence of Almost-Quaternion Substructures on the Complex Projective Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 231-232
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation