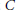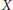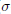Refine search
Actions for selected content:
8 results
Moduli of local uniform rotundity for convex bodies in normed spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. 1251-1261
- Print publication:
- December 2025
-
- Article
- Export citation
Higher Connectedness Properties of Support Points and Functionals of Convex Sets
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1236-1254
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Measure Convex and Measure Extremal Sets
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 4 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 536-548
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
A New Characterization of Hardy Martingale Cotype Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 4 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-491
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
Intrinsic volumes and Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 354-364
- Print publication:
- June 2001
-
- Article
- Export citation
The convex hull of samples from self-similar distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 34-47
- Print publication:
- March 1999
-
- Article
- Export citation
Principe du Maximum et Lemme de Schwarz a Valeurs Vectorielles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 3 / 01 September 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 356-363
- Print publication:
- 01 September 1997
-
- Article
-
- You have access
- Export citation
Positive Polynomials and Time Dependent Integer-Valued Random Variables
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 1 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-41
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation