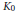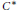Refine search
Actions for selected content:
4 results
UNBOUNDED HERMITIAN OPERATORS ON KOLASKI SPACES
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 August 2013, pp. 507-517
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Strongly Perforated
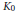 ${{K}_{0}}$ -Groups of Simple
${{K}_{0}}$ -Groups of Simple 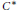 ${{C}^{*}}$ -Algebras
${{C}^{*}}$ -Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 3 / 01 September 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 457-472
- Print publication:
- 01 September 2003
-
- Article
-
- You have access
- Export citation
Classification of Atomic Facially Symmetric Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 1 / 01 February 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-87
- Print publication:
- 01 February 1993
-
- Article
-
- You have access
- Export citation
Locally Uniformly Rotund Renorming and Injections Into c0(Γ)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 494-500
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation