Refine search
Actions for selected content:
4 results
Global smooth solutions and singularity formation for the relativistic Euler equations with radial symmetry
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-32
-
- Article
- Export citation
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 172-183
- Print publication:
- August 2025
-
- Article
- Export citation
Regularity at space-like and null infinity
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-208
- Print publication:
- January 2009
-
- Article
- Export citation
A Weighted
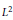 ${{L}^{2}}$ -Estimate of the Witten Spinor in Asymptotically Schwarzschild Manifolds
${{L}^{2}}$ -Estimate of the Witten Spinor in Asymptotically Schwarzschild Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 943-965
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation