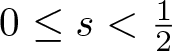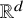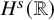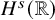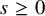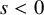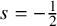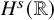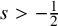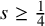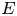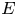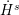Refine search
Actions for selected content:
34 results
A remark on the well-posedness of the modified KdV equation in L2
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-26
-
- Article
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp well-posedness for the cubic NLS and mKdV in
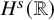 $H^s({{\mathbb {R}}})$
$H^s({{\mathbb {R}}})$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stabilization of the Kawahara–Kadomtsev–Petviashvili equation with time-delayed feedback
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 280-306
- Print publication:
- February 2025
-
- Article
- Export citation
Periodic and solitary waves in a Korteweg–de Vries equation with delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 176-198
- Print publication:
- February 2025
-
- Article
- Export citation
Long-time asymptotics of the modified KdV equation in weighted Sobolev spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 August 2022, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation
Resonance-based schemes for dispersive equations via decorated trees
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE INSTABILITY OF PERIODIC WAVES FOR DISPERSIVE EQUATIONS—REVISITED
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 471-493
- Print publication:
- September 2022
-
- Article
- Export citation
Dispersive fractalisation in linear and nonlinear Fermi–Pasta–Ulam–Tsingou lattices
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 820-845
-
- Article
-
- You have access
- Open access
- Export citation
A LIPSCHITZ METRIC FOR THE CAMASSA–HOLM EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 May 2020, e27
-
- Article
-
- You have access
- Open access
- Export citation
Existence of multi-travelling waves in capillary fluids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 2905-2936
- Print publication:
- December 2020
-
- Article
- Export citation
GLOBAL ATTRACTOR FOR WEAKLY DAMPED, FORCED mKdV EQUATION BELOW ENERGY SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 20 June 2019, pp. 171-203
- Print publication:
- March 2021
-
- Article
- Export citation
The Korteweg–de Vries, Burgers and Whitham limits for a spatially periodic Boussinesq model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 191-217
- Print publication:
- February 2019
-
- Article
- Export citation
On the well-posedness and asymptotic behaviour of the generalized Korteweg–de Vries–Burgers equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 219-260
- Print publication:
- February 2019
-
- Article
- Export citation
Bifurcations and Single Peak Solitary Wave Solutions of an Integrable Nonlinear Wave Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1084-1098
- Print publication:
- December 2016
-
- Article
- Export citation
New Non-Travelling Wave Solutions of Calogero Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1036-1049
- Print publication:
- December 2016
-
- Article
- Export citation
A Posteriori Error Estimates for Conservative Local Discontinuous GalerkinMethods for the Generalized Korteweg-de Vries Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 250-278
- Print publication:
- July 2016
-
- Article
- Export citation
Integrable Couplings of the Boiti-Pempinelli-Tu Hierarchy and Their Hamiltonian Structures
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 588-598
- Print publication:
- August 2016
-
- Article
- Export citation
On Invariant-Preserving Finite Difference Schemes for the Camassa-Holm Equation and the Two-Component Camassa-Holm System
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1015-1041
- Print publication:
- April 2016
-
- Article
- Export citation