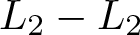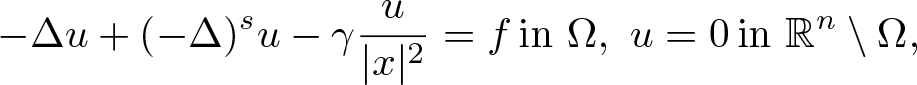Refine search
Actions for selected content:
9 results
Regular solutions to the dissipative Aw–Rascle system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional separation solutions of the sinh-Gordon type equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1-15
-
- Article
- Export citation
On mixed local–nonlocal problems with Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-34
-
- Article
- Export citation
Existence and two-scale convergence of the generalised Poisson–Nernst–Planck problem with non-linear interface conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 03 August 2020, pp. 683-710
-
- Article
-
- You have access
- Open access
- Export citation
Periodic pattern formation in the coupled chemotaxis-(Navier–)Stokes system with mixed nonhomogeneous boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 3121-3152
- Print publication:
- December 2020
-
- Article
- Export citation
An Inverse Source Non-local Problem for a Mixed Type Equation with a Caputo Fractional Differential Operator
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 417-438
- Print publication:
- May 2017
-
- Article
- Export citation
Quasi-Static Linear Thermo-Viscoelastic Process with Irregular Viscous Dissipation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 924-943
- Print publication:
- August 2017
-
- Article
- Export citation
The WASP Model: A Micro-Macro System of Wave-Schrödinger-Plasma Equations for Filamentation
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 2 / February 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 406-440
- Print publication:
- February 2011
-
- Article
- Export citation
LARGE-TIME BEHAVIOUR OF THE SOLUTIONS FOR A MULTIDIMENSIONAL NON-ISENTROPIC HYDRODYNAMIC MODEL FOR SEMICONDUCTORS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 02 February 2006, pp. 145-172
-
- Article
-
- You have access
- Export citation