Refine search
Actions for selected content:
11 results
Periodic solutions for one-dimensional nonlinear nonlocal problem with drift including singular nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 23 December 2021, pp. 229-261
- Print publication:
- February 2023
-
- Article
- Export citation
Hopf bifurcation from spike solutions for the weak coupling Gierer–Meinhardt system
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 113-145
-
- Article
- Export citation
Existence of multiple periodic solutions to a semilinear wave equation with x-dependent coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 04 June 2019, pp. 2586-2606
- Print publication:
- October 2020
-
- Article
- Export citation
Periodic solutions for a fractional asymptotically linear problem
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 593-615
- Print publication:
- June 2019
-
- Article
- Export citation
Coexistence Solutions for a Periodic Competition Model with Singular–Degenerate Diffusion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 1065-1075
-
- Article
- Export citation
Instability of periodic traveling waves for the symmetric regularized long wave equation
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 235-268
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Cylindrically symmetric travelling fronts in a periodic reaction—diffusion equation with bistable nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 28 August 2015, pp. 1053-1090
- Print publication:
- October 2015
-
- Article
- Export citation
Global Well-Posedness and Convergence Results for the 3D-Regularized Boussinesq System
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 6 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1415-1435
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
INHOMOGENEOUS PERIODIC PARABOLIC PROBLEMS WITH INDEFINITE DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 516-524
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
CONVERGENCE IN MONOTONE AND SUBHOMOGENEOUS DISCRETE DYNAMICAL SYSTEMS ON PRODUCT BANACH SPACES
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 13 August 2003, pp. 681-688
- Print publication:
- September 2003
-
- Article
- Export citation
Global Hypoellipticity of a Class of Second Order Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 3 / 01 September 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-305
- Print publication:
- 01 September 1994
-
- Article
-
- You have access
- Export citation
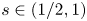

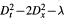 is globally hypoelliptic; in particular, we show that the addition of a term of order zero may destroy the property of global hypoellipticity of operators of principal type, contrary to that happens with the usual (local) hypoellipticity.
is globally hypoelliptic; in particular, we show that the addition of a term of order zero may destroy the property of global hypoellipticity of operators of principal type, contrary to that happens with the usual (local) hypoellipticity.