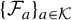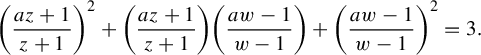Refine search
Actions for selected content:
5 results
Equidistribution for matings of quadratic maps with the modular group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 859-887
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remarks on quasi-Reinhardt domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 297-304
- Print publication:
- April 2019
-
- Article
- Export citation
Hartogs’ Theorem on Separate Holomorphicity for Projective Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 84-86
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
CR Mappings of Circular CR Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 4 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 396-407
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation
Some Properties of Bounded Holomorphic Mappings Defined on Bounded Homogeneous Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 3 / 01 September 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 358-364
- Print publication:
- 01 September 1986
-
- Article
-
- You have access
- Export citation