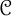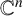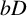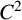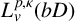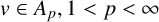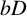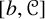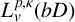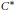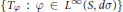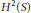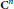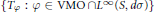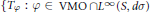Refine search
Actions for selected content:
3 results
BOUNDEDNESS AND COMPACTNESS OF CAUCHY-TYPE INTEGRAL COMMUTATOR ON WEIGHTED MORREY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 36-56
- Print publication:
- August 2022
-
- Article
- Export citation
MICROLOCAL REGULARITY FOR MIZOHATA TYPE DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1185-1209
- Print publication:
- July 2020
-
- Article
- Export citation
Singular Integral Operators and Essential Commutativity on the Sphere
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 889-913
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation