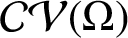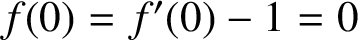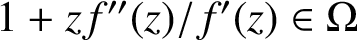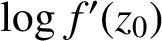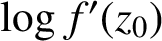Refine search
Actions for selected content:
5 results
AN APPLICATION OF SCHUR’S ALGORITHM TO VARIABILITY REGIONS OF CERTAIN ANALYTIC FUNCTIONS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 468-481
- Print publication:
- June 2022
-
- Article
- Export citation
Existence of extremal Beltrami coefficients with nonconstant modulus
-
- Journal:
- Nagoya Mathematical Journal / Volume 199 / September 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-14
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
ON INFINITESIMAL TEICHMÜLLER SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 293-300
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
CONVEX REGIONS IN THE PLANE AND THEIR DOMES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 18 April 2006, pp. 624-654
- Print publication:
- May 2006
-
- Article
- Export citation
LENGTH SPECTRUMS OF RIEMANN SURFACES AND THE TEICHMÜLLER METRIC
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 20 March 2003, pp. 247-254
- Print publication:
- March 2003
-
- Article
- Export citation