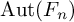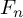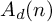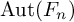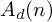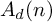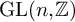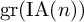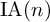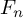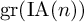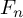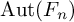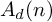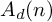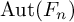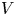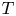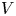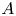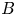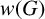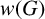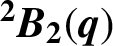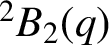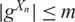Refine search
Actions for selected content:
19 results
On the degree-two part of the associated graded of the lower central series of the Torelli group
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-39
-
- Article
- Export citation
On finite groups with bounded conjugacy classes of commutators
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-6
-
- Article
- Export citation
Generalized torsion orders and Alexander polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 401-420
- Print publication:
- June 2025
-
- Article
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 830-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACTIONS OF AUTOMORPHISM GROUPS OF FREE GROUPS ON SPACES OF JACOBI DIAGRAMS. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1-69
- Print publication:
- January 2024
-
- Article
- Export citation
Irrational-slope versions of thompson's groups T and V
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 244-262
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Commutator length of powers in free products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 102-119
-
- Article
- Export citation
COMMUTATOR EQUATIONS IN FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 320-335
- Print publication:
- May 2022
-
- Article
- Export citation
ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 145-159
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- Export citation
COPRIME COMMUTATORS IN THE SUZUKI GROUPS
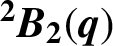 $^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
$^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 448-452
- Print publication:
- December 2021
-
- Article
- Export citation
ON FINITE-BY-NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 20 December 2019, pp. 54-58
- Print publication:
- January 2021
-
- Article
- Export citation
Profinite groups with restricted centralizers of commutators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 01 April 2019, pp. 2301-2321
- Print publication:
- October 2020
-
- Article
- Export citation
GROUPS WITH ABELIAN SYLOW SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 16 December 2009, pp. 43-47
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
GROUPS WITH COMMUTING POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 343-351
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
NEW OBSTRUCTIONS FOR THE SURJECTIVITY OF THE JOHNSON HOMOMORPHISM OF THE AUTOMORPHISM GROUP OF A FREE GROUP
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 25 October 2006, pp. 341-360
- Print publication:
- October 2006
-
- Article
- Export citation
Cohomological characterization of the Hilbert symbol over Q*p
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-368
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
ON EXTENSIONS OF GROUPS OF FINITE EXPONENT
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 3 / September 2003
- Published online by Cambridge University Press:
- 10 September 2003, pp. 535-538
- Print publication:
- September 2003
-
- Article
-
- You have access
- Export citation
A Basis of Bachmuth Type in the Commutator Subgroup of a Free Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 2 / 01 June 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 299-303
- Print publication:
- 01 June 2003
-
- Article
-
- You have access
- Export citation
On the lower central factors of free centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-75
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation