A profinite group $G$ of finite cohomological dimension with (topologically) finitely generated closed normal subgroup $N$ is studied. If $G$ is pro-$p$ and $N$ is either free as a pro-$p$ group or a Poincaré group of dimension 2 or analytic pro-$p$, it is shown that $G/N$ has virtually finite cohomological dimension ${\rm cd}(G)\,{-}\,{\rm cd}(N)$. Some other cases when $G/N$ has virtually finite cohomological dimension are also considered.
If $G$ is profinite, the case of $N$ projective or the profinite completion of the fundamental group of a compact surface is considered.
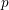 $p$-group
$p$-group