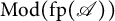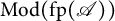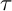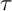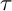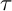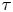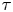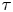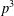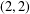Refine search
Actions for selected content:
21 results
Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-27
-
- Article
- Export citation
A symmetry of silting quivers
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 July 2023, pp. 687-696
- Print publication:
- September 2023
-
- Article
- Export citation
MINIMAL (
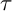 $\tau $-)TILTING INFINITE ALGEBRAS
$\tau $-)TILTING INFINITE ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 221-238
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Report on the finiteness of silting objects
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 217-233
-
- Article
- Export citation
τ-Tilting finite cluster-tilted algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 950-955
-
- Article
- Export citation
Coxeter Diagrams and the Köthe’s Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 656-686
- Print publication:
- June 2021
-
- Article
- Export citation
TAME BLOCK ALGEBRAS OF HECKE ALGEBRAS OF CLASSICAL TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 September 2019, pp. 179-201
- Print publication:
- October 2021
-
- Article
- Export citation
ALGEBRAS OF GENERALIZED DIHEDRAL TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 181-236
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
Fields of Definition for Representations of Associative Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 22 November 2018, pp. 291-304
-
- Article
- Export citation
COHOMOLOGICAL LENGTH FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 223 / Issue 1 / September 2016
- Published online by Cambridge University Press:
- 18 August 2016, pp. 136-161
- Print publication:
- September 2016
-
- Article
-
- You have access
- HTML
- Export citation
THE DIMENSION OF A SUBCATEGORY OF MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 09 October 2015, e19
-
- Article
-
- You have access
- Open access
- Export citation
ON SEMIGENERIC TAMENESS AND BASE FIELD EXTENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 39-53
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
THE CLASS OF (2, 2)-GROUPS WITH HOMOCYCLIC REGULATOR QUOTIENT OF EXPONENT
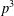 $p^{3}$ HAS BOUNDED REPRESENTATION TYPE
$p^{3}$ HAS BOUNDED REPRESENTATION TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 December 2014, pp. 12-29
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
On self-injective algebras of stable dimension zero
-
- Journal:
- Nagoya Mathematical Journal / Volume 203 / September 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-108
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
DERIVED EQUIVALENCE CLASSIFICATION OF SYMMETRIC ALGEBRAS OF POLYNOMIAL GROWTH
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 08 December 2010, pp. 277-291
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
An Uncountably Infinite Number of Indecomposable Totally Reflexive Modules
-
- Journal:
- Nagoya Mathematical Journal / Volume 187 / September 2007
- Published online by Cambridge University Press:
- 11 January 2016, pp. 35-48
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Endomorphism Rings of Finite Global Dimension
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 2 / 01 April 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 332-342
- Print publication:
- 01 April 2007
-
- Article
-
- You have access
- Export citation
Infinite Dimensional Representations of Canonical Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 1 / 01 February 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 180-224
- Print publication:
- 01 February 2006
-
- Article
-
- You have access
- Export citation
The Theorem of Bo Chen and Hall Polynomials
-
- Journal:
- Nagoya Mathematical Journal / Volume 183 / 2006
- Published online by Cambridge University Press:
- 11 January 2016, pp. 143-160
- Print publication:
- 2006
-
- Article
-
- You have access
- Export citation
Forbidden Subcategories of Non-Polynomial Growth Tame Simply Connected Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 5 / 01 October 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1018-1043
- Print publication:
- 01 October 1996
-
- Article
-
- You have access
- Export citation