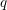Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Login Alert

Cancel

Log in

×

Register

Log In

(0) Cart

Back to search results

Home
Search

Search Results

Refine search

Access:

Only show content I have access to (0)

Content type:

Articles (3)

Author:

Publication date:

Over 3 years (3)

From year:

To year:

Apply From and To filters

Subject: Show more

Mathematics (1)

Actions for selected content:

Select all | Deselect all

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Search Title: required Please provide a title, maximum of 40 characters.

Cancel

×

3 results

Block–Göttsche invariants from wall-crossing
Part of
- Projective and enumerative geometry
- Representation theory of rings and algebras
S. A. Filippini, J. Stoppa
Journal:

Compositio Mathematica / Volume 151 / Issue 8 / August 2015

Published online by Cambridge University Press:

12 March 2015, pp. 1543-1567

Print publication:

August 2015
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We show how some of the refined tropical counts of Block and Göttsche emerge from the wall-crossing formalism. This leads naturally to a definition of a class of putative $q$-deformed Gromov–Witten invariants. We prove that this coincides with another natural $q$-deformation, provided by a result of Reineke and Weist in the context of quiver representations, when the latter is well defined.

SINGULARITIES OF ORBIT CLOSURES IN MODULE VARIETIES AND CONES OVER RATIONAL NORMAL CURVES
GRZEGORZ ZWARA
Journal:

Journal of the London Mathematical Society / Volume 74 / Issue 3 / December 2006

Published online by Cambridge University Press:

04 January 2007, pp. 623-638

Print publication:

December 2006
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Let $N$ be a point of an orbit closure $\overline{{\mathcal O}}_M$ in a module variety such that its orbit ${\mathcal O}_N$ has codimension 2 in $\overline{{\mathcal O}}_M$. We show that under some additional conditions the pointed variety $(\overline{{\mathcal O}}_M,N)$ is smoothly equivalent to a cone over a rational normal curve.

ON THE AUSLANDER–REITEN PERIODICITY OF SELF-INJECTIVE ALGEBRAS
ZYGMUNT POGORZAŁY
Journal:

Bulletin of the London Mathematical Society / Volume 36 / Issue 2 / March 2004

Published online by Cambridge University Press:

02 February 2004, pp. 156-168

Print publication:

March 2004
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
This paper investigates how to relate the syzygy periodicity of a self-injective algebra $A$ to its Auslander–Reiten periodicity. Moreover, a characterization is provided of the Auslander–Reiten bounded $A$–$A$-bimodules that are periodic.

Recommend this

Email your librarian or administrator to recommend adding this to your organisation's collection.

Your name * Please enter your name

Your email address * Please enter a valid email address.

Who would you like to send this to *

Optional message

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

×

Our Site

Accessibility
Contact & Help
Legal Notices

Our Platforms

Cambridge Core
Cambridge Open Engage
Cambridge Higher Education

Our Products

Journals
Books
Elements
Textbooks
Courseware

Join us online

Location

Please choose a valid location.

Rights & Permissions
Copyright
Privacy Notice
Terms of Use
Cookies Policy

Cambridge University Press 2025

Cancel

Confirm

×

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

3 results

Block–Göttsche invariants from wall-crossing

SINGULARITIES OF ORBIT CLOSURES IN MODULE VARIETIES AND CONES OVER RATIONAL NORMAL CURVES

ON THE AUSLANDER–REITEN PERIODICITY OF SELF-INJECTIVE ALGEBRAS