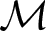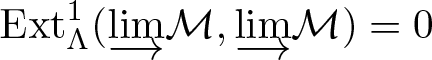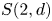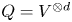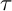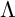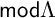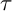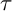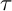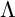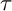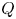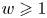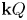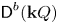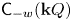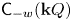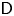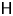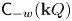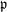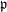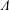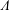Refine search
Actions for selected content:
49 results
FISHING FOR COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 07 July 2025, e5
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The rigidity of filtered colimits of n-cluster tilting subcategories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-14
-
- Article
- Export citation
Tachikawa's second conjecture, derived recollements, and gendo-symmetric algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 27 December 2024, pp. 2704-2737
- Print publication:
- November 2024
-
- Article
- Export citation
Resolving dualities and applications to homological invariants
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1861-1889
- Print publication:
- December 2025
-
- Article
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mutating signed
 $\tau$-exceptional sequences
$\tau$-exceptional sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 716-729
- Print publication:
- September 2023
-
- Article
- Export citation
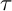 $\tau $-PERPENDICULAR WIDE SUBCATEGORIES
$\tau $-PERPENDICULAR WIDE SUBCATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 252 / December 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 959-984
- Print publication:
- December 2023
-
- Article
- Export citation
Derived categories of skew-gentle algebras and orbifolds
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 649-674
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functorially finite hearts, simple-minded systems in negative cluster categories, and noncrossing partitions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 23 February 2022, pp. 211-243
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterizations of right rejective chains
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 July 2021, pp. 557-570
- Print publication:
- September 2022
-
- Article
- Export citation
Representability and autoequivalence groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 08 February 2021, pp. 657-668
- Print publication:
- November 2021
-
- Article
- Export citation
GORENSTEIN SILTING COMPLEXES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 January 2021, pp. 122-135
- Print publication:
- January 2022
-
- Article
- Export citation
SPECIAL TILTING MODULES FOR ALGEBRAS WITH POSITIVE DOMINANT DIMENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 09 December 2020, pp. 79-105
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
COIDEMPOTENT SUBCOALGEBRAS AND SHORT EXACT SEQUENCES OF FINITARY 2-REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 19 March 2020, pp. 316-341
- Print publication:
- September 2021
-
- Article
- Export citation
Tropical friezes and the index in higher homological algebra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 23-49
- Print publication:
- July 2021
-
- Article
- Export citation
LOCAL DUALITY FOR THE SINGULARITY CATEGORY OF A FINITE DIMENSIONAL GORENSTEIN ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 1-24
- Print publication:
- December 2021
-
- Article
- Export citation
Coxeter Diagrams and the Köthe’s Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 656-686
- Print publication:
- June 2021
-
- Article
- Export citation
On Extensions for Gentle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 249-292
- Print publication:
- February 2021
-
- Article
- Export citation
Rigidity dimension of algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 26 November 2019, pp. 417-443
- Print publication:
- March 2021
-
- Article
- Export citation
n-T-COTORSION-FREE MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 297-311
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation