Refine search
Actions for selected content:
9 results
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation
Large-deviation asymptotics of condition numbers of random matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 1114-1130
- Print publication:
- December 2021
-
- Article
- Export citation
Convergence of an Anisotropic Perfectly Matched Layer Method for Helmholtz Scattering Problems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 358-382
- Print publication:
- August 2016
-
- Article
- Export citation
Submatrix Constrained Inverse Eigenvalue Problem involving Generalised Centrohermitian Matrices in Vibrating Structural Model Correction
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 42-59
- Print publication:
- February 2016
-
- Article
- Export citation
A FEM-Multigrid Scheme for Elliptic Nash-Equilibrium Multiobjective Optimal Control Problems
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 28 May 2015, pp. 253-282
- Print publication:
- May 2015
-
- Article
- Export citation
A Multilevel Method for the Solution of Time Dependent Optimal Transport
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 03 March 2015, pp. 97-111
- Print publication:
- February 2015
-
- Article
- Export citation
An Unpreconditioned Boundary-Integral for Iterative Solution of Scattering Problems with Non-Constant Leontovitch Impedance Boundary Conditions
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1431-1460
- Print publication:
- May 2014
-
- Article
- Export citation
Asymptotic Stability of an Eikonal Transformation Based ADI Method for the Paraxial Helmholtz Equation at High Wave Numbers
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1275-1292
- Print publication:
- October 2012
-
- Article
- Export citation
Truncated Newton-Based Multigrid Algorithm for Centroidal Voronoi Diagram Calculation
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 5 / Issue 2 / May 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 242-259
- Print publication:
- May 2012
-
- Article
- Export citation
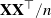
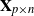
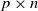
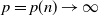
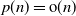
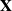
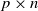
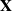
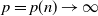
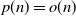
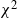
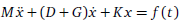 where
where 