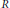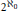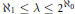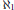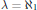Refine search
Actions for selected content:
5 results
ℵn-FREE MODULES OVER COMPLETE DISCRETE VALUATION DOMAINS WITH ALMOST TRIVIAL DUAL*
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 369-380
- Print publication:
- May 2013
-
- Article
-
- You have access
- Export citation
Almost-Free E-Rings of Cardinality ℵ1
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 4 / 01 August 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 750-765
- Print publication:
- 01 August 2003
-
- Article
-
- You have access
- Export citation
Ring Derivations on Function Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 1 / 01 March 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 69-72
- Print publication:
- 01 March 1990
-
- Article
-
- You have access
- Export citation
The Fixed Subring of Some Groups of Ring Automorphisms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 1 / 01 March 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-116
- Print publication:
- 01 March 1984
-
- Article
-
- You have access
- Export citation
Rings with Automorphisms Leaving no Nontrivial Proper Ideals Invariant
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 4 / 01 December 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-486
- Print publication:
- 01 December 1982
-
- Article
-
- You have access
- Export citation