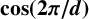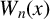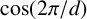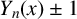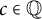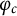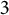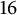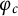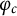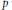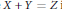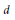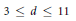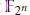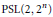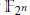Refine search
Actions for selected content:
10 results
FACTORING VARIANTS OF CHEBYSHEV POLYNOMIALS WITH MINIMAL POLYNOMIALS OF
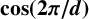 $\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
$\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 448-457
- Print publication:
- December 2022
-
- Article
- Export citation
Some results on the Flynn–Poonen–Schaefer conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 598-611
- Print publication:
- September 2022
-
- Article
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
Fraud risk assessment within blockchain transactions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 443-467
- Print publication:
- June 2019
-
- Article
- Export citation
Resultants of Chebyshev Polynomials: the First, Second, Third, and Fourth Kinds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 423-431
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Counting Decomposable Univariate Polynomials
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 05 September 2014, pp. 294-328
-
- Article
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
On Cauchy–Liouville–Mirimanoff Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 2 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 313-320
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation
PSL(2, 2n )-Extensions Over
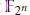
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 1 / 01 March 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-116
- Print publication:
- 01 March 2006
-
- Article
-
- You have access
- Export citation
Representation formulas for entire functions of exponential type and generalized bernoulli polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-316
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation