Refine search
Actions for selected content:
11 results
ON THE LARGEST PRIME DIVISOR OF n! + 1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTITATIVE GROWTH OF LINEAR RECURRENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-34
-
- Article
- Export citation
Linearly exponential checking is enough for the lonely runner conjecture and some of its variants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e164
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Möbius Randomness Law for Frobenius Traces of Ordinary Curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 192-203
- Print publication:
- March 2021
-
- Article
- Export citation
A LOWER BOUND FOR THE LARGE SIEVE WITH SQUARE MODULI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 225-229
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Numbers with Almost all Convergents in a Cantor Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 869-875
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 375-387
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 June 2015, pp. 79-100
- Print publication:
- 2016
-
- Article
- Export citation
ON THE DISTRIBUTION OF
 -FREE NUMBERS AND NON-VANISHING FOURIER COEFFICIENTS OF CUSP FORMS
-FREE NUMBERS AND NON-VANISHING FOURIER COEFFICIENTS OF CUSP FORMS
-
- Journal:
- Glasgow Mathematical Journal / Volume 54 / Issue 2 / May 2012
- Published online by Cambridge University Press:
- 29 March 2012, pp. 381-397
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
DISTANCE BETWEEN ARITHMETIC PROGRESSIONS AND PERFECT SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 41-49
- Print publication:
- January 2011
-
- Article
- Export citation
ON A PROBLEM OF BROCARD
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 4 / August 2005
- Published online by Cambridge University Press:
- 02 August 2005, pp. 502-506
- Print publication:
- August 2005
-
- Article
- Export citation


















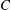
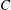
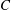
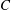
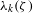
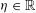
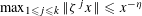


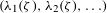
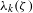
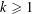
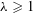
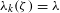
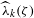
 -FREE NUMBERS AND NON-VANISHING FOURIER COEFFICIENTS OF CUSP FORMS
-FREE NUMBERS AND NON-VANISHING FOURIER COEFFICIENTS OF CUSP FORMS