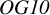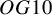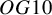Refine search
Actions for selected content:
5 results
Unimodular Hunting II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite groups of symplectic birational transformations of IHS manifolds of
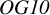 $\mathit {OG10}$ type
$\mathit {OG10}$ type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite symplectic actions on the K3 lattice
-
- Journal:
- Nagoya Mathematical Journal / Volume 206 / June 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 99-153
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
The Ample Cone for a K3 Surface
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 3 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-499
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation