We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We investigate computability theoretic and descriptive set theoretic contents of various kinds of analytic choice principles by performing a detailed analysis of the Medvedev lattice of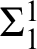 
$\Sigma ^1_1$
-closed sets. Among others, we solve an open problem on the Weihrauch degree of the parallelization of the 
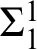$\Sigma ^1_1$
-choice principle on the integers. Harrington’s unpublished result on a jump hierarchy along a pseudo-well-ordering plays a key role in solving this problem.
