Published online by Cambridge University Press: 03 December 2020
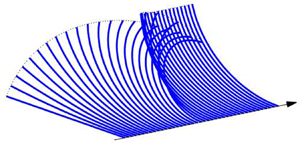
A reduced model is presented for the dynamics of a slender sheet of a viscoelastic fluid. Starting with the Oldroyd-B constitutive model and exploiting an asymptotic analysis in the small aspect ratio of the sheet, equations are derived for the evolution of a ‘visco-elastica’. These depend on an elastic modulus, a creep viscosity and a solvent viscosity. They resemble standard equations for an elastica or a viscida, to which they reduce under the appropriate limits. The model is used to explore the effects of viscoelasticity on the dynamics of a curling ribbon, a drooping cantilever, buckling sheets, snap-through and a falling catenary. We then incorporate a yield stress, for a fluid that deforms by creep only above a critical stress, revisiting the curling and cantilever problems. This model generalises a number of previous theories for viscoelastic and viscoplastic ribbons.