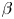1 Introduction
Quasisymmetry, along with quasi-isodynamicity, is one of the two main approaches to confining particle orbits inside a stellarator (Boozer Reference Boozer1998; Helander Reference Helander2014). Quasisymmetry is usually defined as a stellarator configuration where the magnitude of the magnetic field satisfies $|\boldsymbol {B}| = B(\psi, M\theta - N\phi )$![]() for some integers $M,N$
for some integers $M,N$![]() , where $(\psi,\theta,\phi )$
, where $(\psi,\theta,\phi )$![]() is a straight field line coordinate system (Helander Reference Helander2014). Thus, the magnetic field magnitude is two-dimensional, but the full vector can still be three-dimensional. Such a device can be modelled using the near-axis expansion (Garren & Boozer Reference Garren and Boozer1991a,Reference Garren and Boozerb; Landreman & Sengupta Reference Landreman and Sengupta2018), which consists of Taylor-expanding all quantities of interest in either the distance from the magnetic axis (direct coordinates) or the square root of toroidal flux (inverse coordinates) (Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020), and balancing the coefficients in the magnetohydrodynamics (MHD) equilibrium equations at each order in the Taylor expansion, resulting in a system of coupled ordinary differential and algebraic equations. However, the imposition of the quasisymmetry constraint, in addition to force balance, results in the system being overconstrained at all orders beyond the first in the near-axis expansion (Garren & Boozer Reference Garren and Boozer1991a). At second order, this can be rectified by not imposing quasisymmetry directly, but rather optimizing for it. Unlike traditional optimization, second-order near-axis optimization is much faster due to the significantly reduced parameter space (Landreman Reference Landreman2022). Beyond second order, there is evidence that the Taylor series of the near-axis model begins to diverge (Rodriguez Reference Rodriguez2022).
is a straight field line coordinate system (Helander Reference Helander2014). Thus, the magnetic field magnitude is two-dimensional, but the full vector can still be three-dimensional. Such a device can be modelled using the near-axis expansion (Garren & Boozer Reference Garren and Boozer1991a,Reference Garren and Boozerb; Landreman & Sengupta Reference Landreman and Sengupta2018), which consists of Taylor-expanding all quantities of interest in either the distance from the magnetic axis (direct coordinates) or the square root of toroidal flux (inverse coordinates) (Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020), and balancing the coefficients in the magnetohydrodynamics (MHD) equilibrium equations at each order in the Taylor expansion, resulting in a system of coupled ordinary differential and algebraic equations. However, the imposition of the quasisymmetry constraint, in addition to force balance, results in the system being overconstrained at all orders beyond the first in the near-axis expansion (Garren & Boozer Reference Garren and Boozer1991a). At second order, this can be rectified by not imposing quasisymmetry directly, but rather optimizing for it. Unlike traditional optimization, second-order near-axis optimization is much faster due to the significantly reduced parameter space (Landreman Reference Landreman2022). Beyond second order, there is evidence that the Taylor series of the near-axis model begins to diverge (Rodriguez Reference Rodriguez2022).
Magnetic shear appears at third order in the near-axis expansion, and thus depends on third-order quantities. While, in some cases, setting the third-order quantities to zero and evaluating the shear based on just lower-order quantities provides a reasonable estimate, in other cases, such an approach produces large deviations from the shear calculated in numerical solutions (Rodriguez Reference Rodriguez2022). This presents a challenge for the modelling of quasisymmetric devices, as shear is an important quantity that affects ballooning stability of equilibria, among other things (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978).
A complementary model for quasiaxisymmetric stellarators near axisymmetry that can incorporate shear has been derived in a previous paper (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a). In this paper, we propose a more general model that is applicable to both quasiaxisymmetric and quasi-helically symmetric stellarators far from axisymmetry. In both cases, the difficulties related to shear are avoided by not using Taylor expansions like the near-axis model does. Instead, we perform an asymptotic expansion around a vacuum magnetic field $\boldsymbol {\nabla }\chi$![]() , where $\chi$
, where $\chi$![]() is the magnetic scalar potential. The dominance of the vacuum field is a natural assumption, given the design principles of stellarators, which aim to confine the plasma without having a large plasma current (Freidberg Reference Freidberg2014). Our approach is inspired by Strauss’ derivation of reduced MHD (Strauss Reference Strauss1997), who also expanded around a vacuum field, with the main difference being that Strauss assumes $p = O(\epsilon ^2)$
is the magnetic scalar potential. The dominance of the vacuum field is a natural assumption, given the design principles of stellarators, which aim to confine the plasma without having a large plasma current (Freidberg Reference Freidberg2014). Our approach is inspired by Strauss’ derivation of reduced MHD (Strauss Reference Strauss1997), who also expanded around a vacuum field, with the main difference being that Strauss assumes $p = O(\epsilon ^2)$![]() , whereas we allow for a higher $\beta$
, whereas we allow for a higher $\beta$![]() with $p = O(\epsilon )$
with $p = O(\epsilon )$![]() , where $\epsilon$
, where $\epsilon$![]() is a small parameter. We will show that such an ordering requires $\chi$
is a small parameter. We will show that such an ordering requires $\chi$![]() to have a specific form. In the limit of low $\beta$
to have a specific form. In the limit of low $\beta$![]() , our model will reduce to the equilibrium limit of Strauss’ equations under the assumption of quasisymmetry with our choice of $\chi$
, our model will reduce to the equilibrium limit of Strauss’ equations under the assumption of quasisymmetry with our choice of $\chi$![]() . The derivation will closely follow that of the Freidberg high-$\beta$
. The derivation will closely follow that of the Freidberg high-$\beta$![]() stellarator model (Freidberg Reference Freidberg2014), except that Freidberg expands around a purely toroidal field $B_0\hat {\phi }$
stellarator model (Freidberg Reference Freidberg2014), except that Freidberg expands around a purely toroidal field $B_0\hat {\phi }$![]() , whereas we allow for a more general zeroth-order field. Once the model is derived, we will present several solutions and a numerical validation of one of those solutions.
, whereas we allow for a more general zeroth-order field. Once the model is derived, we will present several solutions and a numerical validation of one of those solutions.
2 Derivation
To begin, we expand the magnetic field around a vacuum magnetic field $\boldsymbol {\nabla }\chi$![]() , where $\nabla ^2\chi = O(\epsilon ^2)$
, where $\nabla ^2\chi = O(\epsilon ^2)$![]() :
:
We will order relative to the $\boldsymbol {\nabla }\chi$![]() term: $B_v = |\boldsymbol {\nabla }\chi | = O(1)$
term: $B_v = |\boldsymbol {\nabla }\chi | = O(1)$![]() , $B_1 = O(\epsilon )$
, $B_1 = O(\epsilon )$![]() and $\boldsymbol {B}_{\perp 1} = O(\epsilon )$
and $\boldsymbol {B}_{\perp 1} = O(\epsilon )$![]() , where $\epsilon = \max |\boldsymbol {B} - \boldsymbol {\nabla }\chi |/B_v \ll 1$
, where $\epsilon = \max |\boldsymbol {B} - \boldsymbol {\nabla }\chi |/B_v \ll 1$![]() and $\boldsymbol {B}_{\perp 1}\perp \boldsymbol {\nabla }\chi$
and $\boldsymbol {B}_{\perp 1}\perp \boldsymbol {\nabla }\chi$![]() . In addition, the derivative along the vacuum field must be ordered as $\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(\epsilon )$
. In addition, the derivative along the vacuum field must be ordered as $\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(\epsilon )$![]() , whereas $\boldsymbol {\nabla }_\perp = \boldsymbol {\nabla } - B_v^{-2}\boldsymbol {\nabla }\chi\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(1)$
, whereas $\boldsymbol {\nabla }_\perp = \boldsymbol {\nabla } - B_v^{-2}\boldsymbol {\nabla }\chi\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(1)$![]() . The derivative ordering can be justified as follows. The the perpendicular length scale will be $\sim r_0$
. The derivative ordering can be justified as follows. The the perpendicular length scale will be $\sim r_0$![]() , whereas the length scale along $\boldsymbol {\nabla }\chi$
, whereas the length scale along $\boldsymbol {\nabla }\chi$![]() will be $\sim 2{\rm \pi} R_0$
will be $\sim 2{\rm \pi} R_0$![]() , where $r_0$
, where $r_0$![]() and $R_0$
and $R_0$![]() are the minor and major radii, respectively. Thus, the ratio of the length scales must be less than $1/2{\rm \pi}$
are the minor and major radii, respectively. Thus, the ratio of the length scales must be less than $1/2{\rm \pi}$![]() , and no more than 0.1 for any realistic aspect ratio.
, and no more than 0.1 for any realistic aspect ratio.
Taking the divergence of (2.1), we have $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B} = \boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla }(B_1/B_v) + \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {B}_{\perp 1} = {\boldsymbol {\nabla }_\perp \boldsymbol {\cdot }\boldsymbol {B}_{\perp 1}} + O(\epsilon ^2)$![]() . Since $\boldsymbol {\nabla }_\perp$
. Since $\boldsymbol {\nabla }_\perp$![]() is two-dimensional, a stream function $A = O(\epsilon )$
is two-dimensional, a stream function $A = O(\epsilon )$![]() can be introduced: $\boldsymbol {B}_{\perp 1} = \boldsymbol {\nabla } A\times \boldsymbol {\nabla }\chi$
can be introduced: $\boldsymbol {B}_{\perp 1} = \boldsymbol {\nabla } A\times \boldsymbol {\nabla }\chi$![]() . Note that Strauss uses the symbol $\psi$
. Note that Strauss uses the symbol $\psi$![]() for his stream function, but we will use $A$
for his stream function, but we will use $A$![]() instead to avoid confusion with the flux surface label.
instead to avoid confusion with the flux surface label.
Following Strauss, we can write the current density as follows:
where $\varDelta ^* = B_v^{-2}\boldsymbol {\nabla }\boldsymbol {\cdot }(B_v^2\boldsymbol {\nabla }_\perp )$![]() , as defined by Strauss (Reference Strauss1997), and the expression for $j_\parallel$
, as defined by Strauss (Reference Strauss1997), and the expression for $j_\parallel$![]() is easily obtained by dotting the curl of (2.1) with $\boldsymbol {\nabla }\chi$
is easily obtained by dotting the curl of (2.1) with $\boldsymbol {\nabla }\chi$![]() and using the identity $\boldsymbol {\nabla } f\boldsymbol {\cdot }\boldsymbol {\nabla }\times \boldsymbol {U} = -\boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\nabla } f\times \boldsymbol {U})$
and using the identity $\boldsymbol {\nabla } f\boldsymbol {\cdot }\boldsymbol {\nabla }\times \boldsymbol {U} = -\boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {\nabla } f\times \boldsymbol {U})$![]() . An alternate expression can be obtained by taking the curl of (2.1):
. An alternate expression can be obtained by taking the curl of (2.1):
The last two terms are both $O(\epsilon ^2)$![]() . This becomes more obvious for the last term if we write it as $(\boldsymbol {\nabla } A\boldsymbol {\cdot }\boldsymbol {\nabla })\boldsymbol {\nabla }\chi = \boldsymbol {\nabla }(\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } A) - (\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla })\boldsymbol {\nabla } A$
. This becomes more obvious for the last term if we write it as $(\boldsymbol {\nabla } A\boldsymbol {\cdot }\boldsymbol {\nabla })\boldsymbol {\nabla }\chi = \boldsymbol {\nabla }(\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } A) - (\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla })\boldsymbol {\nabla } A$![]() . Equating the perpendicular components of the current at lowest order, we obtain
. Equating the perpendicular components of the current at lowest order, we obtain
Unless the second term is a gradient, both terms are linearly independent and must be individually zero at order $\epsilon$![]() (see Appendix A for details). If the second term is a gradient, we must have either $B_v = B_v(p)$
(see Appendix A for details). If the second term is a gradient, we must have either $B_v = B_v(p)$![]() or $B_v = B_0 + O(\epsilon )$
or $B_v = B_0 + O(\epsilon )$![]() where $B_0 = \mathrm {const}$
where $B_0 = \mathrm {const}$![]() ; however, the former cannot be true as $|\boldsymbol {B}|$
; however, the former cannot be true as $|\boldsymbol {B}|$![]() can only be a flux function in axisymmetry (Schief Reference Schief2003), and since $|\boldsymbol {B}| = B_v + O(\epsilon ^2)$
can only be a flux function in axisymmetry (Schief Reference Schief2003), and since $|\boldsymbol {B}| = B_v + O(\epsilon ^2)$![]() , $B_v$
, $B_v$![]() cannot be a flux function either. Thus, to satisfy the equation, we must either ensure that both terms are individually zero, i.e. $p = O(\epsilon ^2)$
cannot be a flux function either. Thus, to satisfy the equation, we must either ensure that both terms are individually zero, i.e. $p = O(\epsilon ^2)$![]() and $B_1 = 0$
and $B_1 = 0$![]() , or let $B_v = B_0 + O(\epsilon )$
, or let $B_v = B_0 + O(\epsilon )$![]() . The former corresponds to the equilibrium limit of the Strauss equations, and so we focus on the latter. The equation then yields:
. The former corresponds to the equilibrium limit of the Strauss equations, and so we focus on the latter. The equation then yields:
This is simply the lowest-order radial pressure balance condition; similar expressions appear in most reduced MHD models that assume $p = O(\epsilon )$![]() (Freidberg Reference Freidberg2014; Zocco, Helander & Weitzner Reference Zocco, Helander and Weitzner2020; Kruger, Hegna & Callen Reference Kruger, Hegna and Callen1998). Taking the divergence of (2.2) then gives the generalized version of Strauss’ (26) in the equilibrium limit:
(Freidberg Reference Freidberg2014; Zocco, Helander & Weitzner Reference Zocco, Helander and Weitzner2020; Kruger, Hegna & Callen Reference Kruger, Hegna and Callen1998). Taking the divergence of (2.2) then gives the generalized version of Strauss’ (26) in the equilibrium limit:
The only other equation of Strauss’ reduced MHD that is non-trivial in the equilibrium limit can be written simply as $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } p = 0$![]() .
.
Equation (2.6) can be further simplified by exploiting the two-term quasisymmetry condition, the imposition of which is equivalent to demanding that $|\boldsymbol {B}| = B(\psi, M\theta - N\phi )$![]() (Helander Reference Helander2014): $(\boldsymbol {B}\times \boldsymbol {\nabla }\psi )\boldsymbol {\cdot }\boldsymbol {\nabla } B = F(\psi )\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } B$
(Helander Reference Helander2014): $(\boldsymbol {B}\times \boldsymbol {\nabla }\psi )\boldsymbol {\cdot }\boldsymbol {\nabla } B = F(\psi )\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } B$![]() , where $\psi$
, where $\psi$![]() is the toroidal flux. Applying the ordering, this condition can be written in one of two equivalent ways:
is the toroidal flux. Applying the ordering, this condition can be written in one of two equivalent ways:
where an alternate flux surface label $\varPsi = \int d\psi /F(\psi )$![]() is defined to absorb the $F(\psi )$
is defined to absorb the $F(\psi )$![]() factor. Note that $F(\psi )$
factor. Note that $F(\psi )$![]() is $O(\epsilon ^{-1})$
is $O(\epsilon ^{-1})$![]() (Helander Reference Helander2014), so $\varPsi = O(\epsilon )$
(Helander Reference Helander2014), so $\varPsi = O(\epsilon )$![]() . Using (2.7a), the second term in (2.6) can be rewritten as $p'(\boldsymbol {\nabla }\chi \times \boldsymbol {\nabla }\varPsi )\boldsymbol {\cdot }\boldsymbol {\nabla } B_v^{-2} = p'\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } B_v^{-2}$
. Using (2.7a), the second term in (2.6) can be rewritten as $p'(\boldsymbol {\nabla }\chi \times \boldsymbol {\nabla }\varPsi )\boldsymbol {\cdot }\boldsymbol {\nabla } B_v^{-2} = p'\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } B_v^{-2}$![]() , which results in both terms in the equation having $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$
, which results in both terms in the equation having $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() acting on something. Since $p'$
acting on something. Since $p'$![]() commutes with $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$
commutes with $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() , we can remove the $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$
, we can remove the $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() operator, obtaining a Grad–Shafranov-like equation:
operator, obtaining a Grad–Shafranov-like equation:
where $H$![]() and $\mu _0 p'/B_0^2$
and $\mu _0 p'/B_0^2$![]() are functions of $\varPsi$
are functions of $\varPsi$![]() that appear due to the integration. Although $H$
that appear due to the integration. Although $H$![]() is arbitrary, the $B_0$
is arbitrary, the $B_0$![]() term cannot be absorbed into it as it is necessary to cancel the $O(1)$
term cannot be absorbed into it as it is necessary to cancel the $O(1)$![]() part of $1/B_v^2$
part of $1/B_v^2$![]() so that all terms are of the same order. Further, note that $H$
so that all terms are of the same order. Further, note that $H$![]() is a degree of freedom that allows us to specify the toroidal current profile; its axisymmetric equivalent is the $FF'$
is a degree of freedom that allows us to specify the toroidal current profile; its axisymmetric equivalent is the $FF'$![]() term in the standard Grad–Shafranov equation.
term in the standard Grad–Shafranov equation.
To make further progress, $\chi$![]() has to be specified explicitly. The constraint $B_v = B_0 + O(\epsilon )$
has to be specified explicitly. The constraint $B_v = B_0 + O(\epsilon )$![]() , which, as we have seen, arises from the high-$\beta$
, which, as we have seen, arises from the high-$\beta$![]() assumption, requires that $\chi = B_0 l$
assumption, requires that $\chi = B_0 l$![]() . This can be seen by writing $B_v^2$
. This can be seen by writing $B_v^2$![]() in orthogonal Mercier coordinates $(\rho,\omega,l)$
in orthogonal Mercier coordinates $(\rho,\omega,l)$![]() aligned to a magnetic axis with curvature $\kappa$
aligned to a magnetic axis with curvature $\kappa$![]() and torsion $\tau$
and torsion $\tau$![]() (Solov'ev & Shafranov Reference Solov'ev and Shafranov1970; Jorge et al. Reference Jorge, Sengupta and Landreman2020):
(Solov'ev & Shafranov Reference Solov'ev and Shafranov1970; Jorge et al. Reference Jorge, Sengupta and Landreman2020):
where $h = 1 - \kappa \rho \cos \theta$![]() , $\theta = \omega - \int _0^l\tau dl$
, $\theta = \omega - \int _0^l\tau dl$![]() . On the axis, we must have $\partial \chi /\partial \rho |_{\rho =0} = \lim _{\rho \to 0}\rho ^{-1}\partial \chi /\partial \omega = 0$
. On the axis, we must have $\partial \chi /\partial \rho |_{\rho =0} = \lim _{\rho \to 0}\rho ^{-1}\partial \chi /\partial \omega = 0$![]() , since the axis is a field line. Thus, the constant $B_0^2$
, since the axis is a field line. Thus, the constant $B_0^2$![]() can only come from the last term. It then follows that $\kappa \rho = O(\epsilon )$
can only come from the last term. It then follows that $\kappa \rho = O(\epsilon )$![]() , so that $1/h^2 = 1 + O(\epsilon )$
, so that $1/h^2 = 1 + O(\epsilon )$![]() ; otherwise, $\chi$
; otherwise, $\chi$![]() would have depended on $\rho$
would have depended on $\rho$![]() and $\omega$
and $\omega$![]() at the lowest order, which is a contradiction. With that in mind, we can integrate at the zeroth order, obtaining $\chi = B_0 l + O(\epsilon )$
at the lowest order, which is a contradiction. With that in mind, we can integrate at the zeroth order, obtaining $\chi = B_0 l + O(\epsilon )$![]() . We can ignore the $O(\epsilon )$
. We can ignore the $O(\epsilon )$![]() correction to $\chi$
correction to $\chi$![]() without loss of generality; as will be shown at the end of the section, it can be absorbed into the $\boldsymbol {\nabla } A\times \boldsymbol {\nabla }\chi$
without loss of generality; as will be shown at the end of the section, it can be absorbed into the $\boldsymbol {\nabla } A\times \boldsymbol {\nabla }\chi$![]() term. Note that we can now give $\epsilon$
term. Note that we can now give $\epsilon$![]() a more intuitive meaning: given that $\rho \sim r_0$
a more intuitive meaning: given that $\rho \sim r_0$![]() and $\kappa,\tau \sim 1/R_0$
and $\kappa,\tau \sim 1/R_0$![]() , we should order $r_0 = O(1)$
, we should order $r_0 = O(1)$![]() and $R_0 = O(\epsilon )$
and $R_0 = O(\epsilon )$![]() , and hence we have a large aspect ratio expansion with $\epsilon$
, and hence we have a large aspect ratio expansion with $\epsilon$![]() acting as the inverse aspect ratio. Finally, it should be emphasized that the only arbitrary assumption made in this derivation is that $p = O(\epsilon )$
acting as the inverse aspect ratio. Finally, it should be emphasized that the only arbitrary assumption made in this derivation is that $p = O(\epsilon )$![]() . The rest of the ordering, while not rigorous, is still justified by heuristic arguments.
. The rest of the ordering, while not rigorous, is still justified by heuristic arguments.
As a sanity check, we will demonstrate that $\chi = B_0 l$![]() only breaks the divergence-free condition at second order, which is acceptable, since this is a first-order model. Using the Laplace operator in orthogonal Mercier coordinates (see (3.4) of Sengupta et al. (Reference Sengupta, Rodriguez, Jorge, Landreman and Bhattacharjee2024b)), we have
only breaks the divergence-free condition at second order, which is acceptable, since this is a first-order model. Using the Laplace operator in orthogonal Mercier coordinates (see (3.4) of Sengupta et al. (Reference Sengupta, Rodriguez, Jorge, Landreman and Bhattacharjee2024b)), we have
since $h = 1 + O(\epsilon )$![]() and $\partial /\partial l = B_0^{-1}h^2\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(\epsilon )$
and $\partial /\partial l = B_0^{-1}h^2\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(\epsilon )$![]() .
.
Throughout the rest of the paper, we will use non-orthogonal Mercier coordinates $(x,y,l)$![]() , where $x = \rho \cos \theta$
, where $x = \rho \cos \theta$![]() and $y = \rho \sin \theta$
and $y = \rho \sin \theta$![]() . The metric tensor is as follows (Solov'ev & Shafranov Reference Solov'ev and Shafranov1970):
. The metric tensor is as follows (Solov'ev & Shafranov Reference Solov'ev and Shafranov1970):

Using the metric tensor and $\chi = B_0 l$![]() , which implies $B_v = B_0/h$
, which implies $B_v = B_0/h$![]() , (2.7b) can be written as
, (2.7b) can be written as
The non-orthogonal Mercier coordinates have simplified the equation such that it can now be integrated:
where $a$![]() is an arbitrary function. This allows us to write (2.8) as an equation for $\varPsi$
is an arbitrary function. This allows us to write (2.8) as an equation for $\varPsi$![]() :
:
where we have used $B_v = B_0|\boldsymbol {\nabla } l| = B_0/(1 - \kappa x)$![]() and $\varDelta ^* = \varDelta _\perp + O(\epsilon )$
and $\varDelta ^* = \varDelta _\perp + O(\epsilon )$![]() , and dropped terms of order $\epsilon ^2$
, and dropped terms of order $\epsilon ^2$![]() and higher.
and higher.
Although we now have an equation for $\varPsi$![]() , solving it is non-trivial, as $\varPsi$
, solving it is non-trivial, as $\varPsi$![]() is overconstrained, due to also having to satisfy the equation $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$
is overconstrained, due to also having to satisfy the equation $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$![]() , which, after inserting $A$
, which, after inserting $A$![]() from (2.13), can be written in Mercier coordinates as
from (2.13), can be written in Mercier coordinates as
where we have inserted the expression for $A$![]() from (2.13). The characteristics of this equation are given by
from (2.13). The characteristics of this equation are given by

For $\varPsi$![]() to satisfy (2.15), it must be a function of only $C_1$
to satisfy (2.15), it must be a function of only $C_1$![]() and $C_2$
and $C_2$![]() , as defined in (2.16a,b). One must then ensure that the function also satisfies (2.14) at all values of $l$
, as defined in (2.16a,b). One must then ensure that the function also satisfies (2.14) at all values of $l$![]() .
.
Having derived the model, we now show that adding an $O(\epsilon )$![]() correction to $\chi$
correction to $\chi$![]() will not change it. Thus, if the assumption that the $B_0 l$
will not change it. Thus, if the assumption that the $B_0 l$![]() is the dominant term in $\chi$
is the dominant term in $\chi$![]() holds, the model is fully general. Indeed, suppose that we add a correction $\chi _1 = O(\epsilon )$
holds, the model is fully general. Indeed, suppose that we add a correction $\chi _1 = O(\epsilon )$![]() to $\chi$
to $\chi$![]() , then at order $\epsilon$
, then at order $\epsilon$![]() , this term can be absorbed into the $\boldsymbol {\nabla } A\times \boldsymbol {\nabla }\chi$
, this term can be absorbed into the $\boldsymbol {\nabla } A\times \boldsymbol {\nabla }\chi$![]() term by replacing $A\mapsto A + \tilde {A}$
term by replacing $A\mapsto A + \tilde {A}$![]() , where $\boldsymbol {\nabla }\chi _1 = B_0\boldsymbol {\nabla }\tilde {A}\times \boldsymbol {\nabla } l$
, where $\boldsymbol {\nabla }\chi _1 = B_0\boldsymbol {\nabla }\tilde {A}\times \boldsymbol {\nabla } l$![]() . The fact that such an $\tilde {A}$
. The fact that such an $\tilde {A}$![]() exists can be seen by writing out the contravariant $x$
exists can be seen by writing out the contravariant $x$![]() and $y$
and $y$![]() components of this relation:
components of this relation:
These are just the Cauchy–Riemann equations; since $\chi _1$![]() must satisfy the Laplace equation at order $\epsilon$
must satisfy the Laplace equation at order $\epsilon$![]() , a corresponding $\tilde {A}$
, a corresponding $\tilde {A}$![]() is guaranteed to exist.
is guaranteed to exist.
3 Consistency with the first-order near-axis model
The simplest ansatz for $\varPsi$![]() that will work in this model is a quadratic polynomial in $C_1$
that will work in this model is a quadratic polynomial in $C_1$![]() and $C_2$
and $C_2$![]() , which are defined in (2.16a,b):
, which are defined in (2.16a,b):

where $\varLambda = \int \kappa ^{-2}(\tau + a_2)\,{\rm d} l$![]() ; and $a$
; and $a$![]() was chosen as $a = a_2(l)x^2/2$
was chosen as $a = a_2(l)x^2/2$![]() . This represents a plasma with an elliptic cross-section that rotates about the magnetic axis as $l$
. This represents a plasma with an elliptic cross-section that rotates about the magnetic axis as $l$![]() varies. Inserting this expression into the Grad–Shafranov equation (2.14), we obtain an equation expressing $a_2$
varies. Inserting this expression into the Grad–Shafranov equation (2.14), we obtain an equation expressing $a_2$![]() in terms of $\varLambda$
in terms of $\varLambda$![]() . Note that, when inserting (3.1) into the Grad–Shafranov equation, all terms on the left-hand side of (2.14) will depend only on $l$
. Note that, when inserting (3.1) into the Grad–Shafranov equation, all terms on the left-hand side of (2.14) will depend only on $l$![]() , whereas terms on the right-hand side can depend on all three variables. Thus, we further assume $p = O(\epsilon ^2)$
, whereas terms on the right-hand side can depend on all three variables. Thus, we further assume $p = O(\epsilon ^2)$![]() and $H(\varPsi ) = H_0 = \mathrm {const}$
and $H(\varPsi ) = H_0 = \mathrm {const}$![]() ; this is consistent with the near-axis model, where pressure enters only at the second order. Proceeding, we have
; this is consistent with the near-axis model, where pressure enters only at the second order. Proceeding, we have
Finally, we can combine ${\rm d}\varLambda /{\rm d} l = (\tau + a_2)/\kappa ^2$![]() , which follows from the definition of $\varLambda$
, which follows from the definition of $\varLambda$![]() , with the above equation, resulting in a Riccati equation for $\varLambda$
, with the above equation, resulting in a Riccati equation for $\varLambda$![]() :
:
The last step is to enforce periodicity on $\varLambda$![]() . Averaging the above equation over $l$
. Averaging the above equation over $l$![]() removes the derivative term, resulting in the following constraint:
removes the derivative term, resulting in the following constraint:
where $\langle f(l)\rangle = L^{-1}\int _0^L f(l)\mathrm {d}l$![]() , with $L$
, with $L$![]() being the axis length. Thus, only two of the $s_i$
being the axis length. Thus, only two of the $s_i$![]() constants are free, with the remaining one determined by the above constraint. In practice, since $\varLambda$
constants are free, with the remaining one determined by the above constraint. In practice, since $\varLambda$![]() is not known a priori, (3.3) and (3.4) must be solved iteratively: first, one makes an initial guess for the unknown $s_i$
is not known a priori, (3.3) and (3.4) must be solved iteratively: first, one makes an initial guess for the unknown $s_i$![]() , then (3.3) is solved for $\varLambda$
, then (3.3) is solved for $\varLambda$![]() , which allows one to calculate the corrected value of the unknown $s_i$
, which allows one to calculate the corrected value of the unknown $s_i$![]() from (3.4); this cycle is repeated until convergence is achieved. This same method is used in the near-axis model to solve the $\sigma$
from (3.4); this cycle is repeated until convergence is achieved. This same method is used in the near-axis model to solve the $\sigma$![]() -equation while simultaneously finding the correct rotational transform that is compatible with periodicity (Landreman, Sengupta & Plunk Reference Landreman, Sengupta and Plunk2019).
-equation while simultaneously finding the correct rotational transform that is compatible with periodicity (Landreman, Sengupta & Plunk Reference Landreman, Sengupta and Plunk2019).
Now consider the lowest order near-axis expression for $\varPsi$![]() (Jorge et al. Reference Jorge, Sengupta and Landreman2020):
(Jorge et al. Reference Jorge, Sengupta and Landreman2020):

where $x = \rho \cos \theta$![]() , $y = \rho \sin \theta$
, $y = \rho \sin \theta$![]() , $F_0$
, $F_0$![]() is the value of $F(\psi )$
is the value of $F(\psi )$![]() on axis and $\eta$
on axis and $\eta$![]() and $\delta$
and $\delta$![]() are functions of $l$
are functions of $l$![]() . Note that $F_0$
. Note that $F_0$![]() , as defined here, is the inverse of the $F_0$
, as defined here, is the inverse of the $F_0$![]() of Jorge et al. (Reference Jorge, Sengupta and Landreman2020). In quasisymmetry, we have $\cosh \eta - \sinh \eta \cos 2\delta = \bar {\eta }^2/\kappa ^2$
of Jorge et al. (Reference Jorge, Sengupta and Landreman2020). In quasisymmetry, we have $\cosh \eta - \sinh \eta \cos 2\delta = \bar {\eta }^2/\kappa ^2$![]() (Jorge et al. Reference Jorge, Sengupta and Landreman2020). Since $\bar {\eta } = \mathrm {const}$
(Jorge et al. Reference Jorge, Sengupta and Landreman2020). Since $\bar {\eta } = \mathrm {const}$![]() Footnote 1 , the $y^2$
Footnote 1 , the $y^2$![]() term of (3.1) agrees with that of (3.5) and $s_3 = {\rm \pi}B_0\bar {\eta }^2/F_0$
term of (3.1) agrees with that of (3.5) and $s_3 = {\rm \pi}B_0\bar {\eta }^2/F_0$![]() . Further, taking $4(\text {coef. of }x^2)(\text {coef. of }y^2) - (\text {coef. of } xy)^2$
. Further, taking $4(\text {coef. of }x^2)(\text {coef. of }y^2) - (\text {coef. of } xy)^2$![]() from (3.5), we see that the $l$
from (3.5), we see that the $l$![]() -dependent terms cancel and we are left with just a constant, $4{\rm \pi} ^2 B_0^2/F_0^2$
-dependent terms cancel and we are left with just a constant, $4{\rm \pi} ^2 B_0^2/F_0^2$![]() . Likewise, when using the corresponding coefficients from (3.1), the terms with $\varLambda$
. Likewise, when using the corresponding coefficients from (3.1), the terms with $\varLambda$![]() cancel and we get $4s_1 s_3 - s_2^2 = 4{\rm \pi} ^2 B_0^2/F_0^2$
cancel and we get $4s_1 s_3 - s_2^2 = 4{\rm \pi} ^2 B_0^2/F_0^2$![]() .
.
Next, we show that (3.3) is equivalent to the $\sigma$![]() -equation of Jorge et al. (Reference Jorge, Sengupta and Landreman2020). A relation between $\varLambda$
-equation of Jorge et al. (Reference Jorge, Sengupta and Landreman2020). A relation between $\varLambda$![]() and $\sigma$
and $\sigma$![]() can be obtained by comparing the coefficients of $xy$
can be obtained by comparing the coefficients of $xy$![]() in (3.1) and (3.5). Since $\sigma = \sinh \eta \sin 2\delta$
in (3.1) and (3.5). Since $\sigma = \sinh \eta \sin 2\delta$![]() (Jorge et al. Reference Jorge, Sengupta and Landreman2020), we have
(Jorge et al. Reference Jorge, Sengupta and Landreman2020), we have
Inserting this into (3.3) and replacing the $s_i$![]() variables with near-axis variables, we get
variables with near-axis variables, we get
In the case where $H_0 = 0$![]() , this equation reduces to (29) of Jorge et al. (Reference Jorge, Sengupta and Landreman2020).
, this equation reduces to (29) of Jorge et al. (Reference Jorge, Sengupta and Landreman2020).
To conclude this section, we show that when $s_2 = 0$![]() , there is a simple relationship between the characteristics and Boozer angles. Choosing a value for $s_2$
, there is a simple relationship between the characteristics and Boozer angles. Choosing a value for $s_2$![]() is similar to gauge fixing, since a non-zero $s_2$
is similar to gauge fixing, since a non-zero $s_2$![]() simply represents a deviation of the ellipse from the upright position in the $(C_1,C_2)$
simply represents a deviation of the ellipse from the upright position in the $(C_1,C_2)$![]() plane. The orientation of the ellipse in real space is determined by $\sigma$
plane. The orientation of the ellipse in real space is determined by $\sigma$![]() , which is unaffected by changes in $s_2$
, which is unaffected by changes in $s_2$![]() , as long as the initial condition for $\varLambda$
, as long as the initial condition for $\varLambda$![]() is changed accordingly. The coordinates $x$
is changed accordingly. The coordinates $x$![]() and $y$
and $y$![]() can be written in terms of $C_1,C_2$
can be written in terms of $C_1,C_2$![]() as
as
Meanwhile, (1) and (54) from Jorge et al. (Reference Jorge, Sengupta and Landreman2020) give
Equating the two and using the relations between $\varLambda$![]() and $\sigma$
and $\sigma$![]() as well as $s_3$
as well as $s_3$![]() and $\bar {\eta }$
and $\bar {\eta }$![]() , we arrive at the following:
, we arrive at the following:
where $\vartheta = \theta _B - N\phi _B$![]() , with $\theta _B$
, with $\theta _B$![]() and $\phi _B$
and $\phi _B$![]() being the Boozer angles.
being the Boozer angles.
4 New classes of solutions
We now present three classes of exact and approximate solutions to (2.14) and (2.15) that fall outside the scope of the near-axis model. We will begin with a cubic polynomial solution with constant $H$![]() and then proceed to a non-polynomial solution and a solution with variable $H$
and then proceed to a non-polynomial solution and a solution with variable $H$![]() .
.
4.1 Cubic solution with finite pressure
Consider the following cubic polynomial in $C_1$![]() and $C_2$
and $C_2$![]() :
:

Inserting this ansatz into (2.14), the following is obtained:
where we have additionally assumed that $dp/d\varPsi = p_1 = \mathrm {const}$![]() , $H(\varPsi ) = H_0 = \mathrm {const}$
, $H(\varPsi ) = H_0 = \mathrm {const}$![]() and $a = a_2(l)x^2/2$
and $a = a_2(l)x^2/2$![]() . Only two terms in the above equation depend on $x$
. Only two terms in the above equation depend on $x$![]() ; equating those two terms, we get
; equating those two terms, we get
while the remaining terms match (3.2). Thus, a solution is obtained by first finding a quadratic solution, as discussed in § 3, and then adding a cubic term $r(\kappa x)^3$![]() with $r$
with $r$![]() given by (4.3). Equation (4.3) also imposes the constraint that $\kappa = \mathrm {const}$
given by (4.3). Equation (4.3) also imposes the constraint that $\kappa = \mathrm {const}$![]() , but, since $\tau$
, but, since $\tau$![]() is unconstrained, we can still get non-planar closed curves. At this point, we can see why $rC_1^3$
is unconstrained, we can still get non-planar closed curves. At this point, we can see why $rC_1^3$![]() is the only cubic term that we can include in (4.1). If we were to add cubic terms that involve $C_2$
is the only cubic term that we can include in (4.1). If we were to add cubic terms that involve $C_2$![]() , then (4.2) would also have terms that depend on $y$
, then (4.2) would also have terms that depend on $y$![]() and we would end up with an additional equation that would constrain $\tau$
and we would end up with an additional equation that would constrain $\tau$![]() , meaning that we would not be able to ensure that the axis is closed.
, meaning that we would not be able to ensure that the axis is closed.
Finally, note that while this cubic solution seems to be superficially similar to a second-order near-axis solution, there is a fundamental difference. Namely, the near-axis model assumes that the cubic term is a correction that is much smaller than the quadratic terms, whereas the present solution allows the cubic term to be of the same order as the quadratic ones. Also, unlike the second-order near-axis model, where the quasisymmetry error is $O(\epsilon ^3)$![]() , the present solution is still first order, so the quasisymmetry error will be $O(\epsilon ^2)$
, the present solution is still first order, so the quasisymmetry error will be $O(\epsilon ^2)$![]() .
.
4.2 Non-polynomial approximate solutions
In this subsection, we will show an approximate solution that consists of a rotating ellipse, which, as we have seen in the previous section, can be represented as a quadratic polynomial, and a non-polynomial perturbation. As we will perform a subsidiary expansion, it is convenient to rescale all quantities to be zeroth order in $\epsilon$![]() . Thus, after performing the following replacement: $\{\kappa,\bar {\eta },\tau,a_2,H_0,\varPsi,{\rm d}/{\rm d} l\}\mapsto \epsilon \{\kappa,\bar {\eta },\tau,a_2,H_0,\varPsi,{\rm d}/{\rm d} l\}$
. Thus, after performing the following replacement: $\{\kappa,\bar {\eta },\tau,a_2,H_0,\varPsi,{\rm d}/{\rm d} l\}\mapsto \epsilon \{\kappa,\bar {\eta },\tau,a_2,H_0,\varPsi,{\rm d}/{\rm d} l\}$![]() and $F_0\mapsto F_0/\epsilon$
and $F_0\mapsto F_0/\epsilon$![]() , we see that the $\epsilon$
, we see that the $\epsilon$![]() parameter is cancelled in (2.14) and the rotating ellipse solution (3.1).
parameter is cancelled in (2.14) and the rotating ellipse solution (3.1).
Now consider the case when $s_2 = 0$![]() ; then, using the expressions for the $s_i$
; then, using the expressions for the $s_i$![]() variables and $\varLambda$
variables and $\varLambda$![]() that we found in § 3, we have $s_3 = {\rm \pi}B_0\bar {\eta }^2/F_0$
that we found in § 3, we have $s_3 = {\rm \pi}B_0\bar {\eta }^2/F_0$![]() , $s_1 = {\rm \pi}B_0/(F_0\bar {\eta }^2)$
, $s_1 = {\rm \pi}B_0/(F_0\bar {\eta }^2)$![]() and $\varLambda = -\sigma /\bar {\eta }^2$
and $\varLambda = -\sigma /\bar {\eta }^2$![]() . The rotating ellipse solution can be represented as
. The rotating ellipse solution can be represented as
where the integration constants of the characteristics (2.16a,b) have been rescaled with respect to $\bar {\eta }$![]() :
:
yielding the normal form representation. We add to (4.4) a non-polynomial perturbation $f$![]() , and use the relation $F_0^{-1} = (\iota _0 - N)/(2{\rm \pi} B_0 r_0)$
, and use the relation $F_0^{-1} = (\iota _0 - N)/(2{\rm \pi} B_0 r_0)$![]() , which was found by Jorge et al. (Reference Jorge, Sengupta and Landreman2020), with $\iota _0$
, which was found by Jorge et al. (Reference Jorge, Sengupta and Landreman2020), with $\iota _0$![]() being the rotational transform on axis and $N$
being the rotational transform on axis and $N$![]() the helicity of the quasisymmetry. Here, the axis length $L$
the helicity of the quasisymmetry. Here, the axis length $L$![]() was replaced with the characteristic value of the minor radius $r_0 = \epsilon L/(2{\rm \pi} )$
was replaced with the characteristic value of the minor radius $r_0 = \epsilon L/(2{\rm \pi} )$![]() , due to $F_0$
, due to $F_0$![]() having been rescaled with respect to $\epsilon$
having been rescaled with respect to $\epsilon$![]() . The resulting ansatz is as follows:
. The resulting ansatz is as follows:

where $\kappa _0$![]() is the minimum value of $\kappa$
is the minimum value of $\kappa$![]() . Inserting this ansatz into the Grad–Shafranov equation (2.14), multiplying everything by $(\bar {\eta }/\kappa )^2$
. Inserting this ansatz into the Grad–Shafranov equation (2.14), multiplying everything by $(\bar {\eta }/\kappa )^2$![]() and using $a_2 = \kappa ^2 \,{\rm d}\varLambda /{\rm d} l - \tau = -(\kappa /\bar {\eta })^2 \,{\rm d}\sigma /{\rm d} l - \tau$
and using $a_2 = \kappa ^2 \,{\rm d}\varLambda /{\rm d} l - \tau = -(\kappa /\bar {\eta })^2 \,{\rm d}\sigma /{\rm d} l - \tau$![]() , the following is obtained:
, the following is obtained:

We can now carry out a subsidiary expansion in the limit of small $\bar {\eta }^2$![]() , i.e. $(\bar {\eta }/\kappa _0)^2 \ll 1$
, i.e. $(\bar {\eta }/\kappa _0)^2 \ll 1$![]() , but $(\bar {\eta }/\kappa _0)^4 > \epsilon$
, but $(\bar {\eta }/\kappa _0)^4 > \epsilon$![]() since we keep terms at that order in (4.6). This corresponds to the limit of a high aspect ratio stellarator with a highly elongated cross-section. Given that $\sigma \sim \bar {\eta }^2$
since we keep terms at that order in (4.6). This corresponds to the limit of a high aspect ratio stellarator with a highly elongated cross-section. Given that $\sigma \sim \bar {\eta }^2$![]() and $\iota _0 - N \sim \bar {\eta }^2$
and $\iota _0 - N \sim \bar {\eta }^2$![]() (Rodriguez Reference Rodriguez2022), the two lowest orders of the above equation are as follows:
(Rodriguez Reference Rodriguez2022), the two lowest orders of the above equation are as follows:

where $\sigma = \sigma _2 + \sigma _6$![]() with $\sigma _n\sim \bar {\eta }^n$
with $\sigma _n\sim \bar {\eta }^n$![]() , and $\iota _0 = N + \iota _{0,2} + \iota _{0,6}$
, and $\iota _0 = N + \iota _{0,2} + \iota _{0,6}$![]() with $\iota _{0,n}\sim \bar {\eta }^n$
with $\iota _{0,n}\sim \bar {\eta }^n$![]() . The values of $\iota _{0,n}$
. The values of $\iota _{0,n}$![]() are determined by enforcing periodicity on $\sigma _n$
are determined by enforcing periodicity on $\sigma _n$![]() : (4.8) is averaged over $l$
: (4.8) is averaged over $l$![]() , which removes $d\sigma _n/dl$
, which removes $d\sigma _n/dl$![]() ; the $\iota _{0,n}$
; the $\iota _{0,n}$![]() term must then be equal to the average of the right-hand side. Since we only solve (4.7) up to $O((\bar {\eta }/\kappa _0)^6)$
term must then be equal to the average of the right-hand side. Since we only solve (4.7) up to $O((\bar {\eta }/\kappa _0)^6)$![]() and $f$
and $f$![]() does not appear until $O((\bar {\eta }/\kappa _0)^8)$
does not appear until $O((\bar {\eta }/\kappa _0)^8)$![]() , we can treat $f$
, we can treat $f$![]() as a free function. If we were to attempt to solve this equation at $O((\bar {\eta }/\kappa _0)^8)$
as a free function. If we were to attempt to solve this equation at $O((\bar {\eta }/\kappa _0)^8)$![]() , then only the trivial solution $f'' = \mathrm {const}$
, then only the trivial solution $f'' = \mathrm {const}$![]() (i.e. $f$
(i.e. $f$![]() is a quadratic polynomial) would be permitted.
is a quadratic polynomial) would be permitted.
4.3 Approximate solution with variable $H$
We conclude this section by presenting a rotating ellipse approximate solution where $H(\varPsi ) = H_0 + H_1\varPsi$![]() . We also add a quartic term to $a$
. We also add a quartic term to $a$![]() : $a = a_2(l)x^2/2 + a_4(l)x^4/24$
: $a = a_2(l)x^2/2 + a_4(l)x^4/24$![]() , so the rescaled characteristics become
, so the rescaled characteristics become

Just like in the previous subsection, we rescale all quantities to be zeroth order in $\epsilon$![]() and let $s_2 = 0$
and let $s_2 = 0$![]() . In addition, we order $H_1\sim \bar {\eta }^2$
. In addition, we order $H_1\sim \bar {\eta }^2$![]() and $a_4\sim \bar {\eta }^2$
and $a_4\sim \bar {\eta }^2$![]() . It can now be seen that in the rotating ellipse ansatz (4.4), terms with $x$
. It can now be seen that in the rotating ellipse ansatz (4.4), terms with $x$![]() or $y$
or $y$![]() raised to a power higher than two only appear at order $(\bar {\eta }/\kappa _0)^6$
raised to a power higher than two only appear at order $(\bar {\eta }/\kappa _0)^6$![]() and higher. Thus, up to $O((\bar {\eta }/\kappa _0)^4)$
and higher. Thus, up to $O((\bar {\eta }/\kappa _0)^4)$![]() , it is still purely a rotating ellipse.
, it is still purely a rotating ellipse.
Inserting the rotating ellipse solution (4.4) with the new characteristics (4.9) into the Grad–Shafranov equation (2.14) and multiplying everything by $(\bar {\eta }/\kappa )^2$![]() , the following equation is obtained:
, the following equation is obtained:

where we have again used $a_2 = -(\kappa /\bar {\eta })^2 \,\textrm {d}\sigma /\textrm {d} l - \tau$![]() . Just as in the previous subsection, the above equation can be solved order by order. The three lowest orders are as follows:
. Just as in the previous subsection, the above equation can be solved order by order. The three lowest orders are as follows:

Thus, $\sigma$![]() is still determined by the same equations as (4.8); in addition to that, we also have an equation to determine $a_4$
is still determined by the same equations as (4.8); in addition to that, we also have an equation to determine $a_4$![]() .
.
5 Numerical example
While the model presented in this paper was derived with high-$\beta$![]() equilibria in mind, the only high-$\beta$
equilibria in mind, the only high-$\beta$![]() equilibrium that we have been able to find analytically is the constant curvature one presented in § 4.1. In this section, we will instead illustrate the approximate solution discussed in § 4.2 with a numerical example of a quasiaxisymmetric ($N=0$
equilibrium that we have been able to find analytically is the constant curvature one presented in § 4.1. In this section, we will instead illustrate the approximate solution discussed in § 4.2 with a numerical example of a quasiaxisymmetric ($N=0$![]() ) device. This approximate solution has another important property that we wanted our model to include: non-zero shear. We were unable to get a numerical equilibrium with high $\beta$
) device. This approximate solution has another important property that we wanted our model to include: non-zero shear. We were unable to get a numerical equilibrium with high $\beta$![]() because VMEC failed to find a solution for all of the non-planar constant curvature axes that we could find, due to their high shaping. We leave the numerical verification of the analytical solution in § 4.1, as well as the numerical search for other high-$\beta$
because VMEC failed to find a solution for all of the non-planar constant curvature axes that we could find, due to their high shaping. We leave the numerical verification of the analytical solution in § 4.1, as well as the numerical search for other high-$\beta$![]() solutions for future work.
solutions for future work.
The example is constructed by numerically solving (4.8), and is then compared with both VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983) results and the closest near-axis approximation, which is identical to taking $f=0$![]() . The pyQSC code (Reference Landreman, Jorge, Rodriguez and DudtLandreman et al. 2020–2023) was used to solve the $\sigma$
. The pyQSC code (Reference Landreman, Jorge, Rodriguez and DudtLandreman et al. 2020–2023) was used to solve the $\sigma$![]() equations and generate VMEC input files, based on the method described by Landreman & Sengupta (Reference Landreman and Sengupta2019).
equations and generate VMEC input files, based on the method described by Landreman & Sengupta (Reference Landreman and Sengupta2019).
While the solution in § 4.2 allows for arbitrary $f$![]() , here we will consider a sixth-order polynomial, $f(c) = (0.3\,\mathrm {m}^{-2})c^4 + (0.3\,\mathrm {m}^{-4})c^6$
, here we will consider a sixth-order polynomial, $f(c) = (0.3\,\mathrm {m}^{-2})c^4 + (0.3\,\mathrm {m}^{-4})c^6$![]() , where $c = c_2 + \sigma _0 c_1$
, where $c = c_2 + \sigma _0 c_1$![]() ; this is higher order than the cubic polynomials of the second-order near-axis model. We consider a four-field-period solution with $\bar {\eta } = 2.01735426\times 10^{-2}\,\mathrm {m}^{-1}$
; this is higher order than the cubic polynomials of the second-order near-axis model. We consider a four-field-period solution with $\bar {\eta } = 2.01735426\times 10^{-2}\,\mathrm {m}^{-1}$![]() , $B_0 = 1$
, $B_0 = 1$![]() T, $H_0 = 0$
T, $H_0 = 0$![]() . Equations (4.8) result in rotational transforms $\iota _{0,2} = 0.188923174$
. Equations (4.8) result in rotational transforms $\iota _{0,2} = 0.188923174$![]() and $\iota _{0,6} = -0.031115615$
and $\iota _{0,6} = -0.031115615$![]() . The axis shape given by
. The axis shape given by

where $R$![]() and $z$
and $z$![]() are the cylindrical coordinates in metres. The value of $(\bar {\eta }/\kappa _0)^2$
are the cylindrical coordinates in metres. The value of $(\bar {\eta }/\kappa _0)^2$![]() for this axis is approximately 0.3. The VMEC equilibrium, obtained by constructing the $F_0\varPsi /{\rm \pi} = 4\,\mathrm {T}\,\textrm {m}^2$
for this axis is approximately 0.3. The VMEC equilibrium, obtained by constructing the $F_0\varPsi /{\rm \pi} = 4\,\mathrm {T}\,\textrm {m}^2$![]() surface using (4.6) and passing it to VMEC as the boundary, is shown in figure 1. The aspect ratio of the resulting stellarator is 16.5. The assumption $\textrm {d} p/\textrm {d}\varPsi = 0$
surface using (4.6) and passing it to VMEC as the boundary, is shown in figure 1. The aspect ratio of the resulting stellarator is 16.5. The assumption $\textrm {d} p/\textrm {d}\varPsi = 0$![]() , made when constructing the base solution in § 3, and the choice of $H_0$
, made when constructing the base solution in § 3, and the choice of $H_0$![]() correspond to pressure and toroidal current profiles of zero; this was specified in the VMEC input. The total toroidal flux in the VMEC input was determined by multiplying $B_0$
correspond to pressure and toroidal current profiles of zero; this was specified in the VMEC input. The total toroidal flux in the VMEC input was determined by multiplying $B_0$![]() by the plasma cross-section area in the plane perpendicular to the axis.
by the plasma cross-section area in the plane perpendicular to the axis.

Figure 1. The outermost flux surface of the VMEC equilibrium based on the solution with a sixth-order polynomial perturbation. Colour represents $|\boldsymbol {B}|$![]() .
.
Figure 2(a,b) compares the flux surfaces of the present Grad–Shafranov model, obtained from (4.6), to both the flux surfaces calculated by VMEC and the flux surfaces of the closest near-axis approximation, as given by (4.4). All flux surfaces are shown on the $\phi = 0$![]() poloidal plane. As expected, near the axis, the near-axis flux surfaces closely match those of the Grad–Shafranov model, but further away from the axis, the Grad–Shafranov surfaces become non-elliptic as the contribution from $f$
poloidal plane. As expected, near the axis, the near-axis flux surfaces closely match those of the Grad–Shafranov model, but further away from the axis, the Grad–Shafranov surfaces become non-elliptic as the contribution from $f$![]() becomes non-negligible. Figure 2(c) compares the $\iota$
becomes non-negligible. Figure 2(c) compares the $\iota$![]() profiles in the near-axis and Grad–Shafranov models. These are computed numerically by first calculating the toroidal flux $\psi$
profiles in the near-axis and Grad–Shafranov models. These are computed numerically by first calculating the toroidal flux $\psi$![]() at each value of $\varPsi$
at each value of $\varPsi$![]() , then finding $F = \textrm {d}\varPsi /\textrm {d}\psi$
, then finding $F = \textrm {d}\varPsi /\textrm {d}\psi$![]() and using the formula
and using the formula
which is given by Helander (Reference Helander2014) as an unnumbered equation. Again, these agree well with each other and the $\iota _0$![]() constant near the axis, but the Grad–Shafranov solution has a noticeable shear. The $\iota$
constant near the axis, but the Grad–Shafranov solution has a noticeable shear. The $\iota$![]() profiles calculated by VMEC (not shown here) do not match the Grad–Shafranov and near-axis profiles shown in figure 2(c), with the $\iota$
profiles calculated by VMEC (not shown here) do not match the Grad–Shafranov and near-axis profiles shown in figure 2(c), with the $\iota$![]() on axis in the corresponding VMEC solutions being greater by approximately 0.06 and 0.024, respectively. A similar mismatch with VMEC has been observed by Sengupta et al. (Reference Sengupta, Rodriguez, Jorge, Landreman and Bhattacharjee2024b); it likely appears because the boundary (and not the axis) is fixed in VMEC, so for a finite aspect ratio, the VMEC axis does not match the axis given by (5.1). There are also additional complications arising from VMEC having a coordinate singularity on the axis (Panici et al. Reference Panici, Conlin, Dudt, Unalmis and Kolemen2023a). Just as was reported by Sengupta et al. (Reference Sengupta, Rodriguez, Jorge, Landreman and Bhattacharjee2024b), the agreement between the $\iota$
on axis in the corresponding VMEC solutions being greater by approximately 0.06 and 0.024, respectively. A similar mismatch with VMEC has been observed by Sengupta et al. (Reference Sengupta, Rodriguez, Jorge, Landreman and Bhattacharjee2024b); it likely appears because the boundary (and not the axis) is fixed in VMEC, so for a finite aspect ratio, the VMEC axis does not match the axis given by (5.1). There are also additional complications arising from VMEC having a coordinate singularity on the axis (Panici et al. Reference Panici, Conlin, Dudt, Unalmis and Kolemen2023a). Just as was reported by Sengupta et al. (Reference Sengupta, Rodriguez, Jorge, Landreman and Bhattacharjee2024b), the agreement between the $\iota$![]() on axis in VMEC and that predicted by the Grad–Shafranov model improves as the aspect ratio is increased. Finally, figure 3 shows that the maximum quasisymmetry error, defined as
on axis in VMEC and that predicted by the Grad–Shafranov model improves as the aspect ratio is increased. Finally, figure 3 shows that the maximum quasisymmetry error, defined as

and calculated in VMEC equilibria with varying aspect ratios, scales as $\epsilon ^2$![]() . Here, $\hat {B}_{n,m}(\psi )$
. Here, $\hat {B}_{n,m}(\psi )$![]() are the Fourier modes of $|\boldsymbol {B}|$
are the Fourier modes of $|\boldsymbol {B}|$![]() on flux surface $\psi$
on flux surface $\psi$![]() . This behaviour is to be expected, since we have only ensured quasisymmetry at order $\epsilon$
. This behaviour is to be expected, since we have only ensured quasisymmetry at order $\epsilon$![]() .
.

Figure 2. (a) A comparison of the flux surfaces computed from (4.6) (lines) to the closest near-axis approximation (dots). (b) Flux surfaces computed from (4.6) (lines) compared with the flux surfaces computed by VMEC (dots). The flux surfaces are shown for $F_0\varPsi /{\rm \pi} = 0.1, 0.3, 0.5, 1, 2, 4\,\mathrm {T}\,\textrm {m}^2$![]() . (c) $\iota$
. (c) $\iota$![]() profiles computed in the Grad–Shafranov model, the near-axis model and the constant $\iota _0$
profiles computed in the Grad–Shafranov model, the near-axis model and the constant $\iota _0$![]() .
.

Figure 3. Maximum quasisymmetry error (black dots) scales as $\epsilon ^2$![]() (dashed blue line is $10\epsilon ^2$
(dashed blue line is $10\epsilon ^2$![]() ).
).
6 Conclusion
We have derived a first-order asymptotic model for high-$\beta$![]() ($\beta = O(\epsilon )$
($\beta = O(\epsilon )$![]() ) quasisymmetric stellarators under the assumption that the vacuum magnetic field is dominant (${\epsilon \ll 1}$
) quasisymmetric stellarators under the assumption that the vacuum magnetic field is dominant (${\epsilon \ll 1}$![]() ), but non-vacuum effects can still contribute ($\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(\epsilon )$
), but non-vacuum effects can still contribute ($\boldsymbol {\nabla }\chi \boldsymbol {\cdot }\boldsymbol {\nabla } = O(\epsilon )$![]() ). We have shown that these assumptions require the aspect ratio to be large and a simple expression is obtained for the lowest-order vacuum field ($\boldsymbol {\nabla }\chi = B_0\boldsymbol {\nabla } l$
). We have shown that these assumptions require the aspect ratio to be large and a simple expression is obtained for the lowest-order vacuum field ($\boldsymbol {\nabla }\chi = B_0\boldsymbol {\nabla } l$![]() ). The first-order correction, which involves both vacuum and current-driven fields, is then governed by a Grad–Shafranov equation and the requirement that flux surfaces exist ($\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$
). The first-order correction, which involves both vacuum and current-driven fields, is then governed by a Grad–Shafranov equation and the requirement that flux surfaces exist ($\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$![]() ). Unlike the more simple near-axisymmetric case considered in our previous work (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), which is a special case of the present model, the overconstraining problem cannot be resolved in general. Thus, one must look for special solutions that satisfy both equations simultaneously. One family of such solutions, and thus another special case of this model, is the first-order quasisymmetric near-axis solutions.
). Unlike the more simple near-axisymmetric case considered in our previous work (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), which is a special case of the present model, the overconstraining problem cannot be resolved in general. Thus, one must look for special solutions that satisfy both equations simultaneously. One family of such solutions, and thus another special case of this model, is the first-order quasisymmetric near-axis solutions.
We also provide several new solutions which are outside the scope of both the near-axis model and our previous near-axisymmetric model, and show a numerical example of one of these new solutions. When comparing the numerical results from the present model to VMEC, the flux surfaces match well, but the $\iota$![]() profiles show a mismatch which decreases as the aspect ratio is increased. The mismatch is most likely due to VMEC shifting the axis during minimization, so the VMEC axis does not exactly match the axis used when solving the Grad–Shafranov equation. We plan to use DESC in future work to re-evaluate the agreement between $\iota$
profiles show a mismatch which decreases as the aspect ratio is increased. The mismatch is most likely due to VMEC shifting the axis during minimization, so the VMEC axis does not exactly match the axis used when solving the Grad–Shafranov equation. We plan to use DESC in future work to re-evaluate the agreement between $\iota$![]() profiles. DESC has the option of fixing the axis (Panici et al. Reference Panici, Rodriguez, Conlin, Kim, Dudt, Unalmis and Kolemen2023b) and avoids large errors on axis, which are typical for VMEC, by using Zernike polynomials (Panici et al. Reference Panici, Conlin, Dudt, Unalmis and Kolemen2023a). Finally, DESC can handle highly shaped axes better than VMEC, and is a more appropriate tool for doing a numerical verification of the analytical solution in § 4.1, as all of the non-planar constant curvature axes that we have found so far are highly shaped.
profiles. DESC has the option of fixing the axis (Panici et al. Reference Panici, Rodriguez, Conlin, Kim, Dudt, Unalmis and Kolemen2023b) and avoids large errors on axis, which are typical for VMEC, by using Zernike polynomials (Panici et al. Reference Panici, Conlin, Dudt, Unalmis and Kolemen2023a). Finally, DESC can handle highly shaped axes better than VMEC, and is a more appropriate tool for doing a numerical verification of the analytical solution in § 4.1, as all of the non-planar constant curvature axes that we have found so far are highly shaped.
We expect that the analytical solutions found in this paper are only a small subset of all possible solutions to the model we derived. In future work, we plan to implement a numerical solver that will look for solutions by constructing a function basis in $C_1,C_2$![]() space and looking for functions and boundary shapes that minimize the residual in the Grad–Shafranov equation (2.14).
space and looking for functions and boundary shapes that minimize the residual in the Grad–Shafranov equation (2.14).
Another line of work that we intend to pursue is the construction of a similar model in the low-$\beta$![]() ($\beta = O(\epsilon ^2)$
($\beta = O(\epsilon ^2)$![]() ) regime. As discussed in § 2, in the low-$\beta$
) regime. As discussed in § 2, in the low-$\beta$![]() regime, there are no constraints on $\chi$
regime, there are no constraints on $\chi$![]() , aside from satisfying the Laplace equation. This allows for a richer set of solutions, including compact stellarators, at the expense of analytical progress being more difficult. Nevertheless, as will be shown in a future publication, some analytical progress, such as finding the characteristics of the $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$
, aside from satisfying the Laplace equation. This allows for a richer set of solutions, including compact stellarators, at the expense of analytical progress being more difficult. Nevertheless, as will be shown in a future publication, some analytical progress, such as finding the characteristics of the $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$![]() equation, is still possible. Finally, the low-$\beta$
equation, is still possible. Finally, the low-$\beta$![]() model is closely related to the reduced MHD model implemented in the JOREK code (Hoelzl et al. Reference Hoelzl, Huijsmans, Pamela, Bécoulet, Nardon, Artola, Nkonga, Atanasiu, Bandaru and Bhole2021; Nikulsin Reference Nikulsin2021; Nikulsin et al. Reference Nikulsin, Hoelzl, Zocco, Lackner and Günter2021), with the main difference being that the JOREK models use an ansatz instead of an ordering. Implementing a numerical solver for this model will allow one to initialize JOREK simulations of quasisymmetric stellarators from the Grad–Shafranov solutions instead of importing GVEC equilibria.
model is closely related to the reduced MHD model implemented in the JOREK code (Hoelzl et al. Reference Hoelzl, Huijsmans, Pamela, Bécoulet, Nardon, Artola, Nkonga, Atanasiu, Bandaru and Bhole2021; Nikulsin Reference Nikulsin2021; Nikulsin et al. Reference Nikulsin, Hoelzl, Zocco, Lackner and Günter2021), with the main difference being that the JOREK models use an ansatz instead of an ordering. Implementing a numerical solver for this model will allow one to initialize JOREK simulations of quasisymmetric stellarators from the Grad–Shafranov solutions instead of importing GVEC equilibria.
Acknowledgements
The authors thank P. Helander, S. Buller, E. Paul, E. Rodriguez, A. Brown, S. Hudson, M. Landreman, F.P. Diaz, H. Zhu and V. Duarte for fruitful discussions.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Funding
This research was supported by a grant from the Simons Foundation/SFARI (560651, AB) and the Department of Energy Award No. DE-SC0024548.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Perpendicular force balance terms with general $B_v$
In this appendix, we will provide a rigorous proof that the two terms in (2.4) are linearly independent when $B_v \neq B_0 + O(\epsilon )$![]() . First, suppose that the two terms are not linearly independent; then we can write
. First, suppose that the two terms are not linearly independent; then we can write
where $f$![]() and $g$
and $g$![]() are some functions to be determined. If the above equation holds, then the left-hand side should be orthogonal to its own curl:
are some functions to be determined. If the above equation holds, then the left-hand side should be orthogonal to its own curl:
Thus, $B_1$![]() must be a function of only $p$
must be a function of only $p$![]() and $B_v$
and $B_v$![]() . Using this fact and dotting (A1) with $\boldsymbol {\nabla } p\times \boldsymbol {\nabla } B_v$
. Using this fact and dotting (A1) with $\boldsymbol {\nabla } p\times \boldsymbol {\nabla } B_v$![]() , we get $\boldsymbol {\nabla } g\boldsymbol {\cdot }(\boldsymbol {\nabla } p\times \boldsymbol {\nabla } B_v) = 0$
, we get $\boldsymbol {\nabla } g\boldsymbol {\cdot }(\boldsymbol {\nabla } p\times \boldsymbol {\nabla } B_v) = 0$![]() if $f \neq 0$
if $f \neq 0$![]() ; thus $g$
; thus $g$![]() must also be a function of only $p$
must also be a function of only $p$![]() and $B_v$
and $B_v$![]() .
.
For (2.4) to be satisfied, we must have either $f=0$![]() or $g=\mathrm {const}$
or $g=\mathrm {const}$![]() or $g = g(\chi )$
or $g = g(\chi )$![]() . Consider the latter case first. Since $g(\chi ) = g(p,B_v)$
. Consider the latter case first. Since $g(\chi ) = g(p,B_v)$![]() , this is an equation that can be solved for $B_v$
, this is an equation that can be solved for $B_v$![]() , giving $B_v = B_v(p,\chi )$
, giving $B_v = B_v(p,\chi )$![]() . If we insert this into the quasisymmetry condition (2.7a), we will get $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\chi ~\partial B_v/\partial \chi = 0$
. If we insert this into the quasisymmetry condition (2.7a), we will get $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\chi ~\partial B_v/\partial \chi = 0$![]() since $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } p = 0$
since $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } p = 0$![]() , meaning that $B_v$
, meaning that $B_v$![]() must be a flux function, which is a contradiction since $|\boldsymbol {B}| = B_v + O(\epsilon ^2)$
must be a flux function, which is a contradiction since $|\boldsymbol {B}| = B_v + O(\epsilon ^2)$![]() and $|\boldsymbol {B}|$
and $|\boldsymbol {B}|$![]() can only be a flux function in axisymmetry (Schief Reference Schief2003).
can only be a flux function in axisymmetry (Schief Reference Schief2003).
Alternatively, if either $f=0$![]() or $g=\mathrm {const}$
or $g=\mathrm {const}$![]() , (A1) will have the following two components in the $\boldsymbol {\nabla } p$
, (A1) will have the following two components in the $\boldsymbol {\nabla } p$![]() and $\boldsymbol {\nabla } B_v$
and $\boldsymbol {\nabla } B_v$![]() directions:
directions:
These two equations for $B_1$![]() are incompatible. Integrating the first one, we get $B_1/\mu _0 = -p/B_v + u(B_v)$
are incompatible. Integrating the first one, we get $B_1/\mu _0 = -p/B_v + u(B_v)$![]() , where $u$
, where $u$![]() is an arbitrary function. Inserting this into the second equation, we get $u' - u/B_v = -2p/B_v^2$
is an arbitrary function. Inserting this into the second equation, we get $u' - u/B_v = -2p/B_v^2$![]() , which is a contradiction since $u$
, which is a contradiction since $u$![]() cannot depend on $p$
cannot depend on $p$![]() . Finally, note that the contradiction is resolved if $B_v = B_0 + O(\epsilon )$
. Finally, note that the contradiction is resolved if $B_v = B_0 + O(\epsilon )$![]() , since $\boldsymbol {\nabla } B_v = O(\epsilon )$
, since $\boldsymbol {\nabla } B_v = O(\epsilon )$![]() in that case, which will remove the second equation, while the solution to the first equation will become the pressure-balance relation (2.5).
in that case, which will remove the second equation, while the solution to the first equation will become the pressure-balance relation (2.5).
Appendix B. Near-axisymmetric and near-helically-symmetric solutions
Previously (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), we derived a condition for consistency between the Grad–Shafranov equation and the $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$![]() equation, and then used it to obtain a condition on $a$
equation, and then used it to obtain a condition on $a$![]() under which the two equations are consistent for all solutions $\varPsi$
under which the two equations are consistent for all solutions $\varPsi$![]() . We can attempt a similar approach for the present model, but it will exclude many solutions of interest, including all solutions discussed in §§ 3 and 4.
. We can attempt a similar approach for the present model, but it will exclude many solutions of interest, including all solutions discussed in §§ 3 and 4.
To obtain the consistency condition, we apply the $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() operator to (2.14), and commute $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$
operator to (2.14), and commute $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }$![]() with $\varDelta _\perp$
with $\varDelta _\perp$![]() :
:
The whole equation must be satisfied if (2.14) is satisfied; however, the first term must be individually zero since $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }\varPsi = 0$![]() . Removing the first term and working out the commutator, the following consistency condition is obtained:
. Removing the first term and working out the commutator, the following consistency condition is obtained:

The only case where it is satisfied independent of $\varPsi$![]() is if $a(x,l) = a_0(l) + xa_1(l) - \tau x^2/2$
is if $a(x,l) = a_0(l) + xa_1(l) - \tau x^2/2$![]() and $\textrm {d}\tau /\textrm {d} l = \textrm {d}\kappa /\textrm {d} l = O(\epsilon ^3)$
and $\textrm {d}\tau /\textrm {d} l = \textrm {d}\kappa /\textrm {d} l = O(\epsilon ^3)$![]() . When $\tau = 0$
. When $\tau = 0$![]() and $\kappa = 1/R_0$
and $\kappa = 1/R_0$![]() , this consistency condition reduces to that derived previously (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), which limited the stellarator to being a perturbed tokamak. In addition to the vertical perturbation discussed previously (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), the condition above explicitly allows the tokamak to be perturbed in the $R$
, this consistency condition reduces to that derived previously (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), which limited the stellarator to being a perturbed tokamak. In addition to the vertical perturbation discussed previously (Sengupta et al. Reference Sengupta, Nikulsin, Gaur and Bhattacharjee2024a), the condition above explicitly allows the tokamak to be perturbed in the $R$![]() -direction; such a perturbation, if it is of the order of the minor radius, will result in an $O(\epsilon ^2)$
-direction; such a perturbation, if it is of the order of the minor radius, will result in an $O(\epsilon ^2)$![]() correction to $\kappa$
correction to $\kappa$![]() , which still satisfies $\textrm {d}\kappa /\textrm {d} l = O(\epsilon ^3)$
, which still satisfies $\textrm {d}\kappa /\textrm {d} l = O(\epsilon ^3)$![]() . Finally, when $\tau \neq 0$
. Finally, when $\tau \neq 0$![]() , the axis becomes an open helix, which corresponds to the straight stellarator limit. Similar to the tokamak, the straight stellarator can be perturbed in both the normal and binormal directions by manipulating $\kappa$
, the axis becomes an open helix, which corresponds to the straight stellarator limit. Similar to the tokamak, the straight stellarator can be perturbed in both the normal and binormal directions by manipulating $\kappa$![]() and $a_1$
and $a_1$![]() .
.