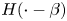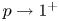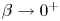1. Introduction
In this work we study the following quasilinear elliptic equation

where the 1-Laplacian operator is formally defined as $\Delta _1 u = \mbox {div}(Du/|Du|)$![]() , $\Omega \subset \mathbb {R}^N$
, $\Omega \subset \mathbb {R}^N$![]() is a bounded domain with a Lipschitz boundary, $N \geq 2$
is a bounded domain with a Lipschitz boundary, $N \geq 2$![]() , $1 < q < N/(N-1),$
, $1 < q < N/(N-1),$![]() $\beta >0$
$\beta >0$![]() is a real parameter and $H: \mathbb {R}\rightarrow \mathbb {R}$
is a real parameter and $H: \mathbb {R}\rightarrow \mathbb {R}$![]() is the Heaviside function $H(t) = 1$
is the Heaviside function $H(t) = 1$![]() if $t \geq 0$
if $t \geq 0$![]() and $H(t) = 0$
and $H(t) = 0$![]() otherwise.
otherwise.
In recent decades, the study of nonlinear partial differential equations with discontinuous nonlinearities has attracted the attention of several researchers. One of the reasons to study such equations is due to many free boundary problems arising in mathematical physics which can be stated in this form. Among these problems, we have the obstacle problem, the seepage surface problem, and the Elenbaas equation, see [Reference Chang15–Reference Chang17]. For more applications see [Reference Ambrosetti, Calahorrano and Dobarro4]. Several techniques have been developed or applied to study this kind of problem, such as variational methods for nondifferentiable functionals, lower and upper solutions, dual variational principle, global branching, Palais principle of symmetric criticality for locally Lipschitz functional and the theory of multivalued mappings. See for instance, Alves, Yuan and Huang [Reference Alves, Yuan and Huang1], Alves, Santos and Nemer [Reference Alves, dos Santos and Nemer2], Ambrosetti and Badiale [Reference Ambrosetti and Badiale3], Ambrosetti, Calahorrano and Dobarro [Reference Ambrosetti, Calahorrano and Dobarro4], Ambrosetti and Turner [Reference Ambrosetti and Turner5], Anmin and Chang [Reference Anmin and Chang11], Arcoya and Calahorrano [Reference Arcoya and Calahorrano13], Cerami [Reference Cerami14], Chang [Reference Chang15–Reference Chang17], Clarke [Reference Clarke20, Reference Clarke21], Gazzola and Rădulescu [Reference Gazzola and Rădulescu24], Krawcewicz and Marzantowicz [Reference Krawcewicz and Marzantowicz28], Molica Bisci and Repovš [Reference Bisci and Repovš30], Rădulescu [Reference Rădulescu34], dos Santos and Figueiredo [Reference Figueiredo and dos Santos23] and their references.
As far as problems involving the 1-Laplacian operator are concerned, there are at least two approaches one can follow. The first one is based on the study of the energy functional associated to the problem, which is defined in $BV(\Omega )$![]() , whenever one can write it as the difference of a convex and locally Lipschitz functional and a $C^1$
, whenever one can write it as the difference of a convex and locally Lipschitz functional and a $C^1$![]() one. Then, one can use the tools of nonsmooth nonlinear analysis (see [Reference Chang17, Reference Clarke21, Reference Szulkin33]) to find critical points of such energy functional. Note that, in studying (1.1), this is far from being an option for us, since the energy functional associated to (1.1) would be defined in $BV(\Omega )$
one. Then, one can use the tools of nonsmooth nonlinear analysis (see [Reference Chang17, Reference Clarke21, Reference Szulkin33]) to find critical points of such energy functional. Note that, in studying (1.1), this is far from being an option for us, since the energy functional associated to (1.1) would be defined in $BV(\Omega )$![]() , and given by
, and given by
where $\mathcal {F}_\beta (u)\,{=}\,\int _{\Omega } F_H(u)\,{\rm d}x$![]() , with $f_H(s)\,{=}\,H(s\,{-}\,\beta )|s|^{q-2}s$
, with $f_H(s)\,{=}\,H(s\,{-}\,\beta )|s|^{q-2}s$![]() and $F_H(t) \,{=}\, \int _0^t f_H(s)\,{\rm d}x$
and $F_H(t) \,{=}\, \int _0^t f_H(s)\,{\rm d}x$![]() . Hence, since $\mathcal {F}_\beta$
. Hence, since $\mathcal {F}_\beta$![]() is not a $C^1$
is not a $C^1$![]() functional defined on $BV(\Omega )$
functional defined on $BV(\Omega )$![]() , it would be tricky to show that a critical point of $I_H$
, it would be tricky to show that a critical point of $I_H$![]() satisfies (1.1) in some sense, since in this case, we could not use variational inequalities to follow the standard approach, which is based on that one proposed by [Reference Szulkin33].
satisfies (1.1) in some sense, since in this case, we could not use variational inequalities to follow the standard approach, which is based on that one proposed by [Reference Szulkin33].
Fortunately, there is another approach which is based on the study of (1.1), with the 1-Laplacian substituted by the p-Laplacian operator, for $p > 1$![]() . Then, one can use standard arguments to solve the associated problem and then studying the family of such solutions as $p \to 1^+$
. Then, one can use standard arguments to solve the associated problem and then studying the family of such solutions as $p \to 1^+$![]() . To the best of our knowledge, the pioneering works involving this operator were written by F. Andreu, C. Ballesteler, V. Caselles and J.M. Mazón in a series of papers (among them [Reference Andreu, Ballester, Caselles and Mazón7–Reference Andreu, Ballester, Caselles and Mazón9]), which gave rise to the monograph [Reference Andreu, Caselles and Mazón10]. Among the very first works on this issue we should also cite the works of Kawohl [Reference Kawohl27] and Demengel [Reference Demengel22].
. To the best of our knowledge, the pioneering works involving this operator were written by F. Andreu, C. Ballesteler, V. Caselles and J.M. Mazón in a series of papers (among them [Reference Andreu, Ballester, Caselles and Mazón7–Reference Andreu, Ballester, Caselles and Mazón9]), which gave rise to the monograph [Reference Andreu, Caselles and Mazón10]. Among the very first works on this issue we should also cite the works of Kawohl [Reference Kawohl27] and Demengel [Reference Demengel22].
Before to state our main result, let us define what we mean by a solution of the problem (1.1). Inspired by locally Lipschitz continuous functionals [Reference Chang17, Reference Clarke20, Reference Clarke21, Reference Grossinho and Tersian26] and Anzellotti–Frid–Chen's Pairing Theory [Reference Anzellotti12, Reference Chen and Frid19] (see subsections 2.2 and 2.1 for more details), we say that $u \in BV(\Omega )$![]() is a bounded variation solution of (1.1), if there exist $\rho \in L^{\frac {q}{q-1}}(\Omega )$
is a bounded variation solution of (1.1), if there exist $\rho \in L^{\frac {q}{q-1}}(\Omega )$![]() and ${\textbf z} \in X_N(\Omega )$
and ${\textbf z} \in X_N(\Omega )$![]() with $\|{\textbf z}\|_\infty \leq 1$
with $\|{\textbf z}\|_\infty \leq 1$![]() , such that
, such that

and it holds that, for almost every $x\in \Omega,$![]()

It is important to point out here that if the set $\{x\in \Omega : u(x)=\beta \}$![]() has zero Lebesgue measure, then $\rho (x)=H(u(x)-\beta )|u(x)|^{q-2}u(x)$
has zero Lebesgue measure, then $\rho (x)=H(u(x)-\beta )|u(x)|^{q-2}u(x)$![]() for almost every $x\in \Omega$
for almost every $x\in \Omega$![]() .
.
Motivated by the works previously mentioned, our first main result is the following.
Theorem 1.1 Suppose that $N \geq 2$![]() and $1 < q < N/(N-1)$
and $1 < q < N/(N-1)$![]() . Then, for each $\beta > 0,$
. Then, for each $\beta > 0,$![]() (1.1) admits at least one nonnegative and nontrivial solution $u_\beta \in BV(\Omega )\cap L^{\infty }(\Omega ),$
(1.1) admits at least one nonnegative and nontrivial solution $u_\beta \in BV(\Omega )\cap L^{\infty }(\Omega ),$![]() in the sense of (1.2).
in the sense of (1.2).
In the scope of the last theorem, a question which naturally arises is about the behaviour of the solutions $u_\beta$![]() , as $\beta \to 0^+$
, as $\beta \to 0^+$![]() . In fact, one should expect that $u_\beta$
. In fact, one should expect that $u_\beta$![]() converges in some sense, as $\beta \to 0^+$
converges in some sense, as $\beta \to 0^+$![]() , to a solution of the following problem
, to a solution of the following problem

In the next theorem, we prove that this in fact occurs.
Theorem 1.2 For each $\beta > 0,$![]() let $u_\beta$
let $u_\beta$![]() be the solution given in theorem 1.1. Then there exists a nontrivial and nonnegative solution of (1.4) , $u_0 \in BV(\Omega ),$
be the solution given in theorem 1.1. Then there exists a nontrivial and nonnegative solution of (1.4) , $u_0 \in BV(\Omega ),$![]() such that, as $\beta \to 0^+,$
such that, as $\beta \to 0^+,$![]()
Moreover, there exist positive constants $\mu$![]() and $\beta _{0},$
and $\beta _{0},$![]() such that
such that
where $|A|$![]() denotes the measure of a measurable set $A\subset \mathbb {R}^N$
denotes the measure of a measurable set $A\subset \mathbb {R}^N$![]() .
.
Note that the last part of the theorem guarantees that the set $\{u_\beta > \beta \}$![]() does not shrink as $\beta \to 0$
does not shrink as $\beta \to 0$![]() , that is, $\|u_\beta \|_{L^\infty (\Omega )}> \beta$
, that is, $\|u_\beta \|_{L^\infty (\Omega )}> \beta$![]() , for $\beta$
, for $\beta$![]() small enough. Such an information is quite relevante because it ensures that, at least for $\beta$
small enough. Such an information is quite relevante because it ensures that, at least for $\beta$![]() small, $u_{\beta }$
small, $u_{\beta }$![]() is in fact a solution of a problem involving a discontinuous nonlinearity.
is in fact a solution of a problem involving a discontinuous nonlinearity.
The existence of positive solution for (1.1) with $\beta =0$![]() (i.e., (1.4)) was recently studied by Molino-Segura in [Reference Segura de León and Molino Salas32]. Due to the discontinuity in (1.1), caused by the Heaviside function (with $\beta >0$
(i.e., (1.4)) was recently studied by Molino-Segura in [Reference Segura de León and Molino Salas32]. Due to the discontinuity in (1.1), caused by the Heaviside function (with $\beta >0$![]() ), we cannot use the classical critical point theory for $C^1$
), we cannot use the classical critical point theory for $C^1$![]() functionals as in [Reference Segura de León and Molino Salas32]. For this reason, motivated by [Reference Ambrosetti and Turner5, Reference Arcoya and Calahorrano13, Reference Chang17, Reference Chang18, Reference Clarke20, Reference Clarke21], we combine variational methods for nondifferentiable functionals with the approximation argument of [Reference Segura de León and Molino Salas32].
functionals as in [Reference Segura de León and Molino Salas32]. For this reason, motivated by [Reference Ambrosetti and Turner5, Reference Arcoya and Calahorrano13, Reference Chang17, Reference Chang18, Reference Clarke20, Reference Clarke21], we combine variational methods for nondifferentiable functionals with the approximation argument of [Reference Segura de León and Molino Salas32].
In theorem 1.1, to prove the boundedness of the solutions, we use Moser's iteration method (see [Reference Moser31]) and a careful analysis of some constants to obtain a uniform estimate in the $L^\infty (\Omega )-$![]() norm of the solutions of the approximate problem. These estimates were essential in our arguments to ensure that the solution of problem (1.1) is nontrivial.
norm of the solutions of the approximate problem. These estimates were essential in our arguments to ensure that the solution of problem (1.1) is nontrivial.
This paper is organized as follows. In § 2 we present some definitions and basic results about functions of bounded variation and the nonlinear analysis involving nonsmooth functionals. In § 3 and 4, we present the proofs of theorem 1.1 and 1.2, respectively.
2. Preliminaries
2.1 Main properties of $BV(\Omega )$ space
space
First of all let us introduce the space of functions of bounded variation, $BV(\Omega )$![]() , where $\Omega \subset \mathbb {R}^N$
, where $\Omega \subset \mathbb {R}^N$![]() is a domain. We say that $u \in BV(\Omega )$
is a domain. We say that $u \in BV(\Omega )$![]() , or is a function of bounded variation, if $u \in L^1(\Omega )$
, or is a function of bounded variation, if $u \in L^1(\Omega )$![]() , and its distributional derivative $Du$
, and its distributional derivative $Du$![]() is a vectorial Radon measure, i.e.,
is a vectorial Radon measure, i.e.,
It can be proved that $u \in BV(\Omega )$![]() if and only if $u \in L^1(\Omega )$
if and only if $u \in L^1(\Omega )$![]() and
and
The space $BV(\Omega )$![]() is a Banach space when endowed with the norm
is a Banach space when endowed with the norm
which is continuously embedded into $L^r(\Omega )$![]() for all $\displaystyle r \in [1,\,1^*]$
for all $\displaystyle r \in [1,\,1^*]$![]() , where ${1^* = N/(N-1)}$
, where ${1^* = N/(N-1)}$![]() . Since the domain $\Omega$
. Since the domain $\Omega$![]() is bounded, it holds also the compactness of the embeddings of $BV(\Omega )$
is bounded, it holds also the compactness of the embeddings of $BV(\Omega )$![]() into $L^r(\Omega )$
into $L^r(\Omega )$![]() for all $\displaystyle r \in [1,\,1^*)$
for all $\displaystyle r \in [1,\,1^*)$![]() .
.
The space $C^\infty (\overline {\Omega })$![]() is not dense in $BV(\Omega )$
is not dense in $BV(\Omega )$![]() with respect to the strong convergence. However, with respect to the strict convergence, it does. We say that $(u_n) \subset BV(\Omega )$
with respect to the strong convergence. However, with respect to the strict convergence, it does. We say that $(u_n) \subset BV(\Omega )$![]() converges to $u \in BV(\Omega )$
converges to $u \in BV(\Omega )$![]() in the sense of the strict convergence, if
in the sense of the strict convergence, if
and
as $n \to \infty$![]() . In [Reference Ambrosio, Fusco and Pallara6] one can see also that it is well defined a trace operator $BV(\Omega ) \hookrightarrow L^1(\partial \Omega )$
. In [Reference Ambrosio, Fusco and Pallara6] one can see also that it is well defined a trace operator $BV(\Omega ) \hookrightarrow L^1(\partial \Omega )$![]() , in such a way that
, in such a way that
is a norm equivalent to $\|\cdot \|_{BV}$![]() .
.
Given $u \in BV(\Omega )$![]() , we can decompose its distributional derivative as
, we can decompose its distributional derivative as
where $D^au$![]() is absolutely continuous with respect to the Lebesgue measure $\mathcal {L}^N$
is absolutely continuous with respect to the Lebesgue measure $\mathcal {L}^N$![]() , while $D^su$
, while $D^su$![]() is singular with respect to the same measure. Moreover, we denote the total variation of $Du$
is singular with respect to the same measure. Moreover, we denote the total variation of $Du$![]() , as $|Du|$
, as $|Du|$![]() .
.
In several arguments we use in this work, it is mandatory to have a sort of Green's Formula to expressions like $w \, \mbox {div}({\textbf z})$![]() , where ${\textbf z} \in L^\infty (\Omega,\,\mathbb {R}^N)$
, where ${\textbf z} \in L^\infty (\Omega,\,\mathbb {R}^N)$![]() , $\mbox {div}({\textbf z}) \in L^N(\Omega )$
, $\mbox {div}({\textbf z}) \in L^N(\Omega )$![]() and $w \in BV(\Omega )$
and $w \in BV(\Omega )$![]() . For this we have to somehow deal with the product between ${\textbf z}$
. For this we have to somehow deal with the product between ${\textbf z}$![]() and $Dw$
and $Dw$![]() , which we denote by $({\textbf z},\,Dw)$
, which we denote by $({\textbf z},\,Dw)$![]() . This can be done through the pairings theory, developed by Anzellotti in [Reference Anzellotti12] and independently by Frid and Chen in [Reference Chen and Frid19]. Below, we describe the main results of this theory.
. This can be done through the pairings theory, developed by Anzellotti in [Reference Anzellotti12] and independently by Frid and Chen in [Reference Chen and Frid19]. Below, we describe the main results of this theory.
Let us denote
For ${\textbf z} \in X_N(\Omega )$![]() and $w \in BV(\Omega )$
and $w \in BV(\Omega )$![]() , we define the distribution $({\textbf z},\,Dw) \in \mathcal {D}'(\Omega )$
, we define the distribution $({\textbf z},\,Dw) \in \mathcal {D}'(\Omega )$![]() as
as
for every $\varphi \in \mathcal {D}(\Omega )$![]() . With this definition, it can be proved that $({\textbf z},\,Dw)$
. With this definition, it can be proved that $({\textbf z},\,Dw)$![]() is in fact a Radon measure such that
is in fact a Radon measure such that
for every Borel set $B \subset \Omega$![]() .
.
In order to define an analogue of the Green's Formula, it is also necessary to describe a weak trace theory for ${\textbf z}$![]() . In fact, there exists a trace operator $[ \cdot,\, \nu ]: X_N(\Omega ) \to L^\infty (\partial \Omega )$
. In fact, there exists a trace operator $[ \cdot,\, \nu ]: X_N(\Omega ) \to L^\infty (\partial \Omega )$![]() such that
such that
and, if ${\textbf z} \in C^1(\overline {\Omega }_\delta,\,\mathbb {R}^N)$![]() ,
,
where by $\Omega _\delta$![]() we denote a $\delta$
we denote a $\delta$![]() -neighbourhood of $\partial \Omega$
-neighbourhood of $\partial \Omega$![]() . With these definitions, it can be proved that the following Green's Formula holds for every ${\textbf z} \in X_N(\Omega )$
. With these definitions, it can be proved that the following Green's Formula holds for every ${\textbf z} \in X_N(\Omega )$![]() and $w \in BV(\Omega )$
and $w \in BV(\Omega )$![]() ,
,
2.2 Nonlinear analysis on nondifferentiable functionals
In this subsection, for the reader's convenience, we recall some definitions and basic results on the critical point theory of locally Lipschitz continuous functionals (that is based on the subdifferential theory of Clarke [Reference Clarke20, Reference Clarke21]) as developed by Chang [Reference Chang17], Clarke [Reference Clarke20, Reference Clarke21] and Grossinho and Tersian [Reference Grossinho and Tersian26].
Let $E$![]() be a real Banach space. A functional $I:E \rightarrow {\mathbb {R}}$
be a real Banach space. A functional $I:E \rightarrow {\mathbb {R}}$![]() is locally Lipschitz continuous, $I \in Lip_{loc}(E,\, {\mathbb {R}})$
is locally Lipschitz continuous, $I \in Lip_{loc}(E,\, {\mathbb {R}})$![]() for short, if given $u \in E$
for short, if given $u \in E$![]() there is an open neighbourhood $V := V_u \subset E$
there is an open neighbourhood $V := V_u \subset E$![]() and some constant $M = M_V > 0$
and some constant $M = M_V > 0$![]() such that
such that
The directional derivative of $I$![]() at $u$
at $u$![]() in the direction of $v \in E$
in the direction of $v \in E$![]() is defined by
is defined by
Hence $I^0(u;.)$![]() is continuous, convex and its subdifferential at $z\in E$
is continuous, convex and its subdifferential at $z\in E$![]() is given by
is given by
where $\langle.,\,.\rangle$![]() is the duality pairing between $E^*$
is the duality pairing between $E^*$![]() and $E$
and $E$![]() . The generalized gradient of $I$
. The generalized gradient of $I$![]() at $u$
at $u$![]() is the set
is the set
Since $I^0(u;0) = 0$![]() , $\partial I(u)$
, $\partial I(u)$![]() is the subdifferential of $I^0(u;.)$
is the subdifferential of $I^0(u;.)$![]() in $0$
in $0$![]() .
.
It is also known that $\partial I(u)\subset E^*$![]() is convex, nonempty and weak*-compact and it is well defined
is convex, nonempty and weak*-compact and it is well defined
A critical point of $I$![]() is an element $u_\beta \in E$
is an element $u_\beta \in E$![]() such that $0\in \partial I(u_\beta )$
such that $0\in \partial I(u_\beta )$![]() and a critical value of $I$
and a critical value of $I$![]() is a real number $c$
is a real number $c$![]() such that $I(u_\beta )=c$
such that $I(u_\beta )=c$![]() for some critical point $u_\beta \in E$
for some critical point $u_\beta \in E$![]() .
.
We say that $I\in Lip_{loc}(E,\, \mathbb {R})$![]() satisfies the nonsmooth Palais–Smale condition at level $c\in \mathbb {R}$
satisfies the nonsmooth Palais–Smale condition at level $c\in \mathbb {R}$![]() (nonsmooth $(PS)_c$
(nonsmooth $(PS)_c$![]() -condition for short), if the following holds: every sequence $(u_n)\subset E$
-condition for short), if the following holds: every sequence $(u_n)\subset E$![]() , such that $I(u_n)\rightarrow c$
, such that $I(u_n)\rightarrow c$![]() and $\Lambda _I(u_n)\rightarrow 0$
and $\Lambda _I(u_n)\rightarrow 0$![]() has a strongly convergent subsequence.
has a strongly convergent subsequence.
Proposition 2.1 See [Reference Clarke20, Reference Clarke21, Reference Grossinho and Tersian26]
Let $I_1,\, I_2: E\rightarrow \mathbb {R}$![]() be locally Lipschitz functions, then:
be locally Lipschitz functions, then:
(i) $I_1+ I_2\in Lip_{loc}(E,\,\mathbb {R})$
 and $\partial (I_1+ I_2)(u) \subseteq \partial I_1(u) + \partial I_2(u),$
and $\partial (I_1+ I_2)(u) \subseteq \partial I_1(u) + \partial I_2(u),$ for all $u\in E.$
for all $u\in E.$
(ii) $\partial (\lambda I_1)(u) = \lambda \partial I_1(u)$
 for each $\lambda \in \mathbb {R},\, u\in E.$
for each $\lambda \in \mathbb {R},\, u\in E.$
(iii) Suppose that for each point $v$
 in a neighbourhood of $u,$
in a neighbourhood of $u,$ $I_1$
$I_1$ admits a Gateaux derivative $I_1'(v)$
admits a Gateaux derivative $I_1'(v)$ and that $I_1' :E\rightarrow E^*$
and that $I_1' :E\rightarrow E^*$ is continuous, then $\partial I_1(u) = \{I_1'(u)\}.$
is continuous, then $\partial I_1(u) = \{I_1'(u)\}.$
Theorem 2.2 See [Reference Clarke20, Reference Clarke21, Reference Grossinho and Tersian26]
Let $E$![]() be a Banach space and let $I\in Lip_{loc}(E,\,\mathbb {R})$
be a Banach space and let $I\in Lip_{loc}(E,\,\mathbb {R})$![]() with $I(0) = 0.$
with $I(0) = 0.$![]() Suppose there are numbers $\alpha,\,r>0$
Suppose there are numbers $\alpha,\,r>0$![]() and $e\in E,$
and $e\in E,$![]() such that
such that
(i) $I(u)\geq \alpha,$
 for all $u\in E; \|u\|=r,$
for all $u\in E; \|u\|=r,$
(ii) $I(e)<0$
 and $\|e\|>r.$
and $\|e\|>r.$
Let
Then $c\geq \alpha$![]() and there is a sequence $(u_{n})\subset E$
and there is a sequence $(u_{n})\subset E$![]() satisfying
satisfying
If, in addition, $I$![]() satisfies the nonsmooth $(PS)_c$
satisfies the nonsmooth $(PS)_c$![]() -condition, then $c$
-condition, then $c$![]() is a critical value of $I.$
is a critical value of $I.$![]()
3. Proof of theorem 1.1
In this section, to prove our main result, we will consider a family of auxiliary problems involving the p-Laplacian operator and discontinuous nonlinearity. We will use an approximation technique and variational methods for nondifferentiable functionals inspired by Molino-Segura de León [Reference Segura de León and Molino Salas32], Anzellotti-Frid-Chen [Reference Anzellotti12, Reference Chen and Frid19], Arcoya-Calahorrano [Reference Arcoya and Calahorrano13], Ambrosetti-Turner [Reference Ambrosetti and Turner5], Clarke [Reference Clarke20] and Chang [Reference Chang17].
In order to get such solutions of (1.1), the first step is to consider the problem

We say that $u_{p,\beta } \in W^{1,p}_0(\Omega )$![]() is a weak solution of (3.1), if there exists $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$
is a weak solution of (3.1), if there exists $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$![]() , such that
, such that
and it holds that, for almost every $x\in \Omega,$![]()

Inspired by Arcoya and Calahorrano [Reference Arcoya and Calahorrano13], which proved the existence of solution for a sublinear version of (3.1) (see also Ambrosetti and Turner [Reference Ambrosetti and Turner5]), we will use the nonsmooth critical point theory to prove that problem (3.1) has at least one solution $u_{p,\beta }\in W_0^{1,p}(\Omega )$![]() , which will be obtained by the nonsmooth version of the Mountain pass theorem (see theorem 2.2). Furthermore, we will prove some properties of this solution that will be useful to prove the existence of a solution to problem (1.1). To achieve this goal, first note that by Chang's results [Reference Chang17, theorem 2.1 and theorem 2.3], the functional $\mathcal {F}_\beta : L^q(\Omega )\rightarrow \mathbb {R}$
, which will be obtained by the nonsmooth version of the Mountain pass theorem (see theorem 2.2). Furthermore, we will prove some properties of this solution that will be useful to prove the existence of a solution to problem (1.1). To achieve this goal, first note that by Chang's results [Reference Chang17, theorem 2.1 and theorem 2.3], the functional $\mathcal {F}_\beta : L^q(\Omega )\rightarrow \mathbb {R}$![]() given by
given by
is locally Lipschitz and
where

It is clear that

The associated functional for (3.1) is $J_{p,\beta }: W_{0}^{1,p}(\Omega )\rightarrow \mathbb {R}$![]() , given by
, given by
Due to the presence of the Heaviside function $H,$![]() the functional $J_{p,\beta }$
the functional $J_{p,\beta }$![]() is not Fréchet differentiable, but is locally Lipschitz on $W_0^{1,p}(\Omega )$
is not Fréchet differentiable, but is locally Lipschitz on $W_0^{1,p}(\Omega )$![]() . Moreover, by [Reference Chang17, theorem 2.2] we have $\partial (\mathcal {F}_{H}\bigl |_{W_0^{1,p}})(u)=\partial \mathcal {F}_\beta (u),$
. Moreover, by [Reference Chang17, theorem 2.2] we have $\partial (\mathcal {F}_{H}\bigl |_{W_0^{1,p}})(u)=\partial \mathcal {F}_\beta (u),$![]() for all $u\in W_0^{1,p}(\Omega ).$
for all $u\in W_0^{1,p}(\Omega ).$![]() Hence, by proposition 2.1,
Hence, by proposition 2.1,
and therefore, by (3.4), (3.5) and (3.7), critical points of $J_{p,\beta },$![]() in the sense of the nonsmooth critical point theory, will give rise to solutions of (3.1).
in the sense of the nonsmooth critical point theory, will give rise to solutions of (3.1).
Since we want to find a nontrivial solution of (1.1) by using the solutions $u_{p,\beta }$![]() of (3.1) by passing to the limit as $p\rightarrow 1^+,$
of (3.1) by passing to the limit as $p\rightarrow 1^+,$![]() in what follows, we will consider $p\in (1,\,\overline {p})$
in what follows, we will consider $p\in (1,\,\overline {p})$![]() for some $\overline {p}\in (1,\,q)$
for some $\overline {p}\in (1,\,q)$![]() fixed.
fixed.
Lemma 3.1 For each $p\in (1,\,\overline {p})$![]() and $\beta >0,$
and $\beta >0,$![]() the functional $J_{p,\beta }$
the functional $J_{p,\beta }$![]() satisfies the geometric conditions of the Mountain pass theorem. More precisely,
satisfies the geometric conditions of the Mountain pass theorem. More precisely,
(i) There exist $r,\,\alpha >0,$
 which are independent of $\beta,$
which are independent of $\beta,$ such that $J_{p,\beta }(u)\geq \alpha$
such that $J_{p,\beta }(u)\geq \alpha$ for all $u\in W_0^{1,p}(\Omega )$
for all $u\in W_0^{1,p}(\Omega )$ with $\|u\|_{W_0^{1,p}(\Omega )}=r.$
with $\|u\|_{W_0^{1,p}(\Omega )}=r.$ Moreover, $\alpha$
Moreover, $\alpha$ can be chosen also independent of $p$
can be chosen also independent of $p$ .
.(ii) There exists $e = e(\beta )\in C_0^{\infty }(\Omega )$
 such that $J_{p,\beta }(e) < 0$
such that $J_{p,\beta }(e) < 0$ and $\|e\|_{W_0^{1,p}(\Omega )}> r.$
and $\|e\|_{W_0^{1,p}(\Omega )}> r.$
Proof. By Hölder's inequality,

Since, by [Reference Gilbarg and Trudinger25, proof of theorem 7.10], for each $u\in W_0^{1,p}(\Omega ),$![]()
we have,

where $C=\bigl (\overline {p}(N-1)/\sqrt {N}(N-\overline {p})\bigl )^{q}\max \{1,\,|\Omega |\}.$![]()
Note that

Then, by choosing $r=\biggl (\frac {1}{\overline {p}C+1}\biggl )^{\frac {1}{q-\overline {p}}}$ and $\alpha =r^{q}/\overline {p},$
and $\alpha =r^{q}/\overline {p},$![]() we conclude that $(i)$
we conclude that $(i)$![]() holds.
holds.
Now, let $\varphi \in C^{\infty }_0(\Omega )$![]() be such that $|\{\varphi >\beta \}|>0,$
be such that $|\{\varphi >\beta \}|>0,$![]() where $\{\varphi >\beta \}$
where $\{\varphi >\beta \}$![]() denotes the set $\{x\in \Omega : \varphi (x) > \beta \}.$
denotes the set $\{x\in \Omega : \varphi (x) > \beta \}.$![]() For each $t\geq 1,$
For each $t\geq 1,$![]() we get
we get

which implies in the existence of $e$![]() satisfying $(ii).$
satisfying $(ii).$![]()
Lemma 3.2 For each $p\in (1,\,\overline {p})$![]() and $\beta >0,$
and $\beta >0,$![]() $J_{p,\beta }$
$J_{p,\beta }$![]() satisfies the nonsmooth Palais–Smale condition.
satisfies the nonsmooth Palais–Smale condition.
Proof. Let $(u_n)\subset W_0^{1,p}(\Omega )$![]() be a $(PS)_c$
be a $(PS)_c$![]() sequence for $J_{p,\beta },$
sequence for $J_{p,\beta },$![]() that is, $J_{p,\beta }(u_n) \to c$
that is, $J_{p,\beta }(u_n) \to c$![]() and $\Lambda _{J_{p,\beta }}(u_{n})\rightarrow 0,$
and $\Lambda _{J_{p,\beta }}(u_{n})\rightarrow 0,$![]() where $\Lambda _{J_{p,\beta }}$
where $\Lambda _{J_{p,\beta }}$![]() is defined in (2.4). Hence, it follows from (2.4) and (3.7) that there exists $(\mu _{n})\subset \partial J_{p,\beta }(u_{n})$
is defined in (2.4). Hence, it follows from (2.4) and (3.7) that there exists $(\mu _{n})\subset \partial J_{p,\beta }(u_{n})$![]() such that
such that
where $\rho _{n}\in \partial \mathcal {F}_\beta (u_{n}).$![]() Then,
Then,

Moreover, note that by (3.3) and (3.4), we have
Hence,
which implies that the sequence $(u_n)$![]() is bounded in $W_0^{1,p}(\Omega )$
is bounded in $W_0^{1,p}(\Omega )$![]() . Thus, by Sobolev embedding theorems, passing to a subsequence if necessary, we obtain
. Thus, by Sobolev embedding theorems, passing to a subsequence if necessary, we obtain

Using a similar argument than [Reference Arcoya and Calahorrano13, pg. 1071], we conclude that $J_{p,\beta }$![]() satisfies the nonsmooth Palais–Smale condition.
satisfies the nonsmooth Palais–Smale condition.
Let us define the functional $I_{p,\beta }: W^{1,p}_0(\Omega ) \to \mathbb {R}$![]() , given by
, given by
Note that, by lemma 3.1, lemma 3.2 and theorem 2.2, $I_{p,\beta }$![]() has a critical point $u_{p,\beta } \in W_{0}^{1,p}(\Omega )$
has a critical point $u_{p,\beta } \in W_{0}^{1,p}(\Omega )$![]() at the level
at the level

that is,
Hence, there exists $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$![]() such that $u_{p,\beta }$
such that $u_{p,\beta }$![]() and $\rho _{p,\beta }$
and $\rho _{p,\beta }$![]() satisfy (3.2) and (3.3). Moreover, testing (3.2) with $\varphi = u_{p,\beta }^-:=\min \{u_{p,\beta },\,0\}$
satisfy (3.2) and (3.3). Moreover, testing (3.2) with $\varphi = u_{p,\beta }^-:=\min \{u_{p,\beta },\,0\}$![]() and using (3.3) we have $\|u^{-}_{p,\beta }\|^p_{W^{1,p}_0(\Omega )}=0,$
and using (3.3) we have $\|u^{-}_{p,\beta }\|^p_{W^{1,p}_0(\Omega )}=0,$![]() which implies that $u_{p,\beta }(x)\geq 0$
which implies that $u_{p,\beta }(x)\geq 0$![]() a.e. in $\Omega.$
a.e. in $\Omega.$![]()
Lemma 3.3 Let $u_{p,\beta }$![]() be given in (3.13). Then the family $(u_{p,\beta })_{1 < p < \overline {p}}$
be given in (3.13). Then the family $(u_{p,\beta })_{1 < p < \overline {p}}$![]() is bounded in $BV(\Omega ).$
is bounded in $BV(\Omega ).$![]()
Proof. By Young's inequality, we have
Hence, $I_{p,\beta }$![]() is nondecreasing with respect to $p$
is nondecreasing with respect to $p$![]() and arguing as in [Reference Segura de León and Molino Salas32], we conclude that $(I_{p,\beta }(u_{p,\beta }))_{1< p<\overline {p}}$
and arguing as in [Reference Segura de León and Molino Salas32], we conclude that $(I_{p,\beta }(u_{p,\beta }))_{1< p<\overline {p}}$![]() is increasing. Hence,
is increasing. Hence,
for all $1 < p_1\leq p_2.$![]() Note also that, by (3.13),
Note also that, by (3.13),

From (3.10) and (3.14), it follows that
where $C:=\frac {\overline {p}q}{q-\overline {p}}c_{\overline {p},\,\beta }>0$![]() is a constant independent of $p\in (1,\,\overline {p}).$
is a constant independent of $p\in (1,\,\overline {p}).$![]()
Applying once more Young's inequality, we obtain

for some constant $\overline {C}>0,$![]() independent of $p.$
independent of $p.$![]()
Lemma 3.4 For each $\beta >0,$![]() the function $u_{p,\beta }$
the function $u_{p,\beta }$![]() given in (3.13) satisfies
given in (3.13) satisfies
for some constant $\overline {C}>0$![]() independent of $p\in (1,\,\overline {p}).$
independent of $p\in (1,\,\overline {p}).$![]()
Proof. Here to simplify the notation we put $u=u_{p,\beta }$![]() and $\rho _{p,\beta }=\rho.$
and $\rho _{p,\beta }=\rho.$![]() To obtain the $L^\infty$
To obtain the $L^\infty$![]() -estimate we will use the Moser's iteration [Reference Moser31] and a careful analysis of some constants. For each $L>0$
-estimate we will use the Moser's iteration [Reference Moser31] and a careful analysis of some constants. For each $L>0$![]() , we define
, we define

with $\gamma >1$![]() to be determined later. Choosing $\varphi =z_{L,n}$
to be determined later. Choosing $\varphi =z_{L,n}$![]() in (3.2), we get
in (3.2), we get
Since
and $0\leq \rho (x)\leq |u(x)|^{q-1}$![]() for almost every $x\in \Omega,$
for almost every $x\in \Omega,$![]() see (3.3), we obtain
see (3.3), we obtain
On the other hand, by (3.8) it follows that
where $c_{p,\beta }=\bigl (p(N-1)/(N-p)\bigl )^{p}.$![]() Thus,
Thus,
hence, we get
Combining (3.17) and (3.18), we obtain
and so,
Now we use the Hölder's inequality (with exponents $p^*/(q-p)$![]() and $p^*/(p^*-(q-p))$
and $p^*/(p^*-(q-p))$![]() to get that
to get that

where $p<\frac {pp^*}{p^*-(q-p)}< p^*.$![]()
The previous inequality, (3.8) and (3.15) imply that

where

with the constant $C$![]() given in (3.15).
given in (3.15).
Using that $0\leq w_L=(uu_L^{\gamma -1})\leq u^{\gamma }$![]() on the right-hand side of (3.19) and then letting $L\rightarrow \infty$
on the right-hand side of (3.19) and then letting $L\rightarrow \infty$![]() on the left-hand side, as a consequence of Fatou's Lemma on the variable $L$
on the left-hand side, as a consequence of Fatou's Lemma on the variable $L$![]() , we have
, we have

from which we get that
Let us define $\sigma :=p^*/\alpha ^*.$![]() When $\gamma =\sigma$
When $\gamma =\sigma$![]() in (3.21), since $\gamma \alpha ^*=p^*$
in (3.21), since $\gamma \alpha ^*=p^*$![]() we have $u\in L^{p^*\sigma }(\Omega )$
we have $u\in L^{p^*\sigma }(\Omega )$![]() and
and
Now, choosing $\gamma =\sigma ^2$![]() in (3.21), since $\gamma \alpha ^*=p^*\sigma$
in (3.21), since $\gamma \alpha ^*=p^*\sigma$![]() and $p^*\gamma =p^*\sigma ^2,$
and $p^*\gamma =p^*\sigma ^2,$![]() we obtain
we obtain
by using (3.22) and (3.23), we have
For $n\geq 1,$![]() we define $\sigma _n$
we define $\sigma _n$![]() inductively so that $\sigma _n=\sigma ^n.$
inductively so that $\sigma _n=\sigma ^n.$![]() Then, from (3.21), it follows that
Then, from (3.21), it follows that
Note that

Thus, since $\sigma >1,$![]() passing to the limit as $n\rightarrow \infty$
passing to the limit as $n\rightarrow \infty$![]() in (3.24) we conclude that $u\in L^{\infty }(\Omega )$
in (3.24) we conclude that $u\in L^{\infty }(\Omega )$![]() and
and
Finally, since $\sigma =\frac {N}{N-p}-\frac {q}{p}+1$![]() and $1< p< q<1^*< p^*,$
and $1< p< q<1^*< p^*,$![]() using once more (3.8), the expression of $\theta _p$
using once more (3.8), the expression of $\theta _p$![]() (see (3.20)) and (3.25) we conclude the proof of the lemma.
(see (3.20)) and (3.25) we conclude the proof of the lemma.
As a consequence of lemma 3.3 and the compactness of the embedding $BV(\Omega )\hookrightarrow L^r(\Omega )$![]() , for $r\in [1,\,1^*)$
, for $r\in [1,\,1^*)$![]() (where $1^* := N/(N-1)$
(where $1^* := N/(N-1)$![]() ), it follows that there exists $u_\beta \in BV(\Omega )$
), it follows that there exists $u_\beta \in BV(\Omega )$![]() such that, as $p \to 1^+,$
such that, as $p \to 1^+,$![]()
and
Hence, according to lemma 3.4 we have $u_\beta \in L^\infty (\Omega )$![]() and $u_\beta (x)\geq 0$
and $u_\beta (x)\geq 0$![]() for almost every $x\in \Omega.$
for almost every $x\in \Omega.$![]()
In what follows, we will prove that $u_\beta$![]() is a solution of (1.1), in the sense of definition (1.2). Furthermore, we will prove that $u_\beta \not \equiv 0.$
is a solution of (1.1), in the sense of definition (1.2). Furthermore, we will prove that $u_\beta \not \equiv 0.$![]()
We start with the following result:
Lemma 3.5 Let $u_{p,\beta } \in W^{1,p}_0(\Omega ),$![]() $\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$
$\rho _{p,\beta } \in L^{\frac {q}{q-1}}(\Omega )$![]() and $u_\beta \in BV(\Omega )$
and $u_\beta \in BV(\Omega )$![]() satisfying (3.2), (3.3) and (3.26). Then, there exists $\rho _{\beta } \in L^{\frac {q}{q-1}}(\Omega ),$
satisfying (3.2), (3.3) and (3.26). Then, there exists $\rho _{\beta } \in L^{\frac {q}{q-1}}(\Omega ),$![]() such that
such that
Moreover, $\rho _{\beta }$![]() satisfies, for almost every $x\in \Omega,$
satisfies, for almost every $x\in \Omega,$![]()

Proof. By lemma 3.4, it follows that $(\rho _{p,\beta })_{1 < p < \overline {p}}$![]() is bounded in $L^{\frac {q}{q-1}}(\Omega )$
is bounded in $L^{\frac {q}{q-1}}(\Omega )$![]() . Hence, there exists $\rho _{\beta } \in L^{\frac {q}{q-1}}(\Omega )$
. Hence, there exists $\rho _{\beta } \in L^{\frac {q}{q-1}}(\Omega )$![]() , such that (3.28) holds. Moreover, if $E \subset \Omega$
, such that (3.28) holds. Moreover, if $E \subset \Omega$![]() is a measurable set, then
is a measurable set, then
Now, let us show that $\rho _\beta$![]() satisfies (3.29). First of all, note that
satisfies (3.29). First of all, note that
Indeed, otherwise, a measurable set $E \subset \Omega$![]() would exist, such that $\rho _\beta (x) < 0$
would exist, such that $\rho _\beta (x) < 0$![]() , in $E$
, in $E$![]() . Then,
. Then,
Hence, from (3.30), we have a contradiction with the fact that $\rho _{p,\beta }(x) \geq 0$![]() , for all $p > 1$
, for all $p > 1$![]() .
.
Now let us show that
Let $E = [u_\beta < \beta ]$![]() and note that
and note that

Claim 1: $\displaystyle \int _{E \cap [u_{p,\beta } \geq \beta ]}u_{p,\beta }^{q-1} \,{\rm d}x = o_p(1)$![]() .
.
Assuming for a while that claim 1 holds true, then from (3.30), (3.31) and (3.33), it follows that (3.32) holds.
Now, let us show that the claim holds. First of all, let us show that
Indeed, let us suppose by contradiction that there exists $E^* \subset E$![]() with positive measure such that, for every fixed $x \in E^*$
with positive measure such that, for every fixed $x \in E^*$![]() , there exists $(p_{n,x})_{n \in \mathbb {N}}$
, there exists $(p_{n,x})_{n \in \mathbb {N}}$![]() , such that $p_{n,x} \to 1^+$
, such that $p_{n,x} \to 1^+$![]() , as $n \to +\infty$
, as $n \to +\infty$![]() and
and
This, in turn, is equivalent to
By doing $n \to +\infty$![]() in (3.35), since $p_{n,x} \to 1^+$
in (3.35), since $p_{n,x} \to 1^+$![]() , we have that
, we have that
But this contradicts the fact that $E^* \subset E$![]() . Hence (3.34) holds.
. Hence (3.34) holds.
Therefore, from (3.34) and the Lebesgue Convergence Theorem, it follows that claim 1 holds.
Now let us show that
For this, let us define $E = [u_\beta > \beta ]$![]() . Note that
. Note that
As in (3.34), we can prove that
Then, from (3.38) and Lebesgue Convergence Theorem,
On the other hand, since
we have from (3.26) and the fact that $\chi _{[u_{p,\beta } > \beta ]} \to 1$![]() , a.e. in $E$
, a.e. in $E$![]() , as $p \to 1^+$
, as $p \to 1^+$![]() , that
, that
Then, from (3.37), (3.39) and (3.40), it follows that
Hence, from (3.30) and (3.41), we have that
Claim 2: $\rho _\beta (x) \leq u_\beta ^{q-1}(x)$![]() in $[u_\beta \geq \beta ]$
in $[u_\beta \geq \beta ]$![]() .
.
Assuming that claim 2 holds, it follows from (3.42) that
and
and we are done.
In order to prove claim 2, let us assume by contradiction that there exists $E_* \subset [u_\beta \geq \beta ]$![]() , with positive measure and such that
, with positive measure and such that
Then,
Then, from (3.26) and (3.30), there exists $p_n \to 1^+$![]() , as $n \to +\infty$
, as $n \to +\infty$![]() , such that
, such that
which contradicts the fact that $\rho _{p,\beta }(x) \leq u_{p,\beta }^{q-1}(x)$![]() , a.e. in $\Omega$
, a.e. in $\Omega$![]() .
.
Then claim 2 holds and this finishes the proof.
Lemma 3.6 For each $\beta >0,$![]() there exists a vector field $\textbf {z}_{\beta } \in L^\infty (\Omega,\,\mathbb {R}^N)$
there exists a vector field $\textbf {z}_{\beta } \in L^\infty (\Omega,\,\mathbb {R}^N)$![]() such that $\|\textbf {z}_{\beta }\|_\infty \leq 1$
such that $\|\textbf {z}_{\beta }\|_\infty \leq 1$![]() and
and
with $\rho _{\beta }$![]() satisfying (3.29).
satisfying (3.29).
Proof. The inequality (3.15) implies that (see [Reference Andreu, Ballester, Caselles and Mazón8, proposition 3] or [Reference Mercaldo, Rossi, Segura de León and Trombetti29, theorem 3.3]) there exists $\textbf {z}_{\beta } \in L^\infty (\Omega,\,\mathbb {R}^N)$![]() , such that $\|\textbf {z}_{\beta }\|_\infty \leq 1$
, such that $\|\textbf {z}_{\beta }\|_\infty \leq 1$![]() and
and
for all $1 \leq r < \infty$![]() . In particular, as $p \to 1^+$
. In particular, as $p \to 1^+$![]() ,
,
Therefore, by using (3.2), (3.28) and (3.46) and the Lebesgue dominated convergence theorem, we conclude that
which proves the lemma.
Lemma 3.7 The function $u_\beta$![]() and the vector field $\textbf {z}_{\beta }$
and the vector field $\textbf {z}_{\beta }$![]() satisfy the following equality in the sense of measures in $\Omega,$
satisfy the following equality in the sense of measures in $\Omega,$![]()
Proof. First of all, since $\|\textbf {z}_{\beta }\|_\infty \leq 1$![]() , it follows that, $(\textbf {z}_{\beta },\,Du_\beta ) \leq |Du_\beta |$
, it follows that, $(\textbf {z}_{\beta },\,Du_\beta ) \leq |Du_\beta |$![]() in $\mathcal {M}(\Omega )$
in $\mathcal {M}(\Omega )$![]() . In fact, for any Borel set $B$
. In fact, for any Borel set $B$![]() , by (2.1),
, by (2.1),

Hence, it is enough to show the opposite inequality, i.e., that for all $\varphi \in C^1_0(\Omega )$![]() , $\varphi \geq 0$
, $\varphi \geq 0$![]() ,
,
In order to do so, let us consider $u_{p,\beta } \varphi \in W^{1,p}(\Omega )$![]() as a test function in (3.1). Thus we obtain,
as a test function in (3.1). Thus we obtain,
Now we shall calculate the lower limit as $p \to 1^+$![]() in both sides of (3.48). Before it, note that, Young's inequality and the lower semicontinuity of the map $v \mapsto \displaystyle \int _\Omega \varphi |Dv|$
in both sides of (3.48). Before it, note that, Young's inequality and the lower semicontinuity of the map $v \mapsto \displaystyle \int _\Omega \varphi |Dv|$![]() with respect to the $L^r(\Omega )$
with respect to the $L^r(\Omega )$![]() convergence, imply that
convergence, imply that

Moreover, by (3.46), it follows that
Finally, Lebesgue's dominated convergence theorem and (3.26) imply that
Then, from (3.44), (3.48), (3.49) and (3.50), it follows that

Then, (3.47) holds and this finishes the proof.
Lemma 3.8 The function $u_\beta$![]() satisfies $[\textbf {z}_{\beta },\,\nu ] \in \mbox {sign}(-u_\beta )$
satisfies $[\textbf {z}_{\beta },\,\nu ] \in \mbox {sign}(-u_\beta )$![]() on $\partial \Omega$
on $\partial \Omega$![]() .
.
Proof. To check that $[\textbf {z}_{\beta },\,\nu ]\in sign(-u_\beta )$![]() it is enough to show that
it is enough to show that
Indeed, since
the integrand in (4.18) is nonnegative. Then, (4.18) holds if and only if $[\textbf {z}_{\beta },\,\nu ](-u_\beta ) = |u_\beta |$![]() $\mathcal {H}^{N-1}$
$\mathcal {H}^{N-1}$![]() a.e. on $\partial \Omega$
a.e. on $\partial \Omega$![]() .
.
In order to verify (4.18), let us consider $(u_{p,\beta } - \varphi ) \in W^{1,p}_{0}(\Omega )$![]() as test function in (3.1) with $\varphi \in C^1_{0}(\Omega )$
as test function in (3.1) with $\varphi \in C^1_{0}(\Omega )$![]() . Then we get
. Then we get
From Young's inequality, Green's Formula, (3.44), (3.46), lemma 3.7 and (3.52), we have that, as $p \to 1^+$![]() ,
,

Hence, from (3.53) and the lower semicontinuity of the norm in $BV(\Omega )$![]() , it follows that
, it follows that
But the last inequality implies in (4.18) and we are done.
Now, let us prove that the function $u_\beta \in BV(\Omega )\cap L^\infty (\Omega )$![]() is a nonnegative and nontrivial solution of (1.1), in the sense of the definition (1.2).
is a nonnegative and nontrivial solution of (1.1), in the sense of the definition (1.2).
First of all, note that by lemmas 3.6, 3.7 and 3.8, $u_\beta \in BV(\Omega ),$![]() $\rho _{\beta }\in L^{\frac {q}{q-1}}(\Omega )$
$\rho _{\beta }\in L^{\frac {q}{q-1}}(\Omega )$![]() and $\textbf {z}_{\beta }\in L^{\infty }(\Omega,\,\mathbb {R}^N)$
and $\textbf {z}_{\beta }\in L^{\infty }(\Omega,\,\mathbb {R}^N)$![]() satisfy (1.2) and (1.3). Moreover, since $u_{p,\beta }(x)\geq 0$
satisfy (1.2) and (1.3). Moreover, since $u_{p,\beta }(x)\geq 0$![]() for almost every $x\in \Omega,$
for almost every $x\in \Omega,$![]() according to (3.27) and lemma 3.4, it follows that $u_\beta \in L^{\infty }(\Omega )$
according to (3.27) and lemma 3.4, it follows that $u_\beta \in L^{\infty }(\Omega )$![]() and $u_\beta (x)\geq 0$
and $u_\beta (x)\geq 0$![]() for almost every $x\in \Omega.$
for almost every $x\in \Omega.$![]()
Now let us show that $u_\beta \not \equiv 0.$![]() Invoking lemma 3.1 and (3.13), we have
Invoking lemma 3.1 and (3.13), we have
Hence, since $\alpha$![]() is independent of $p$
is independent of $p$![]() (see lemma 3.1), (3.2), (3.26), (3.28), and Lebesgue's dominated convergence theorem, imply that
(see lemma 3.1), (3.2), (3.26), (3.28), and Lebesgue's dominated convergence theorem, imply that
Thus, combining (3.44), Green's Formula (see (2.3)), lemma 3.7, lemma 3.8 and (3.56), we deduce that

thus $u_\beta \not \equiv 0$![]() . Then theorem 1.1 is proved.
. Then theorem 1.1 is proved.
4. Proof of theorem 1.2
Now, let us perform a deep analysis of the behaviour of $u_{p,\beta }$![]() , as $\beta \to 0^+$
, as $\beta \to 0^+$![]() .
.
For each $\beta > 0$![]() , let us define the functional $I_\beta : BV(\Omega ) \to \mathbb {R}$
, let us define the functional $I_\beta : BV(\Omega ) \to \mathbb {R}$![]() , given by
, given by
Note that, since ${\bf z}_{\beta }$![]() and $u_\beta$
and $u_\beta$![]() satisfy
satisfy

by taking $u_\beta$![]() as test function in (4.1) and using Green's Formula, (3.1) and (3.28), it follows that
as test function in (4.1) and using Green's Formula, (3.1) and (3.28), it follows that

Moreover, from (3.26) and (3.27), it follows that
Hence, from (4.2) and (4.3), we have that
Since we are interested in the behaviour of $u_\beta$![]() , as $\beta \to 0^+$
, as $\beta \to 0^+$![]() , let us assume from now on that $0 < \beta < \beta _0$
, let us assume from now on that $0 < \beta < \beta _0$![]() .
.
Lemma 4.1 The family $(u_\beta )_{0 < \beta < \beta _0}$![]() is bounded in $BV(\Omega )$
is bounded in $BV(\Omega )$![]() .
.
Proof. First of all, let us prove that, if $0 < \beta _1 < \beta _2 < \beta _0$![]() , then
, then
In order to do so, let us prove that, for $p > 1$![]() fixed,
fixed,
Note that, for $u \in W^{1,p}_0(\Omega )$![]() , since $F_{\beta _1}(u) \geq F_{\beta _2}(u)$
, since $F_{\beta _1}(u) \geq F_{\beta _2}(u)$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() , it follows that
, it follows that
Moreover, let us assume that the function $e$![]() in lemma 3.1, is $e(\beta _0)$
in lemma 3.1, is $e(\beta _0)$![]() , i.e., that satisfies $I_{p,\beta _0}(e) < p/(p-1)$
, i.e., that satisfies $I_{p,\beta _0}(e) < p/(p-1)$![]() . Hence, from (4.7), we have that
. Hence, from (4.7), we have that
for all $0 < \beta < \beta _0$![]() . Hence, in the definition of $c_{p,\beta }$
. Hence, in the definition of $c_{p,\beta }$![]() , for $0 < \beta < \beta _0$
, for $0 < \beta < \beta _0$![]() , we can assume without loss of generality that $e = e(\beta _0)$
, we can assume without loss of generality that $e = e(\beta _0)$![]() and then the class of paths $\Gamma$
and then the class of paths $\Gamma$![]() does not depend on $\beta$
does not depend on $\beta$![]() . Then, from (4.7), it follows that
. Then, from (4.7), it follows that

This, in turn, proves (4.6).
Hence, from (4.4), passing the limit as $p \to 1^+$![]() in (4.6), we have that (4.5) holds.
in (4.6), we have that (4.5) holds.
Then, for all $0 < \beta < \beta _0$![]() ,
,
Note that, by using $u_\beta$![]() as test function in (4.1), from Green's Formula, we have that
as test function in (4.1), from Green's Formula, we have that

Then, from (3.29), (4.8) and the definition of $F_\beta$![]() , we have that
, we have that

Hence, since $(I_\beta (u_{\beta }))_{0 < \beta < \beta _0}$![]() is bounded, it follows from the last inequality that $(u_\beta )_{0 < \beta < \beta _0}$
is bounded, it follows from the last inequality that $(u_\beta )_{0 < \beta < \beta _0}$![]() is also bounded.
is also bounded.
From the last result, there exists $u_0 \in BV(\Omega )$![]() such that, for all $r \in [1,\,1^*)$
such that, for all $r \in [1,\,1^*)$![]() ,
,
and
Moreover, note that the boundedness on $(u_\beta )_{0 < \beta < \beta _0}$![]() and (3.29) implies also that $(\rho _\beta )_{0 < \beta < \beta _0}$
and (3.29) implies also that $(\rho _\beta )_{0 < \beta < \beta _0}$![]() is bounded in $L^\frac {q}{q-1}(\Omega )$
is bounded in $L^\frac {q}{q-1}(\Omega )$![]() . Then, as in lemma 3.5, it is possible to show that there exists $\rho _0 \in L^\frac {q}{q-1}(\Omega )$
. Then, as in lemma 3.5, it is possible to show that there exists $\rho _0 \in L^\frac {q}{q-1}(\Omega )$![]() , such that
, such that
and
Now, let us deal with the family of vector fields $({\bf z}_\beta )_{0 < \beta < \beta _0}$![]() . Note that, since $\|{\bf z}_\beta \|_\infty \leq 1$
. Note that, since $\|{\bf z}_\beta \|_\infty \leq 1$![]() for all $\beta \in (0,\,\beta _0)$
for all $\beta \in (0,\,\beta _0)$![]() , then there exists ${\bf z}_0 \in L^\infty (\Omega,\,\mathbb {R}^N)$
, then there exists ${\bf z}_0 \in L^\infty (\Omega,\,\mathbb {R}^N)$![]() , such that
, such that
This, on the other hand, implies that ${\bf z}_\beta \rightharpoonup {\bf z}_0$![]() in $L^1(\Omega,\,\mathbb {R}^N)$
in $L^1(\Omega,\,\mathbb {R}^N)$![]() , i.e., for all $\psi \in L^\infty (\Omega,\,\mathbb {R}^N)$
, i.e., for all $\psi \in L^\infty (\Omega,\,\mathbb {R}^N)$![]() ,
,
For every $\varphi \in C^\infty _c(\Omega )$![]() , since $\nabla \varphi \in L^\infty (\Omega,\,\mathbb {R}^N)$
, since $\nabla \varphi \in L^\infty (\Omega,\,\mathbb {R}^N)$![]() , by (4.15), we have that
, by (4.15), we have that
from where it follows that
Hence, from (4.11) and (4.16), we have that
Lemma 4.2 The function $u_0$![]() and the vector field ${\bf z}_0\!$
and the vector field ${\bf z}_0\!$![]() satisfy the following equality,
satisfy the following equality,
Proof. First of all, note that, from (2.1),
For the inverse inequality, let $\varphi \in \mathcal {D}(\Omega )$![]() , $\varphi \geq 0$
, $\varphi \geq 0$![]() . In (4.1), let us take $\varphi u_\beta$
. In (4.1), let us take $\varphi u_\beta$![]() as test function in (4.1). Then,
as test function in (4.1). Then,
Taking into account that $({\bf z}_\beta,\,Du_\beta ) = |Du_\beta |$![]() in $\mathcal {M}(\Omega )$
in $\mathcal {M}(\Omega )$![]() ,
,
Taking the $\liminf$![]() as $\beta \to 0^+$
as $\beta \to 0^+$![]() , from the lower semicontinuity of the norm in $BV(\Omega )$
, from the lower semicontinuity of the norm in $BV(\Omega )$![]() with respect to the $L^r$
with respect to the $L^r$![]() convergence, (4.9), (4.11) and (4.16), it follows that
convergence, (4.9), (4.11) and (4.16), it follows that

This, in turn, proves that $|Du_0| \leq ({\bf z}_0,\,Du_0)$![]() and this finishes the proof.
and this finishes the proof.
Lemma 4.3 The function $u_0$![]() satisfies $[\textbf {z}_0,\,\nu ] \in \mbox {sign}(-u_0)$
satisfies $[\textbf {z}_0,\,\nu ] \in \mbox {sign}(-u_0)$![]() on $\partial \Omega$
on $\partial \Omega$![]() .
.
Proof. As in lemma 3.8, it is enough to show that
In order to verify (4.18), let us consider $(u_\beta - \varphi ) \in BV(\Omega )\cap L^\infty (\Omega )$![]() as test function in (4.1), where $\varphi \in \mathcal {D}(\Omega )$
as test function in (4.1), where $\varphi \in \mathcal {D}(\Omega )$![]() . Then, from (2.3) and (4.1), we get
. Then, from (2.3) and (4.1), we get

Then, calculating the $\liminf$![]() in (4.19), from the lower semicontinuity of the norm in $BV(\Omega )$
in (4.19), from the lower semicontinuity of the norm in $BV(\Omega )$![]() , (4.17) and lemma 4.2, we have that
, (4.17) and lemma 4.2, we have that

From the last inequality, it follows that
Since the inverse inequality is trivial, it follows that (4.18) holds.
Then, from (4.17) and lemmas 4.2 and 4.3, it follows that $u_0$![]() is a solution of (1.4).
is a solution of (1.4).
Now, in order to end up the proof of theorem 1.2, let us show that there exist constants $\mu,\, \beta _{0} > 0$![]() , such that
, such that
From (3.55) it follows that
where $\alpha$![]() is independent of $\beta$
is independent of $\beta$![]() and $p\in (1,\, \overline {p})$
and $p\in (1,\, \overline {p})$![]() . Since $\rho _{p,\beta }$
. Since $\rho _{p,\beta }$![]() verifies (3.3),
verifies (3.3),
for all $\beta >0$![]() and $p\in (1,\, \overline {p})$
and $p\in (1,\, \overline {p})$![]() . To conclude the proof, it is enough to prove that
. To conclude the proof, it is enough to prove that
In fact, if (4.22) holds true, then from (3.26), passing to the upper limit as $p\to 1^+$![]() in (4.21), we get
in (4.21), we get
for all $\beta >0$![]() . Now, suppose by contradiction that there exists a subsequence $\beta _{n}\to 0$
. Now, suppose by contradiction that there exists a subsequence $\beta _{n}\to 0$![]() such that
such that
Since, by (4.23), we have
it follows from Hölder's inequality that

for some $q< r< N/(N-1)$![]() . Then, (4.24) and (4.25) would lead us to a contradiction.
. Then, (4.24) and (4.25) would lead us to a contradiction.
Hence, to conclude the proof, it remains us to show (4.22). For this purpose, observe that

Moreover, since
it follows from (3.26), (4.26), (4.27) and Lebesgue's dominated convergence theorem, that (4.22) holds true.
To conclude that $u_0$![]() is nontrivial, note that by (4.23), $u_0\geq 0$
is nontrivial, note that by (4.23), $u_0\geq 0$![]() and Lebesgue's dominated convergence theorem,
and Lebesgue's dominated convergence theorem,
then, $u_0\not \equiv 0.$![]() Finally, since $\rho _\beta (x)\in [\underline {f}_\beta (u_\beta (x)),\,\overline {f}_\beta (u_\beta (x))],$
Finally, since $\rho _\beta (x)\in [\underline {f}_\beta (u_\beta (x)),\,\overline {f}_\beta (u_\beta (x))],$![]() by (3.5), (4.9) and (4.12), we conclude that $\rho _0(x)=u_0(x)^{q-1}$
by (3.5), (4.9) and (4.12), we conclude that $\rho _0(x)=u_0(x)^{q-1}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() and therefore $u_0$
and therefore $u_0$![]() is solution of the continuous problem (1.4).
is solution of the continuous problem (1.4).
Acknowledgments
Marcos T.O. Pimenta is partially supported by FAPESP 2021/04158-4, CNPq 303788/2018-6 and FAPDF, Brazil. J. R. Santos Júnior is partially supported by FAPESP 2021/10791-1 and CNPq 313766/2021-5, Brazil.