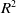Nomenclature
Abbreviations
- VSV
-
variable stator vanes
- MLKG
-
multi-layer Kriging surrogate
- KG
-
Kriging model
- MSE
-
mean squared error
- R 2
-
R square
- RAVSV
-
reliability analysis of vane stator variables
- KPLS
-
Kriging surrogate with partial least squares
- MIC
-
maximal information coefficient
- KMIC
-
Kriging surrogate with maximal information coefficient
- HDKM-PCDR
-
high-dimensional Kriging modeling method through principal component dimension reduction
Symbols
-
 $\boldsymbol{x}$
$\boldsymbol{x}$
-
input data
-
 $\hat y\left( \boldsymbol{x} \right)$
$\hat y\left( \boldsymbol{x} \right)$
-
the unknown function of interest
-
 $\boldsymbol{f}\left( \boldsymbol{x} \right)$
$\boldsymbol{f}\left( \boldsymbol{x} \right)$
-
the regression models of KG
-
 $\boldsymbol\beta $
$\boldsymbol\beta $
-
the unknown parameters of KG
-
 $\boldsymbol{Z}\left( \boldsymbol{x} \right)$
$\boldsymbol{Z}\left( \boldsymbol{x} \right)$
-
the random variables in KG
-
 $\sigma $
$\sigma $
-
standard deviation of input samples
-
 $\boldsymbol{R}\left( {{\boldsymbol{x}_i},{\boldsymbol{x}_j}} \right)$
$\boldsymbol{R}\left( {{\boldsymbol{x}_i},{\boldsymbol{x}_j}} \right)$
-
the correlation models of KG
-
 ${\hat y^{\left( p \right)}}\left( \boldsymbol{x} \right)$
${\hat y^{\left( p \right)}}\left( \boldsymbol{x} \right)$
-
the output response of p-th object
-
 ${x^{\left( p \right)}}$
${x^{\left( p \right)}}$
-
the input parameter of the p-th object
-
 $\boldsymbol{erro}{\boldsymbol{r}_{\boldsymbol{i,j}}}$
$\boldsymbol{erro}{\boldsymbol{r}_{\boldsymbol{i,j}}}$
-
the error of surrogate model
- A
-
the maximum fitting error of all samples
-
 ${c_{l,j}}$
${c_{l,j}}$
-
constant number
-
 $Vary_{j,p}^l{\rm{\;}}$
$Vary_{j,p}^l{\rm{\;}}$
-
the variance of
 $y_{j,p}^l$
.
$y_{j,p}^l$
.
1.0 Introduction
The variable cycle engine is a new-generation aircraft engine that achieves different thermodynamic cycles by altering specific engine components’ geometric shapes, dimensions or positions [Reference Zhang, Liu and Liu1]. The variable stator vanes (VSV) are a set of typical spatial linkage mechanisms widely used in the variable cycle engine compressor (Fig. 1) [Reference Wang, Li, Fan and Li2]. Their role is to expand the compressor’s operating range and provide the engine with a greater surge margin. The reliability of VSV directly affects the overall performance of the aero-engines. For example, in the operating process of the VSV, the reciprocating motion of multiple rocker arms frequently causes random high-frequency alternating stress and high cycle fatigue (HCF) failure. It is worth highlighting that the HCF failure of multiple rocker arms has emerged as the predominant failure mode in aero-engines. Many scholars have researched VSV failures to improve the engine’s reliability. Michael [Reference Michael3] studied the motion process of VSV in a homogeneous coordinate system and derived the motion equation. Peng [Reference Peng4] studied the effect of the circumferential misalignment angle of the VSV on the rotational stall of the engine. Zhang [Reference Zhang5] conducted kinematic and dynamic simulation analysis on the simplified VSV, considering the influence of factors such as rocker arm flexibility, motion pair friction and load. Despite these efforts, research on VSV primarily focuses on motion simulation under deterministic conditions, with limited attention to reliability under geometric and load uncertainties. The reason is that the reliability analysis of VSV is a complex task due to the involvement of multiple components (Fig. 2) and high dimensionality input [Reference Xie, Jia and Yuan6]. These difficulties result in time-consuming motion solving for VSV reliability.

Figure 1. The vane stator variables.

Figure 2. VSV contains more than 30 objects and 64 random variables.
Bai [Reference Zhang, Song and Bai7] studied the reliability of a simplified VSV by using surrogate model technique. Surrogate model, which replaces motion solving, is a common approach for reliability analysis [Reference Zhu8–Reference Huang and Du10]. They can greatly improve the design efficiency for high-fidelity but computationally expensive models [Reference Gao, Chen and Yi11–Reference Bhosekar and Ierapetritou14]. However, surrogate models suffer from well-known drawbacks in multiple components and high-dimension problems. The first drawback is that the covariance matrix of the surrogate model may increase dramatically if the model requires a large number of sample points. As a result, inverting the covariance matrix is computationally expensive. The second drawback is that optimising the subproblem involves estimating the hyperparameters for the covariance matrix [Reference Li, Wang and Jia15, Reference Li and Shi16]. Unfortunately, high-dimensional input is often unavoidable in the reliability analysis of vane stator variables [Reference Han, Song, Han and Wang17, Reference Hu, Rui, Gao, Gou and Gong18].
To address high-dimensional difficulties in the reliability analysis of VSV, dimensionality reduction methods have to be used prior to surrogate models [Reference Zhou and Lu19, Reference Deng20]. The common dimensionality reduction [Reference Li and Shi16, Reference Lataniotis, Marelli and Sudret21–Reference Dai, Ding and Wang25] techniques rank the input variables with their contribution to the model response and remove those input variables with less contribution. A popular branch of dimensionality reduction called global sensitivity analysis focuses on contributing to the output from the entire input range [Reference Cheng, Lu, Zhou, Shi and Wei26, Reference Borgonovo, Apostolakis, Tarantola and Saltelli27]. Calculating the global sensitivity analysis requires the evaluation of multi-dimensional integrals over the input space of the simulator. Even if the dimensionality reduction method is adopted, many design parameters still need to be considered in VSV [Reference Tripathy and Bilionis28]. Due to the above shortcomings, the common surrogate model can hardly be applied to VSV reliability [Reference Lataniotis, Marelli and Sudret21, Reference Guo, Mahadevan and Matsumoto22]. Besides, VSV is a typical hierarchical structure, where motion is influenced by the lower-level structure. Existing surrogate models only focus on the relationship between inputs and final outputs, lacking a description of the connections between intermediate structures. For structures with such hierarchical relationships, the prediction accuracy of existing surrogate models is insufficient, making them unsuitable for reliability calculations of VSV mechanisms. This is a significant reason for the limited research on the reliability of VSV mechanisms. Hence, there’s an urgent need to develop precise and efficient reliability analysis methodologies tailored for VSV.
In this case, to improve the computing accuracy and efficiency of VSV reliability, a multi-layer Kriging surrogate (MLKG) is proposed in this paper. The MLKG is a combination of multiple Kriging (KG) surrogate models that are arranged in a hierarchical structure, where each layer represents a different level of abstraction. By breaking the reliability analysis of VSV down into smaller problems, MLKG decomposes the large surrogate model and reduces the input dimension of sub-layer Kriging model. In this way, the MLKG can capture the complex interactions between the inputs and outputs of the problem, while maintaining a high degree of accuracy and efficiency. For some complex assemblies, there may be a lot of layers that can be decomposed, and may lead to a sharp increase in fitting errors. This study theoretically proves the error propagation process of MLKG and shows that by introducing the sub-layer KG model and hierarchical structure will reduce the error. To evaluate MLKG’s accuracy, we test it on two typical high-dimensional non-linearity functions namely the Rosenbrock function and Michalewicz function. We compared MLKG with contemporary KG surrogate using by mean squared error (MSE) and
![]() ${R^2}$
. Finally, the approach applies the MLKG approach to the reliability analysis of vane stator variables (RAVSV).
${R^2}$
. Finally, the approach applies the MLKG approach to the reliability analysis of vane stator variables (RAVSV).
This article is organised as follow: Section 2 introduces original KG and summarises the reasons why original KG are not applicable to high-dimensional problems as large sample demand and internal parameter calculation. Section 3 introduces the basic process of MLKG and decomposes the error of MLKG into fitting error and the transfer error, which are caused by multi-layer structure. This paper proves the applicability of MLKG to high-dimensional, expensive (computationally) and black-box functions. Section 4 mainly verifies the accuracy of MLKG through high-dimensional nonlinear mathematical functions. In Section 5, we use the RAVSV as an example to verify the correctness of the proposed surrogate model.
2.0 Difficulties in high-dimensional problems for kg surrogate
Original KG is a popular surrogate model technique that uses a Gaussian process to model the unknown function of interest. However, original KG has limitations when it comes to high-dimensional problems, such as large sample demand and internal parameter calculation. This subsection will highlight the challenges of original KG in high-dimensional problems such as the reliability analysis of VSV and introduce some of the contemporary KG surrogate model technique.
2.1 The original Kriging surrogate (KG)
Kriging surrogate postulates a combination of a global model plus departures:
Where
![]() $\hat y\left( \boldsymbol{x} \right)$
is the unknown function of interest,
$\hat y\left( \boldsymbol{x} \right)$
is the unknown function of interest,
![]() $\boldsymbol{f}\left( \boldsymbol{x} \right) = {\left[ {{f_1}\left( \boldsymbol{x} \right),{f_2}\left( \boldsymbol{x} \right), \ldots, {f_N}\left( \boldsymbol{x} \right)} \right]^T}$
are known functions (usually polynomial).
$\boldsymbol{f}\left( \boldsymbol{x} \right) = {\left[ {{f_1}\left( \boldsymbol{x} \right),{f_2}\left( \boldsymbol{x} \right), \ldots, {f_N}\left( \boldsymbol{x} \right)} \right]^T}$
are known functions (usually polynomial).
![]() $\boldsymbol\beta = \left[ {{\beta _1},{\beta _2}, \ldots, {\beta _N}} \right]$
are the unknown parameters.
$\boldsymbol\beta = \left[ {{\beta _1},{\beta _2}, \ldots, {\beta _N}} \right]$
are the unknown parameters.
![]() $Z\left( \boldsymbol{x} \right)$
is assumed to be a realisation of a stochastic process. Several choices for these components are listed in Tables 1 and 2. Based on the selection of the regression component
$Z\left( \boldsymbol{x} \right)$
is assumed to be a realisation of a stochastic process. Several choices for these components are listed in Tables 1 and 2. Based on the selection of the regression component
![]() $\boldsymbol{f}{\left( \boldsymbol{x} \right)^T}$
, there are several variants of KG, such as simple KG and universal KG. Simple KG assumes the term
$\boldsymbol{f}{\left( \boldsymbol{x} \right)^T}$
, there are several variants of KG, such as simple KG and universal KG. Simple KG assumes the term
![]() $\boldsymbol{f}{\left( \boldsymbol{x} \right)^T}$
to be a constant, and universal KG assumes any other prespecified function
$\boldsymbol{f}{\left( \boldsymbol{x} \right)^T}$
to be a constant, and universal KG assumes any other prespecified function
![]() $\boldsymbol{x}$
. Universal KG,
$\boldsymbol{x}$
. Universal KG,
![]() $\boldsymbol{f}{\left( \boldsymbol{x} \right)^T}$
usually takes the form of a lower order polynomial regression. The one-order and second-order polynomials are used as the universal KG in this research and compared to simple KG.
$\boldsymbol{f}{\left( \boldsymbol{x} \right)^T}$
usually takes the form of a lower order polynomial regression. The one-order and second-order polynomials are used as the universal KG in this research and compared to simple KG.
Table 1. Regression models of KG

Table 2. Correlation models of KG

The random variables
![]() $\boldsymbol{Z}\left( \boldsymbol{x} \right)$
in KG are assumed to be correlated according to a correlation model. The covariance matrix is given as:
$\boldsymbol{Z}\left( \boldsymbol{x} \right)$
in KG are assumed to be correlated according to a correlation model. The covariance matrix is given as:
Here,
![]() $\boldsymbol\sigma $
is standard deviation of input samples and
$\boldsymbol\sigma $
is standard deviation of input samples and
![]() $R\left( {{\boldsymbol{x}^i},{\boldsymbol{x}^j}} \right)$
is the correlation function between sampled data points
$R\left( {{\boldsymbol{x}^i},{\boldsymbol{x}^j}} \right)$
is the correlation function between sampled data points
![]() ${\boldsymbol{x}^i}$
and
${\boldsymbol{x}^i}$
and
![]() ${\rm{\;}}{\boldsymbol{x}^j}$
. Correlation models consider that the correlation effect decreases as the distance between two distinct samples increases. KG is a local approximation method and require substantial computational time when the sample dataset is dominated by costly internal parameter optimisation [Reference Han, Song, Han and Wang17]. Additionally, the correlation matrix of KG becomes singular if multiple sample points are located closely. Furthermore, with a plethora of regression and correlation models available in the literature, choosing the appropriate KG model can be challenging. As a result, the original KG method is not suitable for high-dimensional input problems.
${\rm{\;}}{\boldsymbol{x}^j}$
. Correlation models consider that the correlation effect decreases as the distance between two distinct samples increases. KG is a local approximation method and require substantial computational time when the sample dataset is dominated by costly internal parameter optimisation [Reference Han, Song, Han and Wang17]. Additionally, the correlation matrix of KG becomes singular if multiple sample points are located closely. Furthermore, with a plethora of regression and correlation models available in the literature, choosing the appropriate KG model can be challenging. As a result, the original KG method is not suitable for high-dimensional input problems.
2.2 Some of the contemporary KG surrogate
The KG surrogate has become increasingly popular due to its flexibility in accurately imitating the dynamics of computationally expensive simulations and its ability to estimate the error of the predictor. Some recent works have addressed these drawbacks of original Kriging surrogate. Bouhlel [Reference Bouhlel and Bartoli23] present a new method that combines the Kriging surrogate with the partial least squares (KPLS) technique to obtain a fast predictor. The partial least squares technique reduces dimension and reveals how inputs depend on outputs. The combination of Kriging and partial least squares allows to build a fast-Kriging model because it requires fewer hyper-parameters in its covariance function. Zhao [Reference Zhao, Wang, Song, Wang and Dong29] proposes a method hat tcombines Kriging surrogate with maximal information coefficient (MIC), termed as KMIC. MIC is used to estimate the relative magnitude of the optimised hyper-parameters because both the optimised hyper-parameters and MIC can be used for global sensitivity analysis. To reduce the number of parameters that need to be optimised when estimating hyper-parameters, the maximum likelihood estimation problem is reformulated by adding a set of equality constraints. A high-dimensional Kriging method through principal component dimension reduction (HDKM-PCDR) is proposed in Ref. (Reference Li and Shi16). HDKM-PCDR can convert high-dimensional correlation parameters in the KG model into low-dimensional ones, which are used to reconstruct new correlation functions. The process of establishing correlation functions such as these can reduce the time consumption of correlation parameter optimisation and correlation function matrix construction in the modeling process.
In conclusion, this article compares MLKG with KMIC, KPLS and HDKM-PCDR by MSE and
![]() ${R^2}$
. Results show that MLKG can achieve an excellent level of accuracy in the reliability analysis of vane stator variables with a small number of sample points.
${R^2}$
. Results show that MLKG can achieve an excellent level of accuracy in the reliability analysis of vane stator variables with a small number of sample points.
3.0 A multi-layer kriging surrogate (mlkg) for high-dimensional and computationally expensive problems
In this section, the MLKG is proposed to improve the computing accuracy and efficiency for the reliability analysis of VSV. In practical industrial design applications, if all input variables are independent, each parameter can be designed individually. Therefore, the interest function can be easily decomposed into a combination of sub-models. This idea is also named ‘distributed collaboration’ or ‘decompose’. Bai [Reference Xiao, Zuo and Zhou9, Reference Huang and Du10] first proposed the concept of distributed collaboration and structured the mathematical model of distributed collaborative response surface method (DCRSM) for mechanical dynamic assembly reliability design. Through Bai’s work, the results show that the DCRSM cannot only overcome the complex issues that are difficult to address by the traditional methods but also significantly save computation time while preserving computational accuracy. However, Bai used the polynomial regression [Reference Zhou and Lu19] and support vector machine (SVM) [Reference Hu, Rui, Gao, Gou and Gong18] as sub-surrogate models to construct DCRSM. The polynomial regression has the drawbacks of poor nonlinearity, and SVM requires a large number of labeled samples as input dimension increases [Reference Deng20]. It is a challenge to use DCRSM in the reliability analysis of VSVs. Therefore, we propose a novel MLKG to address these issues.
3.1 Overview of MLKG
This paper solves the difficulties of the reliability analysis of VSVs through the idea of decomposition. The MLKG works by using the output of one KG model as the input to the next. In this way, the MLKG can capture the complex interactions between the inputs and outputs of the problem, while maintaining a high degree of accuracy and efficiency.
3.2 Mathematical model of MLKG
This sub-section establishes the mathematical model of MLKG. When
![]() $y\left( \boldsymbol{x} \right)$
and
$y\left( \boldsymbol{x} \right)$
and
![]() $\boldsymbol{x} = \left[ {{x_1},{x_2}, \ldots, {x_n}} \right]$
are output response and random variables, respectively. Assuming that the interest function involves
$\boldsymbol{x} = \left[ {{x_1},{x_2}, \ldots, {x_n}} \right]$
are output response and random variables, respectively. Assuming that the interest function involves
![]() $m$
objects and each object refers to
$m$
objects and each object refers to
![]() $n\left( {n \in {Z^ + }} \right)$
subjects, the interest function can be divided into multiple single-objects. If
$n\left( {n \in {Z^ + }} \right)$
subjects, the interest function can be divided into multiple single-objects. If
![]() ${\boldsymbol{x}^{\left( p \right)}}$
is the input parameter of the p-th object and
${\boldsymbol{x}^{\left( p \right)}}$
is the input parameter of the p-th object and
![]() ${y^{\left( p \right)}}$
is the output response, their relationship is denoted by:
${y^{\left( p \right)}}$
is the output response, their relationship is denoted by:
This relationship is called single-object Kriging surrogate (SKG). Similarly, the output responses
![]() $\left\{ {{y^{\left( p \right)}}} \right\}$
of all single objects are taken as the random input variables
$\left\{ {{y^{\left( p \right)}}} \right\}$
of all single objects are taken as the random input variables
![]() $\hat{\boldsymbol{x}}$
of the whole MLKG by:
$\hat{\boldsymbol{x}}$
of the whole MLKG by:
This relationship is called a collaborative Kriging surrogate (CKG). As shown by the above analysis, the complex function of the system is decomposed into multiple sub-systems. SKG and CKG consist of regression components and correlation components. This paper compares different regression and correlation model combinations to ensure that the MLKG has excellent accuracy.
3.3 The error propagation of MLKG
MLKG has good generality for the reliability analysis of VSVs. We assume the response of the problem is
![]() $f\left( {{\boldsymbol{x}_1}, \ldots, {x_i}, \ldots, {x_N}} \right)$
.
$f\left( {{\boldsymbol{x}_1}, \ldots, {x_i}, \ldots, {x_N}} \right)$
.
![]() ${\rm{\;}}{x_i}\left( {i \in 1,2, \ldots, N} \right)$
is the i-th design variable. According to the basic principle of MLKG, the response function
${\rm{\;}}{x_i}\left( {i \in 1,2, \ldots, N} \right)$
is the i-th design variable. According to the basic principle of MLKG, the response function
![]() $\boldsymbol{f}\left( {{x_1}, \ldots, {x_i}, \ldots, {x_N}} \right)$
is decomposed into m layers and each layer contains
$\boldsymbol{f}\left( {{x_1}, \ldots, {x_i}, \ldots, {x_N}} \right)$
is decomposed into m layers and each layer contains
![]() ${{\rm{n}}_{\rm{k}}}$
sub-models. The total error of MLKG is determined by the error of each sub model. To calculate the total error, we first prove the source of error for sub model in MLKG. The error of the j-th (
${{\rm{n}}_{\rm{k}}}$
sub-models. The total error of MLKG is determined by the error of each sub model. To calculate the total error, we first prove the source of error for sub model in MLKG. The error of the j-th (
![]() $j \in 1,2, \ldots, k$
) sub model in l-th (
$j \in 1,2, \ldots, k$
) sub model in l-th (
![]() $l \in 1,2, \ldots, m$
) layer satisfies the following formula:
$l \in 1,2, \ldots, m$
) layer satisfies the following formula:
Where
![]() $\hat y_{j,p}^l$
is surrogate modeling response of the p-th samples and
$\hat y_{j,p}^l$
is surrogate modeling response of the p-th samples and
![]() $y_{j,p}^l$
is the real response. The
$y_{j,p}^l$
is the real response. The
![]() $erro{r_{l,j}}$
is mainly composed of two parts. The first part is the error generated by the surrogate modeling, which is called fitting error. The other part is the error caused by incorrect input (usually cause by other sub-layer models), which is called transfer error. Therefore, we split the
$erro{r_{l,j}}$
is mainly composed of two parts. The first part is the error generated by the surrogate modeling, which is called fitting error. The other part is the error caused by incorrect input (usually cause by other sub-layer models), which is called transfer error. Therefore, we split the
![]() $erro{r_{l,j}}$
into fitting error and transfer error by the following formula:
$erro{r_{l,j}}$
into fitting error and transfer error by the following formula:
 \begin{align} erro{r_{i,j}} &= \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - y_{j,p}^l} \right|}^2}}\nonumber \\[5pt] {\rm{ }} &= \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - \dot y_{j,p}^l + \dot y_{j,p}^l - y_{j,p}^l} \right|}^2}} \nonumber\\[5pt] {\rm{ }} &\le \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - \dot y_{j,p}^l} \right|}^2}} + \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\dot y_{j,p}^l - y_{j,p}^l} \right|}^2}} \end{align}
\begin{align} erro{r_{i,j}} &= \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - y_{j,p}^l} \right|}^2}}\nonumber \\[5pt] {\rm{ }} &= \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - \dot y_{j,p}^l + \dot y_{j,p}^l - y_{j,p}^l} \right|}^2}} \nonumber\\[5pt] {\rm{ }} &\le \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - \dot y_{j,p}^l} \right|}^2}} + \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\dot y_{j,p}^l - y_{j,p}^l} \right|}^2}} \end{align}
![]() $\dot y_{j,p}^l{\rm{\;}}$
indicates the real response of the sub-model when the input is correct.
$\dot y_{j,p}^l{\rm{\;}}$
indicates the real response of the sub-model when the input is correct.
![]() ${\rm{\;}}{R^2}$
is often used to evaluate for fitting error (see Section 4.2.1).
${\rm{\;}}{R^2}$
is often used to evaluate for fitting error (see Section 4.2.1).
![]() ${\rm{\;}}Vary_{j,p}^l{\rm{\;}}$
is the variance of
${\rm{\;}}Vary_{j,p}^l{\rm{\;}}$
is the variance of
![]() $y_{j,p}^l$
.
$y_{j,p}^l$
.
 \begin{align}R_{i,j}^2 = 1 - \frac{{\frac{1}{2}\sum\nolimits_{p = 1}^{p = {n_s}} {{{\left| {\dot y_{j,p}^l - y_{j,p}^l} \right|}^2}} }}{{Var\left( {y_{j,p}^l} \right)}}\end{align}
\begin{align}R_{i,j}^2 = 1 - \frac{{\frac{1}{2}\sum\nolimits_{p = 1}^{p = {n_s}} {{{\left| {\dot y_{j,p}^l - y_{j,p}^l} \right|}^2}} }}{{Var\left( {y_{j,p}^l} \right)}}\end{align}
The accuracy of the surrogate model needs to meet the requirements, which can be given by the following formula:
Where
![]() ${c_{l,j}}$
(often
${c_{l,j}}$
(often
![]() $ \geqslant $
0.9) is a constant number. Therefore, it is not difficult to obtain from the two formulas.
$ \geqslant $
0.9) is a constant number. Therefore, it is not difficult to obtain from the two formulas.
Take the maximum fitting error of all samples as A, and A meet the following formula:
Therefore, by selecting the constant
![]() ${c_{l,j}}$
, it is not difficult to obtain
${c_{l,j}}$
, it is not difficult to obtain
 \begin{align}A \le \sqrt {\frac{{2*\left( {1 - {c_{i,j}}} \right)*Var\left( {y_{j,p}^l} \right)}}{{{n_s}}}} \end{align}
\begin{align}A \le \sqrt {\frac{{2*\left( {1 - {c_{i,j}}} \right)*Var\left( {y_{j,p}^l} \right)}}{{{n_s}}}} \end{align}
From the above derivation, it can be found that the fitting error is mainly controlled by
![]() ${\rm{\;}}Vary_{j,p}^l$
(
${\rm{\;}}Vary_{j,p}^l$
(
![]() ${c_{l,j}}$
and
${c_{l,j}}$
and
![]() ${n_s}$
are generally set constants). Therefore, reducing the variance of
${n_s}$
are generally set constants). Therefore, reducing the variance of
![]() $y_{j,p}^l$
can improve the fitting error. MLKG reduces the input dimension of each sub model compare with the whole model. Therefore, MLKG reduces
$y_{j,p}^l$
can improve the fitting error. MLKG reduces the input dimension of each sub model compare with the whole model. Therefore, MLKG reduces
![]() $Vary_{j,p}^l$
for fitting error.
$Vary_{j,p}^l$
for fitting error.
Unlike the fitting error, the transfer error is mainly affected by the multi-layer structure. The transfer error can be regarded as the combination of all response from the (l-1) th layer. The transfer error is
 \begin{align} \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - \dot y_{j,p}^l} \right|}^2}} &= \sum\limits_{p = 1}^{p = {n_s}} {\sum\limits_{o = 1}^{o = {n_l} - 1} {\frac{{\partial \hat y_{j,p}^l}}{{\partial \dot y_o^{l - 1}}}\left( {\hat y_o^l - \dot y_o^{l - 1}} \right)} }\nonumber \\[5pt] {\rm{ }} &\le \sum\limits_{p = 1}^{p = {n_s}} {\sum\limits_{o = 1}^{o = {n_l} - 1} {\left| {\frac{{\partial \hat y_{j,p}^l}}{{\partial \dot y_o^{l - 1}}}} \right|\left| {\left( {\hat y_o^l - \dot y_o^{l - 1}} \right)} \right|} } \end{align}
\begin{align} \sum\limits_{p = 1}^{p = {n_s}} {{{\left| {\hat y_{j,p}^l - \dot y_{j,p}^l} \right|}^2}} &= \sum\limits_{p = 1}^{p = {n_s}} {\sum\limits_{o = 1}^{o = {n_l} - 1} {\frac{{\partial \hat y_{j,p}^l}}{{\partial \dot y_o^{l - 1}}}\left( {\hat y_o^l - \dot y_o^{l - 1}} \right)} }\nonumber \\[5pt] {\rm{ }} &\le \sum\limits_{p = 1}^{p = {n_s}} {\sum\limits_{o = 1}^{o = {n_l} - 1} {\left| {\frac{{\partial \hat y_{j,p}^l}}{{\partial \dot y_o^{l - 1}}}} \right|\left| {\left( {\hat y_o^l - \dot y_o^{l - 1}} \right)} \right|} } \end{align}
In (13),
![]() $\left| {\frac{{\partial \hat y_{j,p}^l}}{{\partial y_o^{l - 1}}}} \right|$
is the derivative of the j-th surrogate model in l-th layer with the input of (l-1)-th layer,
$\left| {\frac{{\partial \hat y_{j,p}^l}}{{\partial y_o^{l - 1}}}} \right|$
is the derivative of the j-th surrogate model in l-th layer with the input of (l-1)-th layer,
![]() $\left| {\hat y_o^{l - 1} - \dot y_o^{l - 1}} \right|$
is the transfer error from (l-1) layer. It is not difficult to find that as long as
$\left| {\hat y_o^{l - 1} - \dot y_o^{l - 1}} \right|$
is the transfer error from (l-1) layer. It is not difficult to find that as long as
![]() $\left| {\frac{{\partial \hat y_{j,p}^l}}{{\partial y_o^{l - 1}}}} \right| \le 1$
, the transfer error become smaller by multiple layer structures. So the transfer error does not increase with MLKG. Therefore, through the above proof, it is verified that MLKG decomposes the structure and establishes different sub surrogate models is theoretically universal.
$\left| {\frac{{\partial \hat y_{j,p}^l}}{{\partial y_o^{l - 1}}}} \right| \le 1$
, the transfer error become smaller by multiple layer structures. So the transfer error does not increase with MLKG. Therefore, through the above proof, it is verified that MLKG decomposes the structure and establishes different sub surrogate models is theoretically universal.
4.0 Performance of numerical test
We compared MLKG with the some of the contemporary KG surrogate modeling technique by mean squared error and
![]() ${R^2}$
. Two explicit mathematical functions are selected as the test cases for testing the highly nonlinear optimisation algorithms. Results show that MLKG can achieve an excellent level of accuracy for reliability analysis in high-dimensional problems with a small number of sample points.
${R^2}$
. Two explicit mathematical functions are selected as the test cases for testing the highly nonlinear optimisation algorithms. Results show that MLKG can achieve an excellent level of accuracy for reliability analysis in high-dimensional problems with a small number of sample points.
4.1 Test function
(a) A 100-D Rosenbrock function with low non-order linearity
The Rosenbrock function, the Valley or Banana function, is a famous test problem for gradient-based optimisation algorithms. The function is unimodal, and the global minimum lies in a narrow, parabolic valley (Fig. 3). However, even though this valley is easy to find, convergence to the minimum is difficult. The recommended value of d is 100 in this article.

Figure 3. Rosenbrock function’s two-dimensional form.
In the Rosenbrock function example, the function is decomposed into 99 parts listed in Equation (15). Next, 99 single-object SKGsare constructed to replace equation. Using the output of the SKGs from equation as inputs and the output of equation as the result, a collaborative SKG of Rosenbrock function is constructed.
Then, sample
![]() ${y_i}\left( x \right)$
and construct CKG as follows:
${y_i}\left( x \right)$
and construct CKG as follows:
(b) A 100-D Michalewicz function with high-order nonlinearity
The Michalewicz function has d! local minima, and it is multimodal. The function’s two-dimensional form is shown in Fig. 4. The parameter m defines the steepness of the valleys and ridges; a larger m leads to a more difficult search. This article’s recommended values of d and m are 100 and 10. The Michalewicz function is decomposed into 100 parts, which are as follows:

Figure 4. Michalewicz function’s two-dimensional form.
Then, 100 single-object SKGs are constructed to replace equation (17). Using the output of the SKGs from equation (17) as inputs and the output of equation (18) as the result, a collaborative SKG of the Michalewicz function is constructed.
4.2 The evaluation method of test function
For accuracy, the goodness of fit obtained from sample points is insufficient to assess newly predicted points’ accuracy. Thus, additional error analysis points are employed to verify the accuracy of all the surrogate models; this paper uses two metrics: R square (R 2) and MSE.
(a) R square
R square is a widely used assessment metric for surrogate models, which is used in the study to make a quantitative assessment of the fitting performance of a surrogate model. The definitions of
![]() ${R^2}$
are listed:
${R^2}$
are listed:
 \begin{align}{R^2} = 1 - \frac{{\sum\limits_{i = 1}^m {{{\left( {y\left( {{x_i}} \right) - \hat y\left( {{x_i}} \right)} \right)}^2}} }}{{\sum\limits_{i = 1}^m {{{\left( {y\left( {{x_i}} \right) - \bar y\left( {{x_i}} \right)} \right)}^2}} }}\end{align}
\begin{align}{R^2} = 1 - \frac{{\sum\limits_{i = 1}^m {{{\left( {y\left( {{x_i}} \right) - \hat y\left( {{x_i}} \right)} \right)}^2}} }}{{\sum\limits_{i = 1}^m {{{\left( {y\left( {{x_i}} \right) - \bar y\left( {{x_i}} \right)} \right)}^2}} }}\end{align}
Where m is the total number of error analysis points,
![]() $\hat y\left( {{x_i}} \right)$
is the corresponding predicted value for the observed value
$\hat y\left( {{x_i}} \right)$
is the corresponding predicted value for the observed value
![]() $y\left( {{x_i}} \right)$
,
$y\left( {{x_i}} \right)$
,
![]() $\bar y\left( {{x_i}} \right)$
is the mean of the experimental values. The larger the value of
$\bar y\left( {{x_i}} \right)$
is the mean of the experimental values. The larger the value of
![]() ${R^2}$
, the more accurate the surrogate model.
${R^2}$
, the more accurate the surrogate model.
(b) Mean squared error (MSE)
Where
![]() $\hat y\left( {{x_i}} \right)$
is the prediction value obtained by the surrogate model, and
$\hat y\left( {{x_i}} \right)$
is the prediction value obtained by the surrogate model, and
![]() $y\left( {{x_i}} \right)$
is the real response values. The smaller the MSE is, the higher the fitting accuracy of the surrogate model will be.
$y\left( {{x_i}} \right)$
is the real response values. The smaller the MSE is, the higher the fitting accuracy of the surrogate model will be.
4.3 Design of experiments (DOEs)
When constructing a surrogate model, it is important to select the sample points for the accuracy of the surrogate model. Generally, it is required that the selected sample points can evenly cover the entire design space, and the number of sample points should be as few as possible. Considering these two requirements, this article uses the Latin hypercube sampling (LHS) for sampling. The minimum number of sample points for the original KG surrogate should be more than
![]() $2d + 1$
. Because the test function dimension in this paper is 100, the number of sample points needs to be more than 201, so the number of sample points starts from 250. We compare the accuracy of the original KG and some new KG surrogate by
$2d + 1$
. Because the test function dimension in this paper is 100, the number of sample points needs to be more than 201, so the number of sample points starts from 250. We compare the accuracy of the original KG and some new KG surrogate by
![]() ${R^2}$
and MSE. The sample points are listed in Table 3.
${R^2}$
and MSE. The sample points are listed in Table 3.
Table 3. DOEs

4.4 Numerical test result
(a) Rosenbrock function
It is not difficult to see from the R square (Fig. 5) that both the original KG and MLKG can realise the fitting of the Rosenbrock function. Still, when the number of sample points is small (sample points less than 300), the original KG performance is very poor (
![]() ${R^2} \lt 0.1$
). With the increase of points, its accuracy improves, but even when the number of sample points reaches 600, the accuracy of the original KG is only 0.6. Different from the original KG, MLKG still maintains high accuracy (
${R^2} \lt 0.1$
). With the increase of points, its accuracy improves, but even when the number of sample points reaches 600, the accuracy of the original KG is only 0.6. Different from the original KG, MLKG still maintains high accuracy (
![]() ${R^2} \gt 0.99$
) even when the number of samples is minimal.
${R^2} \gt 0.99$
) even when the number of samples is minimal.

Figure 5.
![]() ${{\bf{R}}^2}$
for Rosenbrock function.
${{\bf{R}}^2}$
for Rosenbrock function.
In order to further verify the accuracy of MLKG, this article compared several new high-dimensional KG models. In view of the above shortcomings of the traditional KG, many scholars used several methods to improve the traditional Kriging model, such as Partial Least Squares dimension reduction (KMIC,KPL) [Reference Zhu8, Reference Cheng, Lu, Zhou, Shi and Wei26]. The results are shown in Fig. 6. Compared to these latest high-dimensional KG models, MLKG accuracy (
![]() ${R^2} \gt 0.99$
) is highest than others KG models (
${R^2} \gt 0.99$
) is highest than others KG models (
![]() ${R^2} \le 0.8$
). It is because MLKG reduces the decoupling between the final output and random variables by adding a sub surrogate model layer.
${R^2} \le 0.8$
). It is because MLKG reduces the decoupling between the final output and random variables by adding a sub surrogate model layer.

Figure 6. Compared with several new high-dimensional KG models.
(b) Michalewicz function
Compared with the Rosenbrock function, the original KG surrogate and MLKG are much harder to fit the Michalewicz function. As mentioned before, the larger the R square, the more accurate the surrogate model is; however, for MSE, a smaller value indicates better accuracy. From Fig. 7, it is evident that when the number of sample points is increasing, the accuracy of the original KG is relatively poor (R 2 < 0.1), while the MLKG surrogate model obtains a good level of accuracy. It can be found from Fig. 7 that the accuracy of the original KG surrogate on the high-dimensional nonlinear function is not feasible, which is similar to the conclusion of the article [Reference Zhu8].

Figure 7.
![]() ${{\bf{R}}^2}$
for Michalewicz function.
${{\bf{R}}^2}$
for Michalewicz function.
It can be found that with the increase of sample points, the MSE of MLKG gradually decreases (Fig. 8). However, the original KG surrogate has no obvious downward trend, which means that for typical high-dimensional nonlinear functions such as the Michalewicz function, it is difficult to improve the accuracy by increasing the number of samples. The high-dimensional Michalewicz and Rosenbrock function shows that MLKG is suitable for fitting high-dimensional and high-nonlinearity functions. The accuracy remains stable when there are few sample points.

Figure 8. MSE for Michalewicz function.
In order to further verify the accuracy of MLKG, this article compared several new high-dimensional KG models (HDKM-PCDR, KPLS). The results are shown in Fig. 9.

Figure 9. Compared with several new high-dimensional KG models by MSE.
In summary, MLKG is a novel approach for solving RAVSV problems, by decomposing the interest function into multiple sub-models and using collaborative Kriging surrogate models to analyse the responses of each sub-model. Compared to traditional KG and other new high-dimensional KG models, MLKG shows superior accuracy and generality.
5.0 Application
In this section, we will utilise the RAVSV in an aero-engine as an example to demonstrate the accuracy of the proposed surrogate model. The VSVs (Fig. 1) are responsible for blade angle adjustments and are an indispensable component that significantly affects the aero-engine’s efficiency and reliability. The VSV contains more than 30 objects (Fig. 2) and 64 random variables (Table 4).
5.1 The RAVSVs
The RAVSV process includes the five steps shownin Fig. 10. Firstly, the VSV is decomposed into several individual parts as shown in Fig. 2. FE simulation is then performed to obtain displacement and deflection angle of all the single parts. Thirdly, we investigate the sensitivity of the blade deflection angle and select important parts with variables sensitivity greater than 2%. For these selected parts, we establish a single object Kriging surrogate model. The single-object KG is then sampled to construct the collaborative Kriging surrogate model of blade angle. Finally, the MCS will be performed based on the MLKG to obtain reliability analysis results of VSV.
5.2 Random variable selection
VSV is a highly complex system comprising more than 30 components, such as blades, actuators, outer rings, inner rings and so on. The sources of uncertainties mainly arise from geometric, frictional and material factors. For completeness, the RAVSV process considers geometric, young’s modulus and friction coefficient uncertainties, as shown in Table 4. These parameters are assumed to be mutually independent and object to a uniform distribution. Based on the primary thought of MLKG, VSV is divided into several deflection degree analyses of double rocker (Fig. 11), outer ring (Fig. 12), actuator (Fig. 13), pins, rods and other structures.
Table 4. The total 64 random variables in 34 objects

5.3 Finite element simulation
The VSV system is designed with a bush on the casing and inner ring, as well as contact constraints between the bush and the blade shaft. The actuator piston moves 50mm along the axial direction, while a pneumatic torque of
![]() $840{\rm{N}\,\bullet\,\rm{mm}}$
is applied to the blade shaft in the same direction as the blade rotation. The rocker arm and linkage ring are considered flexible parts in the simulation. All parts are made of Ti-6AL-4V(TC4) material. All FE simulations are automated in the RAVSV process, and the output is the deflection degree of the blade. As shown in Fig. 14, the time of movement is
$840{\rm{N}\,\bullet\,\rm{mm}}$
is applied to the blade shaft in the same direction as the blade rotation. The rocker arm and linkage ring are considered flexible parts in the simulation. All parts are made of Ti-6AL-4V(TC4) material. All FE simulations are automated in the RAVSV process, and the output is the deflection degree of the blade. As shown in Fig. 14, the time of movement is
![]() $0.0008s$
, the rotation angle of the blade is about
$0.0008s$
, the rotation angle of the blade is about
![]() $34.75^\circ $
and the movement of the blade is complex and non-linear. The whole FE simulation process takes 2h. Thus, relying on the finite element method to evaluate the reliability of VSV is very time-consuming.
$34.75^\circ $
and the movement of the blade is complex and non-linear. The whole FE simulation process takes 2h. Thus, relying on the finite element method to evaluate the reliability of VSV is very time-consuming.

Figure 10. The reliability analysis of the vane stator variables.

Figure 11. Geometric parameter of double rocker.

Figure 12. Geometric parameter of the outer ring.

Figure 13. Geometric parameter of the actuator.

Figure 14. FE simulation of blade degree.
According to the Morris global sensitivity analysis method [Reference Morris30], we analysed the output sensitivity of the blade deflection angle with each random variables (Table 5). The purpose of using sensitivity analysis here is not to select the random variables that have the greatest impact on the results, but to identify the parts that have the greatest impact on the final results. For these important parts, we established a single-object Kriging surrogate model. The other factors affecting the blade adjustment accuracy have a minor impact, with sensitivity analysis results below 1% and are not listed in the table. Among the various components, the elastic modulus of the TC4 material has the most significant impact on blade adjustment accuracy, followed by the variables of rocker arms, linkage rings and double rocker arms. From the results, it is evident that the linkage ring, pin and rocker have the most significant impact on the blade deflection angle, along with the material parameters. Hence, we establish a single-object surrogate model for these three parts.
Table 5. Sensitivity of VSV based on Morris method

5.4 Single-object Kriging surrogate model
The deflection angle of blades in VSV is mainly affected by the randomness of the linkage ring, pin and rocker. The reliability of VSV is gained by the limit state function as:
Where
![]() $f\left( {{Y_b}\left( {{x_b}} \right),{Y_c}\left( {{x_c}} \right),{Y_d}\left( {{x_d}} \right)} \right)$
are the regression models of SKG, and rocker and
$f\left( {{Y_b}\left( {{x_b}} \right),{Y_c}\left( {{x_c}} \right),{Y_d}\left( {{x_d}} \right)} \right)$
are the regression models of SKG, and rocker and
![]() $Z\left( {{Y_b}\left( {{x_b}} \right),{Y_c}\left( {{x_c}} \right),{Y_d}\left( {{x_d}} \right)} \right)$
correlation models of SKG.
$Z\left( {{Y_b}\left( {{x_b}} \right),{Y_c}\left( {{x_c}} \right),{Y_d}\left( {{x_d}} \right)} \right)$
correlation models of SKG.
![]() $\delta $
represents a random variable associated with the linkage ring, pin, and rocker, which defines the desired deflection angle. As we all know, Y<0 denotes the failure of the VSV. As the idea of decomposition, we established the SKG as:
$\delta $
represents a random variable associated with the linkage ring, pin, and rocker, which defines the desired deflection angle. As we all know, Y<0 denotes the failure of the VSV. As the idea of decomposition, we established the SKG as:
 \begin{align} {Y_b}\left( {{x_b}} \right) &= f{\left( {{x_b}} \right)^T}\boldsymbol\beta + \boldsymbol{Z}\left( {{x_b}} \right)\nonumber \\[5pt] {Y_c}\left( {{x_c}} \right) &= f{\left( {{x_c}} \right)^T}\boldsymbol\beta + \boldsymbol{Z}\left( {{x_c}} \right)\nonumber \\[5pt] {Y_d}\left( {{x_d}} \right) &= f{\left( {{x_d}} \right)^T}\boldsymbol\beta + \boldsymbol{Z}\left( {{x_d}} \right) \end{align}
\begin{align} {Y_b}\left( {{x_b}} \right) &= f{\left( {{x_b}} \right)^T}\boldsymbol\beta + \boldsymbol{Z}\left( {{x_b}} \right)\nonumber \\[5pt] {Y_c}\left( {{x_c}} \right) &= f{\left( {{x_c}} \right)^T}\boldsymbol\beta + \boldsymbol{Z}\left( {{x_c}} \right)\nonumber \\[5pt] {Y_d}\left( {{x_d}} \right) &= f{\left( {{x_d}} \right)^T}\boldsymbol\beta + \boldsymbol{Z}\left( {{x_d}} \right) \end{align}
Figure 15 shows the comparison between MLKG and original KG model by MSE with same regression models and correlation models for RAVSV. It is not difficult to find out from the results that MLKG is more accurate than the original KG, and the original KG cannot predict the reliability problem with high-dimensional input. For further discussion, Fig. 16 shows the MSE and
![]() ${R^2}$
with different regression models and correlation models for MLKG in RAVSV. Zero-exp represents the combination of constant regression and exp correlation. One-exp represents the combination of one-order regression and exp correlation. It is not difficult to see from the results that the accuracy is the highest when the regression function is of a one-order function, and the correlation function is an exp function.
${R^2}$
with different regression models and correlation models for MLKG in RAVSV. Zero-exp represents the combination of constant regression and exp correlation. One-exp represents the combination of one-order regression and exp correlation. It is not difficult to see from the results that the accuracy is the highest when the regression function is of a one-order function, and the correlation function is an exp function.

Figure 15. MSE comparison between the original KG and MLKG.

Figure 16. Different MLKGs in RAVSV.
After choosing the regression model and correlation models, the SKG is established. According to the Equations (21), we established the SKG for the linkage ring, pin and rocker. Then SKG were simulated
![]() ${10^5}$
times. The results of SKG are listed in Figs. 17, 18 and 19. From results, it can be observed that the angles of the linkage ring, pin and double rocker are all normally distributed (Table 6). The mean and variance of the linkage ring are 4.47 and 0.02. The mean and variance of the pin are 34.75 and 0.50. The mean and variance of the double rocker angle are 42.30 and 0.23.
${10^5}$
times. The results of SKG are listed in Figs. 17, 18 and 19. From results, it can be observed that the angles of the linkage ring, pin and double rocker are all normally distributed (Table 6). The mean and variance of the linkage ring are 4.47 and 0.02. The mean and variance of the pin are 34.75 and 0.50. The mean and variance of the double rocker angle are 42.30 and 0.23.

Figure 17. Pin rotation degree distribution.

Figure 18. Ring rotation degree distribution.

Figure 19. Double rocker rotation degree distribution.
5.5 The deflection degree distribution of blades
Based on the sensitivity analysis results, it has been determined that the pin, linkage ring and double rockers are the primary components that affect the blade rotation. Finite element simulations were conducted to obtain the rotation angles of these parts under various random variables, and single-object SKGs were established for each component. The SKGs were then sampled to build a collaborative Kriging surrogate model for blade deflection angle (Fig. 20). The surrogate model for blade deflection angle was extracted
![]() ${10^5}$
times, and the results are depicted in Fig. 20.
${10^5}$
times, and the results are depicted in Fig. 20.
The results show that the mean value is
![]() ${\rm{\;}}34.57^\circ $
, the distribution is normal distribution, the variance is
${\rm{\;}}34.57^\circ $
, the distribution is normal distribution, the variance is
![]() $0.18^\circ 0.18$
° and the maximum value of deflection angle is
$0.18^\circ 0.18$
° and the maximum value of deflection angle is
![]() $37.05^\circ $
. The minimum value of deflection angle is
$37.05^\circ $
. The minimum value of deflection angle is
![]() $32.25^\circ $
. According to the requirements of high reliability of aero-engine, the desired deflection degree of blade requires more than
$32.25^\circ $
. According to the requirements of high reliability of aero-engine, the desired deflection degree of blade requires more than
![]() $34.03^\circ $
when the reliability of VSV reaches 99.74%.
$34.03^\circ $
when the reliability of VSV reaches 99.74%.
Table 6. Sample the SKG for building the surrogate model of blade deflection angle


Figure 20. Result for RAVSV.
6.0 Conclusion
This article aims at solving the difficulties from the reliability analysis of VSVs. We propose a novel multi-layer MLKG. The MLKG is a combination of multiple Kriging surrogate models that are arranged in a hierarchical structure, where each layer represents a different level of abstraction. By breaking the reliability analysis of VSVs down into smaller problems, MLKG decomposes the large surrogate model and reduces the input dimension of sub-layer KG model. In this way, the MLKG can capture the complex interactions between the inputs and outputs of the problem, while maintaining a high degree of accuracy and efficiency. Some in conclusion are listed as follow:
-
(1) This paper focuses on the reliability analysis of VSVs and proposes a novel surrogate model based on KG and decomposition. Our approach is to decompose the VSVs into several low-dimensional sub-models and establish some single-object SKG models. After establishing SKGs, we construct the general collaborative KG surrogate for reliability analysis.
-
(2) To verify the accuracy of the proposed method, this paper tests two typical high-dimensional non-linearity functions (Michalewicz function and Rosenbrock function). It is evident that when the number of sample points is increasing, the accuracy of the original KG is relatively poor (R 2 < 0.6), while the MLKG surrogate model obtains a good level of accuracy (R 2 > 0.9).
-
(3) This study theoretically proves the error propagation process of the proposed method and shows that by introducing the sub-layer Kriging model and hierarchical structure will reduce the error. We compared MLKG with contemporary Kriging surrogate using by mean squared error (MSE) and
 ${R^2}$
.
${R^2}$
. -
(4) The approach is represented by the RAVSV. The results show that the mean value of blade deflection angle of VSV is
 $34.57^\circ $
, the distribution is normal distribution, the variance is
$34.57^\circ $
, the distribution is normal distribution, the variance is
 $0.18^\circ 0.18$
°, the maximum value of deflection angle is
$0.18^\circ 0.18$
°, the maximum value of deflection angle is
 $37.05^\circ $
. The minimum value of deflection angle is
$37.05^\circ $
. The minimum value of deflection angle is
 $32.25^\circ $
. According to the requirements of high reliability of aero-engine, the desired deflection degree of blade requires more than
$32.25^\circ $
. According to the requirements of high reliability of aero-engine, the desired deflection degree of blade requires more than
 $34.03^\circ $
when the reliability of VSV reaches 99.74%.
$34.03^\circ $
when the reliability of VSV reaches 99.74%.
Funding
This study was supported by the National Science and Technology Major Project of China (J2019-I-0008-0008 and J2019-IV-0002-0069).