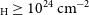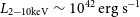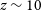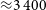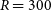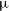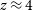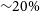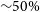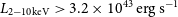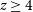Preface
The articles of this special issue focus on some of the major scientific questions that a future IR observatory will be able to address. We adopt the SPace Infrared telescope for Cosmology and Astrophysics (SPICA) design as a baseline to demonstrate how to achieve the major scientific goals in the fields of galaxy evolution, galactic star formation, and protoplanetary disks formation and evolution. The studies developed for the SPICA mission serve as a reference for future work in the field, even though the mission proposal has been cancelled by European Space Agency (ESA) from its M5 competition.
The mission concept of SPICA employs a 2.5-m telescope, actively cooled to below
![]() $\sim$
8 K, and a suite of mid- to far-IR spectrometers and photometric cameras, equipped with state-of-the-art detectors (Roelfsema et al. Reference Roelfsema2018). In particular, the SPICA Far-infrared Instrument (SAFARI) is a grating spectrograph with low (
$\sim$
8 K, and a suite of mid- to far-IR spectrometers and photometric cameras, equipped with state-of-the-art detectors (Roelfsema et al. Reference Roelfsema2018). In particular, the SPICA Far-infrared Instrument (SAFARI) is a grating spectrograph with low (
![]() $R\,\sim200$
–300) and medium (
$R\,\sim200$
–300) and medium (
![]() $R\,\sim3\,000$
–
$R\,\sim3\,000$
–
![]() $11\,000$
) resolution observing modes instantaneously covering the 35–
$11\,000$
) resolution observing modes instantaneously covering the 35–
![]() $210\,\unicode[Times]{x03BC}$
m wavelength range. The SPICA Mid-infrared Instrument (SMI) has three operating modes: a large field of view (
$210\,\unicode[Times]{x03BC}$
m wavelength range. The SPICA Mid-infrared Instrument (SMI) has three operating modes: a large field of view (
![]() $10' \times 12'$
) low-resolution 17–
$10' \times 12'$
) low-resolution 17–
![]() $36\,\unicode[Times]{x03BC}$
m imaging spectroscopic (
$36\,\unicode[Times]{x03BC}$
m imaging spectroscopic (
![]() $R\,\sim50$
–120) mode and photometric camera at
$R\,\sim50$
–120) mode and photometric camera at
![]() $34\, \unicode[Times]{x03BC}$
m (SMI-LR), a medium-resolution (
$34\, \unicode[Times]{x03BC}$
m (SMI-LR), a medium-resolution (
![]() $R\,\sim1\,300$
–
$R\,\sim1\,300$
–
![]() $2\,300$
) grating spectrometer covering wavelengths of 18–36
$2\,300$
) grating spectrometer covering wavelengths of 18–36
![]() $\unicode[Times]{x03BC}$
m (SMI-MR), and a high-resolution echelle module (
$\unicode[Times]{x03BC}$
m (SMI-MR), and a high-resolution echelle module (
![]() $R\sim29\,000$
) for the 10–18
$R\sim29\,000$
) for the 10–18
![]() $\unicode[Times]{x03BC}$
m domain (SMI-HR). Finally, magnetic field (B) explorer with BOlometric Polarimeter (B-BOP), a large field of view (
$\unicode[Times]{x03BC}$
m domain (SMI-HR). Finally, magnetic field (B) explorer with BOlometric Polarimeter (B-BOP), a large field of view (
![]() $2'.6 \times 2'.6$
), three-channel, (70, 200, and
$2'.6 \times 2'.6$
), three-channel, (70, 200, and
![]() $350\,\unicode[Times]{x03BC}$
m) polarimetric camera complements the science payload.
$350\,\unicode[Times]{x03BC}$
m) polarimetric camera complements the science payload.
1. Introduction
One of the main open issues in astrophysics is the role of supermassive black holes (SMBHs) in shaping the galaxies and the influence that the star formation (SF) has on the properties of the active galactic nuclei (AGN). The scaling relations between the mass of the SMBH and the stellar mass (or luminosity) of the spheroid in which it is hosted (Kormendy & Richstone Reference Kormendy and Richstone1995) or the spheroid velocity dispersion (Ferrarese & Merritt Reference Ferrarese and Merritt2000; Gebhardt et al. Reference Gebhardt2000) suggest a tight link between SF activity in the spheroidal components of galaxies and SMBH growth. The BH–galaxy co-evolution paradigm states that an intense phase of SF is triggered by a wet merger, at least for the most luminous and massive systems (Silk & Rees Reference Silk and Rees1998; Di Matteo, Springel, & Hernquist Reference Di Matteo, Springel and Hernquist2005; Lamastra et al. Reference Lamastra2013). A fraction of the gas reservoir of the galaxy is funneled towards the SMBH and turns on the AGN activity. Hydrodynamical simulations (e.g. Di Matteo et al. Reference Di Matteo, Springel and Hernquist2005; Hopkins et al. Reference Hopkins2006; Barai et al. Reference Barai2018), semianalytic models (e.g. Menci et al. Reference Menci, Fiore, Puccetti and Cavaliere2008), and observations (e.g. Tombesi et al. Reference Tombesi2015; Feruglio et al. Reference Feruglio2015; Smith et al. Reference Smith, Tombesi, Veilleux, Lohfink and Luminari2019) suggest a scenario where AGN provide feedback that regulates the SF in the host galaxies, thus originating the observed correlations. Such link between SMBH growth and galactic SF history is supported by the striking similarity of the evolution of the SMBH accretion rate (Black Hole Accretion Rate [BHAR]) and that of the star formation rate (SFR) densities, especially at high redshifts where the SF mostly occurs in the spheroidal components (Shankar, Weinberg, & Miralda-Escudé Reference Shankar, Weinberg and Miralda-Escudé2009; Fiore et al. Reference Fiore2017; Gruppioni et al. Reference Gruppioni2020). The evolutions of the SFR and the BHAR follow a parallel evolution, showing both a peak of activity around
![]() $z \approx 1{-}3$
, known as the ‘cosmic noon’ (Madau & Dickinson Reference Madau and Dickinson2014; Heckman & Best Reference Heckman and Best2014; Vito et al. Reference Vito2018). However, the mechanisms responsible for this similarity are not well understood and the co-evolution between galaxy and SMBH is still a matter of debate. Investigating the black hole (BH)–galaxy co-evolution requires sizable samples of galaxies and AGN over a broad range of redshift and luminosities to characterise the accretion and SF histories and disentangle the two contributions within the same source as accurately as possible.
$z \approx 1{-}3$
, known as the ‘cosmic noon’ (Madau & Dickinson Reference Madau and Dickinson2014; Heckman & Best Reference Heckman and Best2014; Vito et al. Reference Vito2018). However, the mechanisms responsible for this similarity are not well understood and the co-evolution between galaxy and SMBH is still a matter of debate. Investigating the black hole (BH)–galaxy co-evolution requires sizable samples of galaxies and AGN over a broad range of redshift and luminosities to characterise the accretion and SF histories and disentangle the two contributions within the same source as accurately as possible.
To study the link between SF and BH accretion we need, in particular, to investigate the epoch in which the bulk of these growths seems to take place (i.e. the cosmic noon). However, the high quantity of gas and dust that fuels both processes absorbs most of the energy emitted by stars and accreting SMBHs and re-emits it at longer wavelengths, mostly in the IR. The search for and the characterisation of these objects in the optical and UV are challenging due to the heavy reddening that affects them (Rowan-Robinson et al. Reference Rowan-Robinson1997; Hughes et al. Reference Hughes1998). A solution to this problem is to study indirectly the primary emission, by measuring the dust-reprocessed radiation in the IR. A study at such wavelengths allows us to observe the physical processes at work in the obscured regions and, therefore, to derive the SFR density (SFRD) and the BHAR density (BHAD) if we are capable of properly separating them. A direct measure of the dust-obscured SF activity is possible with space-based IR observatories, which do not need to be corrected by dust attenuation.
The mid- to far-IR photometric observations in deep fields (Delvecchio et al. Reference Delvecchio2014; Schreiber et al. Reference Schreiber2015) have provided extremely reliable determination of the SFRD and the BHAD up to redshift
![]() $\sim\!3{-}4$
(Gruppioni et al. Reference Gruppioni2013; Magnelli et al. Reference Magnelli2013; Delvecchio et al. Reference Delvecchio2014) using Herschel PACS data (observing at 100 and
$\sim\!3{-}4$
(Gruppioni et al. Reference Gruppioni2013; Magnelli et al. Reference Magnelli2013; Delvecchio et al. Reference Delvecchio2014) using Herschel PACS data (observing at 100 and
![]() $160\,\unicode[Times]{x03BC}$
m; Poglitsch et al. Reference Poglitsch2010) and have detected high redshift galaxies (up to
$160\,\unicode[Times]{x03BC}$
m; Poglitsch et al. Reference Poglitsch2010) and have detected high redshift galaxies (up to
![]() $z > 6$
; e.g. Riechers et al. Reference Riechers2013; Rowan-Robinson et al. Reference Rowan-Robinson2016) using SPIRE, observing at 250, 350, and
$z > 6$
; e.g. Riechers et al. Reference Riechers2013; Rowan-Robinson et al. Reference Rowan-Robinson2016) using SPIRE, observing at 250, 350, and
![]() $500\,\unicode[Times]{x03BC}$
m; Griffin et al. Reference Griffin2010). However, the deepest cosmological surveys performed by Herschel at high-z have detected only the most luminous galaxies (
$500\,\unicode[Times]{x03BC}$
m; Griffin et al. Reference Griffin2010). However, the deepest cosmological surveys performed by Herschel at high-z have detected only the most luminous galaxies (
![]() $L_{\rm IR} >10^{12}\,{\rm L}_{\odot}$
at
$L_{\rm IR} >10^{12}\,{\rm L}_{\odot}$
at
![]() $z\ge 3$
; Gruppioni et al. Reference Gruppioni2013) and suffer from the uncertainties of not being able to accurately disentangle the AGN from the SF emissions, as both contributes to the mid- and far-IR emission. Even in the case when spectral energy distribution (SED) fitting allows us to separate the two components, the results usually depend on the adopted technique and modelling. Therefore, the initial phase of the BH–galaxy co-evolution paradigm has been, so far, the most elusive and difficult to track. According to the co-evolution scenario, this heavily obscured phase should be characterised by the presence of a strong starburst and an obscured AGN, both giving a significant contribution to the mid- and far-IR emission (e.g. Page et al. Reference Page, Stevens, Ivison and Carrera2004; Vignali et al. Reference Vignali2009; Lapi et al. Reference Lapi2018).
$z\ge 3$
; Gruppioni et al. Reference Gruppioni2013) and suffer from the uncertainties of not being able to accurately disentangle the AGN from the SF emissions, as both contributes to the mid- and far-IR emission. Even in the case when spectral energy distribution (SED) fitting allows us to separate the two components, the results usually depend on the adopted technique and modelling. Therefore, the initial phase of the BH–galaxy co-evolution paradigm has been, so far, the most elusive and difficult to track. According to the co-evolution scenario, this heavily obscured phase should be characterised by the presence of a strong starburst and an obscured AGN, both giving a significant contribution to the mid- and far-IR emission (e.g. Page et al. Reference Page, Stevens, Ivison and Carrera2004; Vignali et al. Reference Vignali2009; Lapi et al. Reference Lapi2018).
Compton-thick (CT) AGN, that is, highly obscured AGN with column density
![]() $\log{(\text{N}_{\text{H}}/\text{cm}^{-2})} \ge 24$
, are also required to explain the spectra of the extragalactic X-ray background (XRB): their flat spectrum is needed to reproduce the hump observed at 20–30 keV in the XRB (e.g. Comastri et al. Reference Comastri, Setti, Zamorani and Hasinger1995; Gilli, Comastri, & Hasinger Reference Gilli, Comastri and Hasinger2007; Ballantyne et al. Reference Ballantyne, Draper, Madsen, Rigby and Treister2011). However, the fraction of CT-AGN derived from XRB synthesis models ranges from 10% to 30–50% (Treister, Urry, & Virani Reference Treister, Urry and Virani2009; Gilli et al. Reference Gilli, Comastri and Hasinger2007; Ueda et al. Reference Ueda, Akiyama, Hasinger, Miyaji and Watson2014; Ananna et al. Reference Ananna2019) and suffers from large uncertainties due to degeneracies between several model parameters. Although the expected number of CT-AGN is large, their detection and identification beyond the local universe are challenging and, even in the local universe, their observed fraction (
$\log{(\text{N}_{\text{H}}/\text{cm}^{-2})} \ge 24$
, are also required to explain the spectra of the extragalactic X-ray background (XRB): their flat spectrum is needed to reproduce the hump observed at 20–30 keV in the XRB (e.g. Comastri et al. Reference Comastri, Setti, Zamorani and Hasinger1995; Gilli, Comastri, & Hasinger Reference Gilli, Comastri and Hasinger2007; Ballantyne et al. Reference Ballantyne, Draper, Madsen, Rigby and Treister2011). However, the fraction of CT-AGN derived from XRB synthesis models ranges from 10% to 30–50% (Treister, Urry, & Virani Reference Treister, Urry and Virani2009; Gilli et al. Reference Gilli, Comastri and Hasinger2007; Ueda et al. Reference Ueda, Akiyama, Hasinger, Miyaji and Watson2014; Ananna et al. Reference Ananna2019) and suffers from large uncertainties due to degeneracies between several model parameters. Although the expected number of CT-AGN is large, their detection and identification beyond the local universe are challenging and, even in the local universe, their observed fraction (
![]() $\sim\!5$
–10%, e.g. Burlon et al. Reference Burlon2011; Ricci et al. Reference Ricci2015) is significantly lower than models predictions, but X-rays detection bias may be responsible of such low numbers (Burlon et al. Reference Burlon2011).
$\sim\!5$
–10%, e.g. Burlon et al. Reference Burlon2011; Ricci et al. Reference Ricci2015) is significantly lower than models predictions, but X-rays detection bias may be responsible of such low numbers (Burlon et al. Reference Burlon2011).
To select unobscured or mildly obscured AGN, one of the most effective tools is the observation in the X-ray band, thanks to the radiation coming directly from the AGN innermost regions. However, this selection loses effectiveness with the increasing column density (at N
![]() $_{\text{H}} \ge 10^{23}\,\text{cm}^{-2}$
the soft continuum is severely depressed) and, even in deep fields, only a limited fraction of the most obscured AGN has been revealed in the X-ray (e.g. Tozzi et al. Reference Tozzi2006; Lanzuisi et al. Reference Lanzuisi2013; Marchesi et al. Reference Marchesi2016; Del Moro et al. Reference Del Moro2017). Moreover, the BHAD estimation from the X-ray luminosity is strongly dependent on the bolometric correction (
$_{\text{H}} \ge 10^{23}\,\text{cm}^{-2}$
the soft continuum is severely depressed) and, even in deep fields, only a limited fraction of the most obscured AGN has been revealed in the X-ray (e.g. Tozzi et al. Reference Tozzi2006; Lanzuisi et al. Reference Lanzuisi2013; Marchesi et al. Reference Marchesi2016; Del Moro et al. Reference Del Moro2017). Moreover, the BHAD estimation from the X-ray luminosity is strongly dependent on the bolometric correction (
![]() $k_{\rm bol}$
), that allows to estimate the ‘total’ bolometric power (
$k_{\rm bol}$
), that allows to estimate the ‘total’ bolometric power (
![]() ${L}_{\rm bol}$
) of the AGN from the AGN emission in a specific band, but suffers from significant uncertainties in the
${L}_{\rm bol}$
) of the AGN from the AGN emission in a specific band, but suffers from significant uncertainties in the
![]() $k_{\rm bol}-{L}_{\rm bol}$
relation (e.g. Hopkins, Richards, & Hernquist Reference Hopkins, Richards and Hernquist2007; Lusso et al. Reference Lusso2010, Reference Lusso2012; Duras et al. Reference Duras2020). Likewise for obscured SF galaxies, the IR is an effective band in detecting these obscured AGN, thanks to the energy absorbed by the obscuring material and re-emitted at sub-mm wavelengths (e.g. Pozzi et al. Reference Pozzi2007). The effectiveness of identifying highly obscured AGN by selecting bright mid-IR sources with faint optical or near-IR emission has been shown in the past by Spitzer (e.g. Houck et al. Reference Houck2005; Weedman et al. Reference Weedman2006; Polletta et al. Reference Polletta2008) and WISE (e.g. Mateos et al. Reference Mateos2012; Assef et al. Reference Assef2013).
$k_{\rm bol}-{L}_{\rm bol}$
relation (e.g. Hopkins, Richards, & Hernquist Reference Hopkins, Richards and Hernquist2007; Lusso et al. Reference Lusso2010, Reference Lusso2012; Duras et al. Reference Duras2020). Likewise for obscured SF galaxies, the IR is an effective band in detecting these obscured AGN, thanks to the energy absorbed by the obscuring material and re-emitted at sub-mm wavelengths (e.g. Pozzi et al. Reference Pozzi2007). The effectiveness of identifying highly obscured AGN by selecting bright mid-IR sources with faint optical or near-IR emission has been shown in the past by Spitzer (e.g. Houck et al. Reference Houck2005; Weedman et al. Reference Weedman2006; Polletta et al. Reference Polletta2008) and WISE (e.g. Mateos et al. Reference Mateos2012; Assef et al. Reference Assef2013).
To be able to photometrically identify highly obscured and CT-AGN, both mid-IR and far-IR instruments are necessary, as we need to distinguish between the emission from hot dust (
![]() $T>100$
K), mostly due to reprocessed AGN emission from the dusty torus and galactic dust, and the emission from warm/cold dust (
$T>100$
K), mostly due to reprocessed AGN emission from the dusty torus and galactic dust, and the emission from warm/cold dust (
![]() $T<100$
K) dominated by the reprocessed SF emission.
$T<100$
K) dominated by the reprocessed SF emission.
A future IR cryogenic cooled space telescope may be able to deliver all of this. We investigated two different IR mission, using as ‘templates’ the proposed, now withdrawn, ESA SPace Infrared telescope for Cosmology and Astrophysics (SPICA) mission and the NASA concept study Origins Space Telescope (OST). A SPICA-like mission (described extensively in Section 2.1) with a mid-IR spectrophotometer will be able to sample the band where the peak of the CT-AGN emission is up to
![]() $z \approx 6$
and provide also low-resolution spectra, while far-IR photometric cameras will cover the wavelength range where the SF is the main contributor, thus helping in separating the two emission mechanisms. Detected sources may be followed up with SPICA SAFARI-like instruments to provide low-resolution spectra in the mid- and far-IR wavelength range up to
$z \approx 6$
and provide also low-resolution spectra, while far-IR photometric cameras will cover the wavelength range where the SF is the main contributor, thus helping in separating the two emission mechanisms. Detected sources may be followed up with SPICA SAFARI-like instruments to provide low-resolution spectra in the mid- and far-IR wavelength range up to
![]() $z \approx 3.5$
. In these spectra, high-ionisation lines, such as [Ne v] at
$z \approx 3.5$
. In these spectra, high-ionisation lines, such as [Ne v] at
![]() $14.32$
and
$14.32$
and
![]() $24.32\,\unicode[Times]{x03BC}$
m,
$24.32\,\unicode[Times]{x03BC}$
m,
![]() $[\text{Ne}$
vi] at
$[\text{Ne}$
vi] at
![]() $7.7\,\unicode[Times]{x03BC}$
m and
$7.7\,\unicode[Times]{x03BC}$
m and
![]() $[\text{O}$
iv] at
$[\text{O}$
iv] at
![]() $25.89\,\unicode[Times]{x03BC}$
m, would be signatures of AGN presence and their fluxes could be used as proxy of the AGN bolometric luminosities (e.g. Spinoglio & Malkan Reference Spinoglio and Malkan1992; García-Bernete et al. Reference García-Bernete2016; Fernández-Ontiveros et al. Reference Fernández-Ontiveros2016). Alternatively, an highly capable grating mid- and far-IR spectrometer, as the Origins Survey Spectrometer (OSS) in the OST (see Section 2.2), will be able to cover instantaneously both the hot and warm/cold dust wavelength regime, thus enabling us to distinguish between the torus and the host galaxy emission and to estimate, in a reliable way, the AGN bolometric power, the host SF, and the BH accretion rate, without the need of additional constraints from other optical-IR instruments or surveys.
$25.89\,\unicode[Times]{x03BC}$
m, would be signatures of AGN presence and their fluxes could be used as proxy of the AGN bolometric luminosities (e.g. Spinoglio & Malkan Reference Spinoglio and Malkan1992; García-Bernete et al. Reference García-Bernete2016; Fernández-Ontiveros et al. Reference Fernández-Ontiveros2016). Alternatively, an highly capable grating mid- and far-IR spectrometer, as the Origins Survey Spectrometer (OSS) in the OST (see Section 2.2), will be able to cover instantaneously both the hot and warm/cold dust wavelength regime, thus enabling us to distinguish between the torus and the host galaxy emission and to estimate, in a reliable way, the AGN bolometric power, the host SF, and the BH accretion rate, without the need of additional constraints from other optical-IR instruments or surveys.
To confirm the CT nature of sources, X-ray spectroscopy has been the most reliable method so far. Unfortunately, with the current deepest X-ray surveys, we have only scratched the surface of the obscured AGN population at
![]() $z \sim 1{-}4$
. Moreover, the identification of an AGN as CT depends strongly on the adopted analysis techniques and modeling, with different techniques giving sometimes different classifications of the same sources (e.g. Castelló-Mor et al. Reference Castelló-Mor2013). The best results have come from X-ray deep and ultradeep surveys (e.g. COSMOS, Elvis et al. Reference Elvis2009; Civano et al. Reference Civano2016, CDF-S, Giacconi et al. Reference Giacconi2002; Luo et al. Reference Luo2008; Xue et al. Reference Xue2011; Xue Reference Xue2017) that allowed to detect CT-AGN even at high redshift, but with the disadvantage of having small fields, thus low source statistics. XMM-Newton and Chandra surveys unveiled only up to few tens of candidates of CT-AGN (e.g. Comastri et al. Reference Comastri2011; Brightman & Ueda Reference Brightman and Ueda2012; Georgantopoulos et al. Reference Georgantopoulos2013; Lanzuisi et al. Reference Lanzuisi2017), while a hard X-ray mission like NuSTAR has difficulties in detecting objects beyond
$z \sim 1{-}4$
. Moreover, the identification of an AGN as CT depends strongly on the adopted analysis techniques and modeling, with different techniques giving sometimes different classifications of the same sources (e.g. Castelló-Mor et al. Reference Castelló-Mor2013). The best results have come from X-ray deep and ultradeep surveys (e.g. COSMOS, Elvis et al. Reference Elvis2009; Civano et al. Reference Civano2016, CDF-S, Giacconi et al. Reference Giacconi2002; Luo et al. Reference Luo2008; Xue et al. Reference Xue2011; Xue Reference Xue2017) that allowed to detect CT-AGN even at high redshift, but with the disadvantage of having small fields, thus low source statistics. XMM-Newton and Chandra surveys unveiled only up to few tens of candidates of CT-AGN (e.g. Comastri et al. Reference Comastri2011; Brightman & Ueda Reference Brightman and Ueda2012; Georgantopoulos et al. Reference Georgantopoulos2013; Lanzuisi et al. Reference Lanzuisi2017), while a hard X-ray mission like NuSTAR has difficulties in detecting objects beyond
![]() $z\sim 1$
, due to its sensitivity (Lansbury et al. Reference Lansbury2017a; Lansbury et al. Reference Lansbury2017b, the notable exceptions of CT-AGN at
$z\sim 1$
, due to its sensitivity (Lansbury et al. Reference Lansbury2017a; Lansbury et al. Reference Lansbury2017b, the notable exceptions of CT-AGN at
![]() $z\sim 2$
detected by Del Moro et al. Reference Del Moro2014; Zappacosta et al. Reference Zappacosta2018).
$z\sim 2$
detected by Del Moro et al. Reference Del Moro2014; Zappacosta et al. Reference Zappacosta2018).
A breakthrough in selection and identification of CT-AGN is expected with the new ESA X-ray observatory Athena (Advanced Telescope for High ENergy Astrophysics), due for launch in early 2030s. Athena, with its combination of angular resolution, field of view, and collecting area at
![]() $\sim\!1\,$
keV, is the ideal instrument to perform X-ray surveys and will be more than two orders of magnitude faster than Chandra or XMM-Newton (Nandra et al. Reference Nandra2013). The excellent spectral capabilities of Athena WFI for surveys will yield samples of the most heavily obscured AGN up to redshifts
$\sim\!1\,$
keV, is the ideal instrument to perform X-ray surveys and will be more than two orders of magnitude faster than Chandra or XMM-Newton (Nandra et al. Reference Nandra2013). The excellent spectral capabilities of Athena WFI for surveys will yield samples of the most heavily obscured AGN up to redshifts
![]() $z=4$
and up to 100 times larger than is currently possible. Since
$z=4$
and up to 100 times larger than is currently possible. Since
![]() $\text{L}_{\text{X-ray}} \gtrsim 10^{42}\,\mathrm{erg\,s}^{-1}$
are commonly associated with AGN activity, Athena will also be invaluable in quickly identifying moderate- and high-luminous AGN, especially in cases where we can not distinguish between the torus mid-IR emission and the host galaxy contribution from SED fitting analysis.
$\text{L}_{\text{X-ray}} \gtrsim 10^{42}\,\mathrm{erg\,s}^{-1}$
are commonly associated with AGN activity, Athena will also be invaluable in quickly identifying moderate- and high-luminous AGN, especially in cases where we can not distinguish between the torus mid-IR emission and the host galaxy contribution from SED fitting analysis.
The planned launch date for Athena is
![]() ${\gtrsim}2030$
. Having, in the same years, a new IR mission dedicated (also) to survey high-z galaxy and AGN would be an extraordinary opportunity to study obscured accretion and to characterise AGN up to high redshift. A possible example of such mission would have been SPICA, but also the NASA concept OST for an
${\gtrsim}2030$
. Having, in the same years, a new IR mission dedicated (also) to survey high-z galaxy and AGN would be an extraordinary opportunity to study obscured accretion and to characterise AGN up to high redshift. A possible example of such mission would have been SPICA, but also the NASA concept OST for an
![]() $4.5\,$
K cooled IR space observatory, which has a proposed launch date of
$4.5\,$
K cooled IR space observatory, which has a proposed launch date of
![]() $\sim\!2035$
and similar survey strategy and wavelength coverage as SPICA. Having data at X-ray and IR wavelengths will be the key to accurately reconstruct the accretion luminosity across cosmic time up to very high redshift (
$\sim\!2035$
and similar survey strategy and wavelength coverage as SPICA. Having data at X-ray and IR wavelengths will be the key to accurately reconstruct the accretion luminosity across cosmic time up to very high redshift (
![]() $z \approx 6$
). The search for the elusive CT-AGN may decisively benefit from the synergies between Athena and future IR mission: while a SPICA-like telescope and the OST should be able to effectively detect the majority of them (even those too obscured to be detected in X-rays), the X-ray spectra provided by Athena will be invaluable to confirm their CT-nature, even in paucity of photons, for a large fraction of them.
$z \approx 6$
). The search for the elusive CT-AGN may decisively benefit from the synergies between Athena and future IR mission: while a SPICA-like telescope and the OST should be able to effectively detect the majority of them (even those too obscured to be detected in X-rays), the X-ray spectra provided by Athena will be invaluable to confirm their CT-nature, even in paucity of photons, for a large fraction of them.
The goal of this paper is to study the synergies between Athena and future IR surveys in searching and identifying AGN, with a particular focus on the most obscured ones. We will show how the search for these elusive CT-AGN, very difficult to identify and characterise with the current instruments, can benefit from a combined use of IR and X-ray data. In Section 2, we give a brief description of the SPICA and OST instruments and planned surveys and a comparison with the Athena surveys. The simulation of the intrinsic AGN prediction obtained from the XRB synthesis models are presented in Section 3, while the number of those which will be detected by Athena are reported in Section 4. In Section 5, we present the optical-to-far-IR SED used to predict the AGN emission and their detectability with OST and SPICA-like mission. The prediction of the number of AGN that will be detected by the IR surveys, as well as the synergies with Athena that we can exploit to study them, are reported in Section 6. In Section 7, we present our conclusions.
Throughout this paper, we adopt the following cosmological parameters: H
![]() $_0 = 70\, \text{km}\, \text{s}^{-1}\, \text{Mpc}^{-1}$
,
$_0 = 70\, \text{km}\, \text{s}^{-1}\, \text{Mpc}^{-1}$
,
![]() $\Omega_{{M}} = 0.3$
, and
$\Omega_{{M}} = 0.3$
, and
![]() $\Omega_{\Lambda} = 0.7$
(Spergel et al. Reference Spergel2003).
$\Omega_{\Lambda} = 0.7$
(Spergel et al. Reference Spergel2003).
2. Instruments and surveys
2.1. SPICA
SPICA was a joint European-Japanese project to develop a new generation cryogenic infrared space telescope, with the early design dating back to more than two decades ago (e.g. Nakagawa et al. Reference Nakagawa, Bely and Breckinridge1998, Reference Nakagawa2014; Swinyard et al. Reference Swinyard2009). Here we discuss the SMI and B-BOP instruments as it were designed during the ESA M5 selection process and a SPICA-like survey strategy.
2.1.1. SMI
SMI is composed of the four channels, SMI-CAM, LR, MR, and HR. In this paper, we consider SMI-CAM and SMI-LR that work simultaneously. SMI-CAM is a mid-IR slit viewer photometric camera that covers the 30–
![]() $37\,\unicode[Times]{x03BC}$
m range and provides
$37\,\unicode[Times]{x03BC}$
m range and provides
![]() $34\,\unicode[Times]{x03BC}$
m broad-band images with a field of view of
$34\,\unicode[Times]{x03BC}$
m broad-band images with a field of view of
![]() $10'\times 12'$
(with the exclusion of the four slits used by the spectrometer). SMI-LR is a wide field-of-view multi-slit prism spectrometer, composed of four long slits of 10′ in length and
$10'\times 12'$
(with the exclusion of the four slits used by the spectrometer). SMI-LR is a wide field-of-view multi-slit prism spectrometer, composed of four long slits of 10′ in length and
![]() $3.7''$
in width. It has a resolution of
$3.7''$
in width. It has a resolution of
![]() $R = 50$
–120 and allows spectroscopic surveys in the 17–
$R = 50$
–120 and allows spectroscopic surveys in the 17–
![]() $36\,\unicode[Times]{x03BC}$
m wavelength range. The SMI-CAM provides photometric scientific data and is invaluable in accurately determining the position of the slits on the sky for pointing reconstruction in creating spectral maps. We refer to Kaneda et al. (Reference Kaneda2017) for further instrument specifications and survey strategies.
$36\,\unicode[Times]{x03BC}$
m wavelength range. The SMI-CAM provides photometric scientific data and is invaluable in accurately determining the position of the slits on the sky for pointing reconstruction in creating spectral maps. We refer to Kaneda et al. (Reference Kaneda2017) for further instrument specifications and survey strategies.
2.1.2. B-BOP
The B-BOP polarimetric instrument allows simultaneous imaging observations in three bands, centered at 70, 200, and 350
![]() $\,\unicode[Times]{x03BC}$
m, over an instantaneous field of view from
$\,\unicode[Times]{x03BC}$
m, over an instantaneous field of view from
![]() $ 1.8'\times 1.8'$
to
$ 1.8'\times 1.8'$
to
![]() $ 2.7'\times2.7'$
at Full Width Half Maximum (FWHM) resolutions of 6′′, 17′′, and 30′′, respectively. B-BOP is two to three orders of magnitude more sensitive than current or planned far-IR/submillimeter polarimeters, for example, SHARP (Li et al. Reference Li, Dowell, Kirby, Novak and Vaillancourt2008), HAWC + (SOFIA) (Dowell et al. Reference Dowell1998), and BLAST-TNG (Galitzki et al. Reference Galitzki2014). It provides wide field
$ 2.7'\times2.7'$
at Full Width Half Maximum (FWHM) resolutions of 6′′, 17′′, and 30′′, respectively. B-BOP is two to three orders of magnitude more sensitive than current or planned far-IR/submillimeter polarimeters, for example, SHARP (Li et al. Reference Li, Dowell, Kirby, Novak and Vaillancourt2008), HAWC + (SOFIA) (Dowell et al. Reference Dowell1998), and BLAST-TNG (Galitzki et al. Reference Galitzki2014). It provides wide field
![]() $70-350\,\unicode[Times]{x03BC}$
m polarimetric images in Stokes Q and U of comparable quality (in terms of resolution, signal-to-noise ratio, and both intensity and spatial dynamic ranges) to Herschel images in Stokes I. More details about the B-BOP instrument are in Rodriguez et al. (Reference Rodriguez2018) and André et al. (Reference André2019).
$70-350\,\unicode[Times]{x03BC}$
m polarimetric images in Stokes Q and U of comparable quality (in terms of resolution, signal-to-noise ratio, and both intensity and spatial dynamic ranges) to Herschel images in Stokes I. More details about the B-BOP instrument are in Rodriguez et al. (Reference Rodriguez2018) and André et al. (Reference André2019).
2.1.3. Surveys with SMI
Hereafter, we consider two reference blind spectroscopic surveys:
-
a
 $1\mathrm{deg}^2$
ultradeep survey with a total observational time of
$1\mathrm{deg}^2$
ultradeep survey with a total observational time of
 $600\,$
h, an SMI-CAM
$600\,$
h, an SMI-CAM
 $5\,\sigma$
sensitivity of
$5\,\sigma$
sensitivity of
 ${\approx}3\,\unicode[Times]{x03BC}$
Jy and an SMI-LR
${\approx}3\,\unicode[Times]{x03BC}$
Jy and an SMI-LR
 $5\,\sigma$
sensitivities (high-background case) of
$5\,\sigma$
sensitivities (high-background case) of
 ${\approx}50\,\unicode[Times]{x03BC}$
Jy at
${\approx}50\,\unicode[Times]{x03BC}$
Jy at
 $20\,\unicode[Times]{x03BC}$
m,
$20\,\unicode[Times]{x03BC}$
m,
 ${\approx}110\,\unicode[Times]{x03BC}$
Jy at
${\approx}110\,\unicode[Times]{x03BC}$
Jy at
 $30\,\unicode[Times]{x03BC}$
m, and a line sensitivity of
$30\,\unicode[Times]{x03BC}$
m, and a line sensitivity of
 ${\approx}9.2\times10^{-20}\,\mathrm{W m}^{-2}$
(this survey configuration corresponds to the Kaneda et al. Reference Kaneda2017 deep survey);
${\approx}9.2\times10^{-20}\,\mathrm{W m}^{-2}$
(this survey configuration corresponds to the Kaneda et al. Reference Kaneda2017 deep survey); -
a
 $15\,\mathrm{deg}^2$
deep survey with a total observational time of
$15\,\mathrm{deg}^2$
deep survey with a total observational time of
 $600\,$
h, an SMI-CAM
$600\,$
h, an SMI-CAM
 $5\,\sigma$
sensitivity of
$5\,\sigma$
sensitivity of
 ${\approx}13\,\unicode[Times]{x03BC}$
Jy and an
${\approx}13\,\unicode[Times]{x03BC}$
Jy and an
 $5\,\sigma$
SMI-LR sensitivities (high-background case) of
$5\,\sigma$
SMI-LR sensitivities (high-background case) of
 ${\approx}160\,\unicode[Times]{x03BC}$
Jy at
${\approx}160\,\unicode[Times]{x03BC}$
Jy at
 $20\,\unicode[Times]{x03BC}$
m,
$20\,\unicode[Times]{x03BC}$
m,
 ${\approx}380\,\unicode[Times]{x03BC}$
Jy at
${\approx}380\,\unicode[Times]{x03BC}$
Jy at
 $30\,\unicode[Times]{x03BC}$
m, and a line sensitivity of
$30\,\unicode[Times]{x03BC}$
m, and a line sensitivity of
 ${\approx}33\times10^{-20}\,\mathrm{Wm}^{-2}$
(this survey has the same depth of the Kaneda et al. Reference Kaneda2017 shallow survey, although over a larger area).
${\approx}33\times10^{-20}\,\mathrm{Wm}^{-2}$
(this survey has the same depth of the Kaneda et al. Reference Kaneda2017 shallow survey, although over a larger area).
2.2. The Origins Space Telescope
The OST (Battersby et al. Reference Battersby2018; Meixner et al. Reference Meixner2019) is a concept study for a Far-Infrared Surveyor mission, the subject of one of four science and technology definition studies supported by NASA for the 2020 Astronomy and Astrophysics Decadal Survey. The OST is being designed with the aim of covering a large area of the sky, thus allowing to search for rare objects at low and high redshifts.
OST is composed of a
![]() $5.9\,$
m-diameter telescope with a Spitzer-like architecture, actively cooled down to
$5.9\,$
m-diameter telescope with a Spitzer-like architecture, actively cooled down to
![]() $4.5\,$
K. It is designed with three onboard instruments: the OSS to cover the 25–
$4.5\,$
K. It is designed with three onboard instruments: the OSS to cover the 25–
![]() $588\,\unicode[Times]{x03BC}$
m wavelength range instantaneously at
$588\,\unicode[Times]{x03BC}$
m wavelength range instantaneously at
![]() $R=300$
, Mid-Infrared Spectrometer Camera Transit (MISC-T) a
$R=300$
, Mid-Infrared Spectrometer Camera Transit (MISC-T) a
![]() $2.8$
–
$2.8$
–
![]() $20\,\unicode[Times]{x03BC}$
m transit spectrometer, and the Far-infrared Imager and Polarimeter (FIP), that delivers imaging or polarimetry at 50 and
$20\,\unicode[Times]{x03BC}$
m transit spectrometer, and the Far-infrared Imager and Polarimeter (FIP), that delivers imaging or polarimetry at 50 and
![]() $250\,\unicode[Times]{x03BC}$
m. In this paper, we take into consideration primarily the OSS instrument, as it is perfectly suited for detecting and characterising AGN in blind surveys.
$250\,\unicode[Times]{x03BC}$
m. In this paper, we take into consideration primarily the OSS instrument, as it is perfectly suited for detecting and characterising AGN in blind surveys.
2.2.1. OSS
The OSS is a
![]() $R=300$
spectrometer covering the full 25–
$R=300$
spectrometer covering the full 25–
![]() $588\,\unicode[Times]{x03BC}$
m wavelength range instantaneously, using six logarithmically spaced grating modules. True 3D spectral mapping is performed thanks to the 30–100 spatial beams that each module couples. Higher spectral resolution can be achieved by inserting into the light-path two mirrors that divert the light into interferometer optics allowing a
$588\,\unicode[Times]{x03BC}$
m wavelength range instantaneously, using six logarithmically spaced grating modules. True 3D spectral mapping is performed thanks to the 30–100 spatial beams that each module couples. Higher spectral resolution can be achieved by inserting into the light-path two mirrors that divert the light into interferometer optics allowing a
![]() $R=43\,000$
resolution, keeping the full spectral range but working only on single pointing (i.e. losing the survey capabilities). Even higher
$R=43\,000$
resolution, keeping the full spectral range but working only on single pointing (i.e. losing the survey capabilities). Even higher
![]() $R=300\,000$
spectral resolution can be achieved using an insertable etalon, further restricting the field of view (FoV) and reducing the spectral range to 100–
$R=300\,000$
spectral resolution can be achieved using an insertable etalon, further restricting the field of view (FoV) and reducing the spectral range to 100–
![]() $200\,\unicode[Times]{x03BC}$
m. As in this paper we focus on detecting AGN in surveys, we take into consideration only the base
$200\,\unicode[Times]{x03BC}$
m. As in this paper we focus on detecting AGN in surveys, we take into consideration only the base
![]() $R=300$
spectroscopy mode.
$R=300$
spectroscopy mode.
The six OSS bands cover the 25–44, 42–74, 71–124, 119–208, 200–350, and 336–
![]() $589\,\unicode[Times]{x03BC}$
m wavelength ranges, with beam sizes of 1.41, 2.38, 4.0, 6.78, 11.3, and 19.0 arcsec and
$589\,\unicode[Times]{x03BC}$
m wavelength ranges, with beam sizes of 1.41, 2.38, 4.0, 6.78, 11.3, and 19.0 arcsec and
![]() $1\,$
h
$1\,$
h
![]() $5\,\sigma$
sensitivities (
$5\,\sigma$
sensitivities (
![]() $R=300$
) of 22, 28, 40, 104, 104, and 338
$R=300$
) of 22, 28, 40, 104, 104, and 338
![]() $\,\unicode[Times]{x03BC}$
Jy. With the current OSS specs, an improvement of more than a factor
$\,\unicode[Times]{x03BC}$
Jy. With the current OSS specs, an improvement of more than a factor
![]() $1\,000$
in sensitivity is expected with respect to already flown far-IR observatories (SOFIA, Herscel-SPIRE, and Herschel-PACS). We refer to Meixner et al. (Reference Meixner2019) for further instrument specifications.
$1\,000$
in sensitivity is expected with respect to already flown far-IR observatories (SOFIA, Herscel-SPIRE, and Herschel-PACS). We refer to Meixner et al. (Reference Meixner2019) for further instrument specifications.
Table 1. Parameters of the SPICA, Athena, and OST surveys. The time per field
![]() $t_{\text{field}}$
are pure integration times, without over-heads. The sensitivities are computed at
$t_{\text{field}}$
are pure integration times, without over-heads. The sensitivities are computed at
![]() $5 \sigma$
. The SPICA
$5 \sigma$
. The SPICA
![]() $R=150$
sensitivities are reported at
$R=150$
sensitivities are reported at
![]() $20\,\unicode[Times]{x03BC}$
m. The B-BOP sensitivities refer only to the
$20\,\unicode[Times]{x03BC}$
m. The B-BOP sensitivities refer only to the
![]() $70\,\unicode[Times]{x03BC}$
m channel, while those for the OST refer to channel 1 and channel 6. In this table, the Athena survey strategy is simplified, as the deep survey encompasses also the ultradeep pointings and the shallow survey will comprehend also the deep pointings. The Athena sensitivities refer to the 2–10 keV band. The surveys investigated and the naming scheme used in this work are summarised in Table 2.
$70\,\unicode[Times]{x03BC}$
m channel, while those for the OST refer to channel 1 and channel 6. In this table, the Athena survey strategy is simplified, as the deep survey encompasses also the ultradeep pointings and the shallow survey will comprehend also the deep pointings. The Athena sensitivities refer to the 2–10 keV band. The surveys investigated and the naming scheme used in this work are summarised in Table 2.

2.2.2. Survey with OSS
For OST, we consider two blind blank field spectroscopic surveys as described in Meixner et al. (Reference Meixner2019):
-
a
 $0.5\,\mathrm{deg}^2$
deep survey with an observational time of
$0.5\,\mathrm{deg}^2$
deep survey with an observational time of
 ${\approx}1\,000\,$
h, a
${\approx}1\,000\,$
h, a
 $R=4$
,
$R=4$
,
 $5\,\sigma$
sensitivity of 4.5, 5.8, 8.4, 21.8, 21.8, and 70.9
$5\,\sigma$
sensitivity of 4.5, 5.8, 8.4, 21.8, 21.8, and 70.9
 $\,\unicode[Times]{x03BC}$
Jy (for channel 1–6), and a
$\,\unicode[Times]{x03BC}$
Jy (for channel 1–6), and a
 $R=300$
$R=300$
 $5\,\sigma$
sensitivity of 39, 50, 72, 189, 189, and 614
$5\,\sigma$
sensitivity of 39, 50, 72, 189, 189, and 614
 $\,\unicode[Times]{x03BC}$
Jy;
$\,\unicode[Times]{x03BC}$
Jy; -
a
 $20\,\mathrm{deg}^2$
wide survey with an observational time of
$20\,\mathrm{deg}^2$
wide survey with an observational time of
 ${\approx}1\,000\,$
h, a
${\approx}1\,000\,$
h, a
 $R=4$
,
$R=4$
,
 $5\,\sigma$
sensitivity of 30, 39, 56, 145, 145, and 473
$5\,\sigma$
sensitivity of 30, 39, 56, 145, 145, and 473
 $\,\unicode[Times]{x03BC}$
Jy (for channel 1–6), and a
$\,\unicode[Times]{x03BC}$
Jy (for channel 1–6), and a
 $R=300$
$R=300$
 $5\,\sigma$
sensitivity of 262, 336, 483, 1 260, 1 260, and 4 094
$5\,\sigma$
sensitivity of 262, 336, 483, 1 260, 1 260, and 4 094
 $\,\unicode[Times]{x03BC}$
Jy.
$\,\unicode[Times]{x03BC}$
Jy.
2.3. Athena
Athena Footnote a (Barcons et al. Reference Barcons2017) is the X-ray observatory mission selected by ESA, within its Cosmic Vision programme, to address the Hot and Energetic Universe scientific theme. It is the second L(large)-class mission within that programme and is due for adoption in late 2022 and launch in early 2030s.
Athena will consist of a single large-aperture grazing incidence X-ray telescope, utilising a novel technology (high-performance silicon pore optics) developed in Europe, with 12-m focal length and 5-arcsec half energy width (HEW) on-axis angular resolution, degrading gradually to less than 10 arcsec at 30 arcmin off-axis (Bavdaz et al. Reference Bavdaz2018). There will be two instruments in the focal plane. One is the Wide Field Imager (WFI)Footnote b (Meidinger, Nandra, & Plattner Reference Meidinger, Nandra and Plattner2018) providing simultaneous sensitive wide field imaging and spectroscopy (FWHM
![]() $\leq 170$
eV at 7 keV) and high count rate capability (
$\leq 170$
eV at 7 keV) and high count rate capability (
![]() $>$
90% throughput and
$>$
90% throughput and
![]() $<$
1% pile-up for 1 Crab) over the 0.2–15 keV energy range. This is achieved through two sets of silicon-based detectors using DEPFET Active Pixel Sensor technology: the Large Detector Array is a mosaic of
$<$
1% pile-up for 1 Crab) over the 0.2–15 keV energy range. This is achieved through two sets of silicon-based detectors using DEPFET Active Pixel Sensor technology: the Large Detector Array is a mosaic of
![]() $2 \times 2$
arrays spanning a
$2 \times 2$
arrays spanning a
![]() $\sim\!40 \times 40\,\text{arcmin}^2$
FoV oversampling the Point Spread Function (PSF) by more than a factor of 2 and the Fast Detector is a single array optimised for high count rate applications.
$\sim\!40 \times 40\,\text{arcmin}^2$
FoV oversampling the Point Spread Function (PSF) by more than a factor of 2 and the Fast Detector is a single array optimised for high count rate applications.
The other instrument is the X-ray Integral Field Unit (X-IFU)Footnote c (Barret et al. Reference Barret2018) delivering simultaneous spatially resolved (5 arcsec pixels) high-resolution X-ray spectroscopy (FWHM
![]() $<$
2.5 eV below 7 keV) over a limited field of view (
$<$
2.5 eV below 7 keV) over a limited field of view (
![]() $\sim$
5 arcmin equivalent diameter) over the 0.2–12 keV energy range, with high count rate capability (10 eV spectral resolution at 1 Crab intensities with low pile-up and
$\sim$
5 arcmin equivalent diameter) over the 0.2–12 keV energy range, with high count rate capability (10 eV spectral resolution at 1 Crab intensities with low pile-up and
![]() $>$
50% throughput). This performance is based on a large format array of superconducting molybdenum-gold Transition Edge Sensors coupled to absorbers made of gold and bismuth, cooled at
$>$
50% throughput). This performance is based on a large format array of superconducting molybdenum-gold Transition Edge Sensors coupled to absorbers made of gold and bismuth, cooled at
![]() $\sim$
90 mK inside a nested set of cryostats.
$\sim$
90 mK inside a nested set of cryostats.
2.3.1. Surveys with Athena
Some of the core science objectives of Athena
Footnote d (e.g. finding distant evolved groups of galaxies at
![]() $z>2$
, complete the census for high-redshift and heavily obscured AGN) require performing surveys of the X-ray sky with the WFI. These surveys are expected to take a significant part of the observation time during the 4 years of the nominal mission lifetime. At the time of writing, the nominal number of pointings and exposure times (the so-called ‘Tier 2 post-CORE strategy’) includes an ‘ultradeep’ layer (
$z>2$
, complete the census for high-redshift and heavily obscured AGN) require performing surveys of the X-ray sky with the WFI. These surveys are expected to take a significant part of the observation time during the 4 years of the nominal mission lifetime. At the time of writing, the nominal number of pointings and exposure times (the so-called ‘Tier 2 post-CORE strategy’) includes an ‘ultradeep’ layer (
![]() $4 \times 1\,400$
ks), a ‘deep’ layer (
$4 \times 1\,400$
ks), a ‘deep’ layer (
![]() $3 \times 980$
ks
$3 \times 980$
ks
![]() $+\, 7 \times 840$
ks), and a ‘shallow’ layer (106
$+\, 7 \times 840$
ks), and a ‘shallow’ layer (106
![]() $\times$
84 ks) (see Table 1). Each pointing covers
$\times$
84 ks) (see Table 1). Each pointing covers
![]() $\sim\!0.4\ \mathrm{deg}^2$
, so the total area of each layer is 1.6, 4, and
$\sim\!0.4\ \mathrm{deg}^2$
, so the total area of each layer is 1.6, 4, and
![]() $42.5\ \mathrm{deg}^2$
, respectively. The exact places and geometries (single pointings vs mosaics) of those layers will of course be determined at a later stage by the international astronomical community through the guaranteed time and open time, but they are expected to include regions of the sky with substantial multi-wavelength coverage. An initial estimate is encapsulated in the Athena Mock Observing Plan (MOP).
$42.5\ \mathrm{deg}^2$
, respectively. The exact places and geometries (single pointings vs mosaics) of those layers will of course be determined at a later stage by the international astronomical community through the guaranteed time and open time, but they are expected to include regions of the sky with substantial multi-wavelength coverage. An initial estimate is encapsulated in the Athena Mock Observing Plan (MOP).
2.4. Surveys comparison
Athena WFI, OST OSS, and SPICA SMI have planned survey with different layers of depth and area. In this work, we compared the different layers, matching them to have similar areas as much as possible. As we compared the expected number of sources per
![]() $\mathrm{deg}^2$
for all the surveys and investigated the fraction of sources that may be detected, the exact area coverage is not critical. We investigate the capabilities of the observatories considering a DEEP survey (comparing the SPICA ultradeep survey with the Athena ultradeep survey and the OST deep survey), and a WIDE survey (composed of the SPICA deep survey, the Athena shallow survey, and the OST wide survey). Table 1 summarises the main parameters of all the SPICA, OSS, and Athena surveys, while Table 2 reports the naming scheme used in this work.
$\mathrm{deg}^2$
for all the surveys and investigated the fraction of sources that may be detected, the exact area coverage is not critical. We investigate the capabilities of the observatories considering a DEEP survey (comparing the SPICA ultradeep survey with the Athena ultradeep survey and the OST deep survey), and a WIDE survey (composed of the SPICA deep survey, the Athena shallow survey, and the OST wide survey). Table 1 summarises the main parameters of all the SPICA, OSS, and Athena surveys, while Table 2 reports the naming scheme used in this work.
3. Simulation of the intrinsic AGN counts from XRB synthesis model
We have estimated the ‘intrinsic’ AGN number as a function of the redshift z, 2–10 keV intrinsic X-ray luminosities
![]() $\text{L}_{\text{x}}$
, and intrinsic column density
$\text{L}_{\text{x}}$
, and intrinsic column density
![]() $\text{N}_{\text{H}}$
based on the Gilli et al. (Reference Gilli, Comastri and Hasinger2007) XRB synthesis model. We have started by dividing the
$\text{N}_{\text{H}}$
based on the Gilli et al. (Reference Gilli, Comastri and Hasinger2007) XRB synthesis model. We have started by dividing the
![]() $(z,\text{L}_{\text{x}},\text{N}_{\text{H}})$
space in bins, with 21 z bins
$(z,\text{L}_{\text{x}},\text{N}_{\text{H}})$
space in bins, with 21 z bins
![]() $\in [0,10]$
, 18
$\in [0,10]$
, 18
![]() $\text{L}_{\text{x}}$
bins with
$\text{L}_{\text{x}}$
bins with
![]() $\text{L}_{\text{x}}\in [10^{42},1.5\times10^{48}]\ \mathrm{erg\ s}^{-1}$
and 6
$\text{L}_{\text{x}}\in [10^{42},1.5\times10^{48}]\ \mathrm{erg\ s}^{-1}$
and 6
![]() $\text{N}_{\text{H}}$
bins with
$\text{N}_{\text{H}}$
bins with
![]() $\log(\text{N}_{\text{H}}/\text{cm}^{-2})\in [20,26]$
. We, then, make use of the software POMPAFootnote e to get the
$\log(\text{N}_{\text{H}}/\text{cm}^{-2})\in [20,26]$
. We, then, make use of the software POMPAFootnote e to get the
![]() $\log{N({>}S)}$
source density in each of those bins, with S being the 2–10 keV source flux.
$\log{N({>}S)}$
source density in each of those bins, with S being the 2–10 keV source flux.
From the
![]() $N({>}S)$
, we also obtained the total intensity of each bin (energy received per unit area, unit time, and unit sky area). Instead of the composite power law plus reflection spectral model in Gilli et al. (Reference Gilli, Comastri and Hasinger2007), we have adopted here a torus model from Brightman & Nandra (Reference Brightman and Nandra2011) with photon index
$N({>}S)$
, we also obtained the total intensity of each bin (energy received per unit area, unit time, and unit sky area). Instead of the composite power law plus reflection spectral model in Gilli et al. (Reference Gilli, Comastri and Hasinger2007), we have adopted here a torus model from Brightman & Nandra (Reference Brightman and Nandra2011) with photon index
![]() $\Gamma=1.9$
, aperture angle 30 deg and inclination 80 deg. We have also included an additional scattering component modelled with a power-law with the same photon index and normalisation equal to 1% of that of the primary emission.
$\Gamma=1.9$
, aperture angle 30 deg and inclination 80 deg. We have also included an additional scattering component modelled with a power-law with the same photon index and normalisation equal to 1% of that of the primary emission.
In addition, we also included ‘normal’ galaxies using the galaxy
![]() $\log N- \log S$
curve of Lehmer et al. (Reference Lehmer2012) and a power-law spectral shape with
$\log N- \log S$
curve of Lehmer et al. (Reference Lehmer2012) and a power-law spectral shape with
![]() $\Gamma=1$
(the median value for the 332 sources with spectral slope not based on upper limits in Lehmer et al. Reference Lehmer2012) and
$\Gamma=1$
(the median value for the 332 sources with spectral slope not based on upper limits in Lehmer et al. Reference Lehmer2012) and
![]() $S\in[5\times 10^{-20}, 5\times 10^{-16}]\ \mathrm{erg\ cm}^{-2}\ \mathrm{s}^{-1}$
.
$S\in[5\times 10^{-20}, 5\times 10^{-16}]\ \mathrm{erg\ cm}^{-2}\ \mathrm{s}^{-1}$
.
Table 2. Reference surveys used in this work. The surveys composing the reference surveys were matched in similar area coverage.

Physical fluxes are converted to counts using the latest (at the time of writing) set of FoV-averaged without filter WFI matricesFootnote f using xspecFootnote g (Arnaud Reference Arnaud, Jacoby and Barnes1996).
4. Predictions of Athena source counts
When observed by the WFI on board Athena, all the sources above are seen against a ‘background’ which includes several componentsFootnote h , Footnote i:
-
Particle background: due to cosmic rays impacting the detector and the surrounding structure. It is assumed to contribute
 $6\times 10^{-4}\ \mathrm{cts\ keV}^{-1}\ \mathrm{s}^{-1} \mathrm{arcmin}^2$
with a flat power-law spectrum characterised by a spectral index of
$6\times 10^{-4}\ \mathrm{cts\ keV}^{-1}\ \mathrm{s}^{-1} \mathrm{arcmin}^2$
with a flat power-law spectrum characterised by a spectral index of
 $\Gamma=0$
.
$\Gamma=0$
. -
Diffuse galactic XRB: it is assumed to be uniform and to have the spectral shape and intensity from McCammon et al. (Reference McCammon2002), which includes two thermal components, one unabsorbed representing emission from the Local Hot Bubble and one with foreground absorption by our own Galaxy representing emission from the hot galactic halo, in xspec parlance: apec
 $_1$
+ phabs (apec
$_1$
+ phabs (apec
 $_2$
) with
$_2$
) with
 $kT_1 = 0.099$
keV and
$kT_1 = 0.099$
keV and
 $kT_2 = 0.225$
keV and respective apec normalisations of
$kT_2 = 0.225$
keV and respective apec normalisations of
 $1.7 \times 10^{-6}$
and
$1.7 \times 10^{-6}$
and
 $7.3 \times 10^{-7}$
, corresponding to
$7.3 \times 10^{-7}$
, corresponding to
 $1\ \mathrm{arcmin}^2$
; the column density for the galactic absorption is assumed to be the same as for extragalactic sources (see below).
$1\ \mathrm{arcmin}^2$
; the column density for the galactic absorption is assumed to be the same as for extragalactic sources (see below). -
XRB: due to the integrated emission of the above AGN and galaxy populations. It is assumed to have intensity and power-law spectral shape from McCammon et al. (Reference McCammon2002) but with
 $\Gamma=1.45$
and normalisation
$\Gamma=1.45$
and normalisation
 $10^{-6}\ \mathrm{photons\ s}^{-1}\mathrm{cm}^{-2}\mathrm{keV}^{-1}$
, again normalised to
$10^{-6}\ \mathrm{photons\ s}^{-1}\mathrm{cm}^{-2}\mathrm{keV}^{-1}$
, again normalised to
 $ 1\ \mathrm{arcmin}^2$
.
$ 1\ \mathrm{arcmin}^2$
. -
Stray light: X-ray photons from the two previous components, coming from outside the FoV but impacting the WFI after a single reflection on the mirror. We have modelled it by averaging the contribution of the two previous components over the full WFI FoV and fitting it with two thermal components and a power-law, with the same temperatures and photon index but with free relative normalisations.
All extragalactic components are assumed to undergo absorption by gas in our own Galaxy with hydrogen column density of
![]() $\text{N}_{\text{H}}=1.8\times 10^{20}\,\text{cm}^{-2}$
, which is the average galactic column density of the estimated survey pointings in the MOP and coincides with the foreground column density in McCammon et al. (Reference McCammon2002).
$\text{N}_{\text{H}}=1.8\times 10^{20}\,\text{cm}^{-2}$
, which is the average galactic column density of the estimated survey pointings in the MOP and coincides with the foreground column density in McCammon et al. (Reference McCammon2002).
Depending on the
![]() $(z,\text{L}_{\text{x}},\text{N}_{\text{H}})$
and the exposure time, a fraction
$(z,\text{L}_{\text{x}},\text{N}_{\text{H}})$
and the exposure time, a fraction
![]() $f_{\rm det}$
of the sources in each of the bins, described above, will be detected, contributing to resolve a fraction of the full intensity of the extragalactic XRB, thus lowering the remaining (unresolved) background. For each of the exposure time values of the survey layers, we have determined the resolved fraction iteratively starting from an initial fiducial value of 80% and
$f_{\rm det}$
of the sources in each of the bins, described above, will be detected, contributing to resolve a fraction of the full intensity of the extragalactic XRB, thus lowering the remaining (unresolved) background. For each of the exposure time values of the survey layers, we have determined the resolved fraction iteratively starting from an initial fiducial value of 80% and
![]() $f_{\rm det}$
is also determined for each bin in each iteration. To decide whether a source is detected above the background, we have used Cash statistic C (Cash Reference Cash1979): calling T the total source + background counts, B the background counts, and t the exposure time, the mode (most probable value) of the source counts is
$f_{\rm det}$
is also determined for each bin in each iteration. To decide whether a source is detected above the background, we have used Cash statistic C (Cash Reference Cash1979): calling T the total source + background counts, B the background counts, and t the exposure time, the mode (most probable value) of the source counts is
![]() $\hat s=\max(0,T-B)$
. For a 5
$\hat s=\max(0,T-B)$
. For a 5
![]() $\sigma$
detection for a single free parameter (s), we required that the Cash statistic improves by
$\sigma$
detection for a single free parameter (s), we required that the Cash statistic improves by
![]() $\Delta C=25$
between
$\Delta C=25$
between
![]() $s=0$
(i.e. no source) and
$s=0$
(i.e. no source) and
![]() $s=\hat s$
. For each bin, 100 sources are simulated at the bin centre and
$s=\hat s$
. For each bin, 100 sources are simulated at the bin centre and
![]() $f_{\rm det}$
is the fraction of those sources that are detected. It turns out that the resolved fraction is around 80% and varies a few percent for exposure times above
$f_{\rm det}$
is the fraction of those sources that are detected. It turns out that the resolved fraction is around 80% and varies a few percent for exposure times above
![]() $\sim$
10 ks. In order to estimate the source + background and the background counts, we have assumed a circular extraction area of radius 5.7 arcsec, which is the WFI FoV-weighted average of the Athena mirror HEW.
$\sim$
10 ks. In order to estimate the source + background and the background counts, we have assumed a circular extraction area of radius 5.7 arcsec, which is the WFI FoV-weighted average of the Athena mirror HEW.
4.1. Athena source characterisation
By their own nature, X-ray detectors work in photon-counting mode. One of the consequences of this is that they all are ‘Integral Field Units’, providing spectra for all detected sources. For Athena, this ranges from the superb
![]() $\sim$
2.5 eV resolution of X-IFU to the modest (but good for a Si-based detector)
$\sim$
2.5 eV resolution of X-IFU to the modest (but good for a Si-based detector)
![]() $170\,$
eV resolution at
$170\,$
eV resolution at
![]() $7\,$
keV of WFI. We have simulated 100 spectra at the ‘centres’ of each of the
$7\,$
keV of WFI. We have simulated 100 spectra at the ‘centres’ of each of the
![]() $1\leq z \leq 4$
,
$1\leq z \leq 4$
,
![]() $10^{44}\leq \mathrm{L_x(erg\,s^{-1})}\leq 5 \times 10^{45}$
,
$10^{44}\leq \mathrm{L_x(erg\,s^{-1})}\leq 5 \times 10^{45}$
,
![]() $24\leq \log(\text{N}_{\text{H}}/\text{cm}^{-2})\leq 26$
bins and fitted them. If both the fitted luminosity and the column density, obtained from the spectral fitting, are within 30% of the input values, we say that we have ‘characterised’ the source. Finally, by dividing the number of characterised sources by 100 (the number of spectra we simulated), we have estimated the fraction of characterised sources in each bin.
$24\leq \log(\text{N}_{\text{H}}/\text{cm}^{-2})\leq 26$
bins and fitted them. If both the fitted luminosity and the column density, obtained from the spectral fitting, are within 30% of the input values, we say that we have ‘characterised’ the source. Finally, by dividing the number of characterised sources by 100 (the number of spectra we simulated), we have estimated the fraction of characterised sources in each bin.
5. AGN and host galaxy SED
To compute the AGN and host galaxy expected fluxes at different redshifts in the SPICA and OST bands, we need a proper set of SEDs to model the AGN as a function of different parameters: the intrinsic rest frame 2–10 keV luminosity
![]() $\text{L}_{\text{x}}$
, the equivalent hydrogen column density
$\text{L}_{\text{x}}$
, the equivalent hydrogen column density
![]() $\text{N}_{\text{H}}$
, and the redshift z.
$\text{N}_{\text{H}}$
, and the redshift z.
We started with the AGN and host galaxy SED compilation from Lanzuisi et al. (Reference Lanzuisi2017). They used a sample of
![]() $2\,333$
X-ray selected (either XMM-Newton or Chandra) AGN in the COSMOS field (Scoville et al. Reference Scoville2007) with at least 30 X-ray counts from Lanzuisi et al. (Reference Lanzuisi2013, Reference Lanzuisi2015), Marchesi et al. (Reference Marchesi2016) and then selected only those with a
$2\,333$
X-ray selected (either XMM-Newton or Chandra) AGN in the COSMOS field (Scoville et al. Reference Scoville2007) with at least 30 X-ray counts from Lanzuisi et al. (Reference Lanzuisi2013, Reference Lanzuisi2015), Marchesi et al. (Reference Marchesi2016) and then selected only those with a
![]() ${>}3\sigma$
IR detection in one of the Herschel bands. The X-ray spectral analysis provided us with column density
${>}3\sigma$
IR detection in one of the Herschel bands. The X-ray spectral analysis provided us with column density
![]() $\text{N}_{\text{H}}$
and absorption-corrected 2–
$\text{N}_{\text{H}}$
and absorption-corrected 2–
![]() $10\,$
keV luminosity for each source (see Lanzuisi et al. Reference Lanzuisi2017 and references therein for more details). The final sample was composed of 692 sources X-ray and Far InfraRed (FIR) detected, all with both X-ray spectral properties and SED decomposition. The SEDs were obtained by Delvecchio et al. (Reference Delvecchio2014, Reference Delvecchio2015), following the recipes described in Berta et al. (Reference Berta2013), using the sed3fit code (with a ‘smooth’ torus model), which allowed us to disentangle the AGN and host galaxy contribution using three components—stellar emission, AGN torus emission, and SF-heated dust emission—with photometric points from the UV to sub-mm. We excluded from our sample the sources with 2–10 keV rest frame luminosities
$10\,$
keV luminosity for each source (see Lanzuisi et al. Reference Lanzuisi2017 and references therein for more details). The final sample was composed of 692 sources X-ray and Far InfraRed (FIR) detected, all with both X-ray spectral properties and SED decomposition. The SEDs were obtained by Delvecchio et al. (Reference Delvecchio2014, Reference Delvecchio2015), following the recipes described in Berta et al. (Reference Berta2013), using the sed3fit code (with a ‘smooth’ torus model), which allowed us to disentangle the AGN and host galaxy contribution using three components—stellar emission, AGN torus emission, and SF-heated dust emission—with photometric points from the UV to sub-mm. We excluded from our sample the sources with 2–10 keV rest frame luminosities
![]() $\log(\mathrm{L_x/erg\,s^{-1}})<42$
, as SF galaxies without AGN should not be able to exceed this threshold. Moreover, to overcome the degeneracy between the AGN and the SF contribution during the SED fitting, we selected only the SEDs with AGN significance
$\log(\mathrm{L_x/erg\,s^{-1}})<42$
, as SF galaxies without AGN should not be able to exceed this threshold. Moreover, to overcome the degeneracy between the AGN and the SF contribution during the SED fitting, we selected only the SEDs with AGN significance
![]() $S_{AGN}\ge99\%$
, evaluated through the F-test between the best-fit reduced
$S_{AGN}\ge99\%$
, evaluated through the F-test between the best-fit reduced
![]() $\chi^2$
with and without the AGN component (see Delvecchio et al. Reference Delvecchio2014). Thus, the final sample is composed of 422 AGN in the redshift range
$\chi^2$
with and without the AGN component (see Delvecchio et al. Reference Delvecchio2014). Thus, the final sample is composed of 422 AGN in the redshift range
![]() $0 < z \leq 4$
, 2–10 keV rest frame luminosities in the
$0 < z \leq 4$
, 2–10 keV rest frame luminosities in the
![]() $42\leq \log(\mathrm{L_x/erg\,s}^{-1}) \leq 45.5$
range, and host galaxy masses
$42\leq \log(\mathrm{L_x/erg\,s}^{-1}) \leq 45.5$
range, and host galaxy masses
![]() $7.9 \le \log{\text{M}/{\rm M}_{\odot}} \le 12.2 $
.
$7.9 \le \log{\text{M}/{\rm M}_{\odot}} \le 12.2 $
.
With the aim of obtaining template SEDs representative of AGN with different intrinsic rest frame 2–10 keV luminosity and obscuration, we created four
![]() $\text{L}_{\text{x}}$
bins and four
$\text{L}_{\text{x}}$
bins and four
![]() $\text{N}_{\text{H}}$
bins. The binning was chosen to maximise the number of sources in each bin, while maintaining a good sampling of the
$\text{N}_{\text{H}}$
bins. The binning was chosen to maximise the number of sources in each bin, while maintaining a good sampling of the
![]() $\text{L}_{\text{x}}$
and
$\text{L}_{\text{x}}$
and
![]() $\text{N}_{\text{H}}$
parameter space. The binning used and the number of SEDs in each bin are shown in Table 3. Two of the most extreme bins had no sources in them; for these bins, we chose to use SEDs randomly extracted from the two nearest bins (one with the same
$\text{N}_{\text{H}}$
parameter space. The binning used and the number of SEDs in each bin are shown in Table 3. Two of the most extreme bins had no sources in them; for these bins, we chose to use SEDs randomly extracted from the two nearest bins (one with the same
![]() $\text{L}_{\text{x}}$
and one with the same
$\text{L}_{\text{x}}$
and one with the same
![]() $\text{N}_{\text{H}}$
). The binning choice was also driven by the binning we adopted to obtain the number of expected AGN (see Section 3) and we used the same binning edges, although we merged some of the less populated bins.
$\text{N}_{\text{H}}$
). The binning choice was also driven by the binning we adopted to obtain the number of expected AGN (see Section 3) and we used the same binning edges, although we merged some of the less populated bins.
Table 3. Number of binned sources, using the compilation of Lanzuisi et al. (Reference Lanzuisi2017) as explained in Section 5, in each 2–10 keV rest frame luminosity
![]() $\text{L}_{\text{x}}$
and amount of obscuration
$\text{L}_{\text{x}}$
and amount of obscuration
![]() $\text{N}_{\text{H}}$
bin. The used
$\text{N}_{\text{H}}$
bin. The used
![]() $\text{N}_{\text{H}}$
bins are
$\text{N}_{\text{H}}$
bins are
![]() $20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 22$
;
$20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 22$
;
![]() $22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
,
$22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
,
![]() $23 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 24.18 $
, and
$23 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 24.18 $
, and
![]() $24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 26$
. We refer to the sources in the first two
$24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 26$
. We refer to the sources in the first two
![]() $\text{L}_{\text{x}}$
bins as low-luminosity ones and to those in the other two as high-luminosity ones. We consider the sources in the first
$\text{L}_{\text{x}}$
bins as low-luminosity ones and to those in the other two as high-luminosity ones. We consider the sources in the first
![]() $\text{N}_{\text{H}}$
bin as unobscured AGN, those in the second and third bins as obscured and those in the last
$\text{N}_{\text{H}}$
bin as unobscured AGN, those in the second and third bins as obscured and those in the last
![]() $\text{N}_{\text{H}}$
bin as CT-AGN. For the two low-luminosity CT bins, we had no SED available and we chose to use the SED of the nearest bins.
$\text{N}_{\text{H}}$
bin as CT-AGN. For the two low-luminosity CT bins, we had no SED available and we chose to use the SED of the nearest bins.

Throughout this paper, we assumed a bolometric correction of
![]() $k_{bol}=L_{\rm bol}/{\rm L}_{\text{x}}$
, Equation (1), from Lusso et al. (Reference Lusso2012):
$k_{bol}=L_{\rm bol}/{\rm L}_{\text{x}}$
, Equation (1), from Lusso et al. (Reference Lusso2012):
In this work, we will refer to the predicted AGN in the simulated redshift range
![]() $0<z<10$
with
$0<z<10$
with
![]() $20\leq \mathrm{log(N_{H}/cm^{-2})} < 26$
and
$20\leq \mathrm{log(N_{H}/cm^{-2})} < 26$
and
![]() $42\leq \mathrm{log(L_{x}/erg\ s^{-1})}<48.2(43 \leq \mathrm{log}(L_{bol}/\mathrm{erg}\ \mathrm{s}^{-1})<49.7)$
, thus covering the whole simulated parameter space, as all the AGN. The naming scheme used for referring to AGN with different properties (namely, N
$42\leq \mathrm{log(L_{x}/erg\ s^{-1})}<48.2(43 \leq \mathrm{log}(L_{bol}/\mathrm{erg}\ \mathrm{s}^{-1})<49.7)$
, thus covering the whole simulated parameter space, as all the AGN. The naming scheme used for referring to AGN with different properties (namely, N
![]() $_{\text{H}}$
and luminosity) is reported in Table 4.
$_{\text{H}}$
and luminosity) is reported in Table 4.
Table 4. Naming scheme used in this work for referring to AGN with different amounts of obscuration and X-ray luminosity. As reported in Section 5, we used the Lusso et al. (Reference Lusso2012) bolometric correction (Equation (1)) to compute
![]() ${L}_{\text{bol}}$
.
${L}_{\text{bol}}$
.

Table 5. Percentage of all the AGN, CT-AGN, CT-AGN at
![]() $z \le 4$
, and CT-AGN at
$z \le 4$
, and CT-AGN at
![]() $z \le 2$
photometrically detected with various configurations of instruments and surveys. SMI refers to SPICA SMI-CAM. OSS refers to the sources detected with the OST OSS in photometric mode (
$z \le 2$
photometrically detected with various configurations of instruments and surveys. SMI refers to SPICA SMI-CAM. OSS refers to the sources detected with the OST OSS in photometric mode (
![]() $R=4$
) in at least one of the bands, while the number within the parenthesis to those with detection in all the six OSS bands. SMI AGN and OSS AGN refer to the direct detection of AGN emission (thus the cases where the AGN is more luminous than the host galaxy in the considered band) for, respectively, the SPICA SMI-CAM and the OST OSS instruments. WFI refers to the source photometrically detected by Athena WFI, while SMI + WFI (OSS + WFI) refers to the sources with both SMI-CAM (OSS) detection and Athena photometric detection.
$R=4$
) in at least one of the bands, while the number within the parenthesis to those with detection in all the six OSS bands. SMI AGN and OSS AGN refer to the direct detection of AGN emission (thus the cases where the AGN is more luminous than the host galaxy in the considered band) for, respectively, the SPICA SMI-CAM and the OST OSS instruments. WFI refers to the source photometrically detected by Athena WFI, while SMI + WFI (OSS + WFI) refers to the sources with both SMI-CAM (OSS) detection and Athena photometric detection.

Table 6. Percentage of all the AGN, CT-AGN, CT-AGN at
![]() $z \le 4$
, and CT-AGN at
$z \le 4$
, and CT-AGN at
![]() $z \le 2$
spectroscopically detected with various configurations of instruments and surveys. SMIsp refers to SPICA SMI-LR. OSSsp refers to the sources detected with the OST OSS in spectroscopic mode (
$z \le 2$
spectroscopically detected with various configurations of instruments and surveys. SMIsp refers to SPICA SMI-LR. OSSsp refers to the sources detected with the OST OSS in spectroscopic mode (
![]() $R=300$
) in at least one of the bands, while the number within the parenthesis to those with detection in all the six OSS bands. WFIsp refers to the source spectroscopically detected by Athena WFI, while SMIsp + WFI (OSSsp + WFI) refers to the sources with both SMI-LR (OSS) spectroscopic detection and Athena photometric detection.
$R=300$
) in at least one of the bands, while the number within the parenthesis to those with detection in all the six OSS bands. WFIsp refers to the source spectroscopically detected by Athena WFI, while SMIsp + WFI (OSSsp + WFI) refers to the sources with both SMI-LR (OSS) spectroscopic detection and Athena photometric detection.

6. Predictions of IR source counts
In Section 3, we predicted the number of expected AGN (per
![]() $\mathrm{deg}^2$
) as function of z,
$\mathrm{deg}^2$
) as function of z,
![]() $\text{L}_{\text{x}}$
and
$\text{L}_{\text{x}}$
and
![]() $\text{N}_{\text{H}}$
. For each z,
$\text{N}_{\text{H}}$
. For each z,
![]() $\text{L}_{\text{x}}$
, and
$\text{L}_{\text{x}}$
, and
![]() $\text{N}_{\text{H}}$
, bin we randomly extracted 20 template SEDs, from the corresponding bins in Section 5 and assigned them a weight equal to one-twentieth of the total number of predicted AGN. We measured their total (AGN + host) flux densities in the SMI
$\text{N}_{\text{H}}$
, bin we randomly extracted 20 template SEDs, from the corresponding bins in Section 5 and assigned them a weight equal to one-twentieth of the total number of predicted AGN. We measured their total (AGN + host) flux densities in the SMI
![]() $34\,\unicode[Times]{x03BC}$
m and B-BOP 70, 200, and
$34\,\unicode[Times]{x03BC}$
m and B-BOP 70, 200, and
![]() $350\unicode[Times]{x03BC}$
m bands (for SPICA) and in the six OSS bands (for OST). We obtained the number sources detectable at
$350\unicode[Times]{x03BC}$
m bands (for SPICA) and in the six OSS bands (for OST). We obtained the number sources detectable at
![]() $5\,\sigma$
by summing the weights of the sources with flux larger than the survey sensitivity.
$5\,\sigma$
by summing the weights of the sources with flux larger than the survey sensitivity.
In case of detection, we also differentiated if we were primarily detecting either the AGN or the host galaxy, on the basis of which of the two components had the highest flux in the band we were considering. In the case of a SPICA SMI
![]() $34\,\unicode[Times]{x03BC}$
m detection, we considered whether we could also detect the source with the SMI-LR mode (as the SMI-CAM photometric channel operates at the same time with the SMI-LR spectroscopic channel). We used, as SMI-LR sensitivity, a mean value between the sensitivities at the boundaries of the SMI-LR wavelength range. For OST OSS, we always considered both the detection in photometric mode (
$34\,\unicode[Times]{x03BC}$
m detection, we considered whether we could also detect the source with the SMI-LR mode (as the SMI-CAM photometric channel operates at the same time with the SMI-LR spectroscopic channel). We used, as SMI-LR sensitivity, a mean value between the sensitivities at the boundaries of the SMI-LR wavelength range. For OST OSS, we always considered both the detection in photometric mode (
![]() $R=4$
) and in spectroscopic mode (
$R=4$
) and in spectroscopic mode (
![]() $R=300$
).
$R=300$
).
We iterated this whole process 40 times (different SEDs were extracted at each iteration), each time obtaining an estimate for the number of detected sources, AGN/torus, and spectroscopic detection. We computed the median of these numbers and used the 16–84
![]() ${\text{th}}$
percentiles as uncertainties. Extracting 20 SEDs for each bin (and not one SED for each of the expected detection in that bin) allowed us to save computational time while maintaining a result resolution of 5%. We chose to iterate the process 40 times to have good statistical significance of the median and of the
${\text{th}}$
percentiles as uncertainties. Extracting 20 SEDs for each bin (and not one SED for each of the expected detection in that bin) allowed us to save computational time while maintaining a result resolution of 5%. We chose to iterate the process 40 times to have good statistical significance of the median and of the
![]() $16-84^{\text{th}}$
percentiles.
$16-84^{\text{th}}$
percentiles.
In conclusion, from the IR simulations, we derive, for each bin, the percentage of sources photometrically detected, spectroscopically detected, and for which it is the AGN emission to be primarily detected. From the X-ray simulations, we obtained the total number of AGN in each bin, as well as the fraction of sources photometrically detected and spectroscopically characterised using Athena WFI. In each bin, we computed the fraction of sources detected both in the IR and in the X-rays, as the minimum between the detection fraction in the two wavelength ranges. Although, in some bins, there may be sources detected in the IR and not in the X-rays, alongside those detected in the X-rays and not in the IR, usually the detection fraction in one of the wavelength ranges is much higher than the other, and we can safely consider the minimum as a reliably estimate of the fraction of sources detectable with both instruments.
We summarise the main results of our prediction in Tables 5 and 6. Figures 1, 2, 3, and 4 illustrate the number of photometric detections per
![]() $\mathrm{deg}^2$
for SPICA-SMI DEEP, SPICA-SMI WIDE, OSS DEEP, and OSS WIDE, respectively. All the figures also report the number of sources detected by Athena WFI. The black lines are the total number of AGN expected, the red areas represent those which can be detected using SPICA SMI-CAM at 34
$\mathrm{deg}^2$
for SPICA-SMI DEEP, SPICA-SMI WIDE, OSS DEEP, and OSS WIDE, respectively. All the figures also report the number of sources detected by Athena WFI. The black lines are the total number of AGN expected, the red areas represent those which can be detected using SPICA SMI-CAM at 34
![]() $\unicode[Times]{x03BC}$
m (or band 1 of OSS), the blue areas those which can be detected in the X-rays by Athena, and the purple areas are the AGN that can be detected both by SPICA SMI-CAM (or OSS) and by Athena. The red uniform area represents the IR detected sources in which the main component of emission is due to the host galaxy, while for those represented with the starry red area, the AGN is the main contributor to the detected emission. Figures 5 and 6 have a similar color code, but with the dashed areas representing the sources for which we will have spectrocopic detection in a DEEP survey with a SPICA SMI-LR-like instrument or with the OSS. Finally, Figure 7 (Figure 8) shows a comparison of the number of sources that we will be able to detect in a DEEP (WIDE) survey with SPICA and OST, with the color code indicating the expected number of photometric bands in which we may detect the source (considering SMI-CAM and B-BOP for SPICA and the six OSS bands for the OST).
$\unicode[Times]{x03BC}$
m (or band 1 of OSS), the blue areas those which can be detected in the X-rays by Athena, and the purple areas are the AGN that can be detected both by SPICA SMI-CAM (or OSS) and by Athena. The red uniform area represents the IR detected sources in which the main component of emission is due to the host galaxy, while for those represented with the starry red area, the AGN is the main contributor to the detected emission. Figures 5 and 6 have a similar color code, but with the dashed areas representing the sources for which we will have spectrocopic detection in a DEEP survey with a SPICA SMI-LR-like instrument or with the OSS. Finally, Figure 7 (Figure 8) shows a comparison of the number of sources that we will be able to detect in a DEEP (WIDE) survey with SPICA and OST, with the color code indicating the expected number of photometric bands in which we may detect the source (considering SMI-CAM and B-BOP for SPICA and the six OSS bands for the OST).

Figure 1. Number of AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
for a SPICA-like DEEP survey. The black lines are the total number of expected AGN, the red areas represent those which can be detected with the SPICA SMI-CAM at 34
$\Delta z =1$
for a SPICA-like DEEP survey. The black lines are the total number of expected AGN, the red areas represent those which can be detected with the SPICA SMI-CAM at 34
![]() $\unicode[Times]{x03BC}$
m, the blue areas those which can be detected in the X-rays with the Athena WFI, and the purple areas are the AGN that will be detected both by SPICA SMI-CAM and Athena. The red uniform area represents the sources detected by SPICA in which the main component is due to the host galaxy emission, while for those represented with the starry red area the AGN is the main contributor to the detected emission. The columns refer to AGN with different amount of obscuration (
$\unicode[Times]{x03BC}$
m, the blue areas those which can be detected in the X-rays with the Athena WFI, and the purple areas are the AGN that will be detected both by SPICA SMI-CAM and Athena. The red uniform area represents the sources detected by SPICA in which the main component is due to the host galaxy emission, while for those represented with the starry red area the AGN is the main contributor to the detected emission. The columns refer to AGN with different amount of obscuration (
![]() $20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 21$
;
$20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 21$
;
![]() $22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
;
$22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
;
![]() $24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 25$
, from left to right), the rows to different AGN luminosity (
$24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 25$
, from left to right), the rows to different AGN luminosity (
![]() $42.0\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <42.3 $
,
$42.0\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <42.3 $
,
![]() $42.9\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <43.2 $
,
$42.9\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <43.2 $
,
![]() $43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <44.2 $
,
$43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <44.2 $
,
![]() $44.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <45.2 $
, from top to bottom). For 40 times we extracted 20 SEDs for each bin, we measured the flux in each SPICA band and compared them with the
$44.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <45.2 $
, from top to bottom). For 40 times we extracted 20 SEDs for each bin, we measured the flux in each SPICA band and compared them with the
![]() $5\,\sigma$
sensitivities to compute the number of detectable sources. The median of these 40 values are the numbers used in this figure, while the 84–16th percentiles are used as uncertainties (not reported in the figure).
$5\,\sigma$
sensitivities to compute the number of detectable sources. The median of these 40 values are the numbers used in this figure, while the 84–16th percentiles are used as uncertainties (not reported in the figure).

Figure 2. Number of AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
for a SPICA-like DEEP survey. The lines and areas are coded as in Figure 1.
$\Delta z =1$
for a SPICA-like DEEP survey. The lines and areas are coded as in Figure 1.

Figure 3. Number of AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
for a OST OSS DEEP survey. The black lines are the total number of expected AGN, the red areas represent those which can be detected in the band 1 by OST OSS, the blue areas those which can be detected in the X-rays with the Athena WFI, and the purple areas are the AGN that will be detected both by OSS and Athena. The red uniform area represents the sources detected by OSS in which the main component is due to the host galaxy emission, while for those represented with the starry red area the AGN is the main contributor to the detected emission. The columns refer to AGN with different amount of obscuration (
$\Delta z =1$
for a OST OSS DEEP survey. The black lines are the total number of expected AGN, the red areas represent those which can be detected in the band 1 by OST OSS, the blue areas those which can be detected in the X-rays with the Athena WFI, and the purple areas are the AGN that will be detected both by OSS and Athena. The red uniform area represents the sources detected by OSS in which the main component is due to the host galaxy emission, while for those represented with the starry red area the AGN is the main contributor to the detected emission. The columns refer to AGN with different amount of obscuration (
![]() $20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 21$
;
$20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 21$
;
![]() $22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
;
$22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
;
![]() $24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 25$
, from left to right), the rows to different AGN luminosity (
$24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 25$
, from left to right), the rows to different AGN luminosity (
![]() $42.0\le \log{(\text{L}_{\text{x}}/\text{erg} \, \text{s}^{-1})} <42.3 $
,
$42.0\le \log{(\text{L}_{\text{x}}/\text{erg} \, \text{s}^{-1})} <42.3 $
,
![]() $42.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <43.2 $
,
$42.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <43.2 $
,
![]() $43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <44.2 $
,
$43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <44.2 $
,
![]() $44.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <45.2 $
, from top to bottom). For 40 times we extracted 20 SEDs for each bin, we measured the flux in each OST band and compared them with the
$44.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <45.2 $
, from top to bottom). For 40 times we extracted 20 SEDs for each bin, we measured the flux in each OST band and compared them with the
![]() $5\,\sigma$
sensitivities to compute the number of detectable sources. The median of these 40 values are the numbers used in this figure, while the 84–16th percentiles are used as uncertainties (not reported in the figure).
$5\,\sigma$
sensitivities to compute the number of detectable sources. The median of these 40 values are the numbers used in this figure, while the 84–16th percentiles are used as uncertainties (not reported in the figure).

Figure 4. Number of AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
for a OST OSS WIDE survey. The lines and areas are coded as in Figure 3.
$\Delta z =1$
for a OST OSS WIDE survey. The lines and areas are coded as in Figure 3.

Figure 5. Number of AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
for a SPICA-like DEEP survey. The black lines are the total number of AGN expected, the red areas represent those which can be detected with the SPICA SMI-CAM at 34
$\Delta z =1$
for a SPICA-like DEEP survey. The black lines are the total number of AGN expected, the red areas represent those which can be detected with the SPICA SMI-CAM at 34
![]() $\unicode[Times]{x03BC}$
m, the blue areas those which can be detected in the X-rays by Athena SMI, and the purple areas are the AGN that will be detected both by SPICA SMI-CAM and Athena. The dashed areas represent the sources which could be spectroscopically detected with SMI-LR (
$\unicode[Times]{x03BC}$
m, the blue areas those which can be detected in the X-rays by Athena SMI, and the purple areas are the AGN that will be detected both by SPICA SMI-CAM and Athena. The dashed areas represent the sources which could be spectroscopically detected with SMI-LR (
![]() $5\,\sigma$
detection with a resolution
$5\,\sigma$
detection with a resolution
![]() $R=50$
–120 in the 17–
$R=50$
–120 in the 17–
![]() $36\,\unicode[Times]{x03BC}$
m wavelength range). The columns refer to AGN with different amount of obscuration (
$36\,\unicode[Times]{x03BC}$
m wavelength range). The columns refer to AGN with different amount of obscuration (
![]() $20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 21$
;
$20 \le \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 21$
;
![]() $22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
;
$22 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 23$
;
![]() $24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 25$
, from left to right), the rows to different AGN luminosity (
$24.18 < \log\, (\text{N}_{\text{H}}/\text{cm}^{-2}) \le 25$
, from left to right), the rows to different AGN luminosity (
![]() $42.0\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <42.5 $
,
$42.0\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <42.5 $
,
![]() $42.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <43.2 $
,
$42.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <43.2 $
,
![]() $43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <44.2 $
,
$43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <44.2 $
,
![]() $44.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <45.2 $
, from top to bottom).
$44.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <45.2 $
, from top to bottom).
6.1. Photometric detections
Considering the DEEP survey we will be able to detect in the IR
![]() ${\gtrsim}90\%$
of all the AGN, approximately half of them will have photometric detection both in the IR and in the X-ray bands; this synergy will allow us to identify the source as an AGN and will help in placing better constraints to its properties. By a DEEP survey, working jointly, a IR cryogenic observatory (like SPICA or OST) and Athena can detect all the AGN up to
${\gtrsim}90\%$
of all the AGN, approximately half of them will have photometric detection both in the IR and in the X-ray bands; this synergy will allow us to identify the source as an AGN and will help in placing better constraints to its properties. By a DEEP survey, working jointly, a IR cryogenic observatory (like SPICA or OST) and Athena can detect all the AGN up to
![]() $z=4$
, de facto completely covering the ‘cosmic noon’ and bringing important insights about the AGN density evolution at higher redshifts. At the same time, the bulk of the intrinsic X-ray emission is produced at the ‘knee’ of the luminosity function (
$z=4$
, de facto completely covering the ‘cosmic noon’ and bringing important insights about the AGN density evolution at higher redshifts. At the same time, the bulk of the intrinsic X-ray emission is produced at the ‘knee’ of the luminosity function (
![]() $\text{L}_{\text{x}}\sim 5 \times 10^{44}\,\mathrm{erg\ s}^{-1}$
for
$\text{L}_{\text{x}}\sim 5 \times 10^{44}\,\mathrm{erg\ s}^{-1}$
for
![]() $z \sim 1{-}4$
, Aird et al. Reference Aird2010) and these sources will be easily detected and characterised by Athena up to
$z \sim 1{-}4$
, Aird et al. Reference Aird2010) and these sources will be easily detected and characterised by Athena up to
![]() $z \sim 3$
. Moreover, Athena will be of paramount importance to identify as AGN even sources for which the IR torus emission is diluted and hidden behind the more powerful host galaxy contribution. The combined used of data in both bands will be fundamental in obtaining a more robust estimate of the AGN bolometric power. In particular, on the one hand, obtaining the AGN bolometric power with only X-ray data requires to assume an AGN X-ray bolometric correction, thus introducing large uncertainties in the derived values, due to our limited knowledge of the
$z \sim 3$
. Moreover, Athena will be of paramount importance to identify as AGN even sources for which the IR torus emission is diluted and hidden behind the more powerful host galaxy contribution. The combined used of data in both bands will be fundamental in obtaining a more robust estimate of the AGN bolometric power. In particular, on the one hand, obtaining the AGN bolometric power with only X-ray data requires to assume an AGN X-ray bolometric correction, thus introducing large uncertainties in the derived values, due to our limited knowledge of the
![]() $k_{\rm bol}-{L}_{\rm bol}$
relation (Hopkins et al. Reference Hopkins, Richards and Hernquist2007; Lusso et al. Reference Lusso2010, Reference Lusso2012; Duras et al. Reference Duras2020). On the other hand, using only an instrument similar to SPICA SMI-CAM, it will not be possible to distinguish between the AGN and the galaxy emission, as SPICA SMI-CAM can measure only the total (AGN + host galaxy) emission.
$k_{\rm bol}-{L}_{\rm bol}$
relation (Hopkins et al. Reference Hopkins, Richards and Hernquist2007; Lusso et al. Reference Lusso2010, Reference Lusso2012; Duras et al. Reference Duras2020). On the other hand, using only an instrument similar to SPICA SMI-CAM, it will not be possible to distinguish between the AGN and the galaxy emission, as SPICA SMI-CAM can measure only the total (AGN + host galaxy) emission.

Figure 6. Number of AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
for a OSS DEEP survey. The lines and areas are coded as in Figure 5, but with the red areas referring to the band 1 of the OST OSS instrument.
$\Delta z =1$
for a OSS DEEP survey. The lines and areas are coded as in Figure 5, but with the red areas referring to the band 1 of the OST OSS instrument.

Figure 7. Distribution of the number of AGN expected per
![]() $\mathrm{deg}^2$
for a SPICA-like (top panel) and for the OST OSS (bottom panel) from a DEEP survey. The color code indicates our predictions for the number of photometric detections. For the SPICA panel, we took into consideration the SMI-CAM and the three B-BOP channel, while the dashed area represents the sources which can be spectroscopically detected with a SMI-LR-like instrument (
$\mathrm{deg}^2$
for a SPICA-like (top panel) and for the OST OSS (bottom panel) from a DEEP survey. The color code indicates our predictions for the number of photometric detections. For the SPICA panel, we took into consideration the SMI-CAM and the three B-BOP channel, while the dashed area represents the sources which can be spectroscopically detected with a SMI-LR-like instrument (
![]() $5\,\sigma$
detection with a resolution
$5\,\sigma$
detection with a resolution
![]() $R=50$
–120 in the 17–
$R=50$
–120 in the 17–
![]() $36\,\unicode[Times]{x03BC}$
m wavelength range). For the OST panel, we consider the six OSS bands in photometric mode (
$36\,\unicode[Times]{x03BC}$
m wavelength range). For the OST panel, we consider the six OSS bands in photometric mode (
![]() $R=4$
), while the dashed line indicates the sources for which we can have
$R=4$
), while the dashed line indicates the sources for which we can have
![]() $R=300$
spectra in at least one of the OSS bands.
$R=300$
spectra in at least one of the OSS bands.

Figure 8. Distribution of the number of AGN expected per
![]() $\mathrm{deg}^2$
for a SPICA-like (top panel) and for the OST OSS (bottom panel) from a WIDE survey. The lines and areas are coded as in Figure 7.
$\mathrm{deg}^2$
for a SPICA-like (top panel) and for the OST OSS (bottom panel) from a WIDE survey. The lines and areas are coded as in Figure 7.
Considering a WIDE survey, the fractions of sources that will be detected are lower of
![]() ${\sim}20\,\%$
with respect to the DEEP survey, but the (at least) 15 times wider area will allow us to detect at least 10 times more sources. Similarly to the DEEP, the WIDE survey may allow us to perfectly cover the ‘cosmic noon’ with the advantage of a ten-folded statistic (at least). In a WIDE survey, Athena WFI may loose a significant fraction of the most obscured AGN or of the low-luminosity ones. However, a SPICA-like (or OST-like) mission should be able to effectively recover these sources, although we may need an effective way (e.g. SPICA-SAFARI or OST spectroscopic follow-up, see Sections 6.2 and 6.3) to characterise their AGN properties (intrinsic bolometric luminosity and amount of obscuration). For this shallower survey, it is still valid our statement that, for most of the detected sources at
${\sim}20\,\%$
with respect to the DEEP survey, but the (at least) 15 times wider area will allow us to detect at least 10 times more sources. Similarly to the DEEP, the WIDE survey may allow us to perfectly cover the ‘cosmic noon’ with the advantage of a ten-folded statistic (at least). In a WIDE survey, Athena WFI may loose a significant fraction of the most obscured AGN or of the low-luminosity ones. However, a SPICA-like (or OST-like) mission should be able to effectively recover these sources, although we may need an effective way (e.g. SPICA-SAFARI or OST spectroscopic follow-up, see Sections 6.2 and 6.3) to characterise their AGN properties (intrinsic bolometric luminosity and amount of obscuration). For this shallower survey, it is still valid our statement that, for most of the detected sources at
![]() $\log(\mathrm{N_H/cm}^{-2})\leq23$
,
$\log(\mathrm{N_H/cm}^{-2})\leq23$
,
![]() $\log(\mathrm{L_x/erg\ s}^{-1})> 43$
and
$\log(\mathrm{L_x/erg\ s}^{-1})> 43$
and
![]() $z \le 3$
(and higher z for higher L
$z \le 3$
(and higher z for higher L
![]() $_{\text{x}}$
), Athena detections would provide essential evidence of the AGN nature of those sources.
$_{\text{x}}$
), Athena detections would provide essential evidence of the AGN nature of those sources.
Focusing on OST, the six spectrophometric bands of OSS will give us a good coverage at and beyond the ‘cosmic noon’ even in photometric mode. Moreover, thanks to the capabilities of OSS, for the majority of the sources detected by Athena, we will have six photometric points (and maybe up to six spectra) in the mid- and far-IR.
6.2. Spectroscopic detections
We estimated that, exploiting Athena WFI spectra, we will be able to recover the intrinsic AGN luminosity and obscuration (with
![]() $30\,\%$
uncertainties) for
$30\,\%$
uncertainties) for
![]() ${\approx}20\,\%$
of all the AGN and up to
${\approx}20\,\%$
of all the AGN and up to
![]() ${\approx}50\,\%$
of the high-luminosity ones. Even low-count X-ray spectra will allow reliable
${\approx}50\,\%$
of the high-luminosity ones. Even low-count X-ray spectra will allow reliable
![]() $\text{N}_{\text{H}}$
characterisation, as for obscured and CT-AGN, we expect simple spectra with a flat continuum and a possibly strong iron K
$\text{N}_{\text{H}}$
characterisation, as for obscured and CT-AGN, we expect simple spectra with a flat continuum and a possibly strong iron K
![]() $\alpha$
line. Furthermore, an X-ray detection at a level of
$\alpha$
line. Furthermore, an X-ray detection at a level of
![]() $\sim\!2\times 10^{-16}\ \mathrm{erg\ cm}^{-2} \mathrm{s}^{-1}$
in the
$\sim\!2\times 10^{-16}\ \mathrm{erg\ cm}^{-2} \mathrm{s}^{-1}$
in the
![]() $2{-}10$
keV band at
$2{-}10$
keV band at
![]() $z \ge 1$
, or simply any detection at
$z \ge 1$
, or simply any detection at
![]() $z \gtrsim 2.3$
in the DEEP survey, imply X-ray luminosities
$z \gtrsim 2.3$
in the DEEP survey, imply X-ray luminosities
![]() ${\gtrsim}10^{42}\,\mathrm{erg}\, \text{s}^{-1}$
in that band, revealing almost unequivocally an AGN.
${\gtrsim}10^{42}\,\mathrm{erg}\, \text{s}^{-1}$
in that band, revealing almost unequivocally an AGN.
Considering a SMI-LR-like instrument (Figure 5), we find that with a DEEP survey we will be able to detect spectroscopically more than half of all the AGN within
![]() $z=2$
. For the high-luminosity objects, we expect to have some spectroscopic detections even up to
$z=2$
. For the high-luminosity objects, we expect to have some spectroscopic detections even up to
![]() $z\approx 4$
. Considering a WIDE survey, the fraction of AGN that we should be able to detect spectroscopically drops considerably. For the sources for which a fast low-resolution spectroscopic characterisation will not be possible, we may make use of photometric data (such as those produced by SMI-CAM-, or B-BOP-like instruments) and of SED-fitting technique (see Section 6.3) to disentangle the AGN and SF emissions.
$z\approx 4$
. Considering a WIDE survey, the fraction of AGN that we should be able to detect spectroscopically drops considerably. For the sources for which a fast low-resolution spectroscopic characterisation will not be possible, we may make use of photometric data (such as those produced by SMI-CAM-, or B-BOP-like instruments) and of SED-fitting technique (see Section 6.3) to disentangle the AGN and SF emissions.
Considering the OSS, we find that, with a DEEP survey, we will be able to detect spectroscopically between
![]() $55 \pm 6\%$
and
$55 \pm 6\%$
and
![]() $81 \pm 3\%$
of all the AGN, depending on the OSS band considered. Thus, we will have
$81 \pm 3\%$
of all the AGN, depending on the OSS band considered. Thus, we will have
![]() $R=300$
full IR spectra for more than half of all the predicted AGN at
$R=300$
full IR spectra for more than half of all the predicted AGN at
![]() $z\le 10$
. For the high-luminosity objects, we expect to have some spectroscopic detections even up to
$z\le 10$
. For the high-luminosity objects, we expect to have some spectroscopic detections even up to
![]() $z > 4$
. In the WIDE survey, the fraction of AGN that we should be able to detect spectroscopically lowers of
$z > 4$
. In the WIDE survey, the fraction of AGN that we should be able to detect spectroscopically lowers of
![]() ${\approx}30\,\%$
with respect to the DEEP survey.
${\approx}30\,\%$
with respect to the DEEP survey.
Several important galaxy and AGN mid-IR spectral features fall in the wavelength range of a SPICA SMI-LR-like (or OSS) instrument and can be of fundamental importance in both characterising AGN and host galaxy properties and measuring the redshift. In particular, we expect AGN-related high-ionisation lines,Footnote j such as [Ne v]14.3 and
![]() $24.3\,\unicode[Times]{x03BC}$
m, [O iv]
$24.3\,\unicode[Times]{x03BC}$
m, [O iv]
![]() $25.9\,\unicode[Times]{x03BC}$
m (e.g. Tommasin et al. Reference Tommasin2008, Reference Tommasin, Spinoglio, Malkan and Fazio2010; Feltre, Charlot, & Gutkin Reference Feltre, Charlot and Gutkin2016), but also SF-related polycyclic aromatic hydrocarbons (PAHs) features (e.g. Leger, D’Hendecourt, & Defourneau Reference Leger, D’Hendecourt and Defourneau1989) and the
$25.9\,\unicode[Times]{x03BC}$
m (e.g. Tommasin et al. Reference Tommasin2008, Reference Tommasin, Spinoglio, Malkan and Fazio2010; Feltre, Charlot, & Gutkin Reference Feltre, Charlot and Gutkin2016), but also SF-related polycyclic aromatic hydrocarbons (PAHs) features (e.g. Leger, D’Hendecourt, & Defourneau Reference Leger, D’Hendecourt and Defourneau1989) and the
![]() $9.7$
and
$9.7$
and
![]() $18\,\unicode[Times]{x03BC}$
m silicate features. The
$18\,\unicode[Times]{x03BC}$
m silicate features. The
![]() $9.7\unicode[Times]{x03BC}$
m feature is typically associated with type 1 AGN when observed in emission and with type 2 when it is in absorption (with the few notable exceptions of the type 2 quasars of Sturm et al. Reference Sturm2006; Teplitz et al. Reference Teplitz2006, which show the silicate feature in emission); moreover, more obscured AGN usually have deeper silicate features, with depths that correlate with the X-ray derived
$9.7\unicode[Times]{x03BC}$
m feature is typically associated with type 1 AGN when observed in emission and with type 2 when it is in absorption (with the few notable exceptions of the type 2 quasars of Sturm et al. Reference Sturm2006; Teplitz et al. Reference Teplitz2006, which show the silicate feature in emission); moreover, more obscured AGN usually have deeper silicate features, with depths that correlate with the X-ray derived
![]() $\text{N}_{\text{H}}$
(e.g. Wu et al. Reference Wu, Charmandaris, Huang, Spinoglio and Tommasin2009; Shi et al. Reference Shi2006, but see also Goulding et al. Reference Goulding2012).
$\text{N}_{\text{H}}$
(e.g. Wu et al. Reference Wu, Charmandaris, Huang, Spinoglio and Tommasin2009; Shi et al. Reference Shi2006, but see also Goulding et al. Reference Goulding2012).
Considering the AGN spectroscopic properties, the most evident mid-IR AGN lines ([Ne v]
![]() $14.3$
and
$14.3$
and
![]() $24.3\,\unicode[Times]{x03BC}$
m, [O iv]
$24.3\,\unicode[Times]{x03BC}$
m, [O iv]
![]() $25.9\,\unicode[Times]{x03BC}$
m) are redshifted out of a SMI-LR spectral range at modest redshift (
$25.9\,\unicode[Times]{x03BC}$
m) are redshifted out of a SMI-LR spectral range at modest redshift (
![]() $z < 1$
) and would require follow-ups with either SPICA-SAFARI or SMI-MR to be properly detected. In particular, exploting 5-h pointed observations with a SPICA SAFARI-like instruments, for low-luminosity (high-luminosity) unobscured AGN the [Ne v]
$z < 1$
) and would require follow-ups with either SPICA-SAFARI or SMI-MR to be properly detected. In particular, exploting 5-h pointed observations with a SPICA SAFARI-like instruments, for low-luminosity (high-luminosity) unobscured AGN the [Ne v]
![]() $24.3\,\unicode[Times]{x03BC}$
m and [O iv]
$24.3\,\unicode[Times]{x03BC}$
m and [O iv]
![]() $25.9\,\unicode[Times]{x03BC}$
m lines can be studied up to
$25.9\,\unicode[Times]{x03BC}$
m lines can be studied up to
![]() $z \approx 1$
and
$z \approx 1$
and
![]() $z \approx 2$
(
$z \approx 2$
(
![]() $z \approx 3$
and
$z \approx 3$
and
![]() $z \approx 4$
). The same lines can be detected up to
$z \approx 4$
). The same lines can be detected up to
![]() $z \approx 1.5$
and
$z \approx 1.5$
and
![]() $z \approx 2.5$
(
$z \approx 2.5$
(
![]() $z \approx 4$
and
$z \approx 4$
and
![]() $z \geq 4$
) for low-luminosity (high-luminosity) obscured AGN (Spinoglio et al. Reference Spinoglio2017, Reference Spinoglio2021). For the majority of the sources, the brightest and most recognisable features may be due to the galaxy emission, in particular the dust continuum and the PAH emission lines (e.g. Lutz et al. Reference Lutz, Spoon, Rigopoulou, Moorwood and Genzel1998; Hollenbach & Tielens Reference Hollenbach and Tielens1999; Yan et al. Reference Yan2007; Fadda et al. Reference Fadda2010; Spinoglio et al. Reference Spinoglio2021). However, for most cases, we expect the
$z \geq 4$
) for low-luminosity (high-luminosity) obscured AGN (Spinoglio et al. Reference Spinoglio2017, Reference Spinoglio2021). For the majority of the sources, the brightest and most recognisable features may be due to the galaxy emission, in particular the dust continuum and the PAH emission lines (e.g. Lutz et al. Reference Lutz, Spoon, Rigopoulou, Moorwood and Genzel1998; Hollenbach & Tielens Reference Hollenbach and Tielens1999; Yan et al. Reference Yan2007; Fadda et al. Reference Fadda2010; Spinoglio et al. Reference Spinoglio2021). However, for most cases, we expect the
![]() $9.7\,\unicode[Times]{x03BC}$
m silicate feature, to be easily recognisable. The silicate feature can be helpful in estimating the AGN amount of obscuration (e.g. Vignali et al. Reference Vignali2011; La Caria et al. Reference La Caria, Vignali, Lanzuisi, Gruppioni and Pozzi2019) and can be entirely within a SMI-LR-like instrument wavelength range up to
$9.7\,\unicode[Times]{x03BC}$
m silicate feature, to be easily recognisable. The silicate feature can be helpful in estimating the AGN amount of obscuration (e.g. Vignali et al. Reference Vignali2011; La Caria et al. Reference La Caria, Vignali, Lanzuisi, Gruppioni and Pozzi2019) and can be entirely within a SMI-LR-like instrument wavelength range up to
![]() $z \approx 3$
. This is particularly important for the CT-AGN, for which, with the exception of the most luminous ones (
$z \approx 3$
. This is particularly important for the CT-AGN, for which, with the exception of the most luminous ones (
![]() $\text{L}_{\text{x}} \approx 10^{44}$
erg/s for
$\text{L}_{\text{x}} \approx 10^{44}$
erg/s for
![]() $z<3$
), it will be difficult to obtain the AGN properties using only X-ray spectroscopy. Thus, the analysis of both X-ray and IR spectroscopic data will play a fundamental role in discerning their characteristics.
$z<3$
), it will be difficult to obtain the AGN properties using only X-ray spectroscopy. Thus, the analysis of both X-ray and IR spectroscopic data will play a fundamental role in discerning their characteristics.
One of the advantages of using a SPICA SMI-like (or OSS-like) instrument is that it can provide, at the same time, photometry and spectroscopy, and it can quickly produce low-resolution spectroscopic data for a large number of sources. X-ray spectral analysis is, so far, the best way to characterise the AGN (e.g. to determine the intrinsic luminosity), but it requires a redshift determination. Fortunately, there is a good prospect that redshifts can be determined solely from X-ray spectra (e.g. Simmonds et al. Reference Simmonds, Buchner, Salvato, Hsu and Bauer2018; Peca et al. Reference Peca2021). We simulated mid-IR spectra to evaluate the possibility of measuring the redshift from a SMI-LR-like spectra. In particular, we used a code that exploits the most prominent PAH features to recover the redshift. This implies that it is most suited for sources with sufficient SF to produce strong PAH features and low- or moderate-luminosity AGN, as the equivalent width of the PAH features is greatly reduced when the AGN luminosity is high (Voit Reference Voit1992; Genzel et al. Reference Genzel1998; O’Dowd et al. Reference O’Dowd2009). We chose 10 sources among the
![]() $\sim\!500$
of our sample and use their SEDs as spectral templates. The 10 sources were chosen so that in our sample there were un-obscured, obscured, and CT-AGN, high- and low- luminosity sources, AGN- and host-dominated sources, with emission and absorption
$\sim\!500$
of our sample and use their SEDs as spectral templates. The 10 sources were chosen so that in our sample there were un-obscured, obscured, and CT-AGN, high- and low- luminosity sources, AGN- and host-dominated sources, with emission and absorption
![]() $9.7\,\unicode[Times]{x03BC}$
m features. For each template, we simulated 16 spectra in the redshift range
$9.7\,\unicode[Times]{x03BC}$
m features. For each template, we simulated 16 spectra in the redshift range
![]() $0.5 \le z \le 6$
(as we can see from Figure 5, at
$0.5 \le z \le 6$
(as we can see from Figure 5, at
![]() $z>6$
the fraction of spectroscopically detected sources is very small). The simulated spectra were created accordingly to the latest SMI specifications. We used a spectral resolution of
$z>6$
the fraction of spectroscopically detected sources is very small). The simulated spectra were created accordingly to the latest SMI specifications. We used a spectral resolution of
![]() $R=50$
at
$R=50$
at
![]() $17\,\unicode[Times]{x03BC}$
m and
$17\,\unicode[Times]{x03BC}$
m and
![]() $R=120$
at
$R=120$
at
![]() $36\,\unicode[Times]{x03BC}$
m and assumed a linear regime between these two values. We used the LR continuum sensitivity (see Section 2.1.3), rescaled to the ultradeep survey, as standard deviation of the Gaussian noise that we included in the spectra. Figure 9 shows two of the simulated spectra. Finally, we exploit a modified version of the PAHFIT code (Smith et al. Reference Smith2007) that uses a power-law continuum, several PAH emission lines and silicate absorption, to fit the spectra and provide the source redshift (Negrello et al. in preparation). As shown in Figure 10, we find that we should be able to effectively recover the redshift in case of moderate and luminous type 2 AGN up to
$36\,\unicode[Times]{x03BC}$
m and assumed a linear regime between these two values. We used the LR continuum sensitivity (see Section 2.1.3), rescaled to the ultradeep survey, as standard deviation of the Gaussian noise that we included in the spectra. Figure 9 shows two of the simulated spectra. Finally, we exploit a modified version of the PAHFIT code (Smith et al. Reference Smith2007) that uses a power-law continuum, several PAH emission lines and silicate absorption, to fit the spectra and provide the source redshift (Negrello et al. in preparation). As shown in Figure 10, we find that we should be able to effectively recover the redshift in case of moderate and luminous type 2 AGN up to
![]() $z \sim 3{-}4$
. However, the code currently does not use AGN silicate
$z \sim 3{-}4$
. However, the code currently does not use AGN silicate
![]() $\,9.7\,\unicode[Times]{x03BC}$
m emission feature in finding the z and is proned to mis-interpret it as a PAH feature when it is strong; however, the code is still able to recover the redshift in case of faint AGN silicate emission line, as long as the silicate line is not mistakenly interpreted as a PAH feature. In particular, excluding three sources with strong Si
$\,9.7\,\unicode[Times]{x03BC}$
m emission feature in finding the z and is proned to mis-interpret it as a PAH feature when it is strong; however, the code is still able to recover the redshift in case of faint AGN silicate emission line, as long as the silicate line is not mistakenly interpreted as a PAH feature. In particular, excluding three sources with strong Si
![]() $\,9.7\,\unicode[Times]{x03BC}$
m emission features and one source with very low signal-to-noise ratio, we recovered the redshifts with a median error
$\,9.7\,\unicode[Times]{x03BC}$
m emission features and one source with very low signal-to-noise ratio, we recovered the redshifts with a median error
![]() $ |{z_{\rm best}-z_{\rm true}|\,/\,(1+z_{\rm true})} =0.02$
. In conclusion, a SPICA SMI-like instrument can provide us with low-resolution spectra for more than
$ |{z_{\rm best}-z_{\rm true}|\,/\,(1+z_{\rm true})} =0.02$
. In conclusion, a SPICA SMI-like instrument can provide us with low-resolution spectra for more than
![]() $6\,000$
AGN in a DEEP survey and, in the cases of sources with prominent host galaxy PAH lines and low AGN activity (i.e. unable to destroy these lines), measures of their spectroscopic redshifts. Moreover, it should be possible to obtain an estimate of the AGN obscuration from the depth of the silicate
$6\,000$
AGN in a DEEP survey and, in the cases of sources with prominent host galaxy PAH lines and low AGN activity (i.e. unable to destroy these lines), measures of their spectroscopic redshifts. Moreover, it should be possible to obtain an estimate of the AGN obscuration from the depth of the silicate
![]() $9.7\,\unicode[Times]{x03BC}$
m absorption feature (Wu et al. Reference Wu, Charmandaris, Huang, Spinoglio and Tommasin2009; Shi et al. Reference Shi2006 had shown that there is a correlation between these two quantities), that may provide support to the outcomes of X-ray spectroscopy in terms of obscuration (especially for low-statistics obscured AGN).
$9.7\,\unicode[Times]{x03BC}$
m absorption feature (Wu et al. Reference Wu, Charmandaris, Huang, Spinoglio and Tommasin2009; Shi et al. Reference Shi2006 had shown that there is a correlation between these two quantities), that may provide support to the outcomes of X-ray spectroscopy in terms of obscuration (especially for low-statistics obscured AGN).

Figure 9. Simulated SMI-LR spectra for a SPICA-like DEEP survey. Left panel is for
![]() $\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=43.9$
,
$\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=43.9$
,
![]() $\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=23.4$
(i.e. moderate-luminous obscured) AGN at
$\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=23.4$
(i.e. moderate-luminous obscured) AGN at
![]() $z=2$
; right panel for
$z=2$
; right panel for
![]() $\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=44.3$
,
$\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=44.3$
,
![]() $\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=24.1$
(i.e. high-luminous) CT-AGN
$\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=24.1$
(i.e. high-luminous) CT-AGN
![]() $z=2$
. We used the Lanzuisi et al. (Reference Lanzuisi2017) SEDs (inset in the upper left of the plots, where the red line is the AGN component, the blue one is related to the host galaxy, and the black one is the total AGN + galaxy emission) as spectral templates and added a white noise with amplitude based on the LR continuum sensitivity expected for a DEEP survey. The spectra were sampled with a resolution of
$z=2$
. We used the Lanzuisi et al. (Reference Lanzuisi2017) SEDs (inset in the upper left of the plots, where the red line is the AGN component, the blue one is related to the host galaxy, and the black one is the total AGN + galaxy emission) as spectral templates and added a white noise with amplitude based on the LR continuum sensitivity expected for a DEEP survey. The spectra were sampled with a resolution of
![]() $R=50$
at
$R=50$
at
![]() $17\,\unicode[Times]{x03BC}$
m and R
$17\,\unicode[Times]{x03BC}$
m and R
![]() $=120$
at
$=120$
at
![]() $36\,\unicode[Times]{x03BC}$
m.
$36\,\unicode[Times]{x03BC}$
m.

Figure 10. Redshift estimate from simulated SMI-LR-like spectra using a modified version of the PAHFIT code (Negrello et al. in preparation). Left panel is for
![]() $\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=43.9$
,
$\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=43.9$
,
![]() $\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=23.4$
moderate-luminous obscured AGN; right panel for
$\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=23.4$
moderate-luminous obscured AGN; right panel for
![]() $\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=44.3$
,
$\log{ (\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}=44.3$
,
![]() $\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=24.1$
high-luminous CT-AGN. We find that we should be able to effectively recover the redshift up to
$\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=24.1$
high-luminous CT-AGN. We find that we should be able to effectively recover the redshift up to
![]() $z \approx 3-4$
; at
$z \approx 3-4$
; at
![]() $z>4$
, there are too few strong PAH features in the SMI-LR wavelength range to allow a proper determination of the redshift.
$z>4$
, there are too few strong PAH features in the SMI-LR wavelength range to allow a proper determination of the redshift.
Focusing on the OSS capabilities, this instrument is able to exploit the above-mentioned mid-IR lines, but with the advantages of higher spectral resolution and larger wavelength range coverage than a SPICA-like instrument. Lines as the [Ne v]
![]() $14.3$
and
$14.3$
and
![]() $24.3\,\unicode[Times]{x03BC}$
m, [O iv]
$24.3\,\unicode[Times]{x03BC}$
m, [O iv]
![]() $25.9\,\unicode[Times]{x03BC}$
m, which are redshifted out of SMI-LR spectral range at modest redshift (
$25.9\,\unicode[Times]{x03BC}$
m, which are redshifted out of SMI-LR spectral range at modest redshift (
![]() $z < 1$
), thus requiring follow-ups with other instruments, can be detected up to very high-redshift, their detection being a matter of instrument sensitivity and not of limited wavelength range. Fine structure lines of O, C, Ne, S, N, Fe, Ar, and Si are keys to probe neutral and ionised gas phases and can be used to estimate redshift, amount of gas, its ionisation, presence of outflows, and the contribution of SF and AGN to the emission (Meixner et al. Reference Meixner2019; Mordini, Spinoglio, & Fernández-Ontiveros Reference Mordini, Spinoglio and Fernández-Ontiveros2021). The OSS DEEP survey will allow us to detect the PAH up to
$z < 1$
), thus requiring follow-ups with other instruments, can be detected up to very high-redshift, their detection being a matter of instrument sensitivity and not of limited wavelength range. Fine structure lines of O, C, Ne, S, N, Fe, Ar, and Si are keys to probe neutral and ionised gas phases and can be used to estimate redshift, amount of gas, its ionisation, presence of outflows, and the contribution of SF and AGN to the emission (Meixner et al. Reference Meixner2019; Mordini, Spinoglio, & Fernández-Ontiveros Reference Mordini, Spinoglio and Fernández-Ontiveros2021). The OSS DEEP survey will allow us to detect the PAH up to
![]() $z\approx4$
for galaxies with SFR
$z\approx4$
for galaxies with SFR
![]() $\sim\!10\,\text{M}_{\odot}\,\text{yr}^{-1}$
and over
$\sim\!10\,\text{M}_{\odot}\,\text{yr}^{-1}$
and over
![]() $z>6$
for those with SFR
$z>6$
for those with SFR
![]() $\sim\!100\,\text{M}_{\odot}\,\text{yr}^{-1}$
(Meixner et al. Reference Meixner2019). Regarding the estimate of the BHARD, the high sensitivity and large spectral range of the OSS survey will allow the detection of the [Ne v] line (whose flux correlates with the AGN intrinsic emission), as well as of the [O iv] and [Ne ii] line, whose line flux ratio can be used as a diagnostic of AGN power (e.g. Genzel et al. Reference Genzel1998; Lutz et al. Reference Lutz2003; Armus et al. Reference Armus2006; Armus et al. Reference Armus2007; Mordini et al. Reference Mordini, Spinoglio and Fernández-Ontiveros2021). Gruppioni et al. (Reference Gruppioni2016) well calibrated the relations between [Ne v] (or [O iv]) and AGN bolometric emission in samples of local galaxies. Bonato et al. (Reference Bonato2019) explored the spectroscopic survey capabilities of the OSS and find out that, in a DEEP survey, it can detect emission lines associated with SF up to
$\sim\!100\,\text{M}_{\odot}\,\text{yr}^{-1}$
(Meixner et al. Reference Meixner2019). Regarding the estimate of the BHARD, the high sensitivity and large spectral range of the OSS survey will allow the detection of the [Ne v] line (whose flux correlates with the AGN intrinsic emission), as well as of the [O iv] and [Ne ii] line, whose line flux ratio can be used as a diagnostic of AGN power (e.g. Genzel et al. Reference Genzel1998; Lutz et al. Reference Lutz2003; Armus et al. Reference Armus2006; Armus et al. Reference Armus2007; Mordini et al. Reference Mordini, Spinoglio and Fernández-Ontiveros2021). Gruppioni et al. (Reference Gruppioni2016) well calibrated the relations between [Ne v] (or [O iv]) and AGN bolometric emission in samples of local galaxies. Bonato et al. (Reference Bonato2019) explored the spectroscopic survey capabilities of the OSS and find out that, in a DEEP survey, it can detect emission lines associated with SF up to
![]() $z \approx 8.5$
and those of AGN emission, in particular [Ne v]
$z \approx 8.5$
and those of AGN emission, in particular [Ne v]
![]() $24.3\,\unicode[Times]{x03BC}$
m and [O iv]
$24.3\,\unicode[Times]{x03BC}$
m and [O iv]
![]() $25.9\,\unicode[Times]{x03BC}$
m, up to
$25.9\,\unicode[Times]{x03BC}$
m, up to
![]() $z \approx 3$
and
$z \approx 3$
and
![]() $z \approx 5$
, respectively.
$z \approx 5$
, respectively.
6.3. SED fitting
Working jointly, an IR cryogenic observatory, like SPICA or OST, and Athena can detect a huge fraction of the the AGN up to
![]() $z=10$
. The combined used of data from both wavelength bands will be fundamental, as with only IR photometric detections, it will not be possible to distinguish between the AGN and the galaxy emission, as SPICA SMI-CAM or OSS can measure only the total (AGN + host galaxy) emission, this in the lucky case of having already identified the source as an AGN. In this regard, a spectrometer similar to SPICA SMI-LR or OSS may surely help, but we will not be able to spectroscopically detect all the AGN, as the spectroscopic recovery fraction decreases rapidly for
$z=10$
. The combined used of data from both wavelength bands will be fundamental, as with only IR photometric detections, it will not be possible to distinguish between the AGN and the galaxy emission, as SPICA SMI-CAM or OSS can measure only the total (AGN + host galaxy) emission, this in the lucky case of having already identified the source as an AGN. In this regard, a spectrometer similar to SPICA SMI-LR or OSS may surely help, but we will not be able to spectroscopically detect all the AGN, as the spectroscopic recovery fraction decreases rapidly for
![]() $z>2$
. The additional use of other photometric data (such as those of B-BOP-like instruments, or from all the OSS bands), along with SED decomposition technique, could be used to overcome this limitation. Even in photometric mode, having six far-IR detections of OST will be invaluable in disentangling the AGN and host galaxy contribution: indeed, these bands cover both the regime where the torus has its peak emission and the regime where the SF is the main contributor to the SED. But we expect that the real game-changer in obscured AGN studies will come from a multi-wavelength approach.
$z>2$
. The additional use of other photometric data (such as those of B-BOP-like instruments, or from all the OSS bands), along with SED decomposition technique, could be used to overcome this limitation. Even in photometric mode, having six far-IR detections of OST will be invaluable in disentangling the AGN and host galaxy contribution: indeed, these bands cover both the regime where the torus has its peak emission and the regime where the SF is the main contributor to the SED. But we expect that the real game-changer in obscured AGN studies will come from a multi-wavelength approach.
The use of Athena data, optical, and near-IR photometric datapoints (in fields where these are already available, such as COSMOS and the Euclid Deep Fields), mid-IR, and far-IR photometric instruments (similar to those designed for SPICA) can provide a never-reached-before coverage of all the AGN and galaxy emission up to high redshift. In addition, with follow-up pointed spectroscopic observations of these targets (photometrically detected, but without a clear separation between galaxy and AGN components), we will be able to distinguish the AGN and host galaxy emissions using fine-structure lines and PAH features up to
![]() $z \sim 4$
(Spinoglio et al. Reference Spinoglio2021). Therefore, we expect to be able to improve our knowledge of the AGN
$z \sim 4$
(Spinoglio et al. Reference Spinoglio2021). Therefore, we expect to be able to improve our knowledge of the AGN
![]() $k_{\rm bol}-{L}_{bol}$
relation, similarly to what was done in Lusso et al. (Reference Lusso2012), but with a larger sample and to higher redshift. This should enable us to extend the
$k_{\rm bol}-{L}_{bol}$
relation, similarly to what was done in Lusso et al. (Reference Lusso2012), but with a larger sample and to higher redshift. This should enable us to extend the
![]() $k_{\rm bol}-{L}_{\rm bol}$
dynamical range and, having more sources, to reduce its uncertainties.
$k_{\rm bol}-{L}_{\rm bol}$
dynamical range and, having more sources, to reduce its uncertainties.
In Figure 7, we show the comparison of the total number of AGN detected by a SPICA-like observatory and by the OST OSS for a DEEP survey. The color code indicates the number of bands for which we can have photometric detection, considering SMI-CAM and the three B-BOP channel for SPICA and the six OSS bands for OST. For
![]() $z<2$
, both mission are able to detect almost all the sources in at least one band. While at
$z<2$
, both mission are able to detect almost all the sources in at least one band. While at
![]() $z>2$
SPICA begins to lose a fraction of the sources, OSS continues to detect them all up to
$z>2$
SPICA begins to lose a fraction of the sources, OSS continues to detect them all up to
![]() $z\approx 3.5$
.
$z\approx 3.5$
.
Moreover, having a sufficient number of photometric points would allow us to break the SF-AGN emission degeneracy and to estimate the AGN properties using SED-fitting decomposition techniques (jointly with additional instruments at different wavelengths) when spectra are not available. Although X-ray photometry and/or low-resolution spectroscopic data may not be used in SED fitting (but see X-CIGALE, Yang et al. Reference Yang2020), X-ray information could be crucial to select the templates to fit in the IR.
As a quick test for this statement, we simulated SPICA-like observations and used sed3fit to recover the stellar mass, SFR, and AGN bolometric luminosity. In particular, we selected a random sample of seventy sources among the
![]() ${\approx}550$
of the Lanzuisi et al. (Reference Lanzuisi2017) compilation that we used in this work and exploit sed3fit with up to 33 Laigle et al. (Reference Laigle2016) photometric data (from optical to sub-mm including Spitzer and Herschel, although not all the photometric points were available for all the sources) to obtain the AGN, host galaxy, and total SEDs. We used the total SEDs to estimate the SPICA SMI and B-BOP fluxes, added these four photometric points to the previous 33 and used all of them in new runs of sed3fit. We focused on the width of the 84–16th percentile of the probability distribution functions (PDFs) from sed3fit to check for the improvement provided by the use of SPICA-like data. We found that for, respectively, 50 and 45 of the 70 sources investigated, we have narrower AGN bolometric luminosity and SFR PDFs. The median SF relative error (i.e.
${\approx}550$
of the Lanzuisi et al. (Reference Lanzuisi2017) compilation that we used in this work and exploit sed3fit with up to 33 Laigle et al. (Reference Laigle2016) photometric data (from optical to sub-mm including Spitzer and Herschel, although not all the photometric points were available for all the sources) to obtain the AGN, host galaxy, and total SEDs. We used the total SEDs to estimate the SPICA SMI and B-BOP fluxes, added these four photometric points to the previous 33 and used all of them in new runs of sed3fit. We focused on the width of the 84–16th percentile of the probability distribution functions (PDFs) from sed3fit to check for the improvement provided by the use of SPICA-like data. We found that for, respectively, 50 and 45 of the 70 sources investigated, we have narrower AGN bolometric luminosity and SFR PDFs. The median SF relative error (i.e.
![]() $0.5\times(SFR_{84{{\rm th}}}-SFR_{16{\rm{th}}})/SFR_{\rm best}$
) improves from 11% to 1% and that of the AGN
$0.5\times(SFR_{84{{\rm th}}}-SFR_{16{\rm{th}}})/SFR_{\rm best}$
) improves from 11% to 1% and that of the AGN
![]() $L_{\rm bol}$
from 61% to 29%. The improvements in the stellar mass are smaller, since sed3fit estimates this parameter exploiting the optical wavelength band; therefore, we get only a minor advantage in using more IR data. The major improvements come from the cases where the AGN-SF degeneracies are stronger; as we can see from Figure 11, the additional mid- and far-IR points provided by a SPICA-like observatory help in disentangling the two contributions and allow us to obtain better estimates of both the host galaxy and AGN parameters (e.g. stellar mass, SFR, and AGN
$L_{\rm bol}$
from 61% to 29%. The improvements in the stellar mass are smaller, since sed3fit estimates this parameter exploiting the optical wavelength band; therefore, we get only a minor advantage in using more IR data. The major improvements come from the cases where the AGN-SF degeneracies are stronger; as we can see from Figure 11, the additional mid- and far-IR points provided by a SPICA-like observatory help in disentangling the two contributions and allow us to obtain better estimates of both the host galaxy and AGN parameters (e.g. stellar mass, SFR, and AGN
![]() $L_{\rm bolo}$
).
$L_{\rm bolo}$
).
6.4. CT-AGN
The search for CT-AGN is of fundamental importance in view of the still open questions of the missing sources responsible for the XRB and the galaxy co-evolution paradigm. About the former issue, XRB synthesis models predict a putative population of CT-AGN challenging to detect with current facilities (Gilli et al. Reference Gilli, Comastri and Hasinger2007, Reference Gilli2013; Harrison et al. Reference Harrison2016). In addition, the BH–galaxy co-evolution paradigm states that the scarcely known first phases of BH (and galaxy) growth should be associated with very obscured AGN activity and obscured SF; therefore, these elusive AGN are of the foremost importance to search for (e.g. Silk & Rees Reference Silk and Rees1998; Di Matteo et al. Reference Di Matteo, Springel and Hernquist2005; Lamastra et al. Reference Lamastra2013).
The adopted model for the XRB predicts that low-luminosity CT-AGN form the bulk of the very obscured AGN population. However, due to their large obscuration, it is difficult to detect them with X-ray instruments, while a SPICA-like (or OST) observatory should be able to effectively sample them with a detection fraction as high as 90% in the DEEP survey and 70% in the WIDE survey.

Figure 11. SED-fitting probability distribution functions (PDFs) for AGN 392925 (
![]() $\log{ (\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})}=45.0$
,
$\log{ (\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})}=45.0$
,
![]() $\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=24.1$
) at
$\log{ (\text{N}_{\text{H}}/\text{cm}^{-2})}=24.1$
) at
![]() $z=1.55$
. Left panel: AGN bolometric luminosity; right panel: SFR in the last 0.1 Gyr. The blue lines are obtained from the SED-fitting using 33 photometric bands from optical to far-IR (in particular, from IR telescope Spitzer and Herschel). The red lines are the PDFs obtained using the same 33 photometric bands plus the 4 simulated photometric observations of SPICA SMI-CAM, B-BOP1, B-BOP2, and B-BOP3. The use of the additional SPICA photometric points provides better constraints on the AGN bolometric power and, overall, allows us to properly disentangle the AGN and the SF emission.
$z=1.55$
. Left panel: AGN bolometric luminosity; right panel: SFR in the last 0.1 Gyr. The blue lines are obtained from the SED-fitting using 33 photometric bands from optical to far-IR (in particular, from IR telescope Spitzer and Herschel). The red lines are the PDFs obtained using the same 33 photometric bands plus the 4 simulated photometric observations of SPICA SMI-CAM, B-BOP1, B-BOP2, and B-BOP3. The use of the additional SPICA photometric points provides better constraints on the AGN bolometric power and, overall, allows us to properly disentangle the AGN and the SF emission.
As we can see from Figure 12, low-luminosity obscured AGN are difficult to detect even with the planned Athena facility. In fact, we estimated that Athena will be able to detect (light blue) more than half of all the high-luminosity CT-AGN, while the major part of the CT-AGN will be missed (
![]() $\sim\!20\%$
detection fraction), being low-luminosity sources (
$\sim\!20\%$
detection fraction), being low-luminosity sources (
![]() $\sim\!4\,260$
of the 5 200 CT-AGN per
$\sim\!4\,260$
of the 5 200 CT-AGN per
![]() $\mathrm{deg}^2$
have
$\mathrm{deg}^2$
have
![]() $\log(\mathrm{L_x/erg\,s^{-1}})< 43.5$
). The characterisation of these sources with Athena WFI (dotted area) will be challenging due to their low statistics: we may be able to recover
$\log(\mathrm{L_x/erg\,s^{-1}})< 43.5$
). The characterisation of these sources with Athena WFI (dotted area) will be challenging due to their low statistics: we may be able to recover
![]() $\text{L}_{\text{x}}$
and
$\text{L}_{\text{x}}$
and
![]() $\text{N}_{\text{H}}$
only for
$\text{N}_{\text{H}}$
only for
![]() $\sim\!6\,\%$
of the high-luminosity ones and
$\sim\!6\,\%$
of the high-luminosity ones and
![]() ${<}1\%$
for the low-luminosity. Sufficiently powerful IR surveys will be capable of detecting the reprocessed emission due to accretion at IR wavelengths. For example, a SPICA-like DEEP survey is capable of detecting (red areas)
${<}1\%$
for the low-luminosity. Sufficiently powerful IR surveys will be capable of detecting the reprocessed emission due to accretion at IR wavelengths. For example, a SPICA-like DEEP survey is capable of detecting (red areas)
![]() ${\approx}90\%$
of the CT-AGN and provide low-resolution spectra (shaded areas) for one-third of them. The even more powerful OST will allow us to detect photometrically (
${\approx}90\%$
of the CT-AGN and provide low-resolution spectra (shaded areas) for one-third of them. The even more powerful OST will allow us to detect photometrically (
![]() $R=4$
) almost all the CT-AGN and to have
$R=4$
) almost all the CT-AGN and to have
![]() $R=300$
spectra for at least half of them. Spectroscopic follow-up with other IR instruments will be fundamental in identifying CT-AGN with photometric detection but without a clear detection with SMI-LR-like or OSS instruments. Low-luminosity (high-luminosity) CT-AGN can be spectroscopically identified with a SAFARI-like instrument up to
$R=300$
spectra for at least half of them. Spectroscopic follow-up with other IR instruments will be fundamental in identifying CT-AGN with photometric detection but without a clear detection with SMI-LR-like or OSS instruments. Low-luminosity (high-luminosity) CT-AGN can be spectroscopically identified with a SAFARI-like instrument up to
![]() $z\sim 1.5$
(
$z\sim 1.5$
(
![]() $z\sim 2.5$
) and
$z\sim 2.5$
) and
![]() $z\sim 2.5$
(
$z\sim 2.5$
(
![]() $z > 4$
) via the [Ne v]
$z > 4$
) via the [Ne v]
![]() $24.3\,\unicode[Times]{x03BC}$
m and the [O iv]
$24.3\,\unicode[Times]{x03BC}$
m and the [O iv]
![]() $25.9\,\unicode[Times]{x03BC}$
m lines with 5-h observations (Spinoglio et al. Reference Spinoglio2021). Longer exposures (>10 h) will allow to identify CT-AGN beyond
$25.9\,\unicode[Times]{x03BC}$
m lines with 5-h observations (Spinoglio et al. Reference Spinoglio2021). Longer exposures (>10 h) will allow to identify CT-AGN beyond
![]() $z \sim 4$
. Despite the fact that the X-ray detection of these CT objects will be difficult, the Athena contribution to their study remains essential. In fact, only X-ray spectra (for individual sources or at least stacked X-ray data in case of no detection) can confirm the AGN nature of these sources (i.e. a flat X-ray continuum plus a strong iron line are clear indicators of heavy obscuration).
$z \sim 4$
. Despite the fact that the X-ray detection of these CT objects will be difficult, the Athena contribution to their study remains essential. In fact, only X-ray spectra (for individual sources or at least stacked X-ray data in case of no detection) can confirm the AGN nature of these sources (i.e. a flat X-ray continuum plus a strong iron line are clear indicators of heavy obscuration).

Figure 12. Number of CT AGN expected per
![]() $\mathrm{deg}^2$
and per
$\mathrm{deg}^2$
and per
![]() $\Delta z =1$
from a DEEP survey with Athena (left panels), with a SPICA-like observatory (middle panels), and with the OST OSS(right panels). The black lines are the total number of expected CT-AGN, the blue areas rapresent those which can be detected in the X-ray by Athena WFI and the dotted areas those for which we will be able to recover the
$\Delta z =1$
from a DEEP survey with Athena (left panels), with a SPICA-like observatory (middle panels), and with the OST OSS(right panels). The black lines are the total number of expected CT-AGN, the blue areas rapresent those which can be detected in the X-ray by Athena WFI and the dotted areas those for which we will be able to recover the
![]() $\text{L}_{\text{x}}$
and
$\text{L}_{\text{x}}$
and
![]() $\text{N}_{\text{H}}$
(with
$\text{N}_{\text{H}}$
(with
![]() $30\,\%$
uncertanties) using Athena WFI spectroscopy; the red areas represent those which can be detected in the IR with the SPICA SMI-CAM at 34
$30\,\%$
uncertanties) using Athena WFI spectroscopy; the red areas represent those which can be detected in the IR with the SPICA SMI-CAM at 34
![]() $\unicode[Times]{x03BC}$
m. The light red areas indicate that the host galaxy has the largest contribution to the flux in the SMI-CAM detection, while the dark red areas that the AGN is the dominant component. The dashed areas indicate that we will be able to have also mid-IR spectroscopic
$\unicode[Times]{x03BC}$
m. The light red areas indicate that the host galaxy has the largest contribution to the flux in the SMI-CAM detection, while the dark red areas that the AGN is the dominant component. The dashed areas indicate that we will be able to have also mid-IR spectroscopic
![]() $5\,\sigma$
detection with SPICA SMI-LR with a resolution
$5\,\sigma$
detection with SPICA SMI-LR with a resolution
![]() $R=50$
–120 in the 17–
$R=50$
–120 in the 17–
![]() $36\,\unicode[Times]{x03BC}$
m wavelength range. The light orange areas are the sources for which we expect detection in the OSS band 1 (25–
$36\,\unicode[Times]{x03BC}$
m wavelength range. The light orange areas are the sources for which we expect detection in the OSS band 1 (25–
![]() $44\,\unicode[Times]{x03BC}$
m) in photometric mode (
$44\,\unicode[Times]{x03BC}$
m) in photometric mode (
![]() $R=4$
), and the dark orange area those for which the AGN is the dominant component of the detected emission. The dashed areas refer to AGN for which we will have enough flux to have low-resolution (
$R=4$
), and the dark orange area those for which the AGN is the dominant component of the detected emission. The dashed areas refer to AGN for which we will have enough flux to have low-resolution (
![]() $R=300$
) spectra in OSS band 1. For the OST, we showed only the prediction for the band 1 of the OSS, but the instrument has five other bands (up to
$R=300$
) spectra in OSS band 1. For the OST, we showed only the prediction for the band 1 of the OSS, but the instrument has five other bands (up to
![]() $588\,\unicode[Times]{x03BC}$
m), for which we predict a larger number of AGN detected both in photometry and in spectrometry. The upper row refers to AGN with luminosity
$588\,\unicode[Times]{x03BC}$
m), for which we predict a larger number of AGN detected both in photometry and in spectrometry. The upper row refers to AGN with luminosity
![]() $42.0\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <42.5 $
, while the lower to those with
$42.0\le \log{(\text{L}_{\text{x}}/\text{erg}\,\text{s}^{-1})} <42.5 $
, while the lower to those with
![]() $43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <44.2$
.
$43.9\le \log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} <44.2$
.
For the most luminous ones, the combined use of Athena X-ray spectroscopy, mid-, and far-IR spectrophotometry (with SMI-CAM- and B-BOP-like instruments or with the OSS) will provide never achieved before insights of the intrinsic AGN emission and bolometric power and opportunities to sample them at redshift higher than the cosmic noon. As shown in Figure 13, at present, there are tensions between BHAD traced by X-rays, and those obtained by simulations, especially at
![]() $z > 2$
. At
$z > 2$
. At
![]() $z \sim 4$
, the BHAD expected from simulations (Aird et al. Reference Aird2015; Vito et al. Reference Vito2018) are
$z \sim 4$
, the BHAD expected from simulations (Aird et al. Reference Aird2015; Vito et al. Reference Vito2018) are
![]() $\sim\!5$
times higher than those computed via X-ray surveys, while actual IR surveys do not go beyond
$\sim\!5$
times higher than those computed via X-ray surveys, while actual IR surveys do not go beyond
![]() $z \sim 3$
. Different arguments, mostly driven by observations in the IR (Gruppioni et al. Reference Gruppioni2016; Bisigello et al. Reference Bisigello2020), predict a higher number of deeply obscured AGN, as for now undetected in the X-ray, that may alleviate this tension.
$z \sim 3$
. Different arguments, mostly driven by observations in the IR (Gruppioni et al. Reference Gruppioni2016; Bisigello et al. Reference Bisigello2020), predict a higher number of deeply obscured AGN, as for now undetected in the X-ray, that may alleviate this tension.

Figure 13. Redshift evolution of the BHAD adapted from Vito et al. (Reference Vito2018). The blue area is a theoretical BHAD curve obtained from Volonteri et al. (Reference Volonteri, Dubois, Pichon and Devriendt2016), Sijacki et al. (Reference Sijacki2015), and Shankar et al. (Reference Shankar, Weinberg and Miralda-Escudé2013). The red areas are the X-ray-derived BHADs, obtained from observations, from Aird et al. (Reference Aird2015), Ueda et al. (Reference Ueda, Akiyama, Hasinger, Miyaji and Watson2014), and Vito et al. (Reference Vito2014). The yellow area is the IR-derived BHAD from Delvecchio et al. (Reference Delvecchio2014). SPICA-like or OST missions will allow to sample the BHAD at higher z than actual IR survey and will be able to detect very obscured CT-AGN, missed by X-ray surveys, that should contribute to the total BHAD.
Exploiting all the capabilities of new generation IR cryogenic observatories (i.e. fast LR spectrophometry to detect and characterise low-redshift CT-AGN, spectroscopic follow-ups to identify those with only photometric detection, and multi-wavelength SED-fitting exploting already observed deep fields to separate the AGN and host galaxy emission) will allow us to discover the deeply obscured CT-AGN population up to very high redshift (
![]() $z > 4 $
). The presence of such an obscured population does not violate the limit imposed by the spectral energy density of the XRB, since these sources will provide an almost negligible contribution in the X-ray band (Comastri et al. Reference Comastri, Gilli, Marconi, Risaliti and Salvati2015). The updated picture, in terms of obscured accretion over cosmic time, that the IR missions discussed in this paper will lay out is fundamental in providing inputs to the simulations, which are still affected by considerable uncertainties and depend strongly on the adopted assumptions (e.g. González et al. Reference González2011; Jaacks et al. Reference Jaacks, Choi, Nagamine, Thompson and Varghese2012; Sijacki et al. Reference Sijacki2015; Shankar, Weinberg, & Miralda-Escudé Reference Shankar, Weinberg and Miralda-Escudé2013; Volonteri et al. Reference Volonteri, Dubois, Pichon and Devriendt2016; Thomas et al. Reference Thomas, Davé, Anglés-Alcázar and Jarvis2019).
$z > 4 $
). The presence of such an obscured population does not violate the limit imposed by the spectral energy density of the XRB, since these sources will provide an almost negligible contribution in the X-ray band (Comastri et al. Reference Comastri, Gilli, Marconi, Risaliti and Salvati2015). The updated picture, in terms of obscured accretion over cosmic time, that the IR missions discussed in this paper will lay out is fundamental in providing inputs to the simulations, which are still affected by considerable uncertainties and depend strongly on the adopted assumptions (e.g. González et al. Reference González2011; Jaacks et al. Reference Jaacks, Choi, Nagamine, Thompson and Varghese2012; Sijacki et al. Reference Sijacki2015; Shankar, Weinberg, & Miralda-Escudé Reference Shankar, Weinberg and Miralda-Escudé2013; Volonteri et al. Reference Volonteri, Dubois, Pichon and Devriendt2016; Thomas et al. Reference Thomas, Davé, Anglés-Alcázar and Jarvis2019).
7. Conclusions
In this work, we have investigated the capabilities of IR deep and wide surveys to detect and characterise AGN, as well as the advantages resulting by the synergies with the future X-ray observatory Athena. We used XRB synthesis models to predict the total number of AGN as a function of intrinsic X-ray luminosity, amount of obscuration, and redshift. A sample of more than 500 AGN from the COSMOS field with both X-ray spectra and optical-to-FIR SED-fitting has been used to investigate the AGN mid- and far-IR emission and to predict the fraction of AGN that will be detected by instrument similar to SPICA SMI, B-BOP, and the OST OSS. We compared the estimated total number of AGN with the fraction of those that will be detected by Athena, by a SPICA-like observatory and by the OST, with the goal of enlightening the synergies between X-ray and IR surveys in terms of detection and characterisation of AGN (in particular, of the most obscured ones) up to high redshift (i.e.
![]() $z\sim 10$
) and down to low luminosity (i.e.
$z\sim 10$
) and down to low luminosity (i.e.
![]() $\log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} \sim 42$
). In the IR bands, we also differentiated if we were primary detecting either the AGN or the host galaxy emission. Moreover, we investigated if we were able to spectroscopically identify and characterise the AGN emission with SMI-LR-like instruments or exploiting the full
$\log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} \sim 42$
). In the IR bands, we also differentiated if we were primary detecting either the AGN or the host galaxy emission. Moreover, we investigated if we were able to spectroscopically identify and characterise the AGN emission with SMI-LR-like instruments or exploiting the full
![]() $R=300$
spectral resolution of the OSS. In particular, we put emphasis on the elusive CT-AGN, a large fraction of those being missed by the current X-ray surveys, and that will require deep IR surveys for their detection and Athena spectra for their characterisation. Our main results are the following:
$R=300$
spectral resolution of the OSS. In particular, we put emphasis on the elusive CT-AGN, a large fraction of those being missed by the current X-ray surveys, and that will require deep IR surveys for their detection and Athena spectra for their characterisation. Our main results are the following:
-
1. An OST WIDE survey will be able to photometrically detect
 $\sim\!60\,\%$
of all the AGN in all the OSS bands and more than
$\sim\!60\,\%$
of all the AGN in all the OSS bands and more than
 $\sim\!80$
in at least one of the bands, while the DEEP survey will detect at least 95% of all the AGN at
$\sim\!80$
in at least one of the bands, while the DEEP survey will detect at least 95% of all the AGN at
 $z \le 10$
in at least one of the OSS bands and more than
$z \le 10$
in at least one of the OSS bands and more than
 $\sim\!80\%$
in all of them.
$\sim\!80\%$
in all of them. -
2. Considering an Athena and SPICA-like DEEP survey, we estimate that we can have both IR and X-ray detections for half of all the AGN and for more than the 80% of the high-luminosity (
 $\log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}\ge 43.5$
) AGN; for these sources just the Athena detection will assure us of the presence of AGN activity, even when the mid-IR torus contribution is diluted into the host galaxy emission. The Athena WFI spectral capabilities should also provide X-ray spectra, hence a reliable way to characterise the AGN, for thousands of AGN. This will allow us to estimate the AGN bolometric power and, having such a large number of sources with data in both the wavelength bands, to improve the AGN
$\log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})}\ge 43.5$
) AGN; for these sources just the Athena detection will assure us of the presence of AGN activity, even when the mid-IR torus contribution is diluted into the host galaxy emission. The Athena WFI spectral capabilities should also provide X-ray spectra, hence a reliable way to characterise the AGN, for thousands of AGN. This will allow us to estimate the AGN bolometric power and, having such a large number of sources with data in both the wavelength bands, to improve the AGN
 $L_{\text{mid-IR}}-\text{L}_{\text{x}}$
and
$L_{\text{mid-IR}}-\text{L}_{\text{x}}$
and
 $k_{\rm bol}-{L}_{\rm bol}$
relations. Moreover, the use of low-resolution spectra (such as those produce by a SMI-LR-like spectrometer), or alternatively, of mid- and far-IR photometric points (available with SMI-CAM- and B-BOP-like instruments) and SED-fitting decomposition technique, will help in constraining the AGN properties even in case of low-statistic X-ray spectra, like those we expect for very obscured and CT-AGN. However, even for sources with low photon statistics, the detection of a flat continuum and/or a strong iron emission line in the Athena WFI spectra will be invaluable clues to identify these sources as very obscured AGN.
$k_{\rm bol}-{L}_{\rm bol}$
relations. Moreover, the use of low-resolution spectra (such as those produce by a SMI-LR-like spectrometer), or alternatively, of mid- and far-IR photometric points (available with SMI-CAM- and B-BOP-like instruments) and SED-fitting decomposition technique, will help in constraining the AGN properties even in case of low-statistic X-ray spectra, like those we expect for very obscured and CT-AGN. However, even for sources with low photon statistics, the detection of a flat continuum and/or a strong iron emission line in the Athena WFI spectra will be invaluable clues to identify these sources as very obscured AGN. -
3. The sinergies of Athena with the OST are similar to those with a SPICA-like mission, but with the advantages of having up to six photometric point in the far-IR, a higher fraction (with respect to a SPICA-like mission) of sources with mid-IR spectra and providing
 $R=300$
, 25–
$R=300$
, 25–
 $588\,\unicode[Times]{x03BC}$
m spectra for
$588\,\unicode[Times]{x03BC}$
m spectra for
 $\sim\!50\%$
of all the AGN.
$\sim\!50\%$
of all the AGN. -
4. The CT-AGN, for which the X-ray detection and characterisation are challenging due to their high amount of obscuration, will be very well sampled by deep IR surveys. A SPICA-like DEEP survey should detect 86% of the low luminosity (
 $\log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} < 43.5$
) CT-AGN at
$\log{(\text{L}_{\text{x}}/\text{erg}\, \text{s}^{-1})} < 43.5$
) CT-AGN at
 $z \le 10$
, while, OST can provide with six mid- and far-IR photometric detections for a similar fraction of the AGN, and at least one band detection for more than
$z \le 10$
, while, OST can provide with six mid- and far-IR photometric detections for a similar fraction of the AGN, and at least one band detection for more than
 $\sim\!95\%$
of all the CT AGN at
$\sim\!95\%$
of all the CT AGN at
 $z<10$
. These kinds of missions would allow us to sample higher redshifts than what we are actually capable of at IR wavelengths, and detecting very obscured CT-AGN missed by X-ray surveys, to provide clues and possibly inputs to BHAD simulations. However, for most of these sources, the major contributor to the flux comes from the host galaxy emission, and the challenge will be to recognise them as AGN. In this context, pointed observations, such as those provided by SPICA SAFARI-like or OSS follow up, can be decisive in detecting the [Ne v]
$z<10$
. These kinds of missions would allow us to sample higher redshifts than what we are actually capable of at IR wavelengths, and detecting very obscured CT-AGN missed by X-ray surveys, to provide clues and possibly inputs to BHAD simulations. However, for most of these sources, the major contributor to the flux comes from the host galaxy emission, and the challenge will be to recognise them as AGN. In this context, pointed observations, such as those provided by SPICA SAFARI-like or OSS follow up, can be decisive in detecting the [Ne v]
 $24.3\,\unicode[Times]{x03BC}$
m and the [O iv]
$24.3\,\unicode[Times]{x03BC}$
m and the [O iv]
 $25.9\,\unicode[Times]{x03BC}$
m lines, which would allow us to unambiguously classify the source as an AGN.
$25.9\,\unicode[Times]{x03BC}$
m lines, which would allow us to unambiguously classify the source as an AGN. -
5. For high-luminosity CT-AGN, we will have X-ray detection with Athena up to
 $z \sim 3$
. This will allow us to to ascertain the AGN nature of these obscured sources and will provide vital input for the selection of IR SED templates and for their spectroscopic characterisation.
$z \sim 3$
. This will allow us to to ascertain the AGN nature of these obscured sources and will provide vital input for the selection of IR SED templates and for their spectroscopic characterisation. -
6. The use of mid- and far-IR photometric observations (such as those produced by SMI- and B-BOP-like instruments or by the OST OSS in
 $R=4$
photometric mode) can provide up to four (or six in the case of the OSS) photometric data points, which will be unique to improve the reliability of SED-fitting techniques to estimate the AGN properties up and beyond the cosmic noon.
$R=4$
photometric mode) can provide up to four (or six in the case of the OSS) photometric data points, which will be unique to improve the reliability of SED-fitting techniques to estimate the AGN properties up and beyond the cosmic noon. -
7. Mid-IR spectra are very helpful to recognise AGN and to separate their emission from the SF-related one. A SPICA-like observatory can provide LR spectra (with the SMI-LR instrument) for the majority of the detected objects at
 $z \le 2$
, and up to
$z \le 2$
, and up to
 $z\approx 4$
for the most luminous sources, as well as follow-up deep spectroscopy with SAFARI for galaxies up to and beyond
$z\approx 4$
for the most luminous sources, as well as follow-up deep spectroscopy with SAFARI for galaxies up to and beyond
 $z \sim 4$
. On the other hand, the OST OSS can deliver
$z \sim 4$
. On the other hand, the OST OSS can deliver
 $R=300$
, 25–
$R=300$
, 25–
 $588\,\unicode[Times]{x03BC}$
m spectra for
$588\,\unicode[Times]{x03BC}$
m spectra for
 $\sim\!50\%$
and
$\sim\!50\%$
and
 $\sim\!80\%$
of all the AGN with, respectively, its WIDE and DEEP surveys, the last one up to and beyond
$\sim\!80\%$
of all the AGN with, respectively, its WIDE and DEEP surveys, the last one up to and beyond
 $z \approx 4$
. The main spectral features to focus on will be the host galaxy PAH lines and the AGN
$z \approx 4$
. The main spectral features to focus on will be the host galaxy PAH lines and the AGN
 $9.7\,\unicode[Times]{x03BC}$
m silicate feature. We showed that, for what concerns the PAHs, those can be used to quickly recover the source spectroscopic redshift, without requiring specific higher-resolution follow-ups, while the silicate feature, when it is in absorption, jointly with X-ray spectral information, will allow us to assess and quantify the amount of obscuration. An Athena DEEP (WIDE) survey will provide X-ray spectral characterisation for
$9.7\,\unicode[Times]{x03BC}$
m silicate feature. We showed that, for what concerns the PAHs, those can be used to quickly recover the source spectroscopic redshift, without requiring specific higher-resolution follow-ups, while the silicate feature, when it is in absorption, jointly with X-ray spectral information, will allow us to assess and quantify the amount of obscuration. An Athena DEEP (WIDE) survey will provide X-ray spectral characterisation for
 ${\approx}20\%$
(
${\approx}20\%$
(
 ${\approx}6\%$
) of all the AGN and up to
${\approx}6\%$
) of all the AGN and up to
 ${\approx}50\%$
(
${\approx}50\%$
(
 ${\approx}21\%$
) of the high-luminosity ones, and, with the help of a multi-wavelengths approach, we will be able to characterise the properties even for X-ray low-statistic sources, such as CT-AGN.
${\approx}21\%$
) of the high-luminosity ones, and, with the help of a multi-wavelengths approach, we will be able to characterise the properties even for X-ray low-statistic sources, such as CT-AGN.
Mid- and far-IR deep surveys, such as those of a SPICA-like mission or of the OST, will allow us to fully exploit the potential of Athena for the measurement of the full Black Hole Accretion History, back to an age of the universe of
![]() $\sim1\,$
Gyr. This, along with the Star Formation History, will give us a much better understanding of galaxy evolution as compared to what we know today.
$\sim1\,$
Gyr. This, along with the Star Formation History, will give us a much better understanding of galaxy evolution as compared to what we know today.
Acknowledgements
This paper is dedicated to the memory of Bruce Swinyard, who initiated the SPICA project in Europe, but unfortunately died on 2015 May 22 at the age of 52 years. He was ISO-LWS calibration scientist, Herschel-SPIRE instrument scientist, first European PI of SPICA, and first design lead of SAFARI.
We acknowledge the whole SPICA Collaboration Team.
FP, CV, CG, LB, and LS acknowledge financial support by the Agenzia Spaziale Italiana (ASI) under the research contract 2018-31-HH.0. FJC acknowledges financial support from the Spanish Ministry MCIU under project RTI2018-096686-B-C21 (MCIU/AEI/FEDER/UE), cofunded by FEDER funds and from the Agencia Estatal de Investigación, Unidad de Excelencia María de Maeztu, ref. MDM-2017-0765. MPS acknowledges support from the Comunidad de Madrid, Spain, through Atracción de Talento Investigador Grant 2018-T1/TIC-11035 and PID2019-105423GA-I00 (MCIU/AEI/FEDER,UE). AF acknowledges the support from grant PRIN MIUR2017-20173ML3WW_001.
We also thank the SPICA Science Study Team appointed by ESA and the SPICA Galaxy Evolution Working Group. We should also thank here the Athena Science Study Team, also appointed by ESA, the Athena Science Working Groups Formation and growth of earliest SMBH and Understanding the build-up of SMBH and galaxies, and the Athena Community Office