1. Introduction
Migration of active matter is basic to our comprehension of diverse physiological environments, exemplified by phenomena like algal blooms (e.g. Durham & Stocker Reference Durham and Stocker2012). Specifically, the migration of confined micro-swimmers influences significantly environmental and bio-chemical processes, particularly in the context of dispersion and mixing (e.g. Cates & Tjhung Reference Cates and Tjhung2018; Gouiller et al. Reference Gouiller, Raynal, Maquet, Bourgoin, Cottin-Bizonne, Volk and Ybert2021). Nevertheless, a comprehensive theoretical depiction of the fundamental properties of living matter remains unattainable due to its profound complexity. It is plausible, therefore, that overarching principles such as conservation laws and symmetries serve as constraints on the potential collective behaviour exhibited by cells (Marchetti et al. Reference Marchetti, Joanny, Ramaswamy, Liverpool, Prost, Rao and Simha2013).
The dynamics of micro-swimmers is dominated by viscous forces at low Reynolds numbers, and their self-propulsion can occur only through non-reciprocal fluid manipulation (Purcell Reference Purcell1997). From a kinematic perspective, it is feasible to establish a linear relationship from force and moment matrices towards the velocity and rotation matrices through a grand resistance matrix that encompasses inherently a direct interplay between positional convective translation and orientational rotation (Karrila & Kim Reference Karrila and Kim1991). This progress could reveal mechanical and bio-physical properties of living matter at the level of each cell, for locomotion on small scales (Lauga Reference Lauga2011). On the other hand, there is an essential need for a phenomenological Smoluchowski approach on field-based continuum modelling, regarding the non-equilibrium steady state of an active system as emerging from the introduction of non-zero, albeit small, driving forces.
The homogenisation technique has been employed in various applications to investigate the long-term asymptotic dispersion of passive particles (Mei, Auriault & Ng Reference Mei, Auriault and Ng1996; Pavliotis Reference Pavliotis2008). Dispersion processes in confined flows, with reactions occurring either in the bulk or on a boundary, were investigated extensively by Ng & Yip (Ng Reference Ng2006a,Reference Ngb). Wu & Chen (Reference Wu and Chen2014) employed the homogenisation method to examine the initial stage and transverse concentration distributions. Despite progress in understanding the dispersion of passive particles, the homogenisation method has not been extended to investigate the dispersion of ellipsoidal micro-swimmers. In this work, an effective strategy involves categorising relaxation processes into fast and slow components. As vigorous applications and extensions, we formulate a homogenised theory that addresses primarily the slow dynamics, with the fast processes considered as sources of noise and damping.
Kumar et al. (Reference Kumar, Thomson, Powers and Harris2021) examined Taylor dispersion of passive ellipsoids with anisotropic diffusion at high flow Péclet numbers in a Poiseuille flow. Following the progress, asymptotic expressions of mean drift and dispersivity in the limit of large rotary Péclet numbers are derived by Khair (Reference Khair2022). In contrast to passive particles, the rotational dynamics turns out to be crucial, especially for the time-dependent transport of self-propelling micro-swimmers, because a slight deviation of the orientation could lead to markedly distinct distributions over brief time intervals. Anisotropic diffusion of ellipsoidal tracers in suspensions of active particles could display non-Gaussian statistics and dispersive phenomena (Nordanger, Morozov & Stenhammar Reference Nordanger, Morozov and Stenhammar2022). Rusconi, Guasto & Stocker (Reference Rusconi, Guasto and Stocker2014) showed that trajectories of bacteria displayed frequent loops in high-shear regions due to the hydrodynamic torque generated by the local shear, corresponding to a shear-induced trapping effect in the high-shear domains. Assuming that the steady distribution mirrors a uniform distribution and translational diffusion is negligible, Bearon, Hazel & Thorn (Reference Bearon, Hazel and Thorn2011) deduced a steady solution of the probability distribution for spheroidal gyrotactic micro-swimmers in a horizontal Poiseuille flow. Recently, Fung (Reference Fung2023) obtained analytical solutions for steady distributions of motile gyrotactic micro-organisms without translational diffusion in vertical flows. While the spatial and orientational dynamics of passive and active particles could be controlled under various mechanisms through external fields and/or fluctuations (Morris & Brady Reference Morris and Brady1996; Saintillan & Shelley Reference Saintillan and Shelley2013; Hwang & Pedley Reference Hwang and Pedley2014; Ishikawa & Pedley Reference Ishikawa and Pedley2014; Morris Reference Morris2020; Wang & Cirpka Reference Wang and Cirpka2021; Wang et al. Reference Wang, Jiang, Chen and Tao2022c; Yang et al. Reference Yang, Verzicco, Lohse and Caulfield2022; Zeng, Jiang & Pedley Reference Zeng, Jiang and Pedley2022), theory has not yet been developed in a general setting to address the migration of confined micro-swimmers experiencing both anisotropic diffusion and self-propulsion.
The interactions between active matter and rigid plates within the confined channel significantly influence a range of biophysical and chemical processes (Shen et al. Reference Shen, Farutin, Thiébaud and Misbah2017; Traverso & Michelin Reference Traverso and Michelin2022; Liao et al. Reference Liao, Erben, Kreysing and Lauga2023; Zhan, Jiang & Wu Reference Zhan, Jiang and Wu2024). The inclination of active suspensions to accumulate near surfaces is prominent (Rothschild Reference Rothschild1963). Hydrodynamic interaction, a potential but non-exclusive mechanism for migration, was addressed by Berke et al. (Reference Berke, Turner, Berg and Lauga2008) with regard to Escherichia coli. Alternatively, Li & Tang (Reference Li and Tang2009) proposed a kinematic-based mechanism that elucidates the accumulation phenomenon arising from bacterial collisions. This suggests that hydrodynamic interactions may play only a secondary role in the wall accumulation. The Smoluchowski equation could predict quantitatively the high-shear trapping phenomena (Bearon & Hazel Reference Bearon and Hazel2015). Nevertheless, in the absence of translational diffusion, non-physical concentration singularities may occur at walls. With periodic boundary conditions in position space, Vennamneni, Nambiar & Subramanian (Reference Vennamneni, Nambiar and Subramanian2020) concentrated on the trapping phenomena within low- and high-shear regions observed experimentally by Rusconi et al. (Reference Rusconi, Guasto and Stocker2014) and Barry et al. (Reference Barry, Rusconi, Guasto and Stocker2015), to exclude direct influences of channel plates.
The anisotropic diffusion of ellipsoidal particles is ubiquitous in nature, induced intrinsically by a non-spherical shape (Perrin Reference Perrin1936; Brenner Reference Brenner1967), as well as non-thermal fluctuations of an external force (Thiffeault & Guo Reference Thiffeault and Guo2022). Spatial fluctuations in viscosity give rise to modifications in both translation and rotation (Pedley Reference Pedley2010; Brumley et al. Reference Brumley, Polin, Pedley and Goldstein2015; Chen, Perazzo & Stone Reference Chen, Perazzo and Stone2020; Kamal & Lauga Reference Kamal and Lauga2023). By abstracting the mechanism underlying speed alterations and reorientation, a field-based model could capture adeptly these dynamic phenomena. Shear-induced migration of active ellipsoids uncovers abundant counter-intuitive phenomena, e.g. low-shear trapping (Rusconi et al. Reference Rusconi, Guasto and Stocker2014; Vennamneni et al. Reference Vennamneni, Nambiar and Subramanian2020), upstream rheotaxis (Hill et al. Reference Hill, Kalkanci, McMurry and Koser2007; Kaya & Koser Reference Kaya and Koser2009; Omori et al. Reference Omori, Kikuchi, Schmitz, Pavlovic, Chuang and Ishikawa2022) and centreline depletion (Rusconi et al. Reference Rusconi, Guasto and Stocker2014; Ezhilan & Saintillan Reference Ezhilan and Saintillan2015), etc. Inspired by these recent experimental and theoretical investigations, we attempt to analyse at a population level the shear-induced migration of active ellipsoids subject to coupled diffusivities within a continuum theoretical framework. Intriguingly, how could built-in asymmetries and external driving forces modify the migration of confined micro-swimmers?
The paper is structured as follows. Section 2 presents the Smoluchowski analysis for confined micro-swimmers with anisotropic diffusion, followed in § 3 by asymptotic solutions for steady moments and macroscopic transport coefficients. Effects of anisotropic diffusion, particle shape anisotropy, external fields and self-propulsion on the obtained concentration and orientation distributions are considered in § 4, as well as the transient phenomenological transport coefficients in § 5. Finally, § 6 concludes. Solution procedures of time-dependent distributions can be found in Appendix A, and numerical validations through the Monte Carlo method are shown in Appendix B.
2. Problem formulation
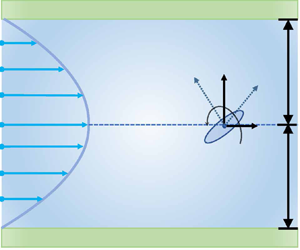
We consider a dilute suspension of confined micro-swimmers in a steady parallel flow subject to anisotropic diffusion. Ellipsoidal micro-swimmers are exemplified with fluctuations in both position and orientation spaces, of which the origins could be athermal and biological. A set of two-dimensional Cartesian coordinates ![]() $\boldsymbol {R}=[x, z]^{\rm T}$ with base vectors
$\boldsymbol {R}=[x, z]^{\rm T}$ with base vectors ![]() $({\boldsymbol {e}}_{x}, {\boldsymbol {e}}_{z})$ is introduced, as shown in figure 1. A statistical mechanical description of a particle's motion is embodied in the probability distribution function
$({\boldsymbol {e}}_{x}, {\boldsymbol {e}}_{z})$ is introduced, as shown in figure 1. A statistical mechanical description of a particle's motion is embodied in the probability distribution function ![]() $P(\boldsymbol {R},\theta, t)$ of finding the swimmer at the right position at time
$P(\boldsymbol {R},\theta, t)$ of finding the swimmer at the right position at time ![]() $t$, with
$t$, with ![]() $\theta$ standing for the angle of the orientation vector
$\theta$ standing for the angle of the orientation vector ![]() ${\boldsymbol {p}}$ from the positive
${\boldsymbol {p}}$ from the positive ![]() $z$-axis. The transport problem adopts the form of the Smoluchowski equation in the position and orientation spaces, from the conservation law of mass as
$z$-axis. The transport problem adopts the form of the Smoluchowski equation in the position and orientation spaces, from the conservation law of mass as
where ![]() $\boldsymbol {\nabla }_{\boldsymbol {R}}$ is the gradient operator in the position space,
$\boldsymbol {\nabla }_{\boldsymbol {R}}$ is the gradient operator in the position space, ![]() ${\boldsymbol {U}_f(\boldsymbol {R})}=[U_f(\boldsymbol {R}),0]^{\rm T}$ is the external velocity. We parameterise all length scales by the width
${\boldsymbol {U}_f(\boldsymbol {R})}=[U_f(\boldsymbol {R}),0]^{\rm T}$ is the external velocity. We parameterise all length scales by the width ![]() $W^*$ of the channel, flow velocity
$W^*$ of the channel, flow velocity ![]() $U_f^*$ by the mean speed
$U_f^*$ by the mean speed ![]() $U_m^*$ over the lateral cross-section, swimming velocity by the swimming speed
$U_m^*$ over the lateral cross-section, swimming velocity by the swimming speed ![]() $V_s^*$ of active ellipsoids, the rate of orientational change
$V_s^*$ of active ellipsoids, the rate of orientational change ![]() $\varOmega ^*$ by the rotational diffusivity
$\varOmega ^*$ by the rotational diffusivity ![]() $D_\theta ^*$, and dimensional translational diffusivities
$D_\theta ^*$, and dimensional translational diffusivities ![]() $(D_{\|}^*$ and
$(D_{\|}^*$ and ![]() $D_{\perp }^*)$ along the parallel and perpendicular axes by
$D_{\perp }^*)$ along the parallel and perpendicular axes by ![]() $D_\theta ^* W^{* 2}$, with asterisk signs employed to represent the dimensional characteristic quantities. Specifically, the dimensionless parameters are
$D_\theta ^* W^{* 2}$, with asterisk signs employed to represent the dimensional characteristic quantities. Specifically, the dimensionless parameters are
 \begin{equation} \left. \begin{gathered} t=t^* D_\theta^*, \quad x=\frac{x^*-U_m^* t^*}{W^*}, \quad z=\frac{z^*}{W^*}, \quad U_f=\frac{U_f^*}{U_m^*}-1, \quad \varOmega=\frac{\varOmega^*}{D_\theta^*},\\ {{Pe}}_s= \frac{V_s^*}{D_\theta^* W^*},\quad {{Pe}}_f=\frac{U_m^*}{D_\theta^* W^*}, \quad D_{\|}=\frac{D_{\|}^{*}}{D_\theta^*W^{*2}},\quad D_{{\perp}}=\frac{D_{{\perp}}^{*}}{D_\theta^*W^{*2}}, \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} t=t^* D_\theta^*, \quad x=\frac{x^*-U_m^* t^*}{W^*}, \quad z=\frac{z^*}{W^*}, \quad U_f=\frac{U_f^*}{U_m^*}-1, \quad \varOmega=\frac{\varOmega^*}{D_\theta^*},\\ {{Pe}}_s= \frac{V_s^*}{D_\theta^* W^*},\quad {{Pe}}_f=\frac{U_m^*}{D_\theta^* W^*}, \quad D_{\|}=\frac{D_{\|}^{*}}{D_\theta^*W^{*2}},\quad D_{{\perp}}=\frac{D_{{\perp}}^{*}}{D_\theta^*W^{*2}}, \end{gathered} \right\} \end{equation}
wherein ![]() $D_\|$ is the dimensionless translational diffusivity parallel to the swimming direction,
$D_\|$ is the dimensionless translational diffusivity parallel to the swimming direction, ![]() $D_{\perp }$ is the dimensionless translational diffusivity perpendicular to the swimming direction,
$D_{\perp }$ is the dimensionless translational diffusivity perpendicular to the swimming direction, ![]() ${{Pe}}_s$ is the dimensionless swim Péclet number and
${{Pe}}_s$ is the dimensionless swim Péclet number and ![]() ${{Pe}}_f$ is the dimensionless flow Péclet number. Provided inertial motion and particle–particle interaction are absent, the angular velocity could be determined through Jeffery's formulation (Jeffery & Filon Reference Jeffery and Filon1922; Leal & Hinch Reference Leal and Hinch1972; Pedley & Kessler Reference Pedley and Kessler1992; Lauga Reference Lauga2020), so that the rate of change of orientation is
${{Pe}}_f$ is the dimensionless flow Péclet number. Provided inertial motion and particle–particle interaction are absent, the angular velocity could be determined through Jeffery's formulation (Jeffery & Filon Reference Jeffery and Filon1922; Leal & Hinch Reference Leal and Hinch1972; Pedley & Kessler Reference Pedley and Kessler1992; Lauga Reference Lauga2020), so that the rate of change of orientation is
where ![]() $\alpha _0= (AR^2-1)/(AR^2+1)$ is the shape factor characterised by the aspect ratio
$\alpha _0= (AR^2-1)/(AR^2+1)$ is the shape factor characterised by the aspect ratio ![]() $AR$,
$AR$, ![]() $\lambda =1/2B^*D_\theta ^*$ is the gyrotactic bias parameter and
$\lambda =1/2B^*D_\theta ^*$ is the gyrotactic bias parameter and ![]() $B^*$ is the reorientation time. Specifically,
$B^*$ is the reorientation time. Specifically, ![]() $\alpha _0=0$ stands for spheroids and
$\alpha _0=0$ stands for spheroids and ![]() $\alpha _0=1$ for infinitely thin rods. The elements of the translational diffusivity tensor are
$\alpha _0=1$ for infinitely thin rods. The elements of the translational diffusivity tensor are

Figure 1. Ellipsoidal micro-swimmers suspended in a Poiseuille flow subject to anisotropic Brownian diffusion and an external gravity field.
In this context, the present work extends the existing theory concerning macro-transport processes (Jiang & Chen Reference Jiang and Chen2021; Wang, Jiang & Chen Reference Wang, Jiang and Chen2022b; Guan et al. Reference Guan, Jiang, Wang, Zeng, Li and Chen2023), facilitating the direct interplay of convection and diffusion in the local and global spaces. The transport of active ellipsoids, characterised by anisotropic diffusion, becomes intricate due to the influence of cross-diffusivities.
The no-flux boundary conditions require
Provided that collisions between ellipsoids and channel boundaries are perfectly elastic, we further require in the position space that the incident probability fluxes be compensated by the reflected fluxes as (Bearon et al. Reference Bearon, Hazel and Thorn2011; Volpe, Gigan & Volpe Reference Volpe, Gigan and Volpe2014; Ezhilan & Saintillan Reference Ezhilan and Saintillan2015; Jakuszeit, Croze & Bell Reference Jakuszeit, Croze and Bell2019)
We refer to (2.6–2.7) as reflective boundary conditions in what follows of our derivation. For clarity, no periodic boundary conditions are applied at ![]() $z=0$ and
$z=0$ and ![]() $z=1$. It can be verified with simple algebra that the reflective boundary conditions satisfy the no-flux integral condition (2.5). From individual Brownian dynamics, when a micro-swimmer hits the boundary, the swimmer changes symmetrically the swimming direction and bounces off like a billiard. This strong condition might be realised via reasonable control strategies for artificial nano- and micro-robots, yet it is seemingly unrealistic for alive motile micro-organisms. In the orientation space, periodic boundary conditions are imposed as
$z=1$. It can be verified with simple algebra that the reflective boundary conditions satisfy the no-flux integral condition (2.5). From individual Brownian dynamics, when a micro-swimmer hits the boundary, the swimmer changes symmetrically the swimming direction and bounces off like a billiard. This strong condition might be realised via reasonable control strategies for artificial nano- and micro-robots, yet it is seemingly unrealistic for alive motile micro-organisms. In the orientation space, periodic boundary conditions are imposed as
The initial probability distribution ![]() $P^{(0)}$ is given as
$P^{(0)}$ is given as
where ![]() $P^{(0)}$ is a prescribed distribution function.
$P^{(0)}$ is a prescribed distribution function.
We introduce a differential operator defined as
with reflective boundary conditions in the ![]() $z$-space and periodic boundary conditions in the
$z$-space and periodic boundary conditions in the ![]() $\theta$-space. Note that the linear operator
$\theta$-space. Note that the linear operator ![]() $\mathcal {L}$ is not self-adjoint if
$\mathcal {L}$ is not self-adjoint if ![]() $\varOmega \neq 0$ or
$\varOmega \neq 0$ or ![]() ${{Pe}} \neq 0$. The transport equation (2.1) for the probability distribution function could thus be re-written as
${{Pe}} \neq 0$. The transport equation (2.1) for the probability distribution function could thus be re-written as
Further coupling of the external field (e.g. force fields) between the global (streamwise) and local spaces could be introduced in the meantime, which does not break the generality of the manipulation discussed hereafter by absorbing the external field into the velocity terms. It is supposed the coupled diffusivities are symmetrical,
as embodied in (2.4). When these coupled diffusing terms are set to zero, the resulting transport problem reduces to the special case in the existing dispersion analysis of active particles (Jiang & Chen Reference Jiang and Chen2019). As a substantial extension of the previous dispersion theory, the present case is more general by including the direct coupling between global and local transport processes.
3. Asymptotic solutions of macro-transport processes with anisotropic diffusion
Here, we proceed to evaluate the anisotropic diffusion of micro-swimmers by a homogenisation method. Since only the effects of local translational diffusivity in the lateral direction enter into the local operator, any coupling fluctuations of micro-swimmers can be neglected safely, to the leading order. That is, the relevant diffusivity component at the leading order only arises in the vertical direction, while the cross-diffusivities act in the sequence of higher orders. Some formal transformations are considered below.
3.1. General considerations on macro-transport processes subject to anisotropic diffusion
Note that, due to the convection term by the shear flow, the solution of (2.12) will have the form of a mass cloud moving to infinity at long times. Thus, we hereafter study the solution ![]() $P(x^\prime,t)=P(x- \bar {U}t,t)$ in a moving coordinate, where
$P(x^\prime,t)=P(x- \bar {U}t,t)$ in a moving coordinate, where ![]() $\bar {U}$ is the drift to be quantified. Then, the transport equation of the probability density function turns into
$\bar {U}$ is the drift to be quantified. Then, the transport equation of the probability density function turns into
Given the slow variation in both the initial distribution and its corresponding solution, it is appropriate to investigate the system's effective dynamics on the extended space and time scales. In this work, we present a small parameter ![]() $\epsilon$ as the ratio of the local Péclet number to the global Péclet number. Here, the limit
$\epsilon$ as the ratio of the local Péclet number to the global Péclet number. Here, the limit ![]() $\epsilon \rightarrow 0$ corresponds to the asymptotically long times during which a single particle samples the entire local spaces (
$\epsilon \rightarrow 0$ corresponds to the asymptotically long times during which a single particle samples the entire local spaces (![]() $z$- and
$z$- and ![]() $\theta$-spaces) at a longitudinal position before spreading downstream. The local Péclet number can be manifested as the collective influence of translational diffusion along parallel, perpendicular and/or cross directions in the local position space, as well as rotational diffusion in the orientation space. Nevertheless, the combined effect of local aspects is typically overshadowed by the influence of the global (longitudinal) Péclet number. As the convective field tends to an average of zero, the resultant behaviour of
$\theta$-spaces) at a longitudinal position before spreading downstream. The local Péclet number can be manifested as the collective influence of translational diffusion along parallel, perpendicular and/or cross directions in the local position space, as well as rotational diffusion in the orientation space. Nevertheless, the combined effect of local aspects is typically overshadowed by the influence of the global (longitudinal) Péclet number. As the convective field tends to an average of zero, the resultant behaviour of ![]() $P$ mirrors that characteristic of a pure diffusion process. To address this effect, we resort to the following particular scaling of space and time about
$P$ mirrors that characteristic of a pure diffusion process. To address this effect, we resort to the following particular scaling of space and time about ![]() $\epsilon$ as:
$\epsilon$ as:
This scale separation, known as the diffusive scaling (Pavliotis Reference Pavliotis2008, Chapter 13, p. 210), is anticipated for asymptotically long times, to yield the effective drift and diffusivity. The reason for different scales of perturbation in time and space is that this treatment homogenises the local spaces for the derivation of an effective diffusion equation, as could be placed into evidence promptly should we initially approximate an ![]() $\epsilon$ scale for both time and space before coming to the present scale separation successively. Now the rescaled probability distribution
$\epsilon$ scale for both time and space before coming to the present scale separation successively. Now the rescaled probability distribution ![]() $P^\epsilon$ as spatio-temporal functions of
$P^\epsilon$ as spatio-temporal functions of ![]() $\xi$ and
$\xi$ and ![]() $\tau$ satisfies the equation
$\tau$ satisfies the equation
Assuming that the probability distribution ![]() $P$ possesses an a posteriori unique solution, substitution of an approximate solution of multiple-scale expansions in the limit of
$P$ possesses an a posteriori unique solution, substitution of an approximate solution of multiple-scale expansions in the limit of ![]() $\epsilon \rightarrow 0$
$\epsilon \rightarrow 0$
into (3.3) gives a hierarchy of equations, belonging to the framework of the classical homogenisation problem.
Let us collect the terms of order 1 as
Since the longitudinal distribution of the initial condition is a function independent of the small-scale variable ![]() $\xi$, it is intuitive to conclude that the leading-order behaviour should be a function only of
$\xi$, it is intuitive to conclude that the leading-order behaviour should be a function only of ![]() $z$ and
$z$ and ![]() $\theta$. Next, we equate to zero the terms of the order of
$\theta$. Next, we equate to zero the terms of the order of ![]() $\epsilon ^1$
$\epsilon ^1$
A separation of variables for the first moment will then yield a cell problem of ![]() $b(z,\theta )$, which contains complete local information.
$b(z,\theta )$, which contains complete local information.
Although the coupling of components of the diffusivity tensor breaks the independence between the global and local spaces, the Onsager-like symmetry relations guarantee the mathematical tractability for the cross-diffusivities, i.e. the transposes of the global, local and coupling diffusion tensors equal themselves. For the order of ![]() $\epsilon ^2$, we have
$\epsilon ^2$, we have
These equations will be solved recursively below.
3.2. Perturbations of zeroth order
For the equation of the order of 1, a transient separable solution is
with ![]() $\mathcal {L} P_{0}^{\infty } =0$. That is, the historical effect is shown as
$\mathcal {L} P_{0}^{\infty } =0$. That is, the historical effect is shown as ![]() $c( \xi,\tau )$. At the leading order, the probability density is similar to the classical theory (Brenner & Edwards Reference Brenner and Edwards1993; Jiang & Chen Reference Jiang and Chen2019) subject to isotropic diffusion, albeit with the lateral translational diffusivity opting for its local value.
$c( \xi,\tau )$. At the leading order, the probability density is similar to the classical theory (Brenner & Edwards Reference Brenner and Edwards1993; Jiang & Chen Reference Jiang and Chen2019) subject to isotropic diffusion, albeit with the lateral translational diffusivity opting for its local value.
Specifically, the governing equations of ![]() $P_0^\infty$ are
$P_0^\infty$ are
 \begin{equation}
\left. \begin{gathered} \mathcal{L} P_0^{\infty}=0,\\ P_0^{\infty}
\left(z,\theta\right)=P_0^{\infty}
\left(z,{\rm \pi}-\theta\right), \quad \text{ at } z=0,1, \\
\frac{\partial P_0^{\infty}}{\partial z}
\left(z,\theta\right)={-}\frac{\partial P_0^{\infty}}{\partial z}
\left(z,{\rm \pi}-\theta\right),
\quad \text{ at } z=0,1, \\
\left.P_0^{\infty}\right|_{\theta=0}=\left.P_0^{\infty}\right|_{\theta=2
{\rm \pi}}, \\ \left.\frac{\partial P_0^{\infty}}{\partial
\theta}\right|_{\theta=0}=\left.\frac{\partial
P_0^{\infty}}{\partial \theta}\right|_{\theta=2 {\rm \pi}}.
\end{gathered} \right\}
\end{equation}
\begin{equation}
\left. \begin{gathered} \mathcal{L} P_0^{\infty}=0,\\ P_0^{\infty}
\left(z,\theta\right)=P_0^{\infty}
\left(z,{\rm \pi}-\theta\right), \quad \text{ at } z=0,1, \\
\frac{\partial P_0^{\infty}}{\partial z}
\left(z,\theta\right)={-}\frac{\partial P_0^{\infty}}{\partial z}
\left(z,{\rm \pi}-\theta\right),
\quad \text{ at } z=0,1, \\
\left.P_0^{\infty}\right|_{\theta=0}=\left.P_0^{\infty}\right|_{\theta=2
{\rm \pi}}, \\ \left.\frac{\partial P_0^{\infty}}{\partial
\theta}\right|_{\theta=0}=\left.\frac{\partial
P_0^{\infty}}{\partial \theta}\right|_{\theta=2 {\rm \pi}}.
\end{gathered} \right\}
\end{equation}
The asymptotic zeroth moment ![]() $P_0^{\infty }$ can be determined explicitly by solving the above equation set. Benchmark solutions of
$P_0^{\infty }$ can be determined explicitly by solving the above equation set. Benchmark solutions of ![]() $P_0^{\infty }$ will be shown for some special cases shortly. When it comes to more general cases with particle shape anisotropy and a coupling diffusivity tensor, the zeroth moment can be derived as a series expansion of the eigenfunctions. A Galerkin solution is pursued for
$P_0^{\infty }$ will be shown for some special cases shortly. When it comes to more general cases with particle shape anisotropy and a coupling diffusivity tensor, the zeroth moment can be derived as a series expansion of the eigenfunctions. A Galerkin solution is pursued for ![]() $P_0^{\infty }$ as
$P_0^{\infty }$ as
 \begin{align} P_0^{\infty}(z,\theta) &=\sum_{i=1}^{\infty} q_i e_i(z,\theta) \nonumber\\ &\equiv \sum_{i=0}^{\infty }\sum_{j=1}^{\infty } \left[ A_{ij} \cos (i{\rm \pi} z)+B_{ij} \cos (i{\rm \pi} z)\cos (j\theta)+ C_{ij} \sin (i{\rm \pi} z)\sin (j\theta)\right], \end{align}
\begin{align} P_0^{\infty}(z,\theta) &=\sum_{i=1}^{\infty} q_i e_i(z,\theta) \nonumber\\ &\equiv \sum_{i=0}^{\infty }\sum_{j=1}^{\infty } \left[ A_{ij} \cos (i{\rm \pi} z)+B_{ij} \cos (i{\rm \pi} z)\cos (j\theta)+ C_{ij} \sin (i{\rm \pi} z)\sin (j\theta)\right], \end{align}
in which ![]() $A_{ij}$,
$A_{ij}$, ![]() $B_{ij}$ and
$B_{ij}$ and ![]() $C_{ij}$ are the coefficients to be obtained by a group of linear equations with the orthogonality of trigonometric functions, and
$C_{ij}$ are the coefficients to be obtained by a group of linear equations with the orthogonality of trigonometric functions, and ![]() $q_i$ is the abstract coefficient vector. The analytical approximation would be truncated at a finite number, for the computational effectiveness of
$q_i$ is the abstract coefficient vector. The analytical approximation would be truncated at a finite number, for the computational effectiveness of ![]() $P_0^\infty$. Due to the potential non-self-adjoint nature of
$P_0^\infty$. Due to the potential non-self-adjoint nature of ![]() $\mathcal {L}$, a weak formulation is given in the form of an inner product. By computing in advance the inner product of
$\mathcal {L}$, a weak formulation is given in the form of an inner product. By computing in advance the inner product of ![]() $e_i$ and
$e_i$ and ![]() $\mathcal {L}e_j$ in a bi-linear form, the problem turns into solving the null space of the local operator. That is, the coefficients are determined by the obtained null vector with an arbitrary constant. The normalisation condition
$\mathcal {L}e_j$ in a bi-linear form, the problem turns into solving the null space of the local operator. That is, the coefficients are determined by the obtained null vector with an arbitrary constant. The normalisation condition
will ascertain the coefficients to be unique, wherein the averaging operator is defined as
3.3. Perturbations of first order
At ![]() $\textit {O}(\epsilon )$, the no-flux boundary condition becomes
$\textit {O}(\epsilon )$, the no-flux boundary condition becomes
With (3.6), (3.13) and corresponding periodic boundary conditions, a centring condition is
 \begin{align}
&\left\langle -\left[ P{{e}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta
-{{{\bar{U}}}} \right] \frac{\partial P_{0}}{\partial
\xi}+2{{D}_{xz}}\frac{\partial^2 P_{0}}{\partial \xi
\partial z} \right\rangle \nonumber\\ &\quad =\langle
\mathcal{L} P_1\rangle\nonumber\\ &\quad= \left\langle
{{Pe}}_s \cos \theta \frac{\partial
P_1}{\partial z} +\frac{\partial \left[ \varOmega(z,
\theta) P_1 \right]}{\partial \theta}
-2D_{xz}(\theta)\frac{\partial^2 P_0}{\partial \xi \partial
z} -D_{zz}(\theta)\frac{\partial^2 P_1}{\partial z^2}
-\frac{\partial^2 P_1}{\partial \theta^2}
\right\rangle\nonumber\\ &\quad ={-}\int_{0}^{1}
\,\mathrm{d}z \int_{0}^{2{\rm \pi}} \frac{\partial}{\partial z}
\left[2D_{xz}(\theta)\frac{\partial P_0}{\partial \xi}
+D_{zz}(\theta)\frac{\partial P_1}{\partial
z}-{{Pe}}_s \cos \theta P_1 \right]
\,\mathrm{d}\theta\nonumber\\ &\qquad+\int_{0}^{1}
\mathrm{d}z \left[\varOmega(z, \theta) P_1- \frac{\partial
P_1}{\partial \theta}\right]_0^{2{\rm \pi}} =0.
\end{align}
\begin{align}
&\left\langle -\left[ P{{e}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta
-{{{\bar{U}}}} \right] \frac{\partial P_{0}}{\partial
\xi}+2{{D}_{xz}}\frac{\partial^2 P_{0}}{\partial \xi
\partial z} \right\rangle \nonumber\\ &\quad =\langle
\mathcal{L} P_1\rangle\nonumber\\ &\quad= \left\langle
{{Pe}}_s \cos \theta \frac{\partial
P_1}{\partial z} +\frac{\partial \left[ \varOmega(z,
\theta) P_1 \right]}{\partial \theta}
-2D_{xz}(\theta)\frac{\partial^2 P_0}{\partial \xi \partial
z} -D_{zz}(\theta)\frac{\partial^2 P_1}{\partial z^2}
-\frac{\partial^2 P_1}{\partial \theta^2}
\right\rangle\nonumber\\ &\quad ={-}\int_{0}^{1}
\,\mathrm{d}z \int_{0}^{2{\rm \pi}} \frac{\partial}{\partial z}
\left[2D_{xz}(\theta)\frac{\partial P_0}{\partial \xi}
+D_{zz}(\theta)\frac{\partial P_1}{\partial
z}-{{Pe}}_s \cos \theta P_1 \right]
\,\mathrm{d}\theta\nonumber\\ &\qquad+\int_{0}^{1}
\mathrm{d}z \left[\varOmega(z, \theta) P_1- \frac{\partial
P_1}{\partial \theta}\right]_0^{2{\rm \pi}} =0.
\end{align}
It follows that the convective term then averages to zero in an appropriate sense, as demonstrated in the next subsection. In other words, the effective behaviour of ![]() $P_0$ is that of pure diffusion. Explicitly, with the normalisation condition, we obtain the drift as
$P_0$ is that of pure diffusion. Explicitly, with the normalisation condition, we obtain the drift as
An a posteriori solution for ![]() $P_1$ is available with the centring condition as
$P_1$ is available with the centring condition as
wherein ![]() $b(z,\theta )$ is governed by
$b(z,\theta )$ is governed by
 \begin{equation} \left. \begin{gathered}
\mathcal{L}b=P_{0}^{\infty }\left(
{{{Pe}}_{f}}U+{{{Pe}}_{s}}\sin
\theta -{{{\bar{U}}}} \right)-2{{D}_{xz}}\frac{\partial P_{0}^{\infty }}{\partial z},\\
\left.b\right|_{\theta=\theta_0} =\left.b
\right|_{\theta={\rm \pi}-\theta_0}, \quad \text{at } z=0,1,\\
\left. \frac{\partial b}{\partial
z}\right|_{\theta=\theta_0} ={-}\left. \frac{\partial
b}{\partial z}\right|_{\theta={\rm \pi}-\theta_0},\quad \text{at
} z=0,1,\\
\left.b\right|_{\theta=0}=\left.b\right|_{\theta=2 {\rm \pi}},
\\ \left.\frac{\partial b}{\partial
\theta}\right|_{\theta=0}=\left.\frac{\partial b}{\partial
\theta}\right|_{\theta=2 {\rm \pi}}. \end{gathered} \right\}
\end{equation}
\begin{equation} \left. \begin{gathered}
\mathcal{L}b=P_{0}^{\infty }\left(
{{{Pe}}_{f}}U+{{{Pe}}_{s}}\sin
\theta -{{{\bar{U}}}} \right)-2{{D}_{xz}}\frac{\partial P_{0}^{\infty }}{\partial z},\\
\left.b\right|_{\theta=\theta_0} =\left.b
\right|_{\theta={\rm \pi}-\theta_0}, \quad \text{at } z=0,1,\\
\left. \frac{\partial b}{\partial
z}\right|_{\theta=\theta_0} ={-}\left. \frac{\partial
b}{\partial z}\right|_{\theta={\rm \pi}-\theta_0},\quad \text{at
} z=0,1,\\
\left.b\right|_{\theta=0}=\left.b\right|_{\theta=2 {\rm \pi}},
\\ \left.\frac{\partial b}{\partial
\theta}\right|_{\theta=0}=\left.\frac{\partial b}{\partial
\theta}\right|_{\theta=2 {\rm \pi}}. \end{gathered} \right\}
\end{equation}
The boundary conditions are similar to those of ![]() $P_{0}^{\infty }$. Note that
$P_{0}^{\infty }$. Note that ![]() $\mathcal {L} [P_{0}( z,\theta )f( \xi,\tau )]=0$, so the arbitrary function
$\mathcal {L} [P_{0}( z,\theta )f( \xi,\tau )]=0$, so the arbitrary function ![]() $f(\xi,\tau )$ does not indeed enter into the moment equations.
$f(\xi,\tau )$ does not indeed enter into the moment equations.
It is obvious from (3.9) that ![]() $P_0^\infty$ multiplied by an arbitrary constant constitutes a complementary solution of
$P_0^\infty$ multiplied by an arbitrary constant constitutes a complementary solution of ![]() $b$. Thus, we introduce a normalisation condition as
$b$. Thus, we introduce a normalisation condition as
We then devise a decomposition of ![]() $b$ as
$b$ as
where the constant ![]() $\bar {B}$ is the integration of
$\bar {B}$ is the integration of ![]() $b$ over the cross-section, representing the initial information of probability. Indeed, it is the gradient of
$b$ over the cross-section, representing the initial information of probability. Indeed, it is the gradient of ![]() $B$ that is unique rather than
$B$ that is unique rather than ![]() $B$ itself since it has an additive constant
$B$ itself since it has an additive constant ![]() $\bar {B}$, as shown in (3.19). Nevertheless, only
$\bar {B}$, as shown in (3.19). Nevertheless, only ![]() $\boldsymbol {\nabla } B$, or alternatively
$\boldsymbol {\nabla } B$, or alternatively ![]() $b_N$ with the normalisation condition (Hill & Bees Reference Hill and Bees2002; Manela & Frankel Reference Manela and Frankel2003), other than
$b_N$ with the normalisation condition (Hill & Bees Reference Hill and Bees2002; Manela & Frankel Reference Manela and Frankel2003), other than ![]() $B$ enters into the computation of dispersivity. Solutions of long-time phenomenological transport coefficients can be derived with
$B$ enters into the computation of dispersivity. Solutions of long-time phenomenological transport coefficients can be derived with ![]() $b_N$ solely. Likewise, we will pursue a Galerkin solution of
$b_N$ solely. Likewise, we will pursue a Galerkin solution of ![]() $b_N$ as performed to
$b_N$ as performed to ![]() $P_0^\infty$. The difference lies in that the right-hand side becomes an inhomogeneous source term.
$P_0^\infty$. The difference lies in that the right-hand side becomes an inhomogeneous source term.
Next of interest to us is utilising ![]() $b$, which contains complete local information, to determine the analytical solution of the dispersivity directly.
$b$, which contains complete local information, to determine the analytical solution of the dispersivity directly.
3.4. Perturbations of second order
With the reflective and periodic boundary conditions, we have
 \begin{align} \left\langle \mathcal{L} P_2 \right\rangle &=\left\langle -\left[ {{Pe}}_f U_f(z)+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right]\frac{\partial {{P}_{1}}}{\partial \xi }+{{D}_{xx}}(\theta )\frac{{{\partial }^{2}}{{P}_{0}}}{\partial {{\xi }^{2}}} +2{{D}_{xz}}(\theta )\frac{{{\partial }^{2}}{{P}_{1}}}{\partial \xi \partial z}-\frac{\partial {{P}_{0}}}{\partial \tau } \right\rangle \nonumber\\ &= \left\langle {{Pe}}_s \cos \theta \frac{\partial P_2}{\partial z} +\frac{\partial \left[ \varOmega(z, \theta) P_2 \right]}{\partial \theta} -D_{xz}(\theta)\frac{\partial^2 P_1}{\partial \xi \partial z} -D_{zz}(\theta)\frac{\partial^2 P_2}{\partial z^2} -\frac{\partial^2 P_2}{\partial \theta^2} \right\rangle\nonumber\\ &={-}\int_{0}^{1} \,\mathrm{d}z \int_{0}^{2{\rm \pi}} \frac{\partial}{\partial z} \left[2D_{xz}(\theta)\frac{\partial P_1}{\partial \xi} +D_{zz}(\theta)\frac{\partial P_2}{\partial z}-{{Pe}}_s \cos \theta P_2 \right] \mathrm{d}\theta\nonumber\\ &\quad +\int_{0}^{1} \,\mathrm{d}z \left[\varOmega(z, \theta) P_2- \frac{\partial P_2}{\partial \theta}\right]_0^{2{\rm \pi}} =0. \end{align}
\begin{align} \left\langle \mathcal{L} P_2 \right\rangle &=\left\langle -\left[ {{Pe}}_f U_f(z)+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right]\frac{\partial {{P}_{1}}}{\partial \xi }+{{D}_{xx}}(\theta )\frac{{{\partial }^{2}}{{P}_{0}}}{\partial {{\xi }^{2}}} +2{{D}_{xz}}(\theta )\frac{{{\partial }^{2}}{{P}_{1}}}{\partial \xi \partial z}-\frac{\partial {{P}_{0}}}{\partial \tau } \right\rangle \nonumber\\ &= \left\langle {{Pe}}_s \cos \theta \frac{\partial P_2}{\partial z} +\frac{\partial \left[ \varOmega(z, \theta) P_2 \right]}{\partial \theta} -D_{xz}(\theta)\frac{\partial^2 P_1}{\partial \xi \partial z} -D_{zz}(\theta)\frac{\partial^2 P_2}{\partial z^2} -\frac{\partial^2 P_2}{\partial \theta^2} \right\rangle\nonumber\\ &={-}\int_{0}^{1} \,\mathrm{d}z \int_{0}^{2{\rm \pi}} \frac{\partial}{\partial z} \left[2D_{xz}(\theta)\frac{\partial P_1}{\partial \xi} +D_{zz}(\theta)\frac{\partial P_2}{\partial z}-{{Pe}}_s \cos \theta P_2 \right] \mathrm{d}\theta\nonumber\\ &\quad +\int_{0}^{1} \,\mathrm{d}z \left[\varOmega(z, \theta) P_2- \frac{\partial P_2}{\partial \theta}\right]_0^{2{\rm \pi}} =0. \end{align}
For the equation of the order of ![]() $\epsilon ^2$, substitution of solutions of
$\epsilon ^2$, substitution of solutions of ![]() $P_0$ (3.8) and
$P_0$ (3.8) and ![]() $P_1$ (3.16) into (3.7) gives
$P_1$ (3.16) into (3.7) gives
 $$\begin{gather} \mathcal{L}{{P}_{2}}=\left( P{{e}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right)b\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-\left( P{{e}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right) P_{0}^{\infty }\left( z,\theta \right)\frac{\partial f}{\partial \xi } \nonumber\\ +\,{{D}_{xx}}P_{0}^{\infty }\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-P_{0}^{\infty }\frac{\partial c}{\partial \tau }-2{{D}_{xz}}\frac{\partial b}{\partial z}\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}+2{{D}_{xz}}\frac{\partial P_{0}^{\infty }}{\partial z}\frac{\partial f}{\partial \xi }. \end{gather}$$
$$\begin{gather} \mathcal{L}{{P}_{2}}=\left( P{{e}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right)b\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-\left( P{{e}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right) P_{0}^{\infty }\left( z,\theta \right)\frac{\partial f}{\partial \xi } \nonumber\\ +\,{{D}_{xx}}P_{0}^{\infty }\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-P_{0}^{\infty }\frac{\partial c}{\partial \tau }-2{{D}_{xz}}\frac{\partial b}{\partial z}\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}+2{{D}_{xz}}\frac{\partial P_{0}^{\infty }}{\partial z}\frac{\partial f}{\partial \xi }. \end{gather}$$With (3.7) and (3.20), we obtain a second centring condition
 $$\begin{gather} \left\langle \left( {{{{Pe}}}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right) b\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-\left( {{{{Pe}}}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right) P_{0}^{\infty }\frac{\partial f}{\partial \xi } \right. \nonumber\\ \left. \qquad +\,{{D}_{xx}}P_{0}^{\infty }\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-P_{0}^{\infty }\frac{\partial c}{\partial \tau }-2{{D}_{xz}}\frac{\partial b}{\partial z}\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}+2{{D}_{xz}}\frac{\partial P_{0}^{\infty }}{\partial z}\frac{\partial f}{\partial \xi } \right\rangle =0. \end{gather}$$
$$\begin{gather} \left\langle \left( {{{{Pe}}}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right) b\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-\left( {{{{Pe}}}_{f}}U_f+{{{{Pe}}}_{s}}\sin \theta -{{{\bar{U}}}} \right) P_{0}^{\infty }\frac{\partial f}{\partial \xi } \right. \nonumber\\ \left. \qquad +\,{{D}_{xx}}P_{0}^{\infty }\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}-P_{0}^{\infty }\frac{\partial c}{\partial \tau }-2{{D}_{xz}}\frac{\partial b}{\partial z}\frac{{{\partial }^{2}}c}{\partial {{\xi }^{2}}}+2{{D}_{xz}}\frac{\partial P_{0}^{\infty }}{\partial z}\frac{\partial f}{\partial \xi } \right\rangle =0. \end{gather}$$
It could be seen from (3.16) that ![]() $f(\xi,\tau )$ does not contribute to
$f(\xi,\tau )$ does not contribute to ![]() $P_2$ with the help of the first centring condition (3.14). That is, the governing equation of the undetermined function
$P_2$ with the help of the first centring condition (3.14). That is, the governing equation of the undetermined function ![]() $c(\xi,\tau )$ is
$c(\xi,\tau )$ is
Note that the normalisation condition of ![]() $P_0$ has been utilised in (3.23). As the notation suggests, the migration of micro-swimmers subject to anisotropic diffusion in a confined channel is governed by an effective dispersion equation with the convective term averaged out. It implies evidently that the dispersivity reads
$P_0$ has been utilised in (3.23). As the notation suggests, the migration of micro-swimmers subject to anisotropic diffusion in a confined channel is governed by an effective dispersion equation with the convective term averaged out. It implies evidently that the dispersivity reads
Consequently, the enhanced diffusivity scales with the swim and flow Péclet numbers, and the molecular diffusivity is modified with an addition of the anisotropic effect. For ![]() $0 < \epsilon \ll 1$ and long times, the solution
$0 < \epsilon \ll 1$ and long times, the solution ![]() $P^\epsilon$ of (3.3) is approximated by
$P^\epsilon$ of (3.3) is approximated by ![]() $P_0$, a solution of the convection–diffusion equation with slowly varying initial conditions
$P_0$, a solution of the convection–diffusion equation with slowly varying initial conditions
The important point is that the parabolic equations, cf. (3.9) and (3.17), exhibit independence from the small-scale ![]() $\epsilon$. In certain cases, explicit solutions for the two partial differential equations are attainable, as will be shown in § 4.1. Even when this is not the case, the equations lend themselves to rigorous analysis or efficient numerical simulations. Due to the slowly varying coefficients, this is far less computationally expensive than the direct numerical simulation of (2.1). Specifically, (3.15) represents the mean drift velocity of an active Brownian particle, and (3.24) is the dispersivity as a sum of the convective Taylor contribution and the molecular contribution. In summary, the asymptotic phenomenological coefficients are derived precisely with a homogenisation method.
$\epsilon$. In certain cases, explicit solutions for the two partial differential equations are attainable, as will be shown in § 4.1. Even when this is not the case, the equations lend themselves to rigorous analysis or efficient numerical simulations. Due to the slowly varying coefficients, this is far less computationally expensive than the direct numerical simulation of (2.1). Specifically, (3.15) represents the mean drift velocity of an active Brownian particle, and (3.24) is the dispersivity as a sum of the convective Taylor contribution and the molecular contribution. In summary, the asymptotic phenomenological coefficients are derived precisely with a homogenisation method.
Orientation distribution could be obtained by the averaged zeroth moment over the lateral cross-section as ![]() $C^\theta =\int _{0}^{1} P_0^{\infty } (z, \theta )\, \mathrm {d}z$. The vertical flux is the product of normalised vertical polarisation
$C^\theta =\int _{0}^{1} P_0^{\infty } (z, \theta )\, \mathrm {d}z$. The vertical flux is the product of normalised vertical polarisation ![]() $C^z= \int _{0}^{2{\rm \pi} } P_0^{\infty } (z, \theta ) \,\mathrm {d} \theta$ and vertical concentration
$C^z= \int _{0}^{2{\rm \pi} } P_0^{\infty } (z, \theta ) \,\mathrm {d} \theta$ and vertical concentration ![]() $P^z= \int _{0}^{2{\rm \pi} } P_0^{\infty } \cos (\theta )(z, \theta )\, \mathrm {d} \theta / C^z$, with swim Péclet numbers as a coefficient, as
$P^z= \int _{0}^{2{\rm \pi} } P_0^{\infty } \cos (\theta )(z, \theta )\, \mathrm {d} \theta / C^z$, with swim Péclet numbers as a coefficient, as
Integrating (3.5) from ![]() $0$ to
$0$ to ![]() $1$ with respect to
$1$ with respect to ![]() $\theta$ gives
$\theta$ gives
That is, the vertical concentration is governed by the balance between lateral diffusion and convection. Hence, the ensemble-averaged effective vertical migration could be quantified by the ratio of vertical flux to vertical concentration, i.e. normalised vertical polarisation, as
For further research interest, the transient evolution of these transport coefficients can feature the temporal process in the anisotropic diffusion of active ellipsoids long before the Taylor dispersion regime (Guan et al. Reference Guan, Zeng, Li, Guo, Wu and Wang2021; Debnath et al. Reference Debnath, Jiang, Guan and Chen2022; Wang, Jiang & Chen Reference Wang, Jiang and Chen2022a, Reference Wang, Jiang and Chen2023). To reflect the transient evolution of ![]() $\bar {U}$ and
$\bar {U}$ and ![]() $\bar {D}$, we denote the transient drift velocity and dispersivity as
$\bar {D}$, we denote the transient drift velocity and dispersivity as ![]() $U_x(t)$ and
$U_x(t)$ and ![]() $D_T(t)$, respectively. Note that we should not take it for granted to write the streamwise drift velocity and dispersivity (Yasuda Reference Yasuda1984; Guan et al. Reference Guan, Zeng, Jiang, Guo, Wang, Wu, Li and Chen2022; Guan & Chen Reference Guan and Chen2024), by reducing the external integral of (3.15) and (3.24) directly. Instead, we should recover a streamwise definition from the time-dependent solutions of moments successively.
$D_T(t)$, respectively. Note that we should not take it for granted to write the streamwise drift velocity and dispersivity (Yasuda Reference Yasuda1984; Guan et al. Reference Guan, Zeng, Jiang, Guo, Wang, Wu, Li and Chen2022; Guan & Chen Reference Guan and Chen2024), by reducing the external integral of (3.15) and (3.24) directly. Instead, we should recover a streamwise definition from the time-dependent solutions of moments successively.
4. Migration of confined micro-swimmers
In this section, we will investigate the shear-induced migration of confined micro-swimmers subject to anisotropic diffusion in a Poiseuille flow
The external flow field exerts two effects on the transport processes: (a) streamwise convection leading to spatial non-uniformity; (b) shear-induced rotation causing orientational redistribution. This introduces inherently multi-scale effects for the evolution of the shear-induced migration of micro-swimmers.
4.1. Benchmark solutions without translational diffusion and particle shape anisotropy
First, we resort to a simple benchmark case of spheroidal (![]() $\alpha _0=0$) gyrotactic micro-swimmers without translational diffusion (
$\alpha _0=0$) gyrotactic micro-swimmers without translational diffusion (![]() $D_{\|}=D_\perp =0$). The steady distribution is
$D_{\|}=D_\perp =0$). The steady distribution is
With an a posteriori condition that the rotational diffusion results in a uniform angular distribution asymptotically, the governing equation of ![]() $P_0^\infty$ is independent of
$P_0^\infty$ is independent of ![]() $\theta$. In this way, (4.2) reduces to
$\theta$. In this way, (4.2) reduces to
Thus, an analytical solution is
Note that the benchmark solution (4.4) satisfies the reflective boundary conditions. We are aware that an identical formalism of this benchmark has also been proposed previously (Bearon et al. Reference Bearon, Hazel and Thorn2011; Vennamneni et al. Reference Vennamneni, Nambiar and Subramanian2020). For distributions of non-gyrotactic micro-swimmers (![]() $\lambda =0$), (4.4) asymptotes to uniformity as
$\lambda =0$), (4.4) asymptotes to uniformity as
Subsequently, the steady drift could be derived as
With the vertical migration velocity (3.29), it is interesting to see whether gyrotactic micro-swimmers tend to swim vertically within a horizontal flow in the presence of reorientation. The steady vertical polarisation equals zero asymptotically as
This may seem simple, but is in fact far reaching in that symmetric actuation leads to no ensemble-averaged vertical movement at a population level. Conversely, imposed symmetry breaking would bring some exceptional deviations from the prediction. That is, non-spherical shapes, external body forces and direct coupling effects in a noisy environment can all be exploited to generate effective locomotion of micro-swimmers.
4.2. Spatial patterns: effects of anisotropic diffusion at leading order
Gyrotaxis, which arises from the combined effects of gravity and shear, can induce an overall upward tendency of the micro-swimmers. Figure 2 illustrates the influence of anisotropic diffusion on steady distributions of the spatial and orientational probability. The exerted driving force is as weak as ![]() $\lambda = 0.5$, and the parallel translational diffusivity
$\lambda = 0.5$, and the parallel translational diffusivity ![]() $D_{\|}$ is tuned with
$D_{\|}$ is tuned with ![]() $D_{\perp }$ fixed as zero as a hallmark of anisotropy on the vertical diffusivity
$D_{\perp }$ fixed as zero as a hallmark of anisotropy on the vertical diffusivity ![]() $D_{zz}$, since the streamwise diffusivity and cross-diffusivity do not factor into
$D_{zz}$, since the streamwise diffusivity and cross-diffusivity do not factor into ![]() $P_0^\infty$. For strong translational diffusion, the concentration distribution approaches (yet will never reach) uniformity. Concurrently, the orientational distribution exhibits a preference for upward migration since gravity is sufficiently strong. In the limit of weak translational diffusion, the orientational distribution becomes fairly uniform while the concentration distribution shows peculiar accumulation at walls. With moderate diffusivity (
$P_0^\infty$. For strong translational diffusion, the concentration distribution approaches (yet will never reach) uniformity. Concurrently, the orientational distribution exhibits a preference for upward migration since gravity is sufficiently strong. In the limit of weak translational diffusion, the orientational distribution becomes fairly uniform while the concentration distribution shows peculiar accumulation at walls. With moderate diffusivity (![]() $10^{-5} \le D_{\|}\le 10^{-3}$), the concentration distribution exhibits wall accumulation due to gyrotaxis, as shown in figure 2(a). The peak of
$10^{-5} \le D_{\|}\le 10^{-3}$), the concentration distribution exhibits wall accumulation due to gyrotaxis, as shown in figure 2(a). The peak of ![]() $C^\theta$ occurs around
$C^\theta$ occurs around ![]() $3{\rm \pi} /2$ in figure 2(b), signifying a prevalence of upstream swimming. The amalgamation of these observations suggests that micro-swimmers rotate to swim against the flow near walls where the flow is relatively weak.
$3{\rm \pi} /2$ in figure 2(b), signifying a prevalence of upstream swimming. The amalgamation of these observations suggests that micro-swimmers rotate to swim against the flow near walls where the flow is relatively weak.

Figure 2. Steady distributions of concentration and orientation subject to gyrotaxis. Common parameters are ![]() ${{Pe}}_s=0.1$,
${{Pe}}_s=0.1$, ![]() ${{Pe}}_f=10$,
${{Pe}}_f=10$, ![]() $\alpha _0=0$,
$\alpha _0=0$, ![]() $\lambda =0.5$ and
$\lambda =0.5$ and ![]() $D_{\perp }=0$.
$D_{\perp }=0$.
Figure 3 illustrates an internal symmetry breaking originating from particle shape anisotropy, which in turn leads to the generation of steady non-zero vertical locomotion from the probability perspective. Using (2.3) with ![]() $\lambda =0$, the angular velocity of micro-swimmers is governed by the local flow vorticity and the shape-induced strain rate. For highly elongated particles (
$\lambda =0$, the angular velocity of micro-swimmers is governed by the local flow vorticity and the shape-induced strain rate. For highly elongated particles (![]() $\alpha _0=0.9$) swimming slowly (
$\alpha _0=0.9$) swimming slowly (![]() ${{Pe}}_s=0.1$) through the channel, it becomes evident that micro-swimmers tend to align themselves in a manner that amplifies effectively the impact of the strain rate, thereby sampling a position preferentially to compete against the pronounced fluid rotation. Specifically, the contribution of shape-induced rotation is maximally negative when the orientation angle
${{Pe}}_s=0.1$) through the channel, it becomes evident that micro-swimmers tend to align themselves in a manner that amplifies effectively the impact of the strain rate, thereby sampling a position preferentially to compete against the pronounced fluid rotation. Specifically, the contribution of shape-induced rotation is maximally negative when the orientation angle ![]() $\theta$ assumes values of either
$\theta$ assumes values of either ![]() ${\rm \pi} /2$ or
${\rm \pi} /2$ or ![]() $3{\rm \pi} /2$, in accordance with the orientation depicted in figure 3(b).
$3{\rm \pi} /2$, in accordance with the orientation depicted in figure 3(b).

Figure 3. Steady distributions of concentration and orientation subject to a shape-induced strain rate. Common parameters are ![]() ${{Pe}}_s=0.1$,
${{Pe}}_s=0.1$, ![]() ${{Pe}}_f=10$,
${{Pe}}_f=10$, ![]() $\alpha _0=1$ and
$\alpha _0=1$ and ![]() $\lambda =0$.
$\lambda =0$.
Various patterns of concentration and orientation distributions occur with different anisotropic diffusivities. We direct our attention to the influence of anisotropic diffusion in a comparably strong flow field (![]() ${{Pe}}_f=10$). In figure 3(a), for a large perpendicular diffusivity, swimmers tend to form a symmetric cup-like concentration focused around the centreline. Conversely, pairs of depletion layers emerge, displaced symmetrically about
${{Pe}}_f=10$). In figure 3(a), for a large perpendicular diffusivity, swimmers tend to form a symmetric cup-like concentration focused around the centreline. Conversely, pairs of depletion layers emerge, displaced symmetrically about ![]() $z=0.5$, with their maxima diminishing in amplitude while converging towards the wall as
$z=0.5$, with their maxima diminishing in amplitude while converging towards the wall as ![]() $D_{\perp }$ increases. A subtle transition from downstream to upstream swimming becomes noticeable in figure 3(b) from a probabilistic standpoint in response to stronger translational diffusion. In contrast to the gyrotactic cases discussed previously, the pronounced external flow reduces significantly the wall accumulation for elongated micro-swimmers. This effect arises from the rapid rotation imposed by the strong external flow on the particles near the wall, causing them to swim inward and compelling the elongated particles within the bulk to preferentially align themselves with the flow direction. The cup-like focusing pattern results from a delicate balance between shear alignment and diffusion. Thus a slight alteration in the diffusivity tensor can readily transition it into a bi-modal trapping pattern.
$D_{\perp }$ increases. A subtle transition from downstream to upstream swimming becomes noticeable in figure 3(b) from a probabilistic standpoint in response to stronger translational diffusion. In contrast to the gyrotactic cases discussed previously, the pronounced external flow reduces significantly the wall accumulation for elongated micro-swimmers. This effect arises from the rapid rotation imposed by the strong external flow on the particles near the wall, causing them to swim inward and compelling the elongated particles within the bulk to preferentially align themselves with the flow direction. The cup-like focusing pattern results from a delicate balance between shear alignment and diffusion. Thus a slight alteration in the diffusivity tensor can readily transition it into a bi-modal trapping pattern.
At finite translational diffusivities, we analyse the effect of strong isotropic diffusion with various ellipsoidal shapes and gyrotaxis strengths. In figure 4, the funnel-shaped concentration distribution is featured for non-gyrotactic elongated micro-swimmers. Recall that the perfectly spherical active particles would sample a uniform distribution in the ![]() $z$-space and exhibit no net vertical polarisation. The more the ellipsoids are elongated, the more enhanced the non-uniformity becomes. Both ends of the funnel-shaped distributions in figure 4(a) are anticipated as a result of the polarisation. Since the polarisation distribution is anti-symmetric about
$z$-space and exhibit no net vertical polarisation. The more the ellipsoids are elongated, the more enhanced the non-uniformity becomes. Both ends of the funnel-shaped distributions in figure 4(a) are anticipated as a result of the polarisation. Since the polarisation distribution is anti-symmetric about ![]() $z=0.5$, we consider only the upper half-plane. Due to shear-induced migration, the ellipsoidal micro-swimmers near the centreline tend to migrate upwards, i.e. towards high-shear regions. When micro-swimmers approach the upper wall, the reflective condition turns the swimming direction opposite, as indicated in figure 4(b). This observation for the reflective boundary conditions deviates from the high-shear trapping, as reported by Bearon & Hazel (Reference Bearon and Hazel2015) with extreme wall accumulation for a Robin boundary condition and by Ezhilan & Saintillan (Reference Ezhilan and Saintillan2015) with singular cusped profiles for a periodic double-Poiseuille boundary condition. The nomenclature of high-shear trapping with regard to this typical kind of steady concentration distribution, once deemed suitable for delineating this phenomenon, now appears less appropriate. More precisely, this constitutes a distinctive transport process moulded by the interplay between shape- and shear-induced migration, under the reflective boundary conditions. For spherical gyrotactic particles subject to strong isotropic diffusion, the deviation of the concentration distributions from uniformity in figure 4(c) and upswimming behaviour in figure 4(d) are remarkable and significantly enhanced with the gyrotaxis strengths. It is interesting to investigate the balance between gyrotactic upswimming and self-propulsion. With small
$z=0.5$, we consider only the upper half-plane. Due to shear-induced migration, the ellipsoidal micro-swimmers near the centreline tend to migrate upwards, i.e. towards high-shear regions. When micro-swimmers approach the upper wall, the reflective condition turns the swimming direction opposite, as indicated in figure 4(b). This observation for the reflective boundary conditions deviates from the high-shear trapping, as reported by Bearon & Hazel (Reference Bearon and Hazel2015) with extreme wall accumulation for a Robin boundary condition and by Ezhilan & Saintillan (Reference Ezhilan and Saintillan2015) with singular cusped profiles for a periodic double-Poiseuille boundary condition. The nomenclature of high-shear trapping with regard to this typical kind of steady concentration distribution, once deemed suitable for delineating this phenomenon, now appears less appropriate. More precisely, this constitutes a distinctive transport process moulded by the interplay between shape- and shear-induced migration, under the reflective boundary conditions. For spherical gyrotactic particles subject to strong isotropic diffusion, the deviation of the concentration distributions from uniformity in figure 4(c) and upswimming behaviour in figure 4(d) are remarkable and significantly enhanced with the gyrotaxis strengths. It is interesting to investigate the balance between gyrotactic upswimming and self-propulsion. With small ![]() $\lambda$, we have shown in figure 2 that the orientational distribution peaks in the upward direction. The swimmers migrate upwards rapidly near the centreline while exhibiting almost no net vertical locomotion near the wall. As gyrotaxis grows, a steady concentration layer of micro-swimmers forms with appreciable thickness due to the wall reflection and shear trapping. The thickness of this accumulation layer declines rapidly when gyrotaxis or diffusion dominates self-propulsion.
$\lambda$, we have shown in figure 2 that the orientational distribution peaks in the upward direction. The swimmers migrate upwards rapidly near the centreline while exhibiting almost no net vertical locomotion near the wall. As gyrotaxis grows, a steady concentration layer of micro-swimmers forms with appreciable thickness due to the wall reflection and shear trapping. The thickness of this accumulation layer declines rapidly when gyrotaxis or diffusion dominates self-propulsion.

Figure 4. Steady distributions of concentration and vertical migration velocity with different particle shape anisotropies and gyrotaxis: (a) vertical concentration distribution and (b) polarisation distribution for non-gyrotactic micro-swimmers (![]() $\lambda =0$); (c) vertical concentration distribution and (d) polarisation distribution for spherical micro-swimmers (
$\lambda =0$); (c) vertical concentration distribution and (d) polarisation distribution for spherical micro-swimmers (![]() $\alpha _0=0$). Common parameters are
$\alpha _0=0$). Common parameters are ![]() ${{Pe}}_s=0.1$,
${{Pe}}_s=0.1$, ![]() ${{Pe}}_f=5$,
${{Pe}}_f=5$, ![]() $D_{\|}=10^{-2}$ and
$D_{\|}=10^{-2}$ and ![]() $D_{\perp }=10^{-2}$.
$D_{\perp }=10^{-2}$.
Using (3.5), the change of orientation originates from three parts: (a) relative strength of the lateral translational diffusivity to the rotational diffusivity, (b) angular velocity under the external effect of flow orientation and gravity field and (c) reflection when bouncing at walls. As illustrated in figure 5, the micro-swimmers exhibit three distinct equilibrium orientations. A possible first state could be peaking at approximately ![]() $3{\rm \pi} /2$, indicative of horizontal swimming against the prevailing flow; the second displays a pronounced tendency to sample inclined angles relative to the upright direction; the third orientation represents a transitional mode positioned between the above two states. When strong rotational diffusion dominates, the equilibrium balance is dominated by gyrotaxis and self-propulsion. Steady concentration layers emerge as a consequence of gyrotactic trapping when gyrotaxis exhibits relative weakness. Conversely, for sufficiently robust gravitational forces, micro-swimmers accumulate invariably towards the wall, disregarding the wall reflection, and align themselves with the upstream direction, as illustrated in figure 5(a,b). Note that the transition from low to high gyrotaxis signifies a distinct concentration distribution, in which a persistent characteristic peak becomes conspicuously pronounced, surpassing the nearby average values on both sides of the wall. This observation aligns with the upswimming behaviour depicted in figure 5(c), wherein the trapping layers correspond to the negligible vertical migration velocity in the wall regions, and wall accumulations correspond to the approach of the peak of polarisation distribution towards
$3{\rm \pi} /2$, indicative of horizontal swimming against the prevailing flow; the second displays a pronounced tendency to sample inclined angles relative to the upright direction; the third orientation represents a transitional mode positioned between the above two states. When strong rotational diffusion dominates, the equilibrium balance is dominated by gyrotaxis and self-propulsion. Steady concentration layers emerge as a consequence of gyrotactic trapping when gyrotaxis exhibits relative weakness. Conversely, for sufficiently robust gravitational forces, micro-swimmers accumulate invariably towards the wall, disregarding the wall reflection, and align themselves with the upstream direction, as illustrated in figure 5(a,b). Note that the transition from low to high gyrotaxis signifies a distinct concentration distribution, in which a persistent characteristic peak becomes conspicuously pronounced, surpassing the nearby average values on both sides of the wall. This observation aligns with the upswimming behaviour depicted in figure 5(c), wherein the trapping layers correspond to the negligible vertical migration velocity in the wall regions, and wall accumulations correspond to the approach of the peak of polarisation distribution towards ![]() $z=1$.
$z=1$.

Figure 5. Steady distributions with different translational diffusivities and gyrotaxis. Common parameters are ![]() ${{Pe}}_s=0.1$,
${{Pe}}_s=0.1$, ![]() ${{Pe}}_f=10$ and
${{Pe}}_f=10$ and ![]() $\alpha _0=0$.
$\alpha _0=0$.
The magnitude of anisotropic diffusion impacts the migration of micro-swimmers only through the alteration of ![]() $D_{zz}$. That is,
$D_{zz}$. That is, ![]() $D_{\|}$ is dominant for the upswimming mode of orientation, while
$D_{\|}$ is dominant for the upswimming mode of orientation, while ![]() $D_{\perp }$ becomes advantageous for the upstream swimming mode. For large gyrotaxis (
$D_{\perp }$ becomes advantageous for the upstream swimming mode. For large gyrotaxis (![]() $\lambda =10$), micro-swimmers accumulate remarkably near the wall while displaying a pronounced preference for alignment against the flow direction. In this case, the existence of parallel diffusivity works indeed as an amplifier of the overall vertical translational diffusivity, thereby smoothing the sharp accumulation near the wall. Under moderate gyrotaxis conditions (
$\lambda =10$), micro-swimmers accumulate remarkably near the wall while displaying a pronounced preference for alignment against the flow direction. In this case, the existence of parallel diffusivity works indeed as an amplifier of the overall vertical translational diffusivity, thereby smoothing the sharp accumulation near the wall. Under moderate gyrotaxis conditions (![]() $\lambda =5$), the balance mechanism becomes more intricate with the potential gyrotactic trapping or wall accumulation. Here, translational diffusion is governed primarily by
$\lambda =5$), the balance mechanism becomes more intricate with the potential gyrotactic trapping or wall accumulation. Here, translational diffusion is governed primarily by ![]() $D_{\|}$, and anisotropic diffusion emerges into effect when
$D_{\|}$, and anisotropic diffusion emerges into effect when ![]() $D_{\|} \neq D_{\perp }$. With an increase in the magnitude of the overall
$D_{\|} \neq D_{\perp }$. With an increase in the magnitude of the overall ![]() $D_{zz}$, the concentration distribution becomes more flattened, transitioning from wall accumulation to gyrotactic trapping if gyrotaxis is fixed. During the approach to uniformity, a transitional characteristic peak is observed within the range of moderate values for
$D_{zz}$, the concentration distribution becomes more flattened, transitioning from wall accumulation to gyrotactic trapping if gyrotaxis is fixed. During the approach to uniformity, a transitional characteristic peak is observed within the range of moderate values for ![]() $D_{zz}$, e.g. the red line for
$D_{zz}$, e.g. the red line for ![]() $10^{-3}< D_{zz}<10^{-2}$ in figure 5(a).
$10^{-3}< D_{zz}<10^{-2}$ in figure 5(a).
4.3. Diversity in concentration distributions: effects of flow convection and self-propulsion
Figure 6 shows the effect of flow strength on steady distributions of concentration and orientation with weak self-propulsion and isotropic translational diffusion. Diversity of steady concentration distributions is revealed as a result of different shear strengths in figure 6(a). When the flow speed is comparable to the swim speed, micro-swimmers exhibit a flattened nearly uniform distribution whereas tiny accumulations at the wall and slight focusing near the centreline are observed. As shown in figure 6(b), the orientation distributions with different flow Péclet numbers are qualitatively consistent, aligning preferentially with the flow direction either along the upstream or downstream direction. With weak ![]() ${{Pe}}_f$, this non-uniformity of orientation is impaired remarkably. Interestingly, the upstream tendency is sampled a bit more from the probability perspective, consistent with the mechanism of upstream rheotaxis for wall accumulations similar to figure 5.
${{Pe}}_f$, this non-uniformity of orientation is impaired remarkably. Interestingly, the upstream tendency is sampled a bit more from the probability perspective, consistent with the mechanism of upstream rheotaxis for wall accumulations similar to figure 5.

Figure 6. Steady distributions of concentration and orientation as functions of flow Péclet numbers. Common parameters are ![]() ${{Pe}}_s=0.1$,
${{Pe}}_s=0.1$, ![]() $D_{\|}=10^{-4}$,
$D_{\|}=10^{-4}$, ![]() $D_{\perp }=10^{-4}$,
$D_{\perp }=10^{-4}$, ![]() $\lambda =0$ and
$\lambda =0$ and ![]() $\alpha _0=0.9$.
$\alpha _0=0.9$.
When the flow strength grows, shear trapping appears as a peculiar phenomenon featuring symmetric depletion layers about the centreline. For periodic boundary conditions, Vennamneni et al. (Reference Vennamneni, Nambiar and Subramanian2020) have discussed intensively and rationalised the trapping phenomenon. In the present work, due to the imposed boundary conditions, trapping would be more complicated and we define three potential patterns as centreline focusing, wall accumulation and shear trapping. Note that the bi-modal distribution of depletion layers is a hallmark of shear trapping, trapped either in the low- or high-shear regions. Of interest for us to elucidate are distributions and mechanisms in this new system with effective boundary conditions. As demonstrated in figure 3(a), the shear-induced migration of elongated micro-swimmers could form a cup-shaped focus at the centre for strong translational diffusion. In contrast, funnel-shaped shear trapping with reduced wall accumulation is found for low translational diffusivities and great flow strengths. As illustrated in figure 6(a), the trapped depth converges towards the centreline with increasing flow Péclet number. That is, the strong flow rotates rapidly the particles with the largest shear rates at ![]() $z=0 \textrm { and } 1$, thereby depleting the near-wall micro-swimmers and rushing them inward. On the other hand, the micro-swimmers on the centreline migrate with an inclined angle to the flow direction, only stable when swimming away from the centreline since they would otherwise experience an anti-symmetric flow vorticity. Combining these two mechanisms, the bi-modal trapping distribution is formed. Note that the orientation still peaks around
$z=0 \textrm { and } 1$, thereby depleting the near-wall micro-swimmers and rushing them inward. On the other hand, the micro-swimmers on the centreline migrate with an inclined angle to the flow direction, only stable when swimming away from the centreline since they would otherwise experience an anti-symmetric flow vorticity. Combining these two mechanisms, the bi-modal trapping distribution is formed. Note that the orientation still peaks around ![]() ${\rm \pi} /2$ and
${\rm \pi} /2$ and ![]() $3{\rm \pi} /2$, exhibiting upstream rheotaxis and shear alignment in figure 6(b), whereas the width of the Gaussian-like distribution decreases with
$3{\rm \pi} /2$, exhibiting upstream rheotaxis and shear alignment in figure 6(b), whereas the width of the Gaussian-like distribution decreases with ![]() ${{Pe}}_f$.
${{Pe}}_f$.
Steady distributions of concentration and orientation for moderate values of ![]() ${{Pe}}_f$ as functions of swim Péclet numbers are presented in figure 7. With small
${{Pe}}_f$ as functions of swim Péclet numbers are presented in figure 7. With small ![]() ${{Pe}}_s$, the micro-swimmers become trapped near the central axis and walls, resulting in a symmetrical depletion layer around
${{Pe}}_s$, the micro-swimmers become trapped near the central axis and walls, resulting in a symmetrical depletion layer around ![]() $z=0.5$. Within the near-wall domains, a balance is achieved between stochastic swimming and wall reflection at a fixed depth, thereby trapping particles preferentially aligned with the flow. In the central region, the mechanism of shear-induced alignment contributes to various sampling modes of micro-swimmers. Note that the trapping depth converges towards the boundary plates as self-propulsion intensifies. As
$z=0.5$. Within the near-wall domains, a balance is achieved between stochastic swimming and wall reflection at a fixed depth, thereby trapping particles preferentially aligned with the flow. In the central region, the mechanism of shear-induced alignment contributes to various sampling modes of micro-swimmers. Note that the trapping depth converges towards the boundary plates as self-propulsion intensifies. As ![]() ${{Pe}}_s$ increases further, the trapping transitions into a pair of uni-modal distributions symmetric about
${{Pe}}_s$ increases further, the trapping transitions into a pair of uni-modal distributions symmetric about ![]() $z=0.5$. When self-propulsion is as strong as or even surpasses flow convection, noteworthy wall accumulations and subtle centreline focusing phenomena are observed. With increasing swim Péclet numbers, the characteristic alignment of ellipsoidal micro-swimmers is compressed considerably, resulting in a nearly uniform distribution in both the position and orientation spaces. That is, the strength of shear-induced trapping is influenced significantly by the swim Péclet numbers, with its highest manifestation occurring at intermediate levels of activity (Rusconi et al. Reference Rusconi, Guasto and Stocker2014). However, the active swimming could not alter qualitatively the steady distributions, yet eliminate quantitatively the deviations between the near-wall regions and the central area.
$z=0.5$. When self-propulsion is as strong as or even surpasses flow convection, noteworthy wall accumulations and subtle centreline focusing phenomena are observed. With increasing swim Péclet numbers, the characteristic alignment of ellipsoidal micro-swimmers is compressed considerably, resulting in a nearly uniform distribution in both the position and orientation spaces. That is, the strength of shear-induced trapping is influenced significantly by the swim Péclet numbers, with its highest manifestation occurring at intermediate levels of activity (Rusconi et al. Reference Rusconi, Guasto and Stocker2014). However, the active swimming could not alter qualitatively the steady distributions, yet eliminate quantitatively the deviations between the near-wall regions and the central area.

Figure 7. Steady distributions of concentration and orientation as functions of the swim Péclet numbers. Common parameters are ![]() ${{Pe}}_f=10$,
${{Pe}}_f=10$, ![]() $D_{\|}=10^{-4}$,
$D_{\|}=10^{-4}$, ![]() $D_{\perp }=10^{-4}$,
$D_{\perp }=10^{-4}$, ![]() $\lambda =0$ and
$\lambda =0$ and ![]() $\alpha _0=0.9$.
$\alpha _0=0.9$.
5. Transient solutions and evolution of phenomenological transport coefficients
To comprehend the transient impacts of anisotropic diffusion, we investigate the temporal evolution of typical phenomenological transport coefficients. Non-spherical shape anisotropy and external gravitational forces are employed to induce vertical locomotion at a population level. Specifically, coupled diffusivities are revealed to influence remarkably the transient drift velocity ![]() $U_x(t)$ and dispersivity
$U_x(t)$ and dispersivity ![]() $D_T(t)$ at high orders.
$D_T(t)$ at high orders.
Unlike spherical particles in a Poiseuille flow, elongated micro-swimmers display a persistent non-zero drift for asymptotically long times, as demonstrated in figure 8(a). Initially, the micro-swimmers are displaced on the centreline where flow convection is most pronounced, resulting in a notably positive drift relative to the mean flow speed. A sharp decline in transient drift is expected as micro-swimmers diffuse stochastically and swim actively, causing disparate sampling of individual streamlines with unequal probabilities over time. Consequently, this preferential sampling leads to a modest temporal increase in drift during the transitional phase. For the asymptotic dispersion period, the drift converges asymptotically to a constant value, as predicted by (3.15). In the scenario involving elongated micro-swimmers with robust self-propulsion, the upstream rheotaxis surpasses distinctly the flow convection for asymptotically long times, a trend that is augmented with higher cross-diffusivity ![]() $D_{xz}$. Utilising (3.15), it becomes apparent that the inclusion of a non-zero
$D_{xz}$. Utilising (3.15), it becomes apparent that the inclusion of a non-zero ![]() $D_{\|}$, corresponding to the isotropic condition in the present case, indeed magnifies the overall cross-diffusivity. A monotonic increase in the effective diffusivity, known as dispersivity, is observed due to the combined effects of swimming dispersion and shear dispersion. Specifically, anisotropic diffusion modifies dispersivity by means of streamwise diffusivity and cross-diffusivities. Figure 8(b) displays a notably increased diffusivity, by orders of magnitude, relative to the overall translational diffusivity. For the isotropic case, cross-diffusivities play no role in determining dispersivity; hence, effective diffusion is reinforced as overall streamwise diffusivity (
$D_{\|}$, corresponding to the isotropic condition in the present case, indeed magnifies the overall cross-diffusivity. A monotonic increase in the effective diffusivity, known as dispersivity, is observed due to the combined effects of swimming dispersion and shear dispersion. Specifically, anisotropic diffusion modifies dispersivity by means of streamwise diffusivity and cross-diffusivities. Figure 8(b) displays a notably increased diffusivity, by orders of magnitude, relative to the overall translational diffusivity. For the isotropic case, cross-diffusivities play no role in determining dispersivity; hence, effective diffusion is reinforced as overall streamwise diffusivity (![]() $D_{xx}$) increases. With the predominance of shear dispersion subject to anisotropic diffusion, an increase in
$D_{xx}$) increases. With the predominance of shear dispersion subject to anisotropic diffusion, an increase in ![]() $D_{\perp }$ leads to a reduction in dispersivity, which arises from the adverse influence of associated coupling terms.
$D_{\perp }$ leads to a reduction in dispersivity, which arises from the adverse influence of associated coupling terms.

Figure 8. Transient distributions of phenomenological transport coefficients. The swimmers are initially displaced at ![]() $z=0.5$ and uniformly oriented. Common parameters are
$z=0.5$ and uniformly oriented. Common parameters are ![]() ${{Pe}}_s=1$,
${{Pe}}_s=1$, ![]() ${{Pe}}_f=10$,
${{Pe}}_f=10$, ![]() $\alpha _0=0.9$ and
$\alpha _0=0.9$ and ![]() $\lambda =0$.
$\lambda =0$.
Finally, our focus shifts to gyrotactic micro-swimmers exposed to an external gravitational field, as shown in figure 9. For simplicity, we maintain the perpendicular diffusivity at zero and manipulate the parallel diffusivity to elucidate the influence of anisotropic diffusion. As evidenced previously in figure 2, gyrotactic micro-swimmers accumulate near the wall in the dispersion regime and exhibit a pronounced preference for upstream migration. Consequently, we anticipate that gyrotactic micro-swimmers will experience downstream convection with a positive drift as initially discharged at the centreline, later exhibit transient rises due to stochastic swimming and eventually converge to a constant negative value due to upstream rheotaxis. Upstream migration becomes more pronounced with increasing gyrotaxis, as shown in figure 9(a). Enhanced diffusion, exhibiting a monotonic time-dependent behaviour, is observed in comparison with the original translational diffusion, as depicted in figure 9(b). Notably, in the exceptional scenario of pronounced gyrotaxis (![]() $\lambda =5$) coupled with low translational diffusivities, a non-monotonic dependence of transient dispersivity on time and a significant reduction in asymptotic dispersivity are observed. This phenomenon arises because nearly all micro-swimmers accumulate near the wall regions where flow convection is minimal, resulting in limited opportunities for bulk streamline sampling through Brownian diffusion.
$\lambda =5$) coupled with low translational diffusivities, a non-monotonic dependence of transient dispersivity on time and a significant reduction in asymptotic dispersivity are observed. This phenomenon arises because nearly all micro-swimmers accumulate near the wall regions where flow convection is minimal, resulting in limited opportunities for bulk streamline sampling through Brownian diffusion.

Figure 9. Transient distributions of phenomenological transport coefficients under gravity. The swimmers are initially displaced at ![]() $z=0.5$ and uniformly oriented. Common parameters are
$z=0.5$ and uniformly oriented. Common parameters are ![]() ${{Pe}}_s=1$,
${{Pe}}_s=1$, ![]() ${{Pe}}_f=10$,
${{Pe}}_f=10$, ![]() $\alpha _0=0.9$,
$\alpha _0=0.9$, ![]() $D_{\perp }=0$ and
$D_{\perp }=0$ and ![]() $\lambda =0.5$ (unless otherwise declared).
$\lambda =0.5$ (unless otherwise declared).
6. Conclusion
This work establishes a population-level theoretical framework aimed at modelling macro-transport processes of elongated micro-swimmers involving anisotropic diffusion. In the absence of shape anisotropy and stochastic diffusion, we present a detailed examination of a benchmark solution of the zeroth moment for spheroidal gyrotactic micro-swimmers.
Utilising the analytical solutions, we demonstrate that symmetric actuation in a horizontal flow does not lead to net vertical locomotion of micro-swimmers from the probability perspective, unless non-spherical shapes, external fields or direct coupling effects are utilised to induce vertical polarisation. The inherent asymmetries and external fields can exert substantial influence on the observed concentration and orientation profiles of self-propelling micro-swimmers, as well as phenomenological transport coefficients.
Multiple patterns of shear-induced migration are elucidated with varying anisotropic diffusivities. In particular, highly elongated particles, moving slowly through a confined channel, tend to align themselves in a manner that amplifies the adverse effects of the strain rate, thereby adapting to balance the pronounced fluid rotation. It is intriguing to observe a distinct and persistent peak of the concentration distribution with moderate gyrotaxis, surpassing the nearby average values on both channel walls. Diverse collective behaviours encompassing upstream migration and shear alignment, as well as the formation of depletion layers, centreline focusing and surface accumulation, have been observed for various swim and flow Péclet numbers.
Notably, as the flow strength increases, distinctive phenomena of shear trapping are characterised by a rich array of symmetric depletion layers around the centreline. This implies that shear-induced migration exhibits a high degree of independence from the intricacies of the propulsion system and reorientation mechanisms. We also observe and explain the remarkable phenomenon whereby a reduction in the perpendicular diffusivity increases the effective diffusivity caused by the shear dispersion mechanism. A substantial decrease in steady dispersivity has been reported, deviating from the expectations of classical Taylor dispersion theory.
The theoretical analysis offers valuable insights into understanding distinct self-propulsion strategies and the transport dynamics within active-matter systems. As a first step, the current study has the potential to tackle a multitude of transport problems stemming from external or inter-particle interactions of spatially varying shapes, sizes and others for swimmers in constrained environments. For example, micro-swimmers can generate stress in the fluid, potentially causing collective motion at higher concentrations (Nordanger et al. Reference Nordanger, Morozov and Stenhammar2022). Jeffery orbits, typically associated with Newtonian fluids, undergo notable changes due to viscoelastic stresses induced by the activity (Choudhary, Nambiar & Stark Reference Choudhary, Nambiar and Stark2023). The conceptualisation of the rheological dynamics in dense active suspensions is absent from the present theoretical framework. Future work could encompass extensions to incorporate high-concentration interactions, non-Newtonian effects and realistic boundary conditions.
Acknowledgements
Valuable discussions with Bohan Wang, Li Zeng, Zi Wu and Zhi Li are appreciated.
Funding
This work is supported by the National Natural Science Foundation of China (grant numbers 123B2039, 12372379 and 52109093) and the Science and Technology Development Fund (FDCT) of Macao SAR (grant number 0018/2023/ITP1).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Time-dependent solutions
Following our previous analyses (Jiang & Chen Reference Jiang and Chen2020, Reference Jiang and Chen2021; Wang et al. Reference Wang, Jiang and Chen2022b; Guan et al. Reference Guan, Jiang, Wang, Zeng, Li and Chen2023), we can define the local moments as
The global moments, i.e. the moments of the averaged probability distribution function, are
The governing moment equation for micro-swimmers with anisotropic diffusion reads
with the understanding that ![]() $P_{-1}=P_{-2}=0$.
$P_{-1}=P_{-2}=0$.
Accordingly, a reflective boundary condition in the position space is imposed as
In the orientation space, periodic boundary conditions are
The initial condition is
Integration of (A3) with regard to ![]() $\theta$ and
$\theta$ and ![]() $z$ by use of reflective boundary conditions yields the governing equation of global moments
$z$ by use of reflective boundary conditions yields the governing equation of global moments ![]() $M_n$ as
$M_n$ as
Note that ![]() $M_0=1$. The initial conditions of global moments read
$M_0=1$. The initial conditions of global moments read
The transient drift velocity ![]() $U_x$ and dispersivity
$U_x$ and dispersivity ![]() $D_T$ can be calculated through moments as
$D_T$ can be calculated through moments as
where ![]() $\mu _x$ and
$\mu _x$ and ![]() $\sigma ^2$ are the mean displacement and mean square displacement calculated through moments, respectively, as
$\sigma ^2$ are the mean displacement and mean square displacement calculated through moments, respectively, as
The auxiliary eigenvalue problem concerning the governing equation of local moments (A3) is
wherein ![]() $\lambda _i$ represents the eigenvalue (
$\lambda _i$ represents the eigenvalue (![]() $i=1,2,\ldots$) and
$i=1,2,\ldots$) and ![]() $f_i$ the associated eigenfunction subject to the reflective boundary conditions. With the Galerkin method,
$f_i$ the associated eigenfunction subject to the reflective boundary conditions. With the Galerkin method, ![]() $\lambda _i$ and
$\lambda _i$ and ![]() $f_i$ can be solved (Jiang & Chen Reference Jiang and Chen2021; Guan et al. Reference Guan, Jiang, Wang, Zeng, Li and Chen2023). The eigenfunction
$f_i$ can be solved (Jiang & Chen Reference Jiang and Chen2021; Guan et al. Reference Guan, Jiang, Wang, Zeng, Li and Chen2023). The eigenfunction ![]() $f_i$ is
$f_i$ is
 \begin{equation} f_i = \sum_{j = 1}^{\infty} \phi_{i j} e_j, \end{equation}
\begin{equation} f_i = \sum_{j = 1}^{\infty} \phi_{i j} e_j, \end{equation}
where ![]() $\phi _{i j}$ denotes the coefficients of the expansion. In the present work, the basis function
$\phi _{i j}$ denotes the coefficients of the expansion. In the present work, the basis function ![]() $\{e_i\}_{i=1}^{\infty }$ comprises
$\{e_i\}_{i=1}^{\infty }$ comprises
 \begin{equation} \left. \begin{array}{@{}ll@{}} \dfrac{1}{\sqrt{2 {\rm \pi}}}, \quad \dfrac{1}{\sqrt{\rm \pi}} \cos (m \theta), & \dfrac{1}{\sqrt{\rm \pi}} \cos (n {\rm \pi}z),\\ \sqrt{\dfrac{2}{\rm \pi}} \cos (n {\rm \pi}z) \cos (m \theta), & \sqrt{\dfrac{2}{\rm \pi}} \sin (n {\rm \pi}z) \sin (m \theta). \end{array} \right\} \end{equation}
\begin{equation} \left. \begin{array}{@{}ll@{}} \dfrac{1}{\sqrt{2 {\rm \pi}}}, \quad \dfrac{1}{\sqrt{\rm \pi}} \cos (m \theta), & \dfrac{1}{\sqrt{\rm \pi}} \cos (n {\rm \pi}z),\\ \sqrt{\dfrac{2}{\rm \pi}} \cos (n {\rm \pi}z) \cos (m \theta), & \sqrt{\dfrac{2}{\rm \pi}} \sin (n {\rm \pi}z) \sin (m \theta). \end{array} \right\} \end{equation} Currently, the moment equation is not only related to the complicated local operator ![]() $\mathcal {L}$, but also carries extra cross-derivatives. Indeed, two challenges arise: (a) the existing analytical solutions are not suitable for the present configuration, and (b) the local operator associated with the reflective boundary conditions can be non-self-adjoint due to self-propulsion and rotation of active ellipsoids. The first difficulty requires extended solutions of the moment equations subject to anisotropic diffusion, extending the classical results from the separation of variables (Barton Reference Barton1983). The second difficulty could be resolved by constructing a set of functions satisfying the bi-orthogonality relation
$\mathcal {L}$, but also carries extra cross-derivatives. Indeed, two challenges arise: (a) the existing analytical solutions are not suitable for the present configuration, and (b) the local operator associated with the reflective boundary conditions can be non-self-adjoint due to self-propulsion and rotation of active ellipsoids. The first difficulty requires extended solutions of the moment equations subject to anisotropic diffusion, extending the classical results from the separation of variables (Barton Reference Barton1983). The second difficulty could be resolved by constructing a set of functions satisfying the bi-orthogonality relation
where ![]() $\delta _{ij}$ is the Kronecker delta, and
$\delta _{ij}$ is the Kronecker delta, and ![]() $f^{\star }_i$ is the dual basis function with respect to
$f^{\star }_i$ is the dual basis function with respect to ![]() $f_i$ corresponding to
$f_i$ corresponding to ![]() $\lambda _i$.
$\lambda _i$.
Appendix B. Monte Carlo simulation
Monte Carlo simulation is conducted to validate the analytical solutions of moments as well as macroscopic transport coefficients. The stochastic differential equations equivalent to the Smoluchowski equation of active particles in a Poiseuille flow read
wherein ![]() $\varOmega =-3{{Pe}}_f (2z-1) (1+\alpha _0 \cos 2\theta )$ in the Poiseuille flow. The infinitesimal generator of anisotropic diffusion is produced by independent Gaussian distributions with zero mean and variance of
$\varOmega =-3{{Pe}}_f (2z-1) (1+\alpha _0 \cos 2\theta )$ in the Poiseuille flow. The infinitesimal generator of anisotropic diffusion is produced by independent Gaussian distributions with zero mean and variance of ![]() $\mathrm {d}t$ at each time step.
$\mathrm {d}t$ at each time step.
The reflective boundary conditions are implemented as
A total number of ![]() $5\times 10^5$ particles are distributed reasonably according to the initial conditions of different cases to reach steady-state distributions of moments and macroscopic transport coefficients. To solve the stochastic differential equations, the Eulerian scheme with a non-dimensional time step of
$5\times 10^5$ particles are distributed reasonably according to the initial conditions of different cases to reach steady-state distributions of moments and macroscopic transport coefficients. To solve the stochastic differential equations, the Eulerian scheme with a non-dimensional time step of ![]() $\mathrm {d}t=10^{-4}$ is adopted to avoid multiple wall collisions within a single time step. The comparison of analytical results and numerical simulations is shown in figures 10 and 11, with excellent agreement.
$\mathrm {d}t=10^{-4}$ is adopted to avoid multiple wall collisions within a single time step. The comparison of analytical results and numerical simulations is shown in figures 10 and 11, with excellent agreement.