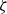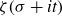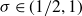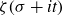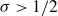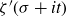1. Introduction
About fifty years ago, Sergey Voronin [Reference Voronin29]Footnote 1 proved his celebrated universality theorem for the Riemann zeta-function
![]() $\zeta(s)$
,
$\zeta(s)$
,
![]() $s=\sigma+it$
being a complex variable. This astonishing result states that, roughly speaking, certain shifts of the zeta-function approximate every zero-free analytic function, defined on a sufficiently small disk (see also [Reference Karatsuba and Voronin18]). In this paper we discuss a few new consequences of this remarkable property with respect to the curves given by the values of
$s=\sigma+it$
being a complex variable. This astonishing result states that, roughly speaking, certain shifts of the zeta-function approximate every zero-free analytic function, defined on a sufficiently small disk (see also [Reference Karatsuba and Voronin18]). In this paper we discuss a few new consequences of this remarkable property with respect to the curves given by the values of
![]() $\zeta(\sigma+it)$
as
$\zeta(\sigma+it)$
as
![]() $\sigma$
is fixed and t ranges through the set of real numbers or some subinterval. These curves look like spirals when t is from a bounded range, and we will use that word from time to time in what follows. The implications of universality that we consider here are by no means complicated in nature though they seem to have been overlooked so far.
$\sigma$
is fixed and t ranges through the set of real numbers or some subinterval. These curves look like spirals when t is from a bounded range, and we will use that word from time to time in what follows. The implications of universality that we consider here are by no means complicated in nature though they seem to have been overlooked so far.
For our purpose we recall the universality theorem [Reference Voronin29] in a stronger form: suppose that
![]() ${\mathcal K}$
is a compact subset of the strip
${\mathcal K}$
is a compact subset of the strip
![]() $1/2<{\rm{Re}}\,s<1$
with connected complement, and let g(s) be a non-vanishing continuous function on
$1/2<{\rm{Re}}\,s<1$
with connected complement, and let g(s) be a non-vanishing continuous function on
![]() ${\mathcal K}$
which is analytic in the interior of
${\mathcal K}$
which is analytic in the interior of
![]() ${\mathcal K}$
. Then, for every
${\mathcal K}$
. Then, for every
![]() $\epsilon>0$
,
$\epsilon>0$
,
(see [Reference Steuding26]). The main differences to Voronin’s original statement in [Reference Voronin29] are the positive lower density of the set of shifts
![]() $\tau$
(which is already implicit in Voronin’s proof) and the rather general set
$\tau$
(which is already implicit in Voronin’s proof) and the rather general set
![]() ${\mathcal K}$
where Voronin considered only disks; this is first apparent in Steve Gonek’s thesis [Reference Gonek10] and later in Bhaskar Bagchi’s thesis [Reference Bagchi2]. The topological restriction for
${\mathcal K}$
where Voronin considered only disks; this is first apparent in Steve Gonek’s thesis [Reference Gonek10] and later in Bhaskar Bagchi’s thesis [Reference Bagchi2]. The topological restriction for
![]() ${\mathcal K}$
follows from Mergelyan’s approximation theorem and its limitations (see [Reference Mergelyan21, Reference Steuding26, p. 107]). We will also make use of the following observation due to Johan Andersson [Reference Andersson1]: If
${\mathcal K}$
follows from Mergelyan’s approximation theorem and its limitations (see [Reference Mergelyan21, Reference Steuding26, p. 107]). We will also make use of the following observation due to Johan Andersson [Reference Andersson1]: If
![]() $\mathcal{K}$
has empty interior, then the target function g in the universality theorem is allowed to have zeros.
$\mathcal{K}$
has empty interior, then the target function g in the universality theorem is allowed to have zeros.
Assuming the Riemann Hypothesis, Gonek and Hugh Lowell Montgomery [Reference Gonek and Montgomery11] showed that the parametrised curve
![]() $t\mapsto \zeta(1/2+it)$
turns in the clockwise direction for all sufficiently large t or, in other words, the spiral has negative curvature (see Figure 1 for an illustration).Footnote 2 A simple application of the universality theorem shows that the behaviour to the right of the critical line can be rather different.
$t\mapsto \zeta(1/2+it)$
turns in the clockwise direction for all sufficiently large t or, in other words, the spiral has negative curvature (see Figure 1 for an illustration).Footnote 2 A simple application of the universality theorem shows that the behaviour to the right of the critical line can be rather different.

Fig 1. Left:
![]() $\zeta(1/2+it)$
for
$\zeta(1/2+it)$
for
![]() $0\leq t\leq 40$
; right:
$0\leq t\leq 40$
; right:
![]() $\zeta''/\zeta'(1/2+it)$
for the same range of t. The negative real part of
$\zeta''/\zeta'(1/2+it)$
for the same range of t. The negative real part of
![]() $\zeta''/\zeta'(1/2+it)$
for
$\zeta''/\zeta'(1/2+it)$
for
![]() $t\geq t_0=2.75\ldots$
corresponds to the clockwise direction of the spiral on the left.
$t\geq t_0=2.75\ldots$
corresponds to the clockwise direction of the spiral on the left.
For this purpose, we consider any parametrised curve
where
![]() ${\mathcal{I}}=[a,b]$
is an interval,
${\mathcal{I}}=[a,b]$
is an interval,
![]() $\sigma\in(1/2,1)$
is fixed. Then
$\sigma\in(1/2,1)$
is fixed. Then
![]() ${\mathcal K}=\{\sigma+it\,:\, t\in {\mathcal{I}}\}$
is a compact set in
${\mathcal K}=\{\sigma+it\,:\, t\in {\mathcal{I}}\}$
is a compact set in
![]() $1/2<{\rm{Re}}\,s<1$
with connected complement and empty interior. Hence, applying the universality theorem with
$1/2<{\rm{Re}}\,s<1$
with connected complement and empty interior. Hence, applying the universality theorem with
![]() $g(s)=\zeta(s)$
, implies the reappearance of the curve
$g(s)=\zeta(s)$
, implies the reappearance of the curve
![]() ${\mathcal C}$
within
${\mathcal C}$
within
![]() $\zeta(\sigma+i\mathbb{R})$
up to an invisible error of size
$\zeta(\sigma+i\mathbb{R})$
up to an invisible error of size
![]() $\epsilon$
on a set of positive lower density.
$\epsilon$
on a set of positive lower density.
However, we may also consider the inverse curve
This curve consists of the same points as
![]() ${\mathcal C}$
, only its direction is inverted. Thus, applying the universality theorem with
${\mathcal C}$
, only its direction is inverted. Thus, applying the universality theorem with
![]() $g(\sigma+it)=\zeta(\sigma+i(a+b-t))$
now yields the appearance of
$g(\sigma+it)=\zeta(\sigma+i(a+b-t))$
now yields the appearance of
![]() ${\mathcal C}^*$
within
${\mathcal C}^*$
within
![]() $\zeta(\sigma+i\mathbb{R})$
up to an invisible error of size
$\zeta(\sigma+i\mathbb{R})$
up to an invisible error of size
![]() $\epsilon$
for a set of positive lower density.
$\epsilon$
for a set of positive lower density.
We observe that the curvature of
![]() ${\mathcal C}^*$
is the negative of the curvature of
${\mathcal C}^*$
is the negative of the curvature of
![]() ${\mathcal C}$
. So the curvature of the parametrised curves
${\mathcal C}$
. So the curvature of the parametrised curves
![]() $t\mapsto \zeta(\sigma+it)$
for
$t\mapsto \zeta(\sigma+it)$
for
![]() $\sigma\in(1/2,1)$
takes both signs infinitely often as
$\sigma\in(1/2,1)$
takes both signs infinitely often as
![]() $t\to\infty$
, and both signs appear for a set of positive lower density. This is completely different to the situation on the critical line (if the Riemann Hypothesis is true).
$t\to\infty$
, and both signs appear for a set of positive lower density. This is completely different to the situation on the critical line (if the Riemann Hypothesis is true).
Note that the curvature changes its sign when t tends to
![]() $-\infty$
or
$-\infty$
or
![]() $\zeta(\sigma+it)$
is replaced by its conjugate
$\zeta(\sigma+it)$
is replaced by its conjugate
![]() $\zeta(\sigma-it)$
. But this change of orientation is of different nature as the reappearance of
$\zeta(\sigma-it)$
. But this change of orientation is of different nature as the reappearance of
![]() ${\mathcal C}^*$
in
${\mathcal C}^*$
in
![]() $\zeta(\sigma+i\mathbb{R})$
(up to a small error). The phenomenon in the background is, probably, an almost periodicity property of
$\zeta(\sigma+i\mathbb{R})$
(up to a small error). The phenomenon in the background is, probably, an almost periodicity property of
![]() $\zeta(\sigma+it)$
for
$\zeta(\sigma+it)$
for
![]() $\sigma>1/2$
in combination with universality. Computer experiments occasionally show an instance of a positive curvature in these spirals (see Figure 2).
$\sigma>1/2$
in combination with universality. Computer experiments occasionally show an instance of a positive curvature in these spirals (see Figure 2).

Fig 2. Left:
![]() $\zeta(3/4+it)$
for
$\zeta(3/4+it)$
for
![]() $110\leq t\leq 120$
; middle: the same for the range
$110\leq t\leq 120$
; middle: the same for the range
![]() $111.2\leq t\leq 111.7$
; right:
$111.2\leq t\leq 111.7$
; right:
![]() $\zeta''/\zeta'(3/4+it)$
for the same range of
$\zeta''/\zeta'(3/4+it)$
for the same range of
![]() $111.2\leq t\leq 111.7$
, where a positive real part indicates a positive curvature.
$111.2\leq t\leq 111.7$
, where a positive real part indicates a positive curvature.
2. Statement of the main results
In the sequel we assume every curve to be smooth, by which we mean that the plane and space curves under investigation have a parametrisation with at least second and third order continuous derivatives, respectively. We also assume that they are regular which means that their first derivative is non vanishing. We begin with a remarkable generalisation of the result from the introduction.
Theorem 1.
Let
![]() $\sigma\in(1/2,1)$
and
$\sigma\in(1/2,1)$
and
![]() $\epsilon>0$
be fixed. Then the following statements are true:
$\epsilon>0$
be fixed. Then the following statements are true:
-
(i) every plane curve is up to an error of size
 $O(\epsilon)$
and affine translation contained in the graph of the curve
$O(\epsilon)$
and affine translation contained in the graph of the curve
 $\mathbb{R}\ni t\mapsto\zeta(\sigma+it)\in\mathbb{C}$
;
$\mathbb{R}\ni t\mapsto\zeta(\sigma+it)\in\mathbb{C}$
; -
(ii) every space curve is encoded in the curve
 $\mathbb{R}\ni t\mapsto\zeta(\sigma+it)\in\mathbb{C}$
up to an error of size
$\mathbb{R}\ni t\mapsto\zeta(\sigma+it)\in\mathbb{C}$
up to an error of size
 $O(\epsilon)$
.
$O(\epsilon)$
.
Here, of course, we consider a plane curve in the euclidean plane via
![]() $\mathbb{R}^2\simeq \mathbb{C}$
also as a curve in the complex plane.
$\mathbb{R}^2\simeq \mathbb{C}$
also as a curve in the complex plane.
By the first statement of the theorem, the values of the zeta-function on any vertical line in the right open half of the critical strip provide an atlas for plane curves (similar as a normal number contains any finite pattern of digits).Footnote 3 A short note with this result and a sketch of its proof has appeared in [Reference Sourmelidis and Steuding25].

Fig 3. The spiral
![]() $\zeta(3/4+it)$
for
$\zeta(3/4+it)$
for
![]() $0\leq t\leq 35$
containing an approximation of a circle (in gray).
$0\leq t\leq 35$
containing an approximation of a circle (in gray).
The second statement relies on a simultaneous approximation of the curvature and the torsion of a space curve. The proof (in Section 3) is indeed an instance of a joint universality phenomenon for the real and the imaginary part of the zeta-function. Interestingly, the question whether the real and the imaginary part of the zeta-function can simultaneously approximate admissible target functions depends mainly on the set of definition of the target functions and can be answered positively and negatively:
Theorem 2.
The real and imaginary part of the zeta-function are jointly universal with respect to approximation of continuous real-valued functions defined on a compact set
![]() ${\mathcal K}\subseteq\lbrace s\in\mathbb{C}:1/2<{\rm Re}s<1\rbrace$
with connected complement if, and only if,
${\mathcal K}\subseteq\lbrace s\in\mathbb{C}:1/2<{\rm Re}s<1\rbrace$
with connected complement if, and only if,
![]() $\mathcal{K}$
has empty interior. More precisely, assume that
$\mathcal{K}$
has empty interior. More precisely, assume that
![]() $\mathcal{K}$
has empty interior and
$\mathcal{K}$
has empty interior and
![]() $f, g\,:\,{\mathcal K}\to\mathbb{R}$
are continuous. Then, for every sufficiently large T and every
$f, g\,:\,{\mathcal K}\to\mathbb{R}$
are continuous. Then, for every sufficiently large T and every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\tau\in[T,2T]$
such that
$\tau\in[T,2T]$
such that
moreover, the set of such
![]() $\tau$
has positive lower density. On the other hand, even if we assume any order of differentiability for f and g, the above statement can not be true if
$\tau$
has positive lower density. On the other hand, even if we assume any order of differentiability for f and g, the above statement can not be true if
![]() $\mathcal{K}$
contains an open disk.
$\mathcal{K}$
contains an open disk.
The positive statement of the above theorem shows that also curiosities as the Peano curve or other space-filling curves can be approximated as long as they have a continuous representation (see [Reference Sagan22]).
Motivated by the aforementioned result of Gonek and Montgomery about the clockwise direction of the spiral associated with the critical line we also consider the curves resulting from the values of the zeta-function on vertical line segments to the left of the critical line and to the right of the critical strip, respectively. It seems that the behaviour in the right open half of the critical strip is exceptional:
Theorem 3.
We consider the parametrised curve
![]() $t\mapsto \zeta(\sigma+it)$
for fixed
$t\mapsto \zeta(\sigma+it)$
for fixed
![]() $\sigma$
and any sufficiently large
$\sigma$
and any sufficiently large
![]() $t\geq t_0(\sigma)>0$
.
$t\geq t_0(\sigma)>0$
.
-
(i) There is a constant
 $A\in[3,4]$
such that the curvature is negative for
$A\in[3,4]$
such that the curvature is negative for
 $\sigma\geq A$
.
$\sigma\geq A$
. -
(ii) The curvature is negative for
 $\sigma\leq 0$
and under Riemann hypothesis also for
$\sigma\leq 0$
and under Riemann hypothesis also for
 $\sigma\leq 1/2$
.
$\sigma\leq 1/2$
. -
(iii) There exists
 $\theta>0$
such that the curvature has infinitely many sign changes for
$\theta>0$
such that the curvature has infinitely many sign changes for
 $\sigma\in(1/2,1+\theta)$
.
$\sigma\in(1/2,1+\theta)$
.
We will see below that the curvature of the curve
![]() $t\mapsto \zeta(\sigma+it)$
has the same sign as
$t\mapsto \zeta(\sigma+it)$
has the same sign as
Hence, to prove Theorem 3 it suffices to examine which sign does
![]() ${\rm{Re}}\, \zeta''/\zeta'(\sigma+it)$
take along vertical lines for various values of
${\rm{Re}}\, \zeta''/\zeta'(\sigma+it)$
take along vertical lines for various values of
![]() $\sigma\neq1/2$
. Although the last statement of Theorem 3 says that the curvature can be positive an infinitude of times for any
$\sigma\neq1/2$
. Although the last statement of Theorem 3 says that the curvature can be positive an infinitude of times for any
![]() $\sigma\in(1/2,1+\theta)$
, we will show that on average it is always negative. Indeed, we have the following
$\sigma\in(1/2,1+\theta)$
, we will show that on average it is always negative. Indeed, we have the following
Theorem 4.
For every
![]() $\sigma>1/2$
, the limit
$\sigma>1/2$
, the limit
exists and it represents an increasing and eventually constant function of
![]() $\sigma$
with maximum value
$\sigma$
with maximum value
![]() $-\log 2$
.
$-\log 2$
.
As a matter of fact, we will prove that the aforementioned limit at a point
![]() $\sigma$
is the derivative of the so-called Jensen function of
$\sigma$
is the derivative of the so-called Jensen function of
![]() $\zeta'$
, showing therefore a connection with the relative frequency of zeros of
$\zeta'$
, showing therefore a connection with the relative frequency of zeros of
![]() $\zeta'$
in the right of the vertical line
$\zeta'$
in the right of the vertical line
![]() $1/2+i\mathbb{R}$
.
$1/2+i\mathbb{R}$
.
Lastly, we consider a result of Ramūnas Garunkštis and the second author [Reference Garunkštis and Steuding9] who showed, under assumption of the Riemann Hypothesis, that
![]() $\zeta(\sigma+i\mathbb{R})$
is not dense in
$\zeta(\sigma+i\mathbb{R})$
is not dense in
![]() $\mathbb{C}$
for any fixed
$\mathbb{C}$
for any fixed
![]() $\sigma<1/2$
. Michel Lapidus [Reference Lapidus19] proved that also the converse is true; see also the recent book of Hafedh Herichi and Lapidus [Reference Herichi and Lapidus14]. We can strengthen these results slightly as follows:
$\sigma<1/2$
. Michel Lapidus [Reference Lapidus19] proved that also the converse is true; see also the recent book of Hafedh Herichi and Lapidus [Reference Herichi and Lapidus14]. We can strengthen these results slightly as follows:
Theorem 5.
The Riemann Hypothesis is true if, and only if,
![]() $\zeta(\sigma+i\mathbb{R})$
is nowhere dense in
$\zeta(\sigma+i\mathbb{R})$
is nowhere dense in
![]() $\mathbb{C}$
for any fixed
$\mathbb{C}$
for any fixed
![]() $\sigma<1/2$
.
$\sigma<1/2$
.
Harald Bohr and Richard Courant [Reference Bohr and Courant3] proved that
![]() $\zeta(\sigma+i\mathbb{R})$
is dense in
$\zeta(\sigma+i\mathbb{R})$
is dense in
![]() $\mathbb{C}$
for fixed
$\mathbb{C}$
for fixed
![]() $\sigma\in(1/2,1]$
. Of course, this result also follows from universality theorem (by choosing a constant target function). For the critical line, however, it is unknown whether
$\sigma\in(1/2,1]$
. Of course, this result also follows from universality theorem (by choosing a constant target function). For the critical line, however, it is unknown whether
![]() $\zeta(1/2+i\mathbb{R})$
dense in the complex plane or not. Universality does not apply to the critical line because of too many zeta zeros.
$\zeta(1/2+i\mathbb{R})$
dense in the complex plane or not. Universality does not apply to the critical line because of too many zeta zeros.
In the following four sections we give the proofs of these results. All our reasonings apply to more general zeta- and L-functions. What is necessary is a suitable universality theorem. Concerning the behaviour of the curvature and its sign changes to the right of the critical line, we conclude in Section 4 with the determination of the so-called Jensen function of
![]() $\zeta'$
(plus an appendix).
$\zeta'$
(plus an appendix).
3. Proof of Theorem 1
It is a well-known fact that a smooth plane curve is determined by its curvature. In fact, the fundamental theorem of the local theory of curves states that: given differentiable functions
![]() $\mathfrak{t},\kappa$
defined on an interval
$\mathfrak{t},\kappa$
defined on an interval
![]() ${\mathcal{I}}$
satisfying
${\mathcal{I}}$
satisfying
![]() $\kappa(t)>0$
for
$\kappa(t)>0$
for
![]() $t\in{\mathcal{I}}$
, there exists a regular parametrised curve
$t\in{\mathcal{I}}$
, there exists a regular parametrised curve
![]() $\gamma\,:\,{\mathcal{I}}\to \mathbb{R}^3$
such that t is the arclength (i.e. the euclidean norm of
$\gamma\,:\,{\mathcal{I}}\to \mathbb{R}^3$
such that t is the arclength (i.e. the euclidean norm of
![]() $\gamma'(t)$
equals 1 for every
$\gamma'(t)$
equals 1 for every
![]() $t\in\mathcal{I}$
),
$t\in\mathcal{I}$
),
![]() $\kappa(t)$
is the curvature, and
$\kappa(t)$
is the curvature, and
![]() $\mathfrak{t}(t)$
is the torsion of
$\mathfrak{t}(t)$
is the torsion of
![]() $\gamma$
. Moreover, any other curve
$\gamma$
. Moreover, any other curve
![]() $\tilde{\gamma}$
, satisfying the same conditions, differes from
$\tilde{\gamma}$
, satisfying the same conditions, differes from
![]() $\gamma$
by a rigid motion (meaning that there exists an orthogonal linear map
$\gamma$
by a rigid motion (meaning that there exists an orthogonal linear map
![]() $\ell$
and a vector v such that
$\ell$
and a vector v such that
![]() $\tilde{\gamma}=\ell\circ \gamma+v$
); see, for example, [Reference do Carmo5]. For plane curves there is no torsion, hence this result implies that a plane curve
$\tilde{\gamma}=\ell\circ \gamma+v$
); see, for example, [Reference do Carmo5]. For plane curves there is no torsion, hence this result implies that a plane curve
![]() $\gamma$
is indeed determined by its curvature; in this case, the curvature is not restricted to be positive. The proof relies on solving a system of certain differential equations, the so-called Frenet’s equations, and this plays also a certain role in the form of the integral equations (1) and (4) below.
$\gamma$
is indeed determined by its curvature; in this case, the curvature is not restricted to be positive. The proof relies on solving a system of certain differential equations, the so-called Frenet’s equations, and this plays also a certain role in the form of the integral equations (1) and (4) below.
We return to the first statement of Theorem 1. Let
![]() $\kappa$
be the curvature of a plane curve
$\kappa$
be the curvature of a plane curve
![]() ${\mathcal C}$
. Define
${\mathcal C}$
. Define
Then, a model of the curve
![]() ${\mathcal C}$
with curvature
${\mathcal C}$
with curvature
![]() $\kappa$
and arclength t in the complex plane is given by the parametrisation
$\kappa$
and arclength t in the complex plane is given by the parametrisation
where t ranges through some interval
![]() ${\mathcal{I}}$
. By the universality theorem, for every
${\mathcal{I}}$
. By the universality theorem, for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\tau>0$
such that
$\tau>0$
such that
In view of the positive lower density for the real shifts
![]() $\tau>0$
that lead to the desired approximation of the target function it follows that any plane curve appears infinitely often, up to a tiny error, in any curve
$\tau>0$
that lead to the desired approximation of the target function it follows that any plane curve appears infinitely often, up to a tiny error, in any curve
![]() $\zeta(\sigma+i\mathbb{R})$
with any fixed
$\zeta(\sigma+i\mathbb{R})$
with any fixed
![]() $\sigma\in(1/2,1)$
(even with positive lower density). In this sense, the zeta-function provides a single plane curve that contains all plane curves with an error too small to be seen with the naked eye!Footnote 4
$\sigma\in(1/2,1)$
(even with positive lower density). In this sense, the zeta-function provides a single plane curve that contains all plane curves with an error too small to be seen with the naked eye!Footnote 4
Next we consider space curves. If
![]() $c\,:\,{\mathcal{I}}\to\mathbb{R}^3$
is a parametrised curve with respect to its arclength t of curvature
$c\,:\,{\mathcal{I}}\to\mathbb{R}^3$
is a parametrised curve with respect to its arclength t of curvature
![]() $\kappa(t)>0$
and torsion
$\kappa(t)>0$
and torsion
![]() $\mathfrak{t}(t)$
, then the normal vector n(t) and binormal vector b(t) are given by
$\mathfrak{t}(t)$
, then the normal vector n(t) and binormal vector b(t) are given by
respectively (where
![]() $\times$
is the vector product). In this case the curve, defined by
$\times$
is the vector product). In this case the curve, defined by
is congruent to c up to some vector in
![]() $\mathbb{R}^3$
, because
$\mathbb{R}^3$
, because
![]() ${\tilde{c}}'(t)=c'(t)$
. Applying the universality theorem to the target function
${\tilde{c}}'(t)=c'(t)$
. Applying the universality theorem to the target function
![]() $t\mapsto \kappa(t)+i\mathfrak{t}(t)$
yields the desired approximation, where the quantities
$t\mapsto \kappa(t)+i\mathfrak{t}(t)$
yields the desired approximation, where the quantities
![]() $\kappa$
and
$\kappa$
and
![]() $\mathfrak{t}$
have in view of (3) and (4) to be replaced by
$\mathfrak{t}$
have in view of (3) and (4) to be replaced by
![]() ${\rm{Re}}\,\zeta(\sigma+it+i\tau)$
and
${\rm{Re}}\,\zeta(\sigma+it+i\tau)$
and
![]() ${\rm{Im}}\,\zeta(\sigma+it+i\tau)$
.
${\rm{Im}}\,\zeta(\sigma+it+i\tau)$
.
4. Proof of Theorem 2
We begin with the case of continuous real-valued functions f,g defined on a compact set with connected complement
![]() ${\mathcal K}\subseteq\lbrace s\in\mathbb{C}:1/2<\sigma<1\rbrace$
that has empty interior. For every sufficiently large T and every
${\mathcal K}\subseteq\lbrace s\in\mathbb{C}:1/2<\sigma<1\rbrace$
that has empty interior. For every sufficiently large T and every
![]() $\epsilon>0$
, by a direct application of the universality theorem, there exists
$\epsilon>0$
, by a direct application of the universality theorem, there exists
![]() $\tau\in[T,2T]$
such that
$\tau\in[T,2T]$
such that
Separating real and imaginary part, we thus have
Obviously, the set of such
![]() $\tau$
has positive lower density. This proves the first assertion of Theorem 2.
$\tau$
has positive lower density. This proves the first assertion of Theorem 2.
Next we consider the case where
![]() ${\mathcal K}$
has a non-empty interior or, equivalently, that it contains an open disk D. Assume that the real and imaginary part of the zeta-function do approximate two functions
${\mathcal K}$
has a non-empty interior or, equivalently, that it contains an open disk D. Assume that the real and imaginary part of the zeta-function do approximate two functions
![]() $f, g\,:\,{\mathcal K}\to\mathbb{R}$
in the sense of (5). Then we can find a sequence of real numbers
$f, g\,:\,{\mathcal K}\to\mathbb{R}$
in the sense of (5). Then we can find a sequence of real numbers
![]() $\tau_n>0$
with
$\tau_n>0$
with
The above implies that the sequence of analytic functions
![]() $\lbrace\zeta(s+i\tau_n)\rbrace_{n\geq1}$
converges uniformly in D to the function
$\lbrace\zeta(s+i\tau_n)\rbrace_{n\geq1}$
converges uniformly in D to the function
![]() $F(s):=f(s)+ig(s)$
. Hence, F(s) is analytic in D and, therefore, the partial derivatives of f and g as functions of two variables
$F(s):=f(s)+ig(s)$
. Hence, F(s) is analytic in D and, therefore, the partial derivatives of f and g as functions of two variables
![]() $(\sigma,t)$
exist and satisfy the Cauchy–Riemann equations in D. But this can be false in general if we choose a pair of functions f,g for which the Cauchy–Riemann equations fail.
$(\sigma,t)$
exist and satisfy the Cauchy–Riemann equations in D. But this can be false in general if we choose a pair of functions f,g for which the Cauchy–Riemann equations fail.
5. Proof of Theorem 3
Recall the aformenentioned result of Gonek and Montgomery [Reference Gonek and Montgomery11] who showed that the parametrised curve
![]() $t\mapsto \zeta(1/2+it)$
turns in the clockwise direction for all sufficiently large t. This follows from an older result due to Cem Yildirim [Reference Yildirim33] implying a negative curvature:
$t\mapsto \zeta(1/2+it)$
turns in the clockwise direction for all sufficiently large t. This follows from an older result due to Cem Yildirim [Reference Yildirim33] implying a negative curvature:
 \[\kappa(t)={{\rm{Re}}\, {\zeta''\over\zeta'}(1/2+it)\over \vert \zeta'(1/2+it)\vert}<0\qquad\mbox{for}\quad t\geq 2.76.\]
\[\kappa(t)={{\rm{Re}}\, {\zeta''\over\zeta'}(1/2+it)\over \vert \zeta'(1/2+it)\vert}<0\qquad\mbox{for}\quad t\geq 2.76.\]
Both results are conditional subject to the truth of the Riemann Hypothesis.
More generally, it can be seen, similarly as in [Reference Gonek and Montgomery11], that the curvature of the parametrised curve
![]() $t\mapsto \zeta(\sigma+it)$
is given by
$t\mapsto \zeta(\sigma+it)$
is given by
 \[\kappa(t)={{\rm{Re}}\, {\zeta''\over \zeta'}(\sigma+it)\over \vert\zeta'(\sigma+it)\vert},\]
\[\kappa(t)={{\rm{Re}}\, {\zeta''\over \zeta'}(\sigma+it)\over \vert\zeta'(\sigma+it)\vert},\]
whenever
![]() $\zeta'(\sigma+it)\neq 0$
. Thus, the sign of the curvature matches the one of
$\zeta'(\sigma+it)\neq 0$
. Thus, the sign of the curvature matches the one of
![]() $\mathrm{Re}\frac{\zeta''}{\zeta'} (\sigma+it)$
.
$\mathrm{Re}\frac{\zeta''}{\zeta'} (\sigma+it)$
.
From straightforward computations of the Dirichlet series expansion of
![]() $\zeta^{(k)}(s)$
,
$\zeta^{(k)}(s)$
,
![]() $k=1,2$
, it follows that there is a constant
$k=1,2$
, it follows that there is a constant
![]() $A\in[3,4]$
with
$A\in[3,4]$
with
Since
 \[{\rm{Re}}\, {\zeta''\over \zeta'}(s)=-\log 2\, \mathrm{Re}\frac{\frac{\zeta''(s)2^s}{(\log 2)^2}}{\frac{-\zeta'(s)2^s}{\log 2}},\]
\[{\rm{Re}}\, {\zeta''\over \zeta'}(s)=-\log 2\, \mathrm{Re}\frac{\frac{\zeta''(s)2^s}{(\log 2)^2}}{\frac{-\zeta'(s)2^s}{\log 2}},\]
we conclude from (6) that the curvature is negative for all
![]() $\sigma\geq A$
and the corresponding spirals turn in clockwise direction.
$\sigma\geq A$
and the corresponding spirals turn in clockwise direction.
In the half-plane
![]() $\sigma\leq0$
we can argue as Yildirim [Reference Yildirim33] did for
$\sigma\leq0$
we can argue as Yildirim [Reference Yildirim33] did for
![]() $0\leq\sigma\leq1/2$
. We start with the partial fraction representation
$0\leq\sigma\leq1/2$
. We start with the partial fraction representation
where
![]() $-a_n$
for
$-a_n$
for
![]() $n\geq1$
and
$n\geq1$
and
![]() $\rho_1:=\beta_1+i\gamma_1$
denote the real and non-real zeros of
$\rho_1:=\beta_1+i\gamma_1$
denote the real and non-real zeros of
![]() $\zeta'(s)$
, respectively. It is well known (see for example [Reference Levinson and Montgomery20, Theorem 9]) that
$\zeta'(s)$
, respectively. It is well known (see for example [Reference Levinson and Montgomery20, Theorem 9]) that
![]() $-a_n$
is the only zero of
$-a_n$
is the only zero of
![]() $\zeta'(s)$
in
$\zeta'(s)$
in
![]() $(-2n-2,-2n)$
and that there are no other zeros in the half-plane
$(-2n-2,-2n)$
and that there are no other zeros in the half-plane
![]() $\sigma\leq0$
.
$\sigma\leq0$
.
Taking the real parts on both sides of (7), we obtain
where the terms with
![]() $\rho_1$
and
$\rho_1$
and
![]() $\overline{\rho_1}$
are grouped together (observe that
$\overline{\rho_1}$
are grouped together (observe that
![]() $\zeta'(\overline{\rho_1})=0$
). Since
$\zeta'(\overline{\rho_1})=0$
). Since
![]() $\beta_1>0$
unconditionally, we have for any sufficiently large
$\beta_1>0$
unconditionally, we have for any sufficiently large
![]() $t>0$
that
$t>0$
that
 \begin{align*}{\rm Re}\frac{\zeta''}{\zeta'}(s)&=\frac{\zeta''}{\zeta'}(0)-2+\sum_{\rho_1}\frac{1}{\rho_1}+\sum_{\rho_1}\frac{\sigma-\beta_1}{(\sigma-\beta_1)^2+(t-\gamma_1)^2}-\sum_{n\geq1}\frac{a_n\sigma+|s|^2}{a_n|s+a_n|^2}\\&\leq\frac{\zeta''}{\zeta'}(0)-2+\sum_{\rho_1}\frac{1}{\rho_1}-\sum_{n\geq1}\frac{\sigma}{|s+a_n|^2}-\sum_{n\leq |s|}\frac{|s|^2}{a_n|s+a_n|^2}.\end{align*}
\begin{align*}{\rm Re}\frac{\zeta''}{\zeta'}(s)&=\frac{\zeta''}{\zeta'}(0)-2+\sum_{\rho_1}\frac{1}{\rho_1}+\sum_{\rho_1}\frac{\sigma-\beta_1}{(\sigma-\beta_1)^2+(t-\gamma_1)^2}-\sum_{n\geq1}\frac{a_n\sigma+|s|^2}{a_n|s+a_n|^2}\\&\leq\frac{\zeta''}{\zeta'}(0)-2+\sum_{\rho_1}\frac{1}{\rho_1}-\sum_{n\geq1}\frac{\sigma}{|s+a_n|^2}-\sum_{n\leq |s|}\frac{|s|^2}{a_n|s+a_n|^2}.\end{align*}
The first four terms on the right-hand side of the above relation are
![]() $O_\sigma(1)$
, while the last sum is of size approximately
$O_\sigma(1)$
, while the last sum is of size approximately
![]() $-\log t/2$
. Hence, the curve of
$-\log t/2$
. Hence, the curve of
![]() $\zeta(\sigma+it)$
turns in clockwise direction for any sufficiently large
$\zeta(\sigma+it)$
turns in clockwise direction for any sufficiently large
![]() $t>0$
. If we assume the Riemann hypothesis, then
$t>0$
. If we assume the Riemann hypothesis, then
![]() $\beta_1\geq1/2$
, as Andreas Speiser had proved [Reference Speiser24], and we also obtain Yildirim’s result in the left-half of the critical strip.
$\beta_1\geq1/2$
, as Andreas Speiser had proved [Reference Speiser24], and we also obtain Yildirim’s result in the left-half of the critical strip.
We have already seen in Theorem 1 that the curvature of
![]() $\zeta(\sigma+it)$
alternates its sign infinitely many times as
$\zeta(\sigma+it)$
alternates its sign infinitely many times as
![]() $t\to\infty$
for fixed
$t\to\infty$
for fixed
![]() $1/2<\sigma<1$
by an application of Voronin’s theorem. This can be extended to the vertical line
$1/2<\sigma<1$
by an application of Voronin’s theorem. This can be extended to the vertical line
![]() $\sigma=1$
by employing another variant of the universality theorem which is implicitly proved by Garunkštis et al. [Reference Garunkštis, Laurinčikas, Matsumoto, Steuding and Steuding8, Theorem 4]: Let
$\sigma=1$
by employing another variant of the universality theorem which is implicitly proved by Garunkštis et al. [Reference Garunkštis, Laurinčikas, Matsumoto, Steuding and Steuding8, Theorem 4]: Let
![]() $\sigma_0\in(1/2,1)$
,
$\sigma_0\in(1/2,1)$
,
![]() $r>0$
,
$r>0$
,
![]() $g:\mathcal{K}\to\mathbb{C}$
continuous,
$g:\mathcal{K}\to\mathbb{C}$
continuous,
![]() $g(s_0)\neq0$
and analytic for
$g(s_0)\neq0$
and analytic for
![]() $|s-s_0|<r$
. Then, for any
$|s-s_0|<r$
. Then, for any
![]() $\epsilon\in(0,|g(s_0)|)$
, there exist effectively computable positive numbers
$\epsilon\in(0,|g(s_0)|)$
, there exist effectively computable positive numbers
![]() $T_0$
and
$T_0$
and
![]() $\delta$
such that
$\delta$
such that
for any
![]() $\tau\in[T,2T]$
and
$\tau\in[T,2T]$
and
![]() $T\geq T_0$
. The proof does not depend on what
$T\geq T_0$
. The proof does not depend on what
![]() $\sigma_0$
may be, which works as a parameter therein, but rather what properties does the curve
$\sigma_0$
may be, which works as a parameter therein, but rather what properties does the curve
![]() $\zeta(\sigma_0+it)$
have. In particular, the basic ingredient in the proof of (8) is a weaker version of Voronin’s theorem, proved by Voronin [Reference Voronin30] himself: if
$\zeta(\sigma_0+it)$
have. In particular, the basic ingredient in the proof of (8) is a weaker version of Voronin’s theorem, proved by Voronin [Reference Voronin30] himself: if
![]() $\sigma_0\in(1/2,1)$
,
$\sigma_0\in(1/2,1)$
,
![]() $(a_1,a_2,\dots,a_N)$
is a vector of complex numbers and
$(a_1,a_2,\dots,a_N)$
is a vector of complex numbers and
![]() $\epsilon>0$
, then there exists an effectively computable positive number
$\epsilon>0$
, then there exists an effectively computable positive number
![]() $T_0$
such that
$T_0$
such that
for any
![]() $\tau\in[T,2T]$
and
$\tau\in[T,2T]$
and
![]() $T\geq T_0$
. However, if we are willing to drop effectivity and just accept the existence of infinitely many
$T\geq T_0$
. However, if we are willing to drop effectivity and just accept the existence of infinitely many
![]() $\tau>0$
satisfying the above inequalities, then
$\tau>0$
satisfying the above inequalities, then
![]() $\sigma_0=1$
is also admissible as Voronin [Reference Voronin28] had shown. Hence, it can be quickly confirmed that (8) holds also for
$\sigma_0=1$
is also admissible as Voronin [Reference Voronin28] had shown. Hence, it can be quickly confirmed that (8) holds also for
![]() $\sigma_0=1$
and a divergent sequence of
$\sigma_0=1$
and a divergent sequence of
![]() $\tau>0$
.
$\tau>0$
.
Assume now that
![]() $g(s)=e^s$
and
$g(s)=e^s$
and
![]() $\epsilon>0$
is sufficiently small. Then, it follows by (8) that there is some
$\epsilon>0$
is sufficiently small. Then, it follows by (8) that there is some
![]() $\delta_+\in(0,1)$
and a divergent sequence of
$\delta_+\in(0,1)$
and a divergent sequence of
![]() $\tau^+>0$
with
$\tau^+>0$
with
where the big O term is an analytic function in the interior of the disk. Therefore,
which implies that
Thus, the curvature of
![]() $\zeta(\sigma+it)$
is positive in disks of center
$\zeta(\sigma+it)$
is positive in disks of center
![]() $1+i\tau^+$
and radius
$1+i\tau^+$
and radius
![]() $\delta_+$
for a divergent sequence of real numbers
$\delta_+$
for a divergent sequence of real numbers
![]() $\tau^+>0$
. A similar argument with
$\tau^+>0$
. A similar argument with
![]() $g(s)=e^{-s}$
shows that the curvature of
$g(s)=e^{-s}$
shows that the curvature of
![]() $\zeta(\sigma+it)$
is negative in disks of center
$\zeta(\sigma+it)$
is negative in disks of center
![]() $1+i\tau^-$
and some radius
$1+i\tau^-$
and some radius
![]() $\delta_-$
for a divergent sequence of real numbers
$\delta_-$
for a divergent sequence of real numbers
![]() $\tau^->0$
. Hence, by taking
$\tau^->0$
. Hence, by taking
![]() $\theta=\min\lbrace\delta_+,\delta_-\rbrace$
, we conclude that there are infinitely many sign changes of the curvature on the vertical line
$\theta=\min\lbrace\delta_+,\delta_-\rbrace$
, we conclude that there are infinitely many sign changes of the curvature on the vertical line
![]() $1+i\mathbb{R}$
as well as in its immediate right neighbourhood.
$1+i\mathbb{R}$
as well as in its immediate right neighbourhood.
6. Proof of Theorem 4
We begin by setting the necessary theoretical background. Assume that f(s) is analytic, not identically zero and almost periodic in the sense of Bohr in a vertical strip
![]() $[\alpha,\beta]$
. Then, Børge Jessen [Reference Jessen15] has proved that the limit
$[\alpha,\beta]$
. Then, Børge Jessen [Reference Jessen15] has proved that the limit
exists uniformly in
![]() $[\alpha,\beta]$
and represents a continuous and convex function, which is known as the Jensen function of f. As a convex function,
$[\alpha,\beta]$
and represents a continuous and convex function, which is known as the Jensen function of f. As a convex function,
![]() $\phi_f(\sigma)$
is almost everywhere differentiable in the interval
$\phi_f(\sigma)$
is almost everywhere differentiable in the interval
![]() $[\alpha,\beta]$
and one can confirm that if
$[\alpha,\beta]$
and one can confirm that if
![]() $\alpha'\in(\alpha,\beta)$
is such a point, then
$\alpha'\in(\alpha,\beta)$
is such a point, then
This result was implicitly shown by Jessen [Reference Jessen15], Philip Hartman [Reference Hartman13], resp. Jessen and Hans Tornehave [Reference Jessen and Tornehave16]; we give a proof in the appendix.
In the context of Dirichlet series, Jessen and Tornehave [Reference Jessen and Tornehave16, Theorem 31] proved the following:
Theorem 1
(A). For an ordinary Dirichlet series
![]() $f(s)=\sum_{n\geq n_0}a_{n}n^{-s}$
,
$f(s)=\sum_{n\geq n_0}a_{n}n^{-s}$
,
![]() $a_{n_0}\neq0$
, with the uniform convergence abscissa
$a_{n_0}\neq0$
, with the uniform convergence abscissa
![]() $\alpha$
, the Jensen function
$\alpha$
, the Jensen function
![]() $\phi_f(\sigma)$
possesses in every half-plane
$\phi_f(\sigma)$
possesses in every half-plane
![]() $\sigma>\alpha_1>\alpha$
only a finite number of linearity intervals and a finite number of points of non-differentiability. If
$\sigma>\alpha_1>\alpha$
only a finite number of linearity intervals and a finite number of points of non-differentiability. If
![]() $\sigma_0$
denotes the supremum of the real parts of zeros of f(s) (which is always finite), then
$\sigma_0$
denotes the supremum of the real parts of zeros of f(s) (which is always finite), then
For an arbitrary strip
![]() $(\sigma_1,\sigma_2)$
where
$(\sigma_1,\sigma_2)$
where
![]() $\alpha<\sigma_1<\sigma_2<+\infty$
, the relative frequency of zeros
$\alpha<\sigma_1<\sigma_2<+\infty$
, the relative frequency of zeros
exists and it is determined by
This line of research has been pursued by Vibeke Borchsenius and Jessen [Reference Borchsenius and Jessen4, Theorem 1], in the case where f(s) can be analytically continued beyond its abscissa of uniform convergence. In particular, if
![]() $\phi_f(\sigma)$
and
$\phi_f(\sigma)$
and
![]() $H_f(\sigma_1,\sigma_2)$
are defined as above with the only difference that
$H_f(\sigma_1,\sigma_2)$
are defined as above with the only difference that
![]() $\gamma$
is a sufficiently large but fixed number and only
$\gamma$
is a sufficiently large but fixed number and only
![]() $\delta\to\infty$
, they proved the following:
$\delta\to\infty$
, they proved the following:
Theorem (B).
Let
![]() $-\infty\leq\alpha<\alpha_0<\beta_0<\beta\leq+\infty$
and
$-\infty\leq\alpha<\alpha_0<\beta_0<\beta\leq+\infty$
and
![]() $\gamma\in\mathbb{R}$
, and let
$\gamma\in\mathbb{R}$
, and let
![]() $f_1(s),f_2(s),\dots$
be a sequence of functions almost periodic in
$f_1(s),f_2(s),\dots$
be a sequence of functions almost periodic in
![]() $[\alpha,\beta]$
converging uniformly in
$[\alpha,\beta]$
converging uniformly in
![]() $[\alpha_0,\beta_0]$
towards a function f(s). Suppose, that none of the functions is identically zero. Suppose further, that f(s) may be continued analytically in the half-strip
$[\alpha_0,\beta_0]$
towards a function f(s). Suppose, that none of the functions is identically zero. Suppose further, that f(s) may be continued analytically in the half-strip
![]() $\alpha<\sigma<\beta$
,
$\alpha<\sigma<\beta$
,
![]() $t>\gamma$
, and that there is
$t>\gamma$
, and that there is
![]() $p>0$
such that
$p>0$
such that
for any reduced strip
![]() $\alpha<\alpha_1<\sigma<\beta_1<\beta$
. Then the Jensen function
$\alpha<\alpha_1<\sigma<\beta_1<\beta$
. Then the Jensen function
![]() $\phi_f(\sigma)$
exists in
$\phi_f(\sigma)$
exists in
![]() $[\alpha,\beta]$
and it is a continuous and convex function. If it is differentiable at
$[\alpha,\beta]$
and it is a continuous and convex function. If it is differentiable at
![]() $\sigma_1$
and
$\sigma_1$
and
![]() $\sigma_2$
for some
$\sigma_2$
for some
![]() $\alpha<\sigma_1<\sigma_2<\beta$
, then the relative frequency of zeros
$\alpha<\sigma_1<\sigma_2<\beta$
, then the relative frequency of zeros
![]() $H_f(\sigma_1,\sigma_2)$
exists and it is determined by
$H_f(\sigma_1,\sigma_2)$
exists and it is determined by
We note that (9) (with fixed
![]() $\gamma$
and
$\gamma$
and
![]() $\delta\to\infty$
) holds as well in points of the extended interval
$\delta\to\infty$
) holds as well in points of the extended interval
![]() $[\alpha,\beta]$
where
$[\alpha,\beta]$
where
![]() $\phi_f(\sigma)$
is differentiable.
$\phi_f(\sigma)$
is differentiable.
Next we apply the aforementioned results in the case of
![]() $f=\zeta'$
. Firstly, the derivative of the zeta-function can be represented as an absolutely convergent Dirichlet series in the half-plane
$f=\zeta'$
. Firstly, the derivative of the zeta-function can be represented as an absolutely convergent Dirichlet series in the half-plane
![]() $\sigma>1$
and it is zero-free in the half-plane
$\sigma>1$
and it is zero-free in the half-plane
![]() $\sigma>E$
for some
$\sigma>E$
for some
![]() $E\in[2,3]$
(see [Reference Titchmarsh27, Theorem 11·5 (C)]). Hence, in view of (9) and (10) we deduce that
$E\in[2,3]$
(see [Reference Titchmarsh27, Theorem 11·5 (C)]). Hence, in view of (9) and (10) we deduce that
For a positive integer n, let
![]() $\zeta^{\prime}_n(s):=\sum_{k\leq n}(-\log k)k^{-s}$
. Then, from the approximate functional equation for the Riemann zeta-function [Reference Titchmarsh27, Theorem 4·11], i.e.
$\zeta^{\prime}_n(s):=\sum_{k\leq n}(-\log k)k^{-s}$
. Then, from the approximate functional equation for the Riemann zeta-function [Reference Titchmarsh27, Theorem 4·11], i.e.
it follows that
for any reduced strip
![]() $1/2<\alpha_1<\sigma<\beta_1<3$
. Since the functions
$1/2<\alpha_1<\sigma<\beta_1<3$
. Since the functions
![]() $\zeta^{\prime}_n(s)$
for
$\zeta^{\prime}_n(s)$
for
![]() $n\geq1$
are almost periodic in any strip,
$n\geq1$
are almost periodic in any strip,
![]() $\phi_{\zeta'}(\sigma)$
exists in
$\phi_{\zeta'}(\sigma)$
exists in
![]() $(1/2,3)$
and, in addition, it is a continuous and convex function. As a matter of fact, it is also infinitely many times differentiable in this interval.
$(1/2,3)$
and, in addition, it is a continuous and convex function. As a matter of fact, it is also infinitely many times differentiable in this interval.
To see this, we observe that
The limit of the first term on the right-hand side is
![]() $\phi_\zeta(\sigma)$
and is equal to 0 for
$\phi_\zeta(\sigma)$
and is equal to 0 for
![]() $\sigma>1/2$
(see [Reference Borchsenius and Jessen4, Theorem 14, pages 162-163]). The limit of the second term on the right-hand side has been computed by Charng Rang Guo [Reference Guo12, Theorem 1·1·3] and it is equal to
$\sigma>1/2$
(see [Reference Borchsenius and Jessen4, Theorem 14, pages 162-163]). The limit of the second term on the right-hand side has been computed by Charng Rang Guo [Reference Guo12, Theorem 1·1·3] and it is equal to
where
![]() $\widehat{g}$
denotes the Fourier transform of a function g and
$\widehat{g}$
denotes the Fourier transform of a function g and
 \[{\chi}(x,y;\sigma):=\prod_p\int_0^1\exp\left(2\pi i\mathrm{Re}((x+iy)a(t,\sigma))\right)\mathrm{d}t,\quad a(t,\sigma):=\log p\sum_{m\geq1}\frac{\exp(2\pi imt)}{p^{m\sigma}}.\]
\[{\chi}(x,y;\sigma):=\prod_p\int_0^1\exp\left(2\pi i\mathrm{Re}((x+iy)a(t,\sigma))\right)\mathrm{d}t,\quad a(t,\sigma):=\log p\sum_{m\geq1}\frac{\exp(2\pi imt)}{p^{m\sigma}}.\]
Moreover, he showed that [Reference Guo12, Theorem 1·1·1]
![]() $G(\sigma)$
is infinitely many times differentiable in
$G(\sigma)$
is infinitely many times differentiable in
![]() $(1/2,3]$
with
$(1/2,3]$
with
In other words, Guo found the Jensen function of
![]() $\zeta'(s)$
and from his work and our previous discussion follows immediately that
$\zeta'(s)$
and from his work and our previous discussion follows immediately that
Moreover,
![]() $G'(\sigma)$
is increasing because
$G'(\sigma)$
is increasing because
![]() $G(\sigma)$
is a convex function. In combination with (11), we obtain the theorem.
$G(\sigma)$
is a convex function. In combination with (11), we obtain the theorem.
7. Proof of Theorem 5
For fixed
![]() $\sigma<1/2$
and
$\sigma<1/2$
and
![]() $\vert t\vert\geq 2$
, Garunkštis and Steuding [Reference Garunkštis and Steuding9] showed that
$\vert t\vert\geq 2$
, Garunkštis and Steuding [Reference Garunkštis and Steuding9] showed that
where
![]() $\epsilon>0$
is arbitrary and
$\epsilon>0$
is arbitrary and
![]() $c>0$
is an absolute constant depending only on
$c>0$
is an absolute constant depending only on
![]() $\epsilon$
and
$\epsilon$
and
![]() $\sigma$
. This lower bound relies on the conditional estimate
$\sigma$
. This lower bound relies on the conditional estimate
![]() $\zeta(\sigma+it)\gg \vert t\vert^{-\epsilon}$
for fixed
$\zeta(\sigma+it)\gg \vert t\vert^{-\epsilon}$
for fixed
![]() $\sigma>1/2$
(see [Reference Titchmarsh27, Section 14·2]) in combination with the functional equation. Since the right-hand side of (12) tends with
$\sigma>1/2$
(see [Reference Titchmarsh27, Section 14·2]) in combination with the functional equation. Since the right-hand side of (12) tends with
![]() $\vert t\vert$
to infinity, the curve
$\vert t\vert$
to infinity, the curve
![]() $t\mapsto \zeta(\sigma+it)$
spirals outside the disk of radius r centered at the origin for all sufficiently large values of
$t\mapsto \zeta(\sigma+it)$
spirals outside the disk of radius r centered at the origin for all sufficiently large values of
![]() $\vert t\vert$
. More precisely, if
$\vert t\vert$
. More precisely, if
![]() $\vert t\vert\geq r^{2/(1-2\sigma)}$
, then, for
$\vert t\vert\geq r^{2/(1-2\sigma)}$
, then, for
![]() $r\geq r_0$
, the values
$r\geq r_0$
, the values
![]() $\zeta(\sigma+it)$
lie in the complement of the disk. Therefore, it only remains to show that the image of the values
$\zeta(\sigma+it)$
lie in the complement of the disk. Therefore, it only remains to show that the image of the values
![]() $\zeta(\sigma+it)$
for t from a finite interval, [0,T] say, cannot be locally dense.
$\zeta(\sigma+it)$
for t from a finite interval, [0,T] say, cannot be locally dense.
Assume that the values
![]() $\zeta(\sigma+ it)$
are somewhere dense for
$\zeta(\sigma+ it)$
are somewhere dense for
![]() $t\in[0, T ]$
. Then there exists a small disk D such that the curve
$t\in[0, T ]$
. Then there exists a small disk D such that the curve
![]() $t \to \zeta(\sigma+it)$
visits for
$t \to \zeta(\sigma+it)$
visits for
![]() $t\in[0, T ]$
every tiny disk d of radius
$t\in[0, T ]$
every tiny disk d of radius
![]() $(3N)^{-1}$
centered at the elements of
$(3N)^{-1}$
centered at the elements of
![]() $\frac{1}{N} \mathbb{Z}[i]\cap D$
, where N is a large integer. Since the tiny disks d have distance
$\frac{1}{N} \mathbb{Z}[i]\cap D$
, where N is a large integer. Since the tiny disks d have distance
![]() $\gg N^{-1}$
one from another and there are
$\gg N^{-1}$
one from another and there are
![]() $\gg N^2$
many of them in D, the curve
$\gg N^2$
many of them in D, the curve
![]() $t \to\zeta(\sigma+it)$
has length
$t \to\zeta(\sigma+it)$
has length
![]() $\gg N^2\cdot N^{-1}=N$
which tends with N to infinity. This contradiction implies that the curve is nowhere dense.
$\gg N^2\cdot N^{-1}=N$
which tends with N to infinity. This contradiction implies that the curve is nowhere dense.
8. Appendix
If
then it follows from Jessen and Tornhave [Reference Jessen and Tornehave16, page 187] that
 \begin{eqnarray}\phi_f'(\sigma-0)& \leq& \mathop{\underline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma-0;\gamma,\delta)\nonumber\\&\leq & \left\{\begin{array}{l}\mathop{\overline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma-0;\gamma,\delta)\\\mathop{\underline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma+0;\gamma,\delta)\end{array}\right\}\\&\leq&\mathop{\overline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma+0;\gamma,\delta)\leq\phi_f'(\sigma+0).\nonumber\end{eqnarray}
\begin{eqnarray}\phi_f'(\sigma-0)& \leq& \mathop{\underline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma-0;\gamma,\delta)\nonumber\\&\leq & \left\{\begin{array}{l}\mathop{\overline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma-0;\gamma,\delta)\\\mathop{\underline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma+0;\gamma,\delta)\end{array}\right\}\\&\leq&\mathop{\overline{\lim}}_{(\delta-\gamma)\to\infty}\phi_f'(\sigma+0;\gamma,\delta)\leq\phi_f'(\sigma+0).\nonumber\end{eqnarray}
Therefore, if
![]() $\phi_f(\sigma)$
is differentiable at a point
$\phi_f(\sigma)$
is differentiable at a point
![]() $\sigma=\alpha'$
, then all of the above four limits are equal. In particular, we have
$\sigma=\alpha'$
, then all of the above four limits are equal. In particular, we have
as
![]() $\delta-\gamma\to\infty$
.
$\delta-\gamma\to\infty$
.
Now let
![]() $\gamma<\delta$
be a pair of real numbers. If f(s) has no zeros in the vertical segment
$\gamma<\delta$
be a pair of real numbers. If f(s) has no zeros in the vertical segment
![]() $[\alpha'+i\gamma,\alpha'+i\delta]$
, then it is analytic in a neighbourhood of this segment and, consequently,
$[\alpha'+i\gamma,\alpha'+i\delta]$
, then it is analytic in a neighbourhood of this segment and, consequently,
![]() $\phi_f(\sigma;\gamma,\delta)$
is differentiable at
$\phi_f(\sigma;\gamma,\delta)$
is differentiable at
![]() $\sigma=\alpha'$
with
$\sigma=\alpha'$
with
 \begin{align*}\phi_f'(\alpha';\gamma,\delta) &=\frac{\mathrm{d}}{\mathrm{d}\sigma}\left[\frac{1}{\delta-\gamma}\int_{\gamma}^{\delta}\log|f(\alpha'+it)|\mathrm{d}t\right]_{\sigma=\alpha'}\\&=\frac{1}{\delta-\gamma}\int_{\gamma}^{\delta}\left.\frac{\partial\log|f(\sigma+it)|}{\partial\sigma}\right|_{\sigma=\alpha'}\mathrm{d}t=\frac{1}{\delta-\gamma}\int_{\gamma}^{\delta}\mathrm{Re}\frac{f'(\alpha'+it)}{f(\alpha'+it)}\mathrm{d}t.\end{align*}
\begin{align*}\phi_f'(\alpha';\gamma,\delta) &=\frac{\mathrm{d}}{\mathrm{d}\sigma}\left[\frac{1}{\delta-\gamma}\int_{\gamma}^{\delta}\log|f(\alpha'+it)|\mathrm{d}t\right]_{\sigma=\alpha'}\\&=\frac{1}{\delta-\gamma}\int_{\gamma}^{\delta}\left.\frac{\partial\log|f(\sigma+it)|}{\partial\sigma}\right|_{\sigma=\alpha'}\mathrm{d}t=\frac{1}{\delta-\gamma}\int_{\gamma}^{\delta}\mathrm{Re}\frac{f'(\alpha'+it)}{f(\alpha'+it)}\mathrm{d}t.\end{align*}
Next we assume that f(s) has only one zero in the vertical segment
![]() $[\alpha'+i\gamma,\alpha'+i\delta]$
of order m,
$[\alpha'+i\gamma,\alpha'+i\delta]$
of order m,
![]() $\alpha'+it_0$
say. Then there is some
$\alpha'+it_0$
say. Then there is some
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
where g(s) is analytic and zero-free in the disk
![]() $|s-\alpha'-it_0|<2\varepsilon$
. Therefore,
$|s-\alpha'-it_0|<2\varepsilon$
. Therefore,
 \begin{align*}\frac{\mathrm{d}}{\mathrm{d}\sigma}&\left[\int_{t_0-\varepsilon}^{t_0+\varepsilon}\log|f(\sigma+it)|\mathrm{d}t\right]_{\sigma=\alpha'\pm0}\\&=\frac{\mathrm{d}}{\mathrm{d}\sigma}\left[\int_{t_0-\varepsilon}^{t_0+\varepsilon}m\log|\sigma-\alpha'+i(t-t_0)|+\log|g(\sigma+it)|\mathrm{d}t\right]_{\sigma=\alpha'\pm0}\\&=\lim_{\sigma\to\alpha'^\pm}\int_{t_0-\varepsilon}^{t_0+\varepsilon}\frac{m(\sigma-\alpha')\mathrm{d}t}{(\sigma-\alpha')^2+(t-t_0)^2}+\int_{t_0-\varepsilon}^{t_0+\varepsilon}\mathrm{Re}\frac{g'(\alpha'+it)}{g(\alpha'+it)}\mathrm{d}t\\&=\pm m\pi+\int_{t_0-\varepsilon}^{t_0+\varepsilon}\mathrm{Re}\frac{f'(\alpha'+it)}{f(\alpha'+it)}\mathrm{d}t.\end{align*}
\begin{align*}\frac{\mathrm{d}}{\mathrm{d}\sigma}&\left[\int_{t_0-\varepsilon}^{t_0+\varepsilon}\log|f(\sigma+it)|\mathrm{d}t\right]_{\sigma=\alpha'\pm0}\\&=\frac{\mathrm{d}}{\mathrm{d}\sigma}\left[\int_{t_0-\varepsilon}^{t_0+\varepsilon}m\log|\sigma-\alpha'+i(t-t_0)|+\log|g(\sigma+it)|\mathrm{d}t\right]_{\sigma=\alpha'\pm0}\\&=\lim_{\sigma\to\alpha'^\pm}\int_{t_0-\varepsilon}^{t_0+\varepsilon}\frac{m(\sigma-\alpha')\mathrm{d}t}{(\sigma-\alpha')^2+(t-t_0)^2}+\int_{t_0-\varepsilon}^{t_0+\varepsilon}\mathrm{Re}\frac{g'(\alpha'+it)}{g(\alpha'+it)}\mathrm{d}t\\&=\pm m\pi+\int_{t_0-\varepsilon}^{t_0+\varepsilon}\mathrm{Re}\frac{f'(\alpha'+it)}{f(\alpha'+it)}\mathrm{d}t.\end{align*}
It thus follows that
If f had more than one different zeros in
![]() $[\alpha'+i\gamma,\alpha'+i\delta]$
, then m would represent the sum of all such zeros counted with multiplicity. In view of (14) we deduce first that
$[\alpha'+i\gamma,\alpha'+i\delta]$
, then m would represent the sum of all such zeros counted with multiplicity. In view of (14) we deduce first that
![]() $m\pi=o(\delta-\gamma)$
,
$m\pi=o(\delta-\gamma)$
,
![]() $\delta-\gamma\to\infty$
, and then we obtain the desired relation (9).
$\delta-\gamma\to\infty$
, and then we obtain the desired relation (9).
The same reasoning applies in the strip of analytic continuation, where relation (13) still holds assuming the conditions of Theorem (B) (see Borchsenius and Jessen [Reference Borchsenius and Jessen4, page 122]).
Acknowledgments
We would like to thank the referee for carefully reading our work and pointing out some inaccuracies.