1 Introduction
In [Reference Sullivan35], Sullivan stated his structural stability theorem for group actions satisfying certain expansion-hyperbolicity axioms in the
![]() $C^1$
-setting. Its main application was to the stability for convex-cocompact Kleinian groups, but this particular result of Sullivan appears to have been relatively unknown (see Remark 4.7) presumably due to the lack of a detailed proof.
$C^1$
-setting. Its main application was to the stability for convex-cocompact Kleinian groups, but this particular result of Sullivan appears to have been relatively unknown (see Remark 4.7) presumably due to the lack of a detailed proof.
The goal of this paper is twofold. First, we generalize Sullivan’s result in two directions and provide a detailed proof along the way. We work with locally bi-Lipschitz group actions on geodesic metric spaces. We then weaken Sullivan’s axioms to what we call meandering hyperbolicity. This condition still implies the structural stability in the sense of Sullivan even though the groups need not be word-hyperbolic. Second, we establish some basic properties of meandering-hyperbolic actions and explore various examples of such actions, most unexpected among which are actions of uniform lattices in semisimple Lie groups on flag manifolds. As for word-hyperbolic groups, other interesting examples include Anosov actions on flag manifolds as well as actions with invariant subsets nonhomeomorphic to Gromov boundaries.
We now explain Sullivan’s structural stability theorem in more detail and exhibit the key idea of our generalization.
Theorem [Reference Sullivan35, §9. Theorem II]
Consider a group action
![]() $\Gamma \to \mathrm {Diff}^1(M)$
on a Riemannian manifold M with a compact invariant subset
$\Gamma \to \mathrm {Diff}^1(M)$
on a Riemannian manifold M with a compact invariant subset
![]() $\Lambda \subset M$
. If the action satisfies the expansion-hyperbolicity axioms, then it is structurally stable in the sense of
$\Lambda \subset M$
. If the action satisfies the expansion-hyperbolicity axioms, then it is structurally stable in the sense of
![]() $C^1$
-dynamics.
$C^1$
-dynamics.
Here, the expansion axiom means that for all
![]() $x\in \Lambda $
there exists
$x\in \Lambda $
there exists
![]() $g\in \Gamma $
such that
$g\in \Gamma $
such that
![]() $\|g'(x)\|>1$
with respect to the Riemannian metric. We generalize this condition accordingly for locally bi-Lipschitz actions on geodesic metric spaces (Definition 3.4). For each point
$\|g'(x)\|>1$
with respect to the Riemannian metric. We generalize this condition accordingly for locally bi-Lipschitz actions on geodesic metric spaces (Definition 3.4). For each point
![]() $x\in \Lambda $
, the expansion condition enables us to choose a sequence (called a code)
$x\in \Lambda $
, the expansion condition enables us to choose a sequence (called a code)
![]() $\alpha $
in a finite generating set of
$\alpha $
in a finite generating set of
![]() $\Gamma $
, along with the corresponding ray
$\Gamma $
, along with the corresponding ray
![]() $c^{\alpha }:\mathbb {N}_0\to \Gamma $
in (the Cayley graph of) the group
$c^{\alpha }:\mathbb {N}_0\to \Gamma $
in (the Cayley graph of) the group
![]() $\Gamma $
(Definitions 3.10 and 3.12).
$\Gamma $
(Definitions 3.10 and 3.12).
Sullivan’s hyperbolicity axiom, which we refer to as S-hyperbolicity (with the letter S standing for Sullivan), is an additional requirement to the expansion axiom, stating that any two rays associated to a point
![]() $x\in \Lambda $
are within Hausdorff distance N from each other for some uniform constant
$x\in \Lambda $
are within Hausdorff distance N from each other for some uniform constant
![]() $N>0$
(Definition 3.25), which is a form of the fellow-traveling condition. Under this condition, Sullivan’s theorem asserts that the action
$N>0$
(Definition 3.25), which is a form of the fellow-traveling condition. Under this condition, Sullivan’s theorem asserts that the action
![]() $\rho :\Gamma \to \mathrm {Diff}^1(M)$
is structurally stable in the sense of
$\rho :\Gamma \to \mathrm {Diff}^1(M)$
is structurally stable in the sense of
![]() $C^1$
-dynamics, that is, for every action
$C^1$
-dynamics, that is, for every action
![]() $\rho '$
sufficiently
$\rho '$
sufficiently
![]() $C^1$
-close to
$C^1$
-close to
![]() $\rho $
, there exists a
$\rho $
, there exists a
![]() $\rho '$
-invariant compact subset
$\rho '$
-invariant compact subset
![]() $\Lambda '\subset M$
and an equivariant homeomorphism
$\Lambda '\subset M$
and an equivariant homeomorphism
![]() $\phi :\Lambda \to \Lambda '$
. The S-hyperbolicity condition plays a critical role in defining the image
$\phi :\Lambda \to \Lambda '$
. The S-hyperbolicity condition plays a critical role in defining the image
![]() $\phi (x)$
unambiguously, regardless of the choice made for codes
$\phi (x)$
unambiguously, regardless of the choice made for codes
![]() $\alpha $
.
$\alpha $
.
The key point in our generalization is the simple observation that such a fellow-traveling property of rays in the S-hyperbolicity condition is too strong a requirement and that a much more relaxed equivalence relation between rays would still suffice for the existence of the map
![]() $\phi $
(Section 4.4). Namely, given two rays for a point in
$\phi $
(Section 4.4). Namely, given two rays for a point in
![]() $\Lambda $
, we require that they are Hausdorff-close only on infinite subsets of each. Furthermore, we allow interpolation of such a relation by other rays. The equivalence relation generated in this way is the main feature of our generalization of S-hyperbolicity, which we call the meandering hyperbolicity condition (Definition 3.26). See Remark 3.24(b) for our reasoning behind the nomenclature.
$\Lambda $
, we require that they are Hausdorff-close only on infinite subsets of each. Furthermore, we allow interpolation of such a relation by other rays. The equivalence relation generated in this way is the main feature of our generalization of S-hyperbolicity, which we call the meandering hyperbolicity condition (Definition 3.26). See Remark 3.24(b) for our reasoning behind the nomenclature.
With this relaxed definition, we generalize Sullivan’s structural stability theorem as follows. Let
![]() $\mathrm {LHomeo}(M)$
denote the group of locally bi-Lipschitz homeomorphisms of M.
$\mathrm {LHomeo}(M)$
denote the group of locally bi-Lipschitz homeomorphisms of M.
Theorem 1.1 (Theorem 4.4(1))
Consider an action
![]() $\Gamma \to \mathrm {LHomeo}(M)$
of a finitely generated group
$\Gamma \to \mathrm {LHomeo}(M)$
of a finitely generated group
![]() $\Gamma $
on a proper geodesic metric space M with a compact invariant subset
$\Gamma $
on a proper geodesic metric space M with a compact invariant subset
![]() $\Lambda \subset M$
, no point of which is isolated in M. If the action is meandering-hyperbolic, then it is structurally stable in the sense of Lipschitz dynamics.
$\Lambda \subset M$
, no point of which is isolated in M. If the action is meandering-hyperbolic, then it is structurally stable in the sense of Lipschitz dynamics.
See Theorem 4.4 for the full statement. We say that an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is structurally stable in the sense of Lipschitz dynamics if, for every action
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is structurally stable in the sense of Lipschitz dynamics if, for every action
![]() $\rho ':\Gamma \to \mathrm {LHomeo}(M)$
sufficiently close to
$\rho ':\Gamma \to \mathrm {LHomeo}(M)$
sufficiently close to
![]() $\rho $
with respect to the compact-open Lipschitz topology (see Section 4.1), there exists a
$\rho $
with respect to the compact-open Lipschitz topology (see Section 4.1), there exists a
![]() $\rho '$
-invariant subset
$\rho '$
-invariant subset
![]() $\Lambda '\subset M$
along with a topological conjugacy
$\Lambda '\subset M$
along with a topological conjugacy
![]() $\phi :\Lambda \to \Lambda '$
.
$\phi :\Lambda \to \Lambda '$
.
This generalization of Sullivan’s theorem is general enough to encompass actions of certain nonhyperbolic groups as we exhibit below. Its proof will take the entire Section 4. We mostly follow Sullivan’s idea of proof, filling in the details he sometimes left out, except in Section 4.4, where the meandering hyperbolicity condition comes in and plays a crucial role, and in Sections 4.9 and 4.10, which are not covered in his paper.
We investigate various examples of expanding and meandering-hyperbolic actions. Most significantly, in Section 5, we establish the following result regarding uniform lattices of semisimple Lie groups:
Theorem 1.2 (Theorem 5.1 and Corollary 5.2)
Suppose that G is a semisimple Lie group,
![]() $P< G$
is a parabolic subgroup and
$P< G$
is a parabolic subgroup and
![]() $\Gamma < G$
is a uniform lattice. Then
$\Gamma < G$
is a uniform lattice. Then
-
(1) the
 $\Gamma $
-action on the flag manifold
$\Gamma $
-action on the flag manifold
 $G/P$
is (uniformly) meandering-hyperbolic;
$G/P$
is (uniformly) meandering-hyperbolic; -
(2) consequently, the action is structurally stable in the sense of Lipschitz dynamics.
While stability of the action is consistent with various other rigidity properties of uniform lattices, the hyperbolic nature of the actions of higher rank uniform lattices on flag manifolds is a new phenomenon: Higher rank uniform lattices are traditionally regarded as having no hyperbolic features. The main tools in proving Theorem 1.2(1) are Morse quasi-geodesics in higher rank symmetric spaces and asymptotic properties of regular sequences in G, established in earlier papers by Kapovich, Leeb and Porti [Reference Kapovich and Leeb23, Reference Kapovich, Leeb and Porti26, Reference Kapovich, Leeb and Porti27].
We hope that other interesting nonhyperbolic group actions satisfy meandering hyperbolicity as well. For example:
Conjecture 1.3. Let
![]() $\Gamma $
be a group of automorphisms of a
$\Gamma $
be a group of automorphisms of a
![]() $\mathrm {CAT}(0)$
cube complex X, acting on X properly discontinuously and cocompactly. Then the action of
$\mathrm {CAT}(0)$
cube complex X, acting on X properly discontinuously and cocompactly. Then the action of
![]() $\Gamma $
on the Roller boundary
$\Gamma $
on the Roller boundary
![]() $\partial _R X$
of X is meandering-hyperbolic for a suitable metric on
$\partial _R X$
of X is meandering-hyperbolic for a suitable metric on
![]() $\partial _R X$
.
$\partial _R X$
.
Even for word-hyperbolic groups
![]() $\Gamma $
, meandering-hyperbolic actions
$\Gamma $
, meandering-hyperbolic actions
![]() $\Gamma \to \mathrm {LHomeo}(M)$
provide interesting results and examples. In this setting, we find a relation between the
$\Gamma \to \mathrm {LHomeo}(M)$
provide interesting results and examples. In this setting, we find a relation between the
![]() $\Gamma $
-invariant set
$\Gamma $
-invariant set
![]() $\Lambda $
and the Gromov boundary
$\Lambda $
and the Gromov boundary
![]() $\partial _{\infty }\Gamma $
of
$\partial _{\infty }\Gamma $
of
![]() $\Gamma $
as follows.
$\Gamma $
as follows.
Theorem 1.4 (Definition 6.1 and Theorem 6.8)
Let
![]() $\Gamma $
be a nonelementary word-hyperbolic group. If
$\Gamma $
be a nonelementary word-hyperbolic group. If
![]() $\Gamma \to \mathrm {LHomeo}(M)$
is a meandering-hyperbolic action with a compact invariant subset
$\Gamma \to \mathrm {LHomeo}(M)$
is a meandering-hyperbolic action with a compact invariant subset
![]() $\Lambda $
, then there exists an equivariant continuous surjective postal map
$\Lambda $
, then there exists an equivariant continuous surjective postal map
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
to the Gromov boundary of
$\pi :\Lambda \to \partial _{\infty }\Gamma $
to the Gromov boundary of
![]() $\Gamma $
; the map
$\Gamma $
; the map
![]() $\pi $
restricts to a quasi-open map on each minimal nonempty closed
$\pi $
restricts to a quasi-open map on each minimal nonempty closed
![]() $\Gamma $
-invariant subset
$\Gamma $
-invariant subset
![]() $\Lambda _{\mu }\subset \Lambda $
.
$\Lambda _{\mu }\subset \Lambda $
.
Here, a map between topological spaces is said to be nowhere constant (resp. quasi-open) if the image of every nonempty open subset is not a singleton (resp. has nonempty interior).
We then explore examples of meandering-hyperbolic actions of word-hyperbolic groups where the postal maps
![]() $\pi $
above are increasingly more complicated. Simple examples are convex-cocompact Kleinian groups and, more generally, Anosov subgroups (see Section 2.4), for which the invariant subsets
$\pi $
above are increasingly more complicated. Simple examples are convex-cocompact Kleinian groups and, more generally, Anosov subgroups (see Section 2.4), for which the invariant subsets
![]() $\Lambda $
are equivariantly homeomorphic to the Gromov boundary
$\Lambda $
are equivariantly homeomorphic to the Gromov boundary
![]() $\partial _{\infty }\Gamma $
(via the postal map
$\partial _{\infty }\Gamma $
(via the postal map
![]() $\pi $
). In contrast, there are examples where the postal map
$\pi $
). In contrast, there are examples where the postal map
![]() $\pi $
can be a covering map (Examples 7.3 and 7.4), can be open but fail to be a local homeomorphism (Example 7.5) and can even fail to be an open map (Example 7.6).
$\pi $
can be a covering map (Examples 7.3 and 7.4), can be open but fail to be a local homeomorphism (Example 7.5) and can even fail to be an open map (Example 7.6).
Conversely to Theorem 1.4, we also prove:
Theorem 1.5 (Theorem 6.2)
Let
![]() $\Gamma $
be a nonelementary word-hyperbolic group. Suppose that
$\Gamma $
be a nonelementary word-hyperbolic group. Suppose that
![]() $\Gamma \to \mathrm {LHomeo}(M)$
is an action expanding at
$\Gamma \to \mathrm {LHomeo}(M)$
is an action expanding at
![]() $\Lambda $
, for which there exists an equivariant continuous nowhere constant map
$\Lambda $
, for which there exists an equivariant continuous nowhere constant map
![]() $f:\Lambda \to \partial _{\infty }\Gamma $
. Then the
$f:\Lambda \to \partial _{\infty }\Gamma $
. Then the
![]() $\Gamma $
-action is S-hyperbolic (and thus, meandering-hyperbolic) at
$\Gamma $
-action is S-hyperbolic (and thus, meandering-hyperbolic) at
![]() $\Lambda $
and the map f equals the postal map
$\Lambda $
and the map f equals the postal map
![]() $\pi $
(of the previous theorem).
$\pi $
(of the previous theorem).
We note that in the case of real-analytic expanding
![]() $\Gamma $
-actions on the circle, a sharper result is proven by Deroin in [Reference Deroin14]. Without assuming hyperbolicity of
$\Gamma $
-actions on the circle, a sharper result is proven by Deroin in [Reference Deroin14]. Without assuming hyperbolicity of
![]() $\Gamma $
(he only assumes finite generation and local discreteness of the action), Deroin proves that the action comes from a lift of a Fuchsian group action under a finite covering map
$\Gamma $
(he only assumes finite generation and local discreteness of the action), Deroin proves that the action comes from a lift of a Fuchsian group action under a finite covering map
![]() $S^1\to S^1$
. Compare Example 7.3.
$S^1\to S^1$
. Compare Example 7.3.
Building upon the work in [Reference Kapovich, Leeb and Porti26] and Theorem 1.5, we give a (yet another) new characterization of Anosov subgroups in terms of expanding actions. See Theorem 6.12. This characterization shows, among other things, that the action of any Anosov group on its flag-limit set in the partial flag manifold is S-hyperbolic. Thus, thanks to Theorem 1.1, we obtain the stability of Anosov groups in a broader context than those in [Reference Guichard and Wienhard19, Theorem 5.13] and [Reference Kapovich, Leeb and Porti24, Theorems 1.11 and 7.36]. Based on this, we also obtain an alternative proof for the openness of the Anosov property in the representation variety (Corollary 6.14).
We remark that Bochi, Potrie and Sambarino [Reference Bochi, Potrie and Sambarino3] gave a purely dynamical proof of the structural stability of Anosov representations, which shares many similarities with the concepts in the present paper. For example, one may compare the expansion subsets with the notion of multicones in [Reference Bochi, Potrie and Sambarino3, Section 5]. The existence of codings appears in [Reference Bochi, Potrie and Sambarino3, Lemma 3.20] and the expansion property in [Reference Bochi, Potrie and Sambarino3, Lemma 3.21]. (We thank the referee for pointing out these similarities to us.) On the other hand, in the setting of S-hyperbolic actions, such as Anosov actions, all the ideas in the proof of Theorem 1.1 go back to Sullivan’s original paper [Reference Sullivan35].
After the initial version of this paper was completed, Mann and Manning posted an interesting preprint [Reference Mann and Manning29] related to the main theme of our paper: They prove topological stability of word-hyperbolic group actions on their boundaries under the assumption that the latter are topological spheres. Unlike our work, they only assume
![]() $C^0$
rather than Lipschitz perturbation.
$C^0$
rather than Lipschitz perturbation.
2 Notation and preliminaries
The identity element of an abstract group will be denoted by e. We will use the following notation for the sets of nonnegative integers and natural numbers:
We will follow the Bourbaki convention that neighborhoods of a point a (resp. a subset A) in a topological space X need not be open but are only required to contain an open subset which, in turn, contains a (resp. A). In particular, a topological space X is locally compact if and only if every point in X admits a neighborhood basis consisting of compact subsets of X.
A topological space is called perfect if it has no isolated points and has cardinality
![]() $\ge 2$
.
$\ge 2$
.
A map between topological spaces is nowhere constant if the image of every open subset is not a singleton. A map is said to be open if it sends open sets to open sets. A map
![]() $f:X\to Y$
is open at a point
$f:X\to Y$
is open at a point
![]() $x\in X$
if it sends every neighborhood of x to a neighborhood of
$x\in X$
if it sends every neighborhood of x to a neighborhood of
![]() $f(x)$
. We let
$f(x)$
. We let
![]() $O_f$
denote the subset of X consisting of points where f is open. Thus, a map f is open if and only if
$O_f$
denote the subset of X consisting of points where f is open. Thus, a map f is open if and only if
![]() $O_f= X$
.
$O_f= X$
.
A map
![]() $f: X\to Y$
is said to be quasi-open (or quasi-interior) if, for every subset
$f: X\to Y$
is said to be quasi-open (or quasi-interior) if, for every subset
![]() $A\subset X$
with nonempty interior, the image
$A\subset X$
with nonempty interior, the image
![]() $f(A)$
has nonempty interior in Y. If
$f(A)$
has nonempty interior in Y. If
![]() $f:X\to Y$
is a continuous map between locally compact metrizable spaces then it is quasi-open if and only if the subset
$f:X\to Y$
is a continuous map between locally compact metrizable spaces then it is quasi-open if and only if the subset
![]() $O_f\subset X$
is comeagre (that is, its complement is a countable union of nowhere dense subsets). For instance, the map
$O_f\subset X$
is comeagre (that is, its complement is a countable union of nowhere dense subsets). For instance, the map
![]() $\mathbb {R}\to \mathbb {R}, x\mapsto x^2$
, is quasi-open but not open. A more interesting example of a (nonopen) quasi-open map is a Cantor function
$\mathbb {R}\to \mathbb {R}, x\mapsto x^2$
, is quasi-open but not open. A more interesting example of a (nonopen) quasi-open map is a Cantor function
![]() $f:C\to [0,1]$
, which is a continuous surjective monotonic function from a Cantor set
$f:C\to [0,1]$
, which is a continuous surjective monotonic function from a Cantor set
![]() $C\subset \mathbb {R}$
. It has the property that
$C\subset \mathbb {R}$
. It has the property that
![]() $x_1<x_2$
implies
$x_1<x_2$
implies
![]() $f(x_1)< f(x_2)$
unless
$f(x_1)< f(x_2)$
unless
![]() $x_1, x_2$
are boundary points of a component of
$x_1, x_2$
are boundary points of a component of
![]() $\mathbb {R}-C$
. Thus,
$\mathbb {R}-C$
. Thus,
![]() $C-O_f$
is the countable subset consisting of boundary points of components of
$C-O_f$
is the countable subset consisting of boundary points of components of
![]() $\mathbb {R}-C$
.
$\mathbb {R}-C$
.
Let
![]() $(X,d)$
be a metric space. Given
$(X,d)$
be a metric space. Given
![]() $x\in X$
and
$x\in X$
and
![]() $r>0$
, the open (resp. closed) r-ball centered at x is denoted by
$r>0$
, the open (resp. closed) r-ball centered at x is denoted by
![]() $B_r(x)$
(resp.
$B_r(x)$
(resp.
![]() $\overline {B}_r(x)$
). Given a subset
$\overline {B}_r(x)$
). Given a subset
![]() $\Lambda \subset X$
, its open (resp. closed) r-neighborhood is denoted by
$\Lambda \subset X$
, its open (resp. closed) r-neighborhood is denoted by
![]() $N_r(\Lambda )$
(resp.
$N_r(\Lambda )$
(resp.
![]() $\overline {N}_r(\Lambda )$
). A Lebesgue number of an open cover
$\overline {N}_r(\Lambda )$
). A Lebesgue number of an open cover
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\Lambda $
is defined to be a number
$\Lambda $
is defined to be a number
![]() $\delta>0$
such that, for every
$\delta>0$
such that, for every
![]() $x\in \Lambda $
, the
$x\in \Lambda $
, the
![]() $\delta $
-ball
$\delta $
-ball
![]() $B_{\delta }(x)$
is contained in some member of
$B_{\delta }(x)$
is contained in some member of
![]() $\mathcal {U}$
; we denote
$\mathcal {U}$
; we denote
For a subset
![]() $U\subset X$
and
$U\subset X$
and
![]() $r>0$
, we define
$r>0$
, we define
A sequence of subsets
![]() $W_k\subset X$
is said to be exponentially shrinking if the diameters of these subsets converge to zero exponentially fast, that is, there exist constants
$W_k\subset X$
is said to be exponentially shrinking if the diameters of these subsets converge to zero exponentially fast, that is, there exist constants
![]() $A,C>0$
such that
$A,C>0$
such that
for all k.
If X is a Riemannian manifold and
![]() $\Phi $
is a diffeomorphism of X, the expansion factor of
$\Phi $
is a diffeomorphism of X, the expansion factor of
![]() $\Phi $
at
$\Phi $
at
![]() $x\in X$
is defined as
$x\in X$
is defined as
 $$ \begin{align} \mathcal E(\Phi,x)=\inf_{0\neq v\in T_x X}\frac{\|D_x\Phi(v)\|}{\|v\|}. \end{align} $$
$$ \begin{align} \mathcal E(\Phi,x)=\inf_{0\neq v\in T_x X}\frac{\|D_x\Phi(v)\|}{\|v\|}. \end{align} $$
We now present some dynamical and geometric preliminaries to be used later. For more details, we refer the readers to [Reference Bridson and Haeiger7] and [Reference Druţu and Kapovich15].
2.1 Topological dynamics
A continuous action
![]() $\Gamma \times Z\to Z$
of a topological group on a topological space is minimal if Z contains no proper closed
$\Gamma \times Z\to Z$
of a topological group on a topological space is minimal if Z contains no proper closed
![]() $\Gamma $
-invariant subsets or, equivalently, if every
$\Gamma $
-invariant subsets or, equivalently, if every
![]() $\Gamma $
-orbit is dense in Z. A point
$\Gamma $
-orbit is dense in Z. A point
![]() $z\in Z$
is a wandering point for an action
$z\in Z$
is a wandering point for an action
![]() $\Gamma \times Z\to Z$
if there exists a neighborhood U of z such that
$\Gamma \times Z\to Z$
if there exists a neighborhood U of z such that
![]() $g U\cap U=\emptyset $
for all but finitely many
$g U\cap U=\emptyset $
for all but finitely many
![]() $g\in \Gamma $
. If the space Z is metrizable, then a point
$g\in \Gamma $
. If the space Z is metrizable, then a point
![]() $z\in Z$
is not a wandering point if and only if there exist a sequence
$z\in Z$
is not a wandering point if and only if there exist a sequence
![]() $(g_k)$
of distinct elements in
$(g_k)$
of distinct elements in
![]() $\Gamma $
and a sequence
$\Gamma $
and a sequence
![]() $(z_k)$
in Z converging to z such that
$(z_k)$
in Z converging to z such that
![]() $g_kz_k\to z$
. For further discussion of dynamical relations between points under group actions, see [Reference Kapovich and Leeb22, §4.3].
$g_kz_k\to z$
. For further discussion of dynamical relations between points under group actions, see [Reference Kapovich and Leeb22, §4.3].
A continuous action
![]() $\Gamma \times Z\to Z$
of a discrete group
$\Gamma \times Z\to Z$
of a discrete group
![]() $\Gamma $
on a compact metrizable topological space Z is a convergence action if the product action of
$\Gamma $
on a compact metrizable topological space Z is a convergence action if the product action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $Z^3$
restricts to a properly discontinuous action on
$Z^3$
restricts to a properly discontinuous action on
Equivalently, a continuous action of a discrete group is a convergence action if every sequence
![]() $(g_k)$
contains a subsequence
$(g_k)$
contains a subsequence
![]() $(g_{k_j})$
which is constant or converges to a point
$(g_{k_j})$
which is constant or converges to a point
![]() $z_+\in Z$
uniformly on compacts in
$z_+\in Z$
uniformly on compacts in
![]() $Z-\{z_-\}$
for some
$Z-\{z_-\}$
for some
![]() $z_-\in Z$
; see [Reference Bowditch6, Proposition 7.1]. In this situation, the inverse sequence
$z_-\in Z$
; see [Reference Bowditch6, Proposition 7.1]. In this situation, the inverse sequence
![]() $(g_{k_j}^{-1})$
converges to
$(g_{k_j}^{-1})$
converges to
![]() $z_-$
uniformly on compacts in
$z_-$
uniformly on compacts in
![]() $Z-\{z_+\}$
. The set of such limit points
$Z-\{z_+\}$
. The set of such limit points
![]() $z_+$
is the limit set
$z_+$
is the limit set
![]() $\Lambda $
of the action of
$\Lambda $
of the action of
![]() $\Gamma $
; this is a closed
$\Gamma $
; this is a closed
![]() $\Gamma $
-invariant subset of Z. Observe that a convergence action need not be faithful but it necessarily has finite kernel, provided that
$\Gamma $
-invariant subset of Z. Observe that a convergence action need not be faithful but it necessarily has finite kernel, provided that
![]() $T(Z)\ne \emptyset $
. A convergence action on Z is called uniform if it is cocompact on
$T(Z)\ne \emptyset $
. A convergence action on Z is called uniform if it is cocompact on
![]() $T(Z)$
.
$T(Z)$
.
Remark 2.3. Since proper discontinuity of an action is preserved under taking subgroups, if the action of
![]() $\Gamma $
on Z is a convergence action, then its restriction to any subgroup
$\Gamma $
on Z is a convergence action, then its restriction to any subgroup
![]() $\Gamma _0<\Gamma $
is still a convergence action.
$\Gamma _0<\Gamma $
is still a convergence action.
Item (1) of the following theorem can be found in [Reference Tukia36, Theorem 2S]; for item (2) see [Reference Tukia37, Theorem 1A] for instance.
Theorem 2.4. Suppose
![]() $\Gamma \times Z\to Z$
is a convergence action with limit set
$\Gamma \times Z\to Z$
is a convergence action with limit set
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\mathrm {card}(\Lambda )\ge 3$
. Then
$\mathrm {card}(\Lambda )\ge 3$
. Then
-
(1)
 $\Lambda $
is perfect and the action is minimal on
$\Lambda $
is perfect and the action is minimal on
 $\Lambda $
.
$\Lambda $
. -
(2) If the action is uniform and Z is perfect, then
 $Z=\Lambda $
.
$Z=\Lambda $
.
2.2 Coarse geometry
A metric space
![]() $(X,d)$
is proper if the closed ball
$(X,d)$
is proper if the closed ball
![]() $\overline {B}_r(x)$
is compact for every
$\overline {B}_r(x)$
is compact for every
![]() $x\in X$
and every
$x\in X$
and every
![]() $r>0$
. Note that proper metric spaces are complete. A metric space
$r>0$
. Note that proper metric spaces are complete. A metric space
![]() $(X,d)$
is called a geodesic space if every pair of points
$(X,d)$
is called a geodesic space if every pair of points
![]() $x,y \in X$
can be joined by a geodesic segment
$x,y \in X$
can be joined by a geodesic segment
![]() $xy$
, that is, an isometric embedding of an interval into X joining x to y.
$xy$
, that is, an isometric embedding of an interval into X joining x to y.
Definition 2.5 (Quasi-geodesic)
Let I be an interval of
![]() $\mathbb {R}$
(or its intersection with
$\mathbb {R}$
(or its intersection with
![]() $\mathbb {Z}$
) and
$\mathbb {Z}$
) and
![]() $(X,d)$
a metric space. A map
$(X,d)$
a metric space. A map
![]() $c:I\to X$
is called an
$c:I\to X$
is called an
![]() $(A,C)$
-quasi-geodesic with constants
$(A,C)$
-quasi-geodesic with constants
![]() $A\geq 1$
and
$A\geq 1$
and
![]() $C\geq 0$
if for all
$C\geq 0$
if for all
![]() $t,t'\in I$
,
$t,t'\in I$
,
Definition 2.6 (Hyperbolic space)
Let
![]() $\delta \ge 0$
. A geodesic space X is said to be
$\delta \ge 0$
. A geodesic space X is said to be
![]() $\delta $
-hyperbolic if, for any geodesic triangle in X, each side of the triangle is contained in the closed
$\delta $
-hyperbolic if, for any geodesic triangle in X, each side of the triangle is contained in the closed
![]() $\delta $
-neighborhood of the union of the other two sides. A geodesic space is said to be hyperbolic if it is
$\delta $
-neighborhood of the union of the other two sides. A geodesic space is said to be hyperbolic if it is
![]() $\delta $
-hyperbolic for some
$\delta $
-hyperbolic for some
![]() $\delta \ge 0$
.
$\delta \ge 0$
.
Let X be a proper
![]() $\delta $
-hyperbolic space. Two geodesic rays
$\delta $
-hyperbolic space. Two geodesic rays
![]() $\mathbb {R}_{\ge 0}\to X$
are said to be asymptotic if the Hausdorff distance between their images is finite. Being asymptotic is an equivalence relation on the set of geodesic rays. The set of equivalence classes of geodesic rays in X is called the visual boundary of X and denoted by
$\mathbb {R}_{\ge 0}\to X$
are said to be asymptotic if the Hausdorff distance between their images is finite. Being asymptotic is an equivalence relation on the set of geodesic rays. The set of equivalence classes of geodesic rays in X is called the visual boundary of X and denoted by
![]() $\partial _{\infty } X$
. In view of the Morse lemma for hyperbolic spaces (see [Reference Bridson and Haeiger7, Theorem III.H.1.7] or [Reference Druţu and Kapovich15, Lemma 11.105] for example), one can also define
$\partial _{\infty } X$
. In view of the Morse lemma for hyperbolic spaces (see [Reference Bridson and Haeiger7, Theorem III.H.1.7] or [Reference Druţu and Kapovich15, Lemma 11.105] for example), one can also define
![]() $\partial _{\infty } X$
as the set of equivalence classes of quasi-geodesic rays
$\partial _{\infty } X$
as the set of equivalence classes of quasi-geodesic rays
![]() $\mathbb {R}_{\ge 0}\to X$
. We will use the notation
$\mathbb {R}_{\ge 0}\to X$
. We will use the notation
![]() $x\xi $
for a geodesic ray in X emanating from x and representing the point
$x\xi $
for a geodesic ray in X emanating from x and representing the point
![]() $\xi \in \partial _{\infty } X$
.
$\xi \in \partial _{\infty } X$
.
Fix
![]() $r>2\delta $
and let
$r>2\delta $
and let
![]() $c_0:\mathbb {R}_{\ge 0}\to X$
be a geodesic ray representing
$c_0:\mathbb {R}_{\ge 0}\to X$
be a geodesic ray representing
![]() $\xi \in \partial _{\infty } X$
with
$\xi \in \partial _{\infty } X$
with
![]() $c_0(0)=x$
. A topology on
$c_0(0)=x$
. A topology on
![]() $\partial _{\infty } X$
is given by setting the basis of neighborhoods of
$\partial _{\infty } X$
is given by setting the basis of neighborhoods of
![]() $\xi $
to be the collection
$\xi $
to be the collection
![]() $\{V_k(\xi )\}_{k\in \mathbb {N}}$
, where
$\{V_k(\xi )\}_{k\in \mathbb {N}}$
, where
![]() $V_k(\xi )$
is the set of equivalence classes of geodesic rays c such that
$V_k(\xi )$
is the set of equivalence classes of geodesic rays c such that
![]() $c(0)=x$
and
$c(0)=x$
and
![]() $d(c(k),c_0(k))<r$
. This topology extends to the visual compactification of X
$d(c(k),c_0(k))<r$
. This topology extends to the visual compactification of X
which is a compact metrizable space. We refer to [Reference Bridson and Haeiger7, III.H.3.6] for details.
Let
![]() $x,y,z \in X$
. The Gromov product of y and z with respect to x is defined by
$x,y,z \in X$
. The Gromov product of y and z with respect to x is defined by
The Gromov product is extended to
![]() $X\cup \partial _{\infty } X$
by
$X\cup \partial _{\infty } X$
by
where the supremum is taken over all sequences
![]() $(y_k)$
and
$(y_k)$
and
![]() $(z_j)$
in X such that
$(z_j)$
in X such that
![]() $\lim y_k=y$
and
$\lim y_k=y$
and
![]() $\lim z_j=z$
.
$\lim z_j=z$
.
Definition 2.7 (Visual metric)
Let X be a hyperbolic space with base point
![]() $x\in X$
. A metric
$x\in X$
. A metric
![]() $d_a$
on
$d_a$
on
![]() $\partial _{\infty } X$
is called a visual metric with parameter
$\partial _{\infty } X$
is called a visual metric with parameter
![]() $a>1$
if there exist constants
$a>1$
if there exist constants
![]() $k_1, k_2>0$
such that
$k_1, k_2>0$
such that
for all
![]() $\xi ,\xi '\in \partial _{\infty } X$
.
$\xi ,\xi '\in \partial _{\infty } X$
.
For every
![]() $a>1$
sufficiently close to
$a>1$
sufficiently close to
![]() $1$
, a proper hyperbolic space admits a visual metric
$1$
, a proper hyperbolic space admits a visual metric
![]() $d_a$
which induces the same topology as the topology on
$d_a$
which induces the same topology as the topology on
![]() $\partial _{\infty } X$
described above. We refer to [Reference Bridson and Haeiger7, Chapter III.H.3] for more details on constructing visual metrics.
$\partial _{\infty } X$
described above. We refer to [Reference Bridson and Haeiger7, Chapter III.H.3] for more details on constructing visual metrics.
In the rest of the section, we discuss hyperbolic groups and their relation to convergence actions.
Definition 2.8 (Hyperbolic group)
A finitely generated group
![]() $\Gamma $
is word-hyperbolic (or simply hyperbolic) if its Cayley graph with respect to a finite generating set of
$\Gamma $
is word-hyperbolic (or simply hyperbolic) if its Cayley graph with respect to a finite generating set of
![]() $\Gamma $
is a hyperbolic metric space. A hyperbolic group is called elementary if it contains a cyclic subgroup of finite index and nonelementary otherwise.
$\Gamma $
is a hyperbolic metric space. A hyperbolic group is called elementary if it contains a cyclic subgroup of finite index and nonelementary otherwise.
The Gromov boundary
![]() $\partial _{\infty }\Gamma $
of a hyperbolic group
$\partial _{\infty }\Gamma $
of a hyperbolic group
![]() $\Gamma $
is defined as the visual boundary of a Cayley graph X of
$\Gamma $
is defined as the visual boundary of a Cayley graph X of
![]() $\Gamma $
. The closure of
$\Gamma $
. The closure of
![]() $\Gamma \subset X$
in the visual compactification
$\Gamma \subset X$
in the visual compactification
![]() $\overline {X}$
equals
$\overline {X}$
equals
![]() $\Gamma \cup \partial _{\infty } \Gamma $
and is denoted
$\Gamma \cup \partial _{\infty } \Gamma $
and is denoted
![]() $\overline \Gamma $
; it is the visual compactification of
$\overline \Gamma $
; it is the visual compactification of
![]() $\Gamma $
.
$\Gamma $
.
Every hyperbolic group
![]() $\Gamma $
acts on its visual compactification
$\Gamma $
acts on its visual compactification
![]() $\overline {\Gamma }$
by homeomorphisms. This action is a convergence action; see [Reference Tukia36, Theorem 3.A] and [Reference Freden17]. If a sequence
$\overline {\Gamma }$
by homeomorphisms. This action is a convergence action; see [Reference Tukia36, Theorem 3.A] and [Reference Freden17]. If a sequence
![]() $(c_k)$
in
$(c_k)$
in
![]() $\Gamma $
represents a quasi-geodesic ray within bounded distance from a geodesic ray
$\Gamma $
represents a quasi-geodesic ray within bounded distance from a geodesic ray
![]() $g\xi $
(
$g\xi $
(
![]() $g\in \Gamma $
,
$g\in \Gamma $
,
![]() $\xi \in \partial _{\infty }\Gamma $
), then this sequence, regarded as a sequence of maps
$\xi \in \partial _{\infty }\Gamma $
), then this sequence, regarded as a sequence of maps
![]() $\overline \Gamma \to \overline \Gamma $
, converges to
$\overline \Gamma \to \overline \Gamma $
, converges to
![]() $\xi $
uniformly on compacts in
$\xi $
uniformly on compacts in
![]() $\overline \Gamma -\{\xi '\}$
for some
$\overline \Gamma -\{\xi '\}$
for some
![]() $\xi '\in \partial _{\infty }\Gamma $
. We will use the following refinement of this property later in the proof of Theorem 6.2:
$\xi '\in \partial _{\infty }\Gamma $
. We will use the following refinement of this property later in the proof of Theorem 6.2:
Lemma 2.9. Let
![]() $\Gamma $
be a word-hyperbolic group. Suppose that
$\Gamma $
be a word-hyperbolic group. Suppose that
![]() $c:\mathbb {N}_0\to \Gamma $
,
$c:\mathbb {N}_0\to \Gamma $
,
![]() $k\mapsto c_k$
, is an
$k\mapsto c_k$
, is an
![]() $(A,C)$
-quasi-geodesic ray in
$(A,C)$
-quasi-geodesic ray in
![]() $\Gamma $
such that
$\Gamma $
such that
-
• the word length of
 $c_0$
is
$c_0$
is
 $\le 1$
, and
$\le 1$
, and -
• there exists a subsequence
 $(c_{k_j})$
converging to a point
$(c_{k_j})$
converging to a point
 $\xi \in \partial _{\infty }\Gamma $
pointwise on a subset
$\xi \in \partial _{\infty }\Gamma $
pointwise on a subset
 $S\subset \partial _{\infty }\Gamma $
with
$S\subset \partial _{\infty }\Gamma $
with
 $\mathrm {card}(S)\ge 2$
.
$\mathrm {card}(S)\ge 2$
.
Then the image
![]() $c(\mathbb {N}_0)$
is D-Hausdorff close to a geodesic
$c(\mathbb {N}_0)$
is D-Hausdorff close to a geodesic
![]() $e\xi $
in the Cayley graph X of
$e\xi $
in the Cayley graph X of
![]() $\Gamma $
, where D depends only on
$\Gamma $
, where D depends only on
![]() $(A,C)$
and the hyperbolicity constant of X.
$(A,C)$
and the hyperbolicity constant of X.
Proof. Since the word length of
![]() $c_0$
is
$c_0$
is
![]() $\le 1$
, the extended Morse lemma for hyperbolic groups in [Reference Druţu and Kapovich15, Lemma 11.105] states that there is a geodesic ray
$\le 1$
, the extended Morse lemma for hyperbolic groups in [Reference Druţu and Kapovich15, Lemma 11.105] states that there is a geodesic ray
![]() $e\mu $
(
$e\mu $
(
![]() $\mu \in \partial _{\infty }\Gamma $
) starting at the identity
$\mu \in \partial _{\infty }\Gamma $
) starting at the identity
![]() $e\in \Gamma $
such that the Hausdorff distance between the image
$e\in \Gamma $
such that the Hausdorff distance between the image
![]() $c(\mathbb {N}_0)$
and the ray
$c(\mathbb {N}_0)$
and the ray
![]() $e\mu $
in X is bounded above by a uniform constant
$e\mu $
in X is bounded above by a uniform constant
![]() $D>0$
depending only on
$D>0$
depending only on
![]() $(A,C)$
and X.
$(A,C)$
and X.
By the above property, the sequence
![]() $(c_k)$
converges to
$(c_k)$
converges to
![]() $\mu $
uniformly on compacts in
$\mu $
uniformly on compacts in
![]() $\overline \Gamma -\{\mu '\}$
for some
$\overline \Gamma -\{\mu '\}$
for some
![]() $\mu '\in \partial _{\infty }\Gamma $
. On the other hand, since
$\mu '\in \partial _{\infty }\Gamma $
. On the other hand, since
![]() $\mathrm {card}(S)\ge 2$
, there is a point
$\mathrm {card}(S)\ge 2$
, there is a point
![]() $\nu \in S$
distinct from
$\nu \in S$
distinct from
![]() $\mu '$
such that the subsequence
$\mu '$
such that the subsequence
![]() $(c_{k_j})$
converges to
$(c_{k_j})$
converges to
![]() $\xi $
on
$\xi $
on
![]() $\{\nu \}\subset \partial _{\infty }\Gamma $
. Therefore, we must have
$\{\nu \}\subset \partial _{\infty }\Gamma $
. Therefore, we must have
![]() $\mu =\xi $
and
$\mu =\xi $
and
![]() $e\mu =e\xi $
.
$e\mu =e\xi $
.
Furthermore, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\partial _{\infty }\Gamma $
is a uniform convergence action. In particular, if
$\partial _{\infty }\Gamma $
is a uniform convergence action. In particular, if
![]() $\Gamma $
is nonelementary, then this action has finite kernel (the unique maximal finite normal subgroup of
$\Gamma $
is nonelementary, then this action has finite kernel (the unique maximal finite normal subgroup of
![]() $\Gamma $
), is minimal and
$\Gamma $
), is minimal and
![]() $\partial _{\infty }\Gamma $
is a perfect topological space; compare Theorem 2.4. We refer to [Reference Druţu and Kapovich15, Lemma 11.130] for more details.
$\partial _{\infty }\Gamma $
is a perfect topological space; compare Theorem 2.4. We refer to [Reference Druţu and Kapovich15, Lemma 11.130] for more details.
Conversely, Bowditch [Reference Bowditch6] gave a topological characterization of hyperbolic groups and their Gromov boundaries as uniform convergence actions
![]() $\Gamma \times Z\to Z$
of discrete groups on perfect metrizable topological spaces:
$\Gamma \times Z\to Z$
of discrete groups on perfect metrizable topological spaces:
Theorem 2.10 (Bowditch)
Suppose that Z is a compact perfect metrizable space of cardinality
![]() $\ge 2$
and
$\ge 2$
and
![]() $\Gamma \times Z\to Z$
is a continuous action of a discrete group, which is a uniform convergence action. Then
$\Gamma \times Z\to Z$
is a continuous action of a discrete group, which is a uniform convergence action. Then
![]() $\Gamma $
is a nonelementary hyperbolic group and Z is equivariantly homeomorphic to the Gromov boundary
$\Gamma $
is a nonelementary hyperbolic group and Z is equivariantly homeomorphic to the Gromov boundary
![]() $\partial _{\infty }\Gamma $
.
$\partial _{\infty }\Gamma $
.
2.3 Symmetric spaces
We collect several definitions regarding the geometry of symmetric spaces that are necessary for our presentation in Sections 5, 6 and 7. For more details, readers may refer to [Reference Ballmann, Gromov and Schroeder1], [Reference Eberlein16] or [Reference Kapovich, Leeb and Porti26, Section 2.]
Throughout Sections 2.3 and 2.4, let G be a semisimple Lie group and X the associated symmetric space.
The visual boundary
![]() $\partial _{\infty } X$
of X has a topological spherical building structure, the Tits building associated to X. Let
$\partial _{\infty } X$
of X has a topological spherical building structure, the Tits building associated to X. Let
![]() $a_{\mathrm {mod}}$
denote the model apartment of this building and W the Weyl group acting isometrically on
$a_{\mathrm {mod}}$
denote the model apartment of this building and W the Weyl group acting isometrically on
![]() $a_{\mathrm {mod}}$
. We will fix a chamber
$a_{\mathrm {mod}}$
. We will fix a chamber
![]() ${\sigma _{\mathrm {mod}}}\subset a_{\mathrm {mod}}$
and call it the spherical model Weyl chamber; it is a fundamental domain for the W-action on
${\sigma _{\mathrm {mod}}}\subset a_{\mathrm {mod}}$
and call it the spherical model Weyl chamber; it is a fundamental domain for the W-action on
![]() $a_{\mathrm {mod}}$
. Let
$a_{\mathrm {mod}}$
. Let
![]() $w_0\in W$
denote the unique element sending
$w_0\in W$
denote the unique element sending
![]() ${\sigma _{\mathrm {mod}}}$
to the opposite chamber
${\sigma _{\mathrm {mod}}}$
to the opposite chamber
![]() $-{\sigma _{\mathrm {mod}}}$
. Then the opposition involution
$-{\sigma _{\mathrm {mod}}}$
. Then the opposition involution
![]() $\iota $
of the model chamber
$\iota $
of the model chamber
![]() ${\sigma _{\mathrm {mod}}}$
is defined as
${\sigma _{\mathrm {mod}}}$
is defined as
![]() $\iota =-w_0$
.
$\iota =-w_0$
.
We denote by
![]() $\Delta :=\Delta _{\mathrm {mod}}$
the model Weyl chamber corresponding to
$\Delta :=\Delta _{\mathrm {mod}}$
the model Weyl chamber corresponding to
![]() ${\sigma _{\mathrm {mod}}}$
, a fundamental domain for the W-action on the model (maximal) flat
${\sigma _{\mathrm {mod}}}$
, a fundamental domain for the W-action on the model (maximal) flat
![]() $F_{\mathrm {mod}}$
of X. We will use the notation
$F_{\mathrm {mod}}$
of X. We will use the notation
![]() $d_{\Delta }$
for the G-invariant
$d_{\Delta }$
for the G-invariant
![]() $\Delta $
-valued distance function on X.
$\Delta $
-valued distance function on X.
Consider the induced action of G on
![]() $\partial _{\infty } X$
. Every orbit intersects every chamber exactly once, so there is a natural identification
$\partial _{\infty } X$
. Every orbit intersects every chamber exactly once, so there is a natural identification
![]() $\partial _{\infty } X/G\cong {\sigma _{\mathrm {mod}}}$
. The projection
$\partial _{\infty } X/G\cong {\sigma _{\mathrm {mod}}}$
. The projection
![]() $\theta :\partial _{\infty } X\to \partial _{\infty } X/G$
is called the type map. Let
$\theta :\partial _{\infty } X\to \partial _{\infty } X/G$
is called the type map. Let
![]() ${\tau _{\mathrm {mod}}}$
be a face of
${\tau _{\mathrm {mod}}}$
be a face of
![]() ${\sigma _{\mathrm {mod}}}$
. We will assume, in what follows, that the simplex
${\sigma _{\mathrm {mod}}}$
. We will assume, in what follows, that the simplex
![]() ${\tau _{\mathrm {mod}}}$
is
${\tau _{\mathrm {mod}}}$
is
![]() $\iota $
-invariant. The
$\iota $
-invariant. The
![]() ${\tau _{\mathrm {mod}}}$
-flag manifold
${\tau _{\mathrm {mod}}}$
-flag manifold
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is the space of simplices of type
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is the space of simplices of type
![]() ${\tau _{\mathrm {mod}}}$
in
${\tau _{\mathrm {mod}}}$
in
![]() $\partial _{\infty } X$
. It has a structure of a compact smooth manifold and can be identified with the quotient space
$\partial _{\infty } X$
. It has a structure of a compact smooth manifold and can be identified with the quotient space
![]() $G/P_{\tau }$
, where
$G/P_{\tau }$
, where
![]() $P_{\tau }<G$
is the stabilizer subgroup of a simplex
$P_{\tau }<G$
is the stabilizer subgroup of a simplex
![]() $\tau \subset \partial _{\infty } X$
of type
$\tau \subset \partial _{\infty } X$
of type
![]() $\theta (\tau )={\tau _{\mathrm {mod}}}$
. Two simplices
$\theta (\tau )={\tau _{\mathrm {mod}}}$
. Two simplices
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
in
$\tau _2$
in
![]() $\partial _{\infty } X$
are said to be antipodal if they are opposite in an apartment containing both of them; their types are related by
$\partial _{\infty } X$
are said to be antipodal if they are opposite in an apartment containing both of them; their types are related by
![]() $\theta (\tau _2)=\iota \theta (\tau _1)$
. A subset E of
$\theta (\tau _2)=\iota \theta (\tau _1)$
. A subset E of
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is said to be antipodal if any two distinct elements of E are antipodal. A map into
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is said to be antipodal if any two distinct elements of E are antipodal. A map into
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is antipodal if it is injective and has an antipodal image. We shall always assume that
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is antipodal if it is injective and has an antipodal image. We shall always assume that
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is equipped with an auxiliary Riemannian metric.
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is equipped with an auxiliary Riemannian metric.
Let
![]() $\tau \subset \partial _{\infty } X$
be a simplex of type
$\tau \subset \partial _{\infty } X$
be a simplex of type
![]() ${\tau _{\mathrm {mod}}}$
. The star
${\tau _{\mathrm {mod}}}$
. The star
![]() $\mathrm {st}(\tau )\subset \partial _{\infty } X$
is the union of all chambers containing
$\mathrm {st}(\tau )\subset \partial _{\infty } X$
is the union of all chambers containing
![]() $\tau $
. We denote by
$\tau $
. We denote by
![]() $\partial \,\mathrm {st}(\tau )$
the union of all simplices in
$\partial \,\mathrm {st}(\tau )$
the union of all simplices in
![]() $\mathrm {st}(\tau )$
which do not contain
$\mathrm {st}(\tau )$
which do not contain
![]() $\tau $
, and define
$\tau $
, and define
![]() $\mathrm {ost}(\tau ):=\mathrm {st}(\tau )-\partial \,\mathrm {st}(\tau )$
. We denote by
$\mathrm {ost}(\tau ):=\mathrm {st}(\tau )-\partial \,\mathrm {st}(\tau )$
. We denote by
![]() $W_{{\tau _{\mathrm {mod}}}}$
the W-stabilizer of
$W_{{\tau _{\mathrm {mod}}}}$
the W-stabilizer of
![]() ${\tau _{\mathrm {mod}}}$
. A subset
${\tau _{\mathrm {mod}}}$
. A subset
![]() $\Theta \subset {\sigma _{\mathrm {mod}}}$
is
$\Theta \subset {\sigma _{\mathrm {mod}}}$
is
![]() $W_{\tau _{\mathrm {mod}}}$
-convex if its symmetrization
$W_{\tau _{\mathrm {mod}}}$
-convex if its symmetrization
![]() $W_{\tau _{\mathrm {mod}}}\Theta \subset a_{\mathrm {mod}}$
is convex; for such a subset
$W_{\tau _{\mathrm {mod}}}\Theta \subset a_{\mathrm {mod}}$
is convex; for such a subset
![]() $\Theta $
, we define
$\Theta $
, we define
![]() $\mathrm {st}_{\Theta }(\tau ):=\mathrm {st}(\tau )\cap \theta ^{-1}(\Theta )$
.
$\mathrm {st}_{\Theta }(\tau ):=\mathrm {st}(\tau )\cap \theta ^{-1}(\Theta )$
.
For
![]() $x\in X$
and
$x\in X$
and
![]() $S\subset \partial _{\infty } X$
, the Weyl cone
$S\subset \partial _{\infty } X$
, the Weyl cone
![]() $V(x,S)\subset X$
is defined to be the union of rays
$V(x,S)\subset X$
is defined to be the union of rays
![]() $x\xi $
(
$x\xi $
(
![]() $\xi \in S$
). For a flat
$\xi \in S$
). For a flat
![]() $f\subset X$
the parallel set,
$f\subset X$
the parallel set,
![]() $P(f)$
is the union of all flats
$P(f)$
is the union of all flats
![]() $f'$
such that
$f'$
such that
![]() $\partial _{\infty } f'=\partial _{\infty } f$
. For a pair of antipodal simplices
$\partial _{\infty } f'=\partial _{\infty } f$
. For a pair of antipodal simplices
![]() $\tau _1,\tau _2\subset \partial _{\infty } X$
, we define
$\tau _1,\tau _2\subset \partial _{\infty } X$
, we define
![]() $P(\tau _1,\tau _2)$
to be the parallel set of the unique minimal flat whose ideal boundary contains
$P(\tau _1,\tau _2)$
to be the parallel set of the unique minimal flat whose ideal boundary contains
![]() $\{\tau _1,\tau _2\}$
; equivalently, it is the union of all geodesics in X which are forward/backward asymptotic to points in
$\{\tau _1,\tau _2\}$
; equivalently, it is the union of all geodesics in X which are forward/backward asymptotic to points in
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
.
$\tau _2$
.
Definition 2.11 (Finsler geodesic)
A
![]() ${\tau _{\mathrm {mod}}}$
-Finsler geodesic is a continuous path
${\tau _{\mathrm {mod}}}$
-Finsler geodesic is a continuous path
![]() $c:I\to X$
contained in a parallel set
$c:I\to X$
contained in a parallel set
![]() $P(\tau _1,\tau _2)$
for
$P(\tau _1,\tau _2)$
for
![]() $\tau _1,\tau _2\in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that
$\tau _1,\tau _2\in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that
![]() $c(t_2)\in V(c(t_1),\mathrm {st}(\tau _2))$
for all subintervals
$c(t_2)\in V(c(t_1),\mathrm {st}(\tau _2))$
for all subintervals
![]() $[t_1,t_2]\subset I$
. It is uniformly
$[t_1,t_2]\subset I$
. It is uniformly
![]() ${\tau _{\mathrm {mod}}}$
-regular if
${\tau _{\mathrm {mod}}}$
-regular if
![]() $c(t_2)\in V(c(t_1),\mathrm {st}_{\Theta }(\tau _2))$
for some
$c(t_2)\in V(c(t_1),\mathrm {st}_{\Theta }(\tau _2))$
for some
![]() $W_{\tau _{\mathrm {mod}}}$
-convex compact subset
$W_{\tau _{\mathrm {mod}}}$
-convex compact subset
![]() $\Theta \subset \mathrm {int}_{\tau _{\mathrm {mod}}}({\sigma _{\mathrm {mod}}})$
.
$\Theta \subset \mathrm {int}_{\tau _{\mathrm {mod}}}({\sigma _{\mathrm {mod}}})$
.
Let
![]() $xy$
be a
$xy$
be a
![]() ${\tau _{\mathrm {mod}}}$
-regular oriented geodesic segment in X and
${\tau _{\mathrm {mod}}}$
-regular oriented geodesic segment in X and
![]() $x\xi $
the geodesic ray extending
$x\xi $
the geodesic ray extending
![]() $xy$
. We denote
$xy$
. We denote
![]() $\tau (xy)$
the unique simplex
$\tau (xy)$
the unique simplex
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that
![]() $\xi \in \mathrm {ost}(\tau )$
. Let
$\xi \in \mathrm {ost}(\tau )$
. Let
![]() $\Theta \subset \mathrm {int}_{\tau _{\mathrm {mod}}}({\sigma _{\mathrm {mod}}})$
. Then
$\Theta \subset \mathrm {int}_{\tau _{\mathrm {mod}}}({\sigma _{\mathrm {mod}}})$
. Then
![]() $xy$
is
$xy$
is
![]() $\Theta $
-regular if
$\Theta $
-regular if
![]() $\theta (\xi )\in \Theta $
. If
$\theta (\xi )\in \Theta $
. If
![]() $x_1x_2$
is
$x_1x_2$
is
![]() $\Theta $
-regular, we define its
$\Theta $
-regular, we define its
![]() $\Theta $
-diamond by
$\Theta $
-diamond by
Definition 2.12 (Morse quasi-geodesic)
A (discrete) quasi-geodesic
![]() $q:I\cap \mathbb {Z}\to X$
is
$q:I\cap \mathbb {Z}\to X$
is
![]() $(\Theta ,R)$
-Morse if for every subinterval
$(\Theta ,R)$
-Morse if for every subinterval
![]() $[t_1,t_2]\subset I$
the subpath
$[t_1,t_2]\subset I$
the subpath
![]() $q|_{[t_1,t_2]\cap \mathbb {Z}}$
is contained in the R-neighborhood of the diamond
$q|_{[t_1,t_2]\cap \mathbb {Z}}$
is contained in the R-neighborhood of the diamond
![]() $\Diamond _{\Theta }(x_1,x_2)$
such that
$\Diamond _{\Theta }(x_1,x_2)$
such that
![]() $d(x_i,q(t_i))\le R$
for
$d(x_i,q(t_i))\le R$
for
![]() $i=1,2$
.
$i=1,2$
.
It is shown in [Reference Kapovich, Leeb and Porti26, Theorem 5.53] that
![]() $(\Theta ,R)$
-Morse quasi-geodesic rays (resp. lines) are uniformly Hausdorff close to a uniformly
$(\Theta ,R)$
-Morse quasi-geodesic rays (resp. lines) are uniformly Hausdorff close to a uniformly
![]() ${\tau _{\mathrm {mod}}}$
-regular Finsler geodesic rays (resp. lines).
${\tau _{\mathrm {mod}}}$
-regular Finsler geodesic rays (resp. lines).
2.4 Anosov subgroups
We recall the definitions of Anosov and nonuniformly Anosov subgroups given by Kapovich, Leeb and Porti in [Reference Kapovich, Leeb and Porti26, Definitions 5.43 and 5.62]. Many other equivalent characterizations of the Anosov subgroups are established in [Reference Kapovich, Leeb and Porti26, Theorem 5.47], and their equivalence with the original definitions given by Labourie [Reference Labourie28] and Guichard and Wienhard [Reference Guichard and Wienhard19] is proven in [Reference Kapovich, Leeb and Porti26, Section 5.11].
Definition 2.13. Let
![]() ${\tau _{\mathrm {mod}}}\subset {\sigma _{\mathrm {mod}}}$
be an
${\tau _{\mathrm {mod}}}\subset {\sigma _{\mathrm {mod}}}$
be an
![]() $\iota $
-invariant face. A subgroup
$\iota $
-invariant face. A subgroup
![]() $\Gamma $
of a semisimple Lie group G is
$\Gamma $
of a semisimple Lie group G is
![]() ${\tau _{\mathrm {mod}}}$
-boundary embedded if
${\tau _{\mathrm {mod}}}$
-boundary embedded if
-
(a) it is a hyperbolic group;
-
(b) there is an antipodal
 $\Gamma $
-equivariant continuous map (called a boundary embedding)
$\Gamma $
-equivariant continuous map (called a boundary embedding)  $$\begin{align*}\psi:\partial_{\infty}\Gamma\to\mathrm{Flag}({\tau_{\mathrm{mod}}}). \end{align*}$$
$$\begin{align*}\psi:\partial_{\infty}\Gamma\to\mathrm{Flag}({\tau_{\mathrm{mod}}}). \end{align*}$$
A
![]() ${\tau _{\mathrm {mod}}}$
-boundary embedded subgroup
${\tau _{\mathrm {mod}}}$
-boundary embedded subgroup
![]() $\Gamma <G$
with a boundary embedding
$\Gamma <G$
with a boundary embedding
![]() $\psi $
is
$\psi $
is
![]() ${\tau _{\mathrm {mod}}}$
-Anosov if
${\tau _{\mathrm {mod}}}$
-Anosov if
-
(c) for every
 $\xi \in \partial _{\infty }\Gamma $
and for every geodesic ray
$\xi \in \partial _{\infty }\Gamma $
and for every geodesic ray
 $r:\mathbb {N}_0\to \Gamma $
starting at
$r:\mathbb {N}_0\to \Gamma $
starting at
 $e\in \Gamma $
and asymptotic to
$e\in \Gamma $
and asymptotic to
 $\xi $
, the expansion factor (see equation (2.2)) satisfies
$\xi $
, the expansion factor (see equation (2.2)) satisfies  $$ \begin{align*} \mathcal E(r(k)^{-1},\psi(\xi))\ge A\, e^{C k} \end{align*} $$
$$ \begin{align*} \mathcal E(r(k)^{-1},\psi(\xi))\ge A\, e^{C k} \end{align*} $$
for
 $k\in \mathbb {N}_0$
with constants
$k\in \mathbb {N}_0$
with constants
 $A,C>0$
independent of the point
$A,C>0$
independent of the point
 $\xi $
and the ray r.
$\xi $
and the ray r.
A
![]() ${\tau _{\mathrm {mod}}}$
-boundary embedded subgroup
${\tau _{\mathrm {mod}}}$
-boundary embedded subgroup
![]() $\Gamma <G$
with a boundary embedding
$\Gamma <G$
with a boundary embedding
![]() $\psi $
is nonuniformly
$\psi $
is nonuniformly
![]() ${\tau _{\mathrm {mod}}}$
-Anosov if
${\tau _{\mathrm {mod}}}$
-Anosov if
-
(d) for every
 $\xi \in \partial _{\infty }\Gamma $
and for every geodesic ray
$\xi \in \partial _{\infty }\Gamma $
and for every geodesic ray
 $r:\mathbb {N}_0\to \Gamma $
starting at
$r:\mathbb {N}_0\to \Gamma $
starting at
 $e\in \Gamma $
and asymptotic to
$e\in \Gamma $
and asymptotic to
 $\xi $
, the expansion factor satisfies
$\xi $
, the expansion factor satisfies  $$ \begin{align*} \sup_{k\in\mathbb{N}_0}\,\mathcal E(r(k)^{-1},\psi(\xi))=+\infty. \end{align*} $$
$$ \begin{align*} \sup_{k\in\mathbb{N}_0}\,\mathcal E(r(k)^{-1},\psi(\xi))=+\infty. \end{align*} $$
A
![]() ${\tau _{\mathrm {mod}}}$
-boundary embedded subgroup
${\tau _{\mathrm {mod}}}$
-boundary embedded subgroup
![]() $\Gamma <G$
is said to be nonelementary if it is a nonelementary hyperbolic group.
$\Gamma <G$
is said to be nonelementary if it is a nonelementary hyperbolic group.
Remark 2.14.
-
(a) In fact, for
 ${\tau _{\mathrm {mod}}}$
-boundary embedded subgroups, the conditions (c) and (d) are equivalent; see [Reference Kapovich, Leeb and Porti26, Theorem 5.47]. For the purpose of this paper, the definition of nonuniformly
${\tau _{\mathrm {mod}}}$
-boundary embedded subgroups, the conditions (c) and (d) are equivalent; see [Reference Kapovich, Leeb and Porti26, Theorem 5.47]. For the purpose of this paper, the definition of nonuniformly
 ${\tau _{\mathrm {mod}}}$
-Anosov subgroups will suffice.
${\tau _{\mathrm {mod}}}$
-Anosov subgroups will suffice. -
(b) A
 ${\tau _{\mathrm {mod}}}$
-Anosov subgroup
${\tau _{\mathrm {mod}}}$
-Anosov subgroup
 $\Gamma <G$
may have other boundary embeddings
$\Gamma <G$
may have other boundary embeddings
 $\varphi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})$
besides the map
$\varphi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})$
besides the map
 $\psi $
which appears in the definition; see [Reference Kapovich, Leeb and Porti24, Example 6.20]. However, the boundary embedding
$\psi $
which appears in the definition; see [Reference Kapovich, Leeb and Porti24, Example 6.20]. However, the boundary embedding
 $\psi $
as in the conditions (c) and (d) is unique; its image is the
$\psi $
as in the conditions (c) and (d) is unique; its image is the
 ${\tau _{\mathrm {mod}}}$
-limit set of
${\tau _{\mathrm {mod}}}$
-limit set of
 $\Gamma $
in
$\Gamma $
in
 $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
,
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
,  $$\begin{align*}\psi(\partial_{\infty}\Gamma)= \Lambda_{\Gamma}({\tau_{\mathrm{mod}}})\subset\mathrm{Flag}({\tau_{\mathrm{mod}}}). \end{align*}$$
$$\begin{align*}\psi(\partial_{\infty}\Gamma)= \Lambda_{\Gamma}({\tau_{\mathrm{mod}}})\subset\mathrm{Flag}({\tau_{\mathrm{mod}}}). \end{align*}$$
We thus will refer to the map
 $\psi $
as the asymptotic embedding for
$\psi $
as the asymptotic embedding for
 $\Gamma < G$
.
$\Gamma < G$
.
3 Expansion and meandering hyperbolicity
Throughout Sections 3 and 4, we let
![]() $(M,d)$
be a proper geodesic metric space and suppose that a discrete group
$(M,d)$
be a proper geodesic metric space and suppose that a discrete group
![]() $\Gamma $
acts continuously on M with a nonempty invariant compact subset
$\Gamma $
acts continuously on M with a nonempty invariant compact subset
![]() $\Lambda \subset M$
, no point of which is isolated in M.
$\Lambda \subset M$
, no point of which is isolated in M.
Remark 3.1. Note that we do not assume faithfulness of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
and even on M.
$\Lambda $
and even on M.
In this situation, one considers two conditions on
![]() $\rho $
called the expansion and meandering hyperbolicity conditions, respectively. The meandering hyperbolicity condition will require the expansion condition.
$\rho $
called the expansion and meandering hyperbolicity conditions, respectively. The meandering hyperbolicity condition will require the expansion condition.
In the present section, we define the expansion condition, and draw the key Lemma 3.14 as well as its various consequences (Sections 3.1 and 3.3). We then define the meandering hyperbolicity condition (Section 3.4).
3.1 The expansion condition
In order to define the expansion condition we need a little preparation.
Let f be a homeomorphism of M. Given
![]() $\lambda>1$
and
$\lambda>1$
and
![]() $U\subset M$
, we say f is
$U\subset M$
, we say f is
![]() $(\lambda ,U)$
-expanding (or
$(\lambda ,U)$
-expanding (or
![]() $\lambda $
-expanding on U) if
$\lambda $
-expanding on U) if
for all
![]() $x,y\in U$
. In this case, we also say U is a
$x,y\in U$
. In this case, we also say U is a
![]() $(\lambda ,f)$
-expanding subset. Note that f is
$(\lambda ,f)$
-expanding subset. Note that f is
![]() $(\lambda ,U)$
-expanding if and only if
$(\lambda ,U)$
-expanding if and only if
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $(\lambda ^{-1},f(U))$
-contracting, that is,
$(\lambda ^{-1},f(U))$
-contracting, that is,
for all
![]() $x,y\in f(U)$
.
$x,y\in f(U)$
.
Given
![]() $\delta>0$
, a
$\delta>0$
, a
![]() $(\lambda ,U)$
-expanding homeomorphism f is said to be
$(\lambda ,U)$
-expanding homeomorphism f is said to be
![]() $(\lambda ,U;\delta )$
-expanding if
$(\lambda ,U;\delta )$
-expanding if
Clearly, if f is
![]() $(\lambda ,U;\delta )$
-expanding, then it is also
$(\lambda ,U;\delta )$
-expanding, then it is also
![]() $(\lambda ,U;\delta ')$
-expanding for every
$(\lambda ,U;\delta ')$
-expanding for every
![]() $\delta '\le \delta $
.
$\delta '\le \delta $
.
Lemma 3.2. If M is a geodesic metric space, then every
![]() $(\lambda ,U)$
-expanding homeomorphism is also
$(\lambda ,U)$
-expanding homeomorphism is also
![]() $(\lambda ,U;\delta )$
-expanding for every
$(\lambda ,U;\delta )$
-expanding for every
![]() $\delta $
.
$\delta $
.
Proof. Suppose to the contrary that there exists a point
Let c be a geodesic path in M connecting
![]() $f(x)$
and y; the length of this geodesic is less than
$f(x)$
and y; the length of this geodesic is less than
![]() $\lambda \eta $
. Since
$\lambda \eta $
. Since
![]() $f(B_{\eta }(x))$
is open in M, the path c crosses the boundary of
$f(B_{\eta }(x))$
is open in M, the path c crosses the boundary of
![]() $f(B_{\eta }(x))$
at a point z. Because f is
$f(B_{\eta }(x))$
at a point z. Because f is
![]() $\lambda $
-expanding on the set U containing
$\lambda $
-expanding on the set U containing
![]() $B_{\eta }(x)$
and
$B_{\eta }(x)$
and
![]() $f^{-1}(z)\in \partial B_{\eta }(x)$
, we have
$f^{-1}(z)\in \partial B_{\eta }(x)$
, we have
This contradicts the assumption that
![]() $y\in B_{\lambda \eta }(f(x))$
, that is,
$y\in B_{\lambda \eta }(f(x))$
, that is,
![]() $d(f(x), y)< \lambda \eta $
.
$d(f(x), y)< \lambda \eta $
.
The implication in the lemma does not hold for general metric spaces. As a simple example, consider a compact metric space M of diameter D, which is not a singleton, but contains an isolated point x. Consider
![]() $f=\mathrm {Id}_M$
and take a neighborhood U of x and
$f=\mathrm {Id}_M$
and take a neighborhood U of x and
![]() $\eta>0$
such that
$\eta>0$
such that
![]() $\{x\}=B_{\eta }(x)\subset U=\{x\}$
. Then f is
$\{x\}=B_{\eta }(x)\subset U=\{x\}$
. Then f is
![]() $(\lambda ,U)$
-expanding for any
$(\lambda ,U)$
-expanding for any
![]() $\lambda>1$
. Thus, taking
$\lambda>1$
. Thus, taking
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda \eta \ge D$
, we see that
$\lambda \eta \ge D$
, we see that
However, we note the following fact:
Lemma 3.3. Suppose that f is
![]() $(\lambda ,U)$
-expanding, where U is a bounded open subset of M. Then for every
$(\lambda ,U)$
-expanding, where U is a bounded open subset of M. Then for every
![]() $\delta>0$
there exists
$\delta>0$
there exists
![]() $\delta '= \delta ^{\prime }_U>0$
such that f is
$\delta '= \delta ^{\prime }_U>0$
such that f is
![]() $(\lambda ,U';\delta ')$
-expanding with
$(\lambda ,U';\delta ')$
-expanding with
![]() $U':=\mathrm {int}\, U^{\delta } \subset U$
.
$U':=\mathrm {int}\, U^{\delta } \subset U$
.
Proof. Since
![]() $f(U^{\delta })$
is compact, we have
$f(U^{\delta })$
is compact, we have
![]() $\epsilon :=d(f(U^{\delta }), M-f(U))>0$
. Now, we let
$\epsilon :=d(f(U^{\delta }), M-f(U))>0$
. Now, we let
![]() $\delta ':=\lambda ^{-1}\cdot \min \{\delta ,\epsilon \}$
. If
$\delta ':=\lambda ^{-1}\cdot \min \{\delta ,\epsilon \}$
. If
![]() $\eta \le \delta '$
and
$\eta \le \delta '$
and
![]() $B_{\eta }(x)\subset U'$
, in particular,
$B_{\eta }(x)\subset U'$
, in particular,
![]() $f(x)\in f(U^{\delta })$
, then we have
$f(x)\in f(U^{\delta })$
, then we have
![]() $B_{\lambda \eta }(f(x))\subset B_{\epsilon }(f(x))\subset f(U)$
and hence
$B_{\lambda \eta }(f(x))\subset B_{\epsilon }(f(x))\subset f(U)$
and hence
![]() $f^{-1}[B_{\lambda \eta }(f(x))]\subset B_{\eta }(x)$
since
$f^{-1}[B_{\lambda \eta }(f(x))]\subset B_{\eta }(x)$
since
![]() $f^{-1}$
is
$f^{-1}$
is
![]() $(1/\lambda ,f(U))$
-contracting. Therefore, we conclude that
$(1/\lambda ,f(U))$
-contracting. Therefore, we conclude that
![]() $B_{\lambda \eta }(f(x))\subset f(B_{\eta }(x))$
.
$B_{\lambda \eta }(f(x))\subset f(B_{\eta }(x))$
.
We are now ready to define the expansion condition. Let
![]() $\mathrm {LHomeo}(M)$
denote the group of locally bi-Lipschitz homeomorphisms of M, that is, homeomorphisms of M whose restrictions to compact subsets are bi-Lipschitz.
$\mathrm {LHomeo}(M)$
denote the group of locally bi-Lipschitz homeomorphisms of M, that is, homeomorphisms of M whose restrictions to compact subsets are bi-Lipschitz.
Definition 3.4 (Expansion)
Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be an action with a nonempty compact invariant subset
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be an action with a nonempty compact invariant subset
![]() $\Lambda $
, no point of which is isolated in M. The action
$\Lambda $
, no point of which is isolated in M. The action
![]() $\rho $
is said to be expanding at
$\rho $
is said to be expanding at
![]() $\Lambda $
if there exist
$\Lambda $
if there exist
-
• a finite index set
 $\mathcal {I}$
,
$\mathcal {I}$
, -
• a cover
 $\mathcal {U}=\{U_i\subset M \mid i\in \mathcal {I}\}$
of
$\mathcal {U}=\{U_i\subset M \mid i\in \mathcal {I}\}$
of
 $\Lambda $
by open (and possibly empty) subsets
$\Lambda $
by open (and possibly empty) subsets
 $U_i$
,
$U_i$
, -
• a map
 $s:\mathcal {I}\to \Gamma $
,
$s:\mathcal {I}\to \Gamma $
,
 $i\mapsto s_i$
,
$i\mapsto s_i$
, -
• and positive real numbers
 $L\ge \lambda>1$
and
$L\ge \lambda>1$
and
 $\delta \le \delta _{\mathcal {U}}$
$\delta \le \delta _{\mathcal {U}}$
such that, for every
![]() $i\in \mathcal {I}$
, the map
$i\in \mathcal {I}$
, the map
![]() $\rho (s_i^{-1})$
is
$\rho (s_i^{-1})$
is
-
(i) L-Lipschitz on
 $N_{\delta }(\Lambda )$
, and
$N_{\delta }(\Lambda )$
, and -
(ii)
 $(\lambda ,U_{\alpha };\delta )$
-expanding,
$(\lambda ,U_{\alpha };\delta )$
-expanding,
and that the image
![]() $\varSigma :=\{s_i \mid i\in \mathcal {I}\}\subset \Gamma $
of the map s is a symmetric generating set of the group
$\varSigma :=\{s_i \mid i\in \mathcal {I}\}\subset \Gamma $
of the map s is a symmetric generating set of the group
![]() $\Gamma $
.
$\Gamma $
.
In this case, the datum
![]() $\mathcal {D}:=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
(or, occasionally, any subset thereof) will be referred to as an expansion datum of
$\mathcal {D}:=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
(or, occasionally, any subset thereof) will be referred to as an expansion datum of
![]() $\rho $
.
$\rho $
.
If
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is an expanding action, let
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is an expanding action, let
![]() $|\cdot |_{\varSigma }$
(resp.
$|\cdot |_{\varSigma }$
(resp.
![]() $d_{\varSigma }$
) denote the word length (resp. the word metric) on the group
$d_{\varSigma }$
) denote the word length (resp. the word metric) on the group
![]() $\Gamma $
with respect to the generating set
$\Gamma $
with respect to the generating set
![]() $\varSigma $
from Definition 3.4. Then the L-Lipschitz property (i) implies that
$\varSigma $
from Definition 3.4. Then the L-Lipschitz property (i) implies that
for every
![]() $g\in \Gamma $
with
$g\in \Gamma $
with
![]() $|g|_{\varSigma }=k\in \mathbb {N}$
.
$|g|_{\varSigma }=k\in \mathbb {N}$
.
Remark 3.6. A few more remarks are in order.
-
(a) Expanding actions appear naturally in the context of Anosov actions on flag manifolds [Reference Kapovich, Leeb and Porti26, Definition 3.1] and hyperbolic group actions on their Gromov boundaries equipped with visual metrics [Reference Coornaert10]. See Section 6 for further discussion.
-
(b) The symmetry of the generating set
 $\varSigma $
means that
$\varSigma $
means that
 $s\in \varSigma $
if and only if
$s\in \varSigma $
if and only if
 $s^{-1}\in \varSigma $
. This implies that
$s^{-1}\in \varSigma $
. This implies that
 $\rho (s_i)$
is L-bi-Lipschitz on
$\rho (s_i)$
is L-bi-Lipschitz on
 $N_{\delta /L}(\Lambda )$
for all
$N_{\delta /L}(\Lambda )$
for all
 $i\in \mathcal {I}$
.
$i\in \mathcal {I}$
. -
(c) Suppose that M is a Riemannian manifold and the action
 $\rho $
is by
$\rho $
is by
 $C^1$
-diffeomorphisms. Then,
$C^1$
-diffeomorphisms. Then,
 $\rho $
is expanding provided that for every
$\rho $
is expanding provided that for every
 $x\in \Lambda $
there exists
$x\in \Lambda $
there exists
 $g\in \Gamma $
such that
$g\in \Gamma $
such that
 $\mathcal E(\rho (g),x)>1$
(see equation (2.2)). Indeed, by compactness of
$\mathcal E(\rho (g),x)>1$
(see equation (2.2)). Indeed, by compactness of
 $\Lambda $
, there exists a finite cover
$\Lambda $
, there exists a finite cover
 $\mathcal {U}=\{U_i \mid i\in \mathcal {I}\}$
of
$\mathcal {U}=\{U_i \mid i\in \mathcal {I}\}$
of
 $\Lambda $
and a collection
$\Lambda $
and a collection
 $\varSigma $
of group elements
$\varSigma $
of group elements
 $s_i\in \Gamma $
such that each
$s_i\in \Gamma $
such that each
 $\rho (s_i^{-1})$
is
$\rho (s_i^{-1})$
is
 $(\lambda ,U_i;\delta _{\mathcal {U}})$
-expanding. By adding, if necessary, extra generators to
$(\lambda ,U_i;\delta _{\mathcal {U}})$
-expanding. By adding, if necessary, extra generators to
 $\varSigma $
with empty expanding subsets, we obtain the required symmetric generating set of
$\varSigma $
with empty expanding subsets, we obtain the required symmetric generating set of
 $\Gamma $
.
$\Gamma $
. -
(d) If
 $U_i=\emptyset $
for some
$U_i=\emptyset $
for some
 $i\in \mathcal {I}$
then the condition (ii) is vacuous for this i. Otherwise, it implies that the inverse
$i\in \mathcal {I}$
then the condition (ii) is vacuous for this i. Otherwise, it implies that the inverse
 $\rho (s_i)$
is
$\rho (s_i)$
is
 $(\lambda ^{-1},\rho (s_i^{-1})[U_i])$
-contracting.
$(\lambda ^{-1},\rho (s_i^{-1})[U_i])$
-contracting. -
(e) The condition (ii) can be relaxed to the mere
 $(\lambda ,U_i)$
-expanding condition. Namely, we may first modify the cover
$(\lambda ,U_i)$
-expanding condition. Namely, we may first modify the cover
 $\mathcal {U}=\{U_i\mid i \in \mathcal {I}\}$
so that
$\mathcal {U}=\{U_i\mid i \in \mathcal {I}\}$
so that
 $U_i$
are all bounded. Then, in view of Lemma 3.3, we can modify it further to
$U_i$
are all bounded. Then, in view of Lemma 3.3, we can modify it further to
 $\mathcal {U}'=\{U^{\prime }_i \mid i \in \mathcal {I} \}$
, where
$\mathcal {U}'=\{U^{\prime }_i \mid i \in \mathcal {I} \}$
, where
 $U^{\prime }_i:=\mathrm {int}\, U^{\delta }_i$
as in the lemma. For each
$U^{\prime }_i:=\mathrm {int}\, U^{\delta }_i$
as in the lemma. For each
 $i\in \mathcal {I}$
, we also let
$i\in \mathcal {I}$
, we also let
 $\delta ^{\prime }_{U_i}$
denote the number
$\delta ^{\prime }_{U_i}$
denote the number
 $\delta ^{\prime }_{U}$
given by the lemma, and set
$\delta ^{\prime }_{U}$
given by the lemma, and set  $$\begin{align*}\delta':= \min\{\delta_{\mathcal{U}'},\delta^{\prime}_{U_i}\mid i\in\mathcal{I}\}. \end{align*}$$
$$\begin{align*}\delta':= \min\{\delta_{\mathcal{U}'},\delta^{\prime}_{U_i}\mid i\in\mathcal{I}\}. \end{align*}$$
After such modification
 $\mathcal {U}'$
is still an open cover of
$\mathcal {U}'$
is still an open cover of
 $\Lambda $
and the maps
$\Lambda $
and the maps
 $\rho (s_i^{-1})$
are
$\rho (s_i^{-1})$
are
 $(\lambda ,U^{\prime }_i;\delta ')$
-expanding.
$(\lambda ,U^{\prime }_i;\delta ')$
-expanding. -
(f) The map
 $s:\mathcal {I}\to \varSigma \subset \Gamma $
is not necessarily injective: The
$s:\mathcal {I}\to \varSigma \subset \Gamma $
is not necessarily injective: The
 $\rho $
-image of an element of
$\rho $
-image of an element of
 $\Gamma $
can have several expansion subsets. See Examples 3.9, 7.3 and 7.4.
$\Gamma $
can have several expansion subsets. See Examples 3.9, 7.3 and 7.4. -
(g) Clearly, the properties (i) and (ii) also hold on the closures
 $\overline {N}_{\delta }(\Lambda )$
and
$\overline {N}_{\delta }(\Lambda )$
and
 $\overline {U_i}$
, respectively.
$\overline {U_i}$
, respectively.
It is possible that an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding with different expansion data. In such a case, we define a relation on the expansion data as follows.
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding with different expansion data. In such a case, we define a relation on the expansion data as follows.
Definition 3.7. Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mathcal {D}_0=(\mathcal {I}_0,\mathcal {U}_0,\varSigma _0, \delta _0,L_0,\lambda _0)$
and
$\mathcal {D}_0=(\mathcal {I}_0,\mathcal {U}_0,\varSigma _0, \delta _0,L_0,\lambda _0)$
and
![]() $\mathcal {D}_1=(\mathcal {I}_1,\mathcal {U}_1,\varSigma _1, \delta _1,L_1,\lambda _1)$
be its expansion data, where
$\mathcal {D}_1=(\mathcal {I}_1,\mathcal {U}_1,\varSigma _1, \delta _1,L_1,\lambda _1)$
be its expansion data, where
![]() $\mathcal {U}_k=\{U_{k,i} \mid i\in \mathcal {I}_k\}$
and
$\mathcal {U}_k=\{U_{k,i} \mid i\in \mathcal {I}_k\}$
and
![]() $\varSigma _k=\{s_{k,i} \mid i\in \mathcal {I}_k\}$
for
$\varSigma _k=\{s_{k,i} \mid i\in \mathcal {I}_k\}$
for
![]() $k=0,1$
. We write
$k=0,1$
. We write
![]() $\mathcal {U}_0 \prec \mathcal {U}_1$
(resp.
$\mathcal {U}_0 \prec \mathcal {U}_1$
(resp.
![]() $\varSigma _0 \prec \varSigma _1$
) if
$\varSigma _0 \prec \varSigma _1$
) if
![]() $\mathcal {I}_0\subset \mathcal {I}_1$
and
$\mathcal {I}_0\subset \mathcal {I}_1$
and
![]() $U_{0,i} \subset U_{1,i}$
(resp.
$U_{0,i} \subset U_{1,i}$
(resp.
![]() $s_{0,i}=s_{1,i}$
) for every
$s_{0,i}=s_{1,i}$
) for every
![]() $i\in \mathcal {I}_0$
. Furthermore, we write
$i\in \mathcal {I}_0$
. Furthermore, we write
![]() $\mathcal {D}_0\prec \mathcal {D}_1$
and say
$\mathcal {D}_0\prec \mathcal {D}_1$
and say
![]() $\mathcal {D}_1$
is a refinement of
$\mathcal {D}_1$
is a refinement of
![]() $\mathcal {D}_0$
if
$\mathcal {D}_0$
if
Note the strict inequality
![]() $\delta _0>\delta _1$
, which will be pertinent to Section 4.6.
$\delta _0>\delta _1$
, which will be pertinent to Section 4.6.
Definition 3.8. For any expansion datum
![]() $\mathcal {D}$
, we can define a refinement by replacing
$\mathcal {D}$
, we can define a refinement by replacing
![]() $\delta $
with a strictly smaller positive number and leaving other objects intact. We say such a refinement is trivial.
$\delta $
with a strictly smaller positive number and leaving other objects intact. We say such a refinement is trivial.
3.2 Toy examples of expanding actions
The most basic example of an expanding action is a cyclic hyperbolic group of Möbius transformations acting on the unit circle
![]() $S^1$
. Namely, we consider the Poincaré (conformal) disk model of
$S^1$
. Namely, we consider the Poincaré (conformal) disk model of
![]() $\mathbb {H}^2$
in
$\mathbb {H}^2$
in
![]() $\mathbb {C}=\mathbb {R}^2$
and endow
$\mathbb {C}=\mathbb {R}^2$
and endow
![]() $M=S^1=\partial _{\infty }\mathbb {H}^2$
with the induced Euclidean metric. Let
$M=S^1=\partial _{\infty }\mathbb {H}^2$
with the induced Euclidean metric. Let
![]() $\gamma \in \mathrm {Isom}(\mathbb {H}^2)$
be a hyperbolic element and
$\gamma \in \mathrm {Isom}(\mathbb {H}^2)$
be a hyperbolic element and
![]() $\Gamma = \langle \gamma \rangle \cong \mathbb {Z}$
. The limit set of the group
$\Gamma = \langle \gamma \rangle \cong \mathbb {Z}$
. The limit set of the group
![]() $\Gamma $
is
$\Gamma $
is
![]() $\Lambda =\{\gamma _-, \gamma _+\}$
, with
$\Lambda =\{\gamma _-, \gamma _+\}$
, with
![]() $\gamma _+$
the attracting and
$\gamma _+$
the attracting and
![]() $\gamma _-$
the repelling fixed points of
$\gamma _-$
the repelling fixed points of
![]() $\gamma $
in M. Expanding subsets
$\gamma $
in M. Expanding subsets
![]() $U_{\alpha }, U_{\beta }$
for
$U_{\alpha }, U_{\beta }$
for
![]() $\gamma , \gamma ^{-1}$
are sufficiently small arcs containing
$\gamma , \gamma ^{-1}$
are sufficiently small arcs containing
![]() $\gamma _-, \gamma _+$
, respectively.
$\gamma _-, \gamma _+$
, respectively.
Explicit expanding subsets can be found by considering the isometric circles
![]() $I_{\gamma }$
and
$I_{\gamma }$
and
![]() $I_{\gamma ^{-1}}$
of
$I_{\gamma ^{-1}}$
of
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^{-1}$
, respectively. See Figure 1(Left). (For the definition of isometric circles (or spheres) and their relation to Ford and Dirichlet fundamental domains, we refer to [Reference Maskit31, IV.G].) The arc of
$\gamma ^{-1}$
, respectively. See Figure 1(Left). (For the definition of isometric circles (or spheres) and their relation to Ford and Dirichlet fundamental domains, we refer to [Reference Maskit31, IV.G].) The arc of
![]() $I_{\gamma }$
in
$I_{\gamma }$
in
![]() $\mathbb {H}^2$
is a complete geodesic which is the perpendicular bisector of the points o and
$\mathbb {H}^2$
is a complete geodesic which is the perpendicular bisector of the points o and
![]() $\gamma ^{-1}(o)$
, where o denotes the Euclidean center of the Poincaré disk. Then we obtain a
$\gamma ^{-1}(o)$
, where o denotes the Euclidean center of the Poincaré disk. Then we obtain a
![]() $(\lambda ,\gamma )$
-expanding subset
$(\lambda ,\gamma )$
-expanding subset
![]() $U_{\alpha }$
(with
$U_{\alpha }$
(with
![]() $\lambda>1$
) by cutting down slightly the open arc of
$\lambda>1$
) by cutting down slightly the open arc of
![]() $S^1=\partial _{\infty }\mathbb {H}^2$
inside
$S^1=\partial _{\infty }\mathbb {H}^2$
inside
![]() $I_{\gamma }$
. See also the discussion in the beginning of Section 7.2.
$I_{\gamma }$
. See also the discussion in the beginning of Section 7.2.

Figure 1 Expanding arcs for
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^{-1}$
are colored gray in both examples. (Left) A hyperbolic transformation
$\gamma ^{-1}$
are colored gray in both examples. (Left) A hyperbolic transformation
![]() $\gamma $
of
$\gamma $
of
![]() $\mathbb {H}^2$
. (Right) A covering of degree
$\mathbb {H}^2$
. (Right) A covering of degree
![]() $3$
.
$3$
.
Example 3.9 (k-fold nontrivial covering)
A more interesting example is obtained by taking a degree
![]() $k>1$
covering
$k>1$
covering
![]() $p: S^1\to S^1$
of the preceding example. See Figure 1(Right) for the case of
$p: S^1\to S^1$
of the preceding example. See Figure 1(Right) for the case of
![]() $k=3$
. The preimage of
$k=3$
. The preimage of
![]() $\Lambda =\{\gamma _-, \gamma _+\}$
consists of
$\Lambda =\{\gamma _-, \gamma _+\}$
consists of
![]() $2k$
points, and we can lift
$2k$
points, and we can lift
![]() $\gamma $
to a diffeomorphism
$\gamma $
to a diffeomorphism
![]() $\widetilde \gamma : S^1\to S^1$
fixing all these points. Let
$\widetilde \gamma : S^1\to S^1$
fixing all these points. Let
![]() $\widetilde \rho : \Gamma =\langle \gamma \rangle \cong \mathbb {Z}\to \mathrm {Diff}(S^1)$
be the homomorphism sending the generator
$\widetilde \rho : \Gamma =\langle \gamma \rangle \cong \mathbb {Z}\to \mathrm {Diff}(S^1)$
be the homomorphism sending the generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma $
to
$\Gamma $
to
![]() $\widetilde \gamma $
. The preimages
$\widetilde \gamma $
. The preimages
![]() $p^{-1}(U_{\alpha })$
,
$p^{-1}(U_{\alpha })$
,
![]() $p^{-1}(U_{\beta })$
break into connected components
$p^{-1}(U_{\beta })$
break into connected components
and the mappings
![]() $\widetilde \gamma $
and
$\widetilde \gamma $
and
![]() $\widetilde \gamma ^{-1}$
act as expanding maps on each of these components. Therefore, we set
$\widetilde \gamma ^{-1}$
act as expanding maps on each of these components. Therefore, we set
and define the map
![]() $s:\mathcal {I}\to \varSigma $
,
$s:\mathcal {I}\to \varSigma $
,
from this index set to the generating set
![]() $\varSigma =\{\gamma , \gamma ^{-1}\}$
of
$\varSigma =\{\gamma , \gamma ^{-1}\}$
of
![]() $\Gamma $
. Then
$\Gamma $
. Then
![]() $\widetilde {U}_{\alpha _i}$
,
$\widetilde {U}_{\alpha _i}$
,
![]() $\widetilde {U}_{\beta _i}$
will be expanding subsets for the actions
$\widetilde {U}_{\beta _i}$
will be expanding subsets for the actions
![]() $\widetilde \rho (s_{\alpha _i})$
,
$\widetilde \rho (s_{\alpha _i})$
,
![]() $\widetilde \rho (s_{\beta _i})$
on
$\widetilde \rho (s_{\beta _i})$
on
![]() $S^1$
. (Note that the entire preimage
$S^1$
. (Note that the entire preimage
![]() $p^{-1}(U_{\alpha })$
(resp.
$p^{-1}(U_{\alpha })$
(resp.
![]() $p^{-1}(U_{\beta })$
) is not an expanding subset for the action
$p^{-1}(U_{\beta })$
) is not an expanding subset for the action
![]() $\widetilde \rho (s_{\alpha _i})$
(resp.
$\widetilde \rho (s_{\alpha _i})$
(resp.
![]() $\widetilde \rho (s_{\beta _i})$
).)
$\widetilde \rho (s_{\beta _i})$
).)
The same construction works for surface group actions; see Example 7.3.
A trivial example where
![]() $U_i=\emptyset $
for an index
$U_i=\emptyset $
for an index
![]() $i\in \mathcal {I}$
is the action of a cyclic group
$i\in \mathcal {I}$
is the action of a cyclic group
![]() $\Gamma = \langle \gamma \rangle \cong \mathbb {Z}$
generated by a loxodromic transformation
$\Gamma = \langle \gamma \rangle \cong \mathbb {Z}$
generated by a loxodromic transformation
![]() $\gamma (z)=mz$
,
$\gamma (z)=mz$
,
![]() $|m|>1$
, on
$|m|>1$
, on
![]() $M=\mathbb {C}$
(with the standard Euclidean metric) and
$M=\mathbb {C}$
(with the standard Euclidean metric) and
![]() $\Lambda =\{0\}$
. Any open subset of M containing
$\Lambda =\{0\}$
. Any open subset of M containing
![]() $0$
is an expanding subset for
$0$
is an expanding subset for
![]() $\gamma $
, while the expanding subset for
$\gamma $
, while the expanding subset for
![]() $\gamma ^{-1}$
is empty.
$\gamma ^{-1}$
is empty.
3.3 Expansion enables encoding
Given an expanding action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
with an invariant subset
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
with an invariant subset
![]() $\Lambda $
the expansion condition (Definition 3.4) enables us to encode points of
$\Lambda $
the expansion condition (Definition 3.4) enables us to encode points of
![]() $\Lambda $
by sequences in the finite index set
$\Lambda $
by sequences in the finite index set
![]() $\mathcal {I}$
. Roughly speaking, for each
$\mathcal {I}$
. Roughly speaking, for each
![]() $x\in \Lambda $
, we keep zooming in toward x using the ‘microscope’, namely, the expanding maps
$x\in \Lambda $
, we keep zooming in toward x using the ‘microscope’, namely, the expanding maps
![]() $\rho (s_{\alpha (k)}^{-1})$
. This is the heuristic Sullivan himself used in his talk according to F. Bonahon. (We thank Bonahon for telling us his personal anecdote.)
$\rho (s_{\alpha (k)}^{-1})$
. This is the heuristic Sullivan himself used in his talk according to F. Bonahon. (We thank Bonahon for telling us his personal anecdote.)
Definition 3.10 (Codes)
Suppose an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
. Let
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
. Let
![]() $x\in \Lambda $
and fix a real number
$x\in \Lambda $
and fix a real number
![]() $\eta $
such that
$\eta $
such that
![]() $0<\eta \le \delta $
. Given a sequence
$0<\eta \le \delta $
. Given a sequence
![]() $\alpha :\mathbb {N}_0\to \mathcal {I},\;k\mapsto \alpha (k)$
, define a sequence
$\alpha :\mathbb {N}_0\to \mathcal {I},\;k\mapsto \alpha (k)$
, define a sequence
![]() $p:\mathbb {N}_0\to \Lambda ,\;k\mapsto p_k$
inductively by
$p:\mathbb {N}_0\to \Lambda ,\;k\mapsto p_k$
inductively by
 $$ \begin{align*} p_0&=x,\\ p_{k+1}&=\rho(s_{\alpha(k)}^{-1})(p_k). \end{align*} $$
$$ \begin{align*} p_0&=x,\\ p_{k+1}&=\rho(s_{\alpha(k)}^{-1})(p_k). \end{align*} $$
The sequence
![]() $\alpha $
(or the pair
$\alpha $
(or the pair
![]() $(\alpha ,p)$
of sequences) is called a
$(\alpha ,p)$
of sequences) is called a
![]() $(\mathcal {D},\eta )$
-code for x if
$(\mathcal {D},\eta )$
-code for x if
for every
![]() $k\in \mathbb {N}$
. (When
$k\in \mathbb {N}$
. (When
![]() $\mathcal {D}$
is understood, we simply say an
$\mathcal {D}$
is understood, we simply say an
![]() $\eta $
-code in order to emphasize the use of
$\eta $
-code in order to emphasize the use of
![]() $\eta $
-balls). A
$\eta $
-balls). A
![]() $(\mathcal {D},\eta )$
-code
$(\mathcal {D},\eta )$
-code
![]() $\alpha $
for x is said to be special if
$\alpha $
for x is said to be special if
![]() $\alpha (0)$
satisfies
$\alpha (0)$
satisfies
![]() $B_{\eta }(x)\subset U_{\alpha (0)}$
. We denote by
$B_{\eta }(x)\subset U_{\alpha (0)}$
. We denote by
![]() $\mathrm {Code}_x(\mathcal {D},\eta )$
the set of all
$\mathrm {Code}_x(\mathcal {D},\eta )$
the set of all
![]() $(\mathcal {D},\eta )$
-codes for
$(\mathcal {D},\eta )$
-codes for
![]() $x\in \Lambda $
.
$x\in \Lambda $
.
Every
![]() $\eta $
-ball centered at a point on
$\eta $
-ball centered at a point on
![]() $\Lambda $
is contained in some member of
$\Lambda $
is contained in some member of
![]() $\mathcal {U}$
since
$\mathcal {U}$
since
![]() $\eta \le \delta \le \delta _{\mathcal {U}}$
. This enables us to construct codes. A code gives rise to a family of
$\eta \le \delta \le \delta _{\mathcal {U}}$
. This enables us to construct codes. A code gives rise to a family of
![]() $\eta $
-balls centered at points in
$\eta $
-balls centered at points in
![]() $\Lambda $
each of which is a
$\Lambda $
each of which is a
![]() $\lambda $
-expanding domain for the action on M of some element of
$\lambda $
-expanding domain for the action on M of some element of
![]() $\Gamma $
.
$\Gamma $
.
Remark 3.11.
-
(a) That we do not require
 $\alpha (0)$
to satisfy
$\alpha (0)$
to satisfy
 $B_{\eta }(x)\subset U_{\alpha (0)}$
in general is Sullivan’s trick, which will be useful to prove equivariance of the conjugacy
$B_{\eta }(x)\subset U_{\alpha (0)}$
in general is Sullivan’s trick, which will be useful to prove equivariance of the conjugacy
 $\phi $
in Section 4.5.
$\phi $
in Section 4.5. -
(b) The requirement
 $B_{\eta }(p_k)\subset U_{\alpha (k)}$
implies
$B_{\eta }(p_k)\subset U_{\alpha (k)}$
implies
 $U_{\alpha (k)}\neq \emptyset $
for
$U_{\alpha (k)}\neq \emptyset $
for
 $k\in \mathbb {N}$
. Thus, only for the initial value
$k\in \mathbb {N}$
. Thus, only for the initial value
 $\alpha (0)$
of codes
$\alpha (0)$
of codes
 $\alpha $
can we possibly have
$\alpha $
can we possibly have
 $U_{\alpha (0)}=\emptyset $
.
$U_{\alpha (0)}=\emptyset $
. -
(c) Since
 $\delta \le \delta _{\mathcal {U}}$
, we have
$\delta \le \delta _{\mathcal {U}}$
, we have
 $\mathrm {Code}_x(\mathcal {D},\eta )\neq \emptyset $
for all
$\mathrm {Code}_x(\mathcal {D},\eta )\neq \emptyset $
for all
 $x\in \Lambda $
and
$x\in \Lambda $
and
 $0<\eta \le \delta $
, and special codes always exist for any point. Moreover, if
$0<\eta \le \delta $
, and special codes always exist for any point. Moreover, if
 $\eta '\le \eta \le \delta $
, then
$\eta '\le \eta \le \delta $
, then
 $\mathrm {Code}_x(\mathcal {D},\eta )\subset \mathrm {Code}_x(\mathcal {D},\eta ')$
. Indeed, if
$\mathrm {Code}_x(\mathcal {D},\eta )\subset \mathrm {Code}_x(\mathcal {D},\eta ')$
. Indeed, if
 $(\alpha ,p)$
is an
$(\alpha ,p)$
is an
 $\eta $
-code for x, then
$\eta $
-code for x, then
 $B_{\eta '}(p_k)\subset B_{\eta }(p_k)\subset U_{\alpha (k)}$
for all
$B_{\eta '}(p_k)\subset B_{\eta }(p_k)\subset U_{\alpha (k)}$
for all
 $k\in \mathbb {N}$
, which implies that
$k\in \mathbb {N}$
, which implies that
 $(\alpha ,p)$
is an
$(\alpha ,p)$
is an
 $\eta '$
-code for x as well.
$\eta '$
-code for x as well. -
(d) If
 $\mathcal {D}_0$
and
$\mathcal {D}_0$
and
 $\mathcal {D}_1$
are expansion data of
$\mathcal {D}_1$
are expansion data of
 $\rho $
and
$\rho $
and
 $\mathcal {D}_0\prec \mathcal {D}_1$
, then for any
$\mathcal {D}_0\prec \mathcal {D}_1$
, then for any
 $\eta \le \delta _1\le \delta _0$
, a
$\eta \le \delta _1\le \delta _0$
, a
 $(\mathcal {D}_0,\eta )$
-code
$(\mathcal {D}_0,\eta )$
-code
 $\alpha :\mathbb {N}_0\to \mathcal {I}_0\subset \mathcal {I}_1$
for x may be regarded as a
$\alpha :\mathbb {N}_0\to \mathcal {I}_0\subset \mathcal {I}_1$
for x may be regarded as a
 $(\mathcal {D}_1,\eta )$
-code. Slightly abusing the notation, we write this relation as
$(\mathcal {D}_1,\eta )$
-code. Slightly abusing the notation, we write this relation as
 $\mathrm {Code}_x(\mathcal {D}_0,\eta )\subset \mathrm {Code}_x(\mathcal {D}_1,\eta )$
.
$\mathrm {Code}_x(\mathcal {D}_0,\eta )\subset \mathrm {Code}_x(\mathcal {D}_1,\eta )$
.
Definition 3.12 (Rays)
Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with the datum
$\Lambda $
with the datum
![]() $\mathcal {D}$
. Given a
$\mathcal {D}$
. Given a
![]() $(\mathcal {D},\eta )$
-code
$(\mathcal {D},\eta )$
-code
![]() $\alpha $
for
$\alpha $
for
![]() $x\in \Lambda $
, the
$x\in \Lambda $
, the
![]() $(\mathcal {D},\eta )$
-ray (or simply
$(\mathcal {D},\eta )$
-ray (or simply
![]() $\eta $
-ray) associated to
$\eta $
-ray) associated to
![]() $\alpha $
is a sequence
$\alpha $
is a sequence
![]() $c^{\alpha }:\mathbb {N}_0\to \Gamma $
defined by
$c^{\alpha }:\mathbb {N}_0\to \Gamma $
defined by
We set
![]() $\mathrm {Ray}_x(\mathcal {D},\eta ):=\{c^{\alpha }\mid \alpha \in \mathrm {Code}_x(\mathcal {D},\eta )\}$
and interpret c as a map
$\mathrm {Ray}_x(\mathcal {D},\eta ):=\{c^{\alpha }\mid \alpha \in \mathrm {Code}_x(\mathcal {D},\eta )\}$
and interpret c as a map
Remark 3.13.
-
(a) The initial point
 $c^{\alpha }_0= s_{\alpha (0)}$
of
$c^{\alpha }_0= s_{\alpha (0)}$
of
 $c^{\alpha }$
is an element of
$c^{\alpha }$
is an element of
 $\varSigma $
.
$\varSigma $
. -
(b) From the definition of codes, it is easy to check that
 $\rho (c^{\alpha }_k)(p_{k+1})=p_0=x$
for every
$\rho (c^{\alpha }_k)(p_{k+1})=p_0=x$
for every
 $k\in \mathbb {N}_0$
.
$k\in \mathbb {N}_0$
. -
(c) Every ray
 $c^{\alpha }$
defines an edge-path in the Cayley graph
$c^{\alpha }$
defines an edge-path in the Cayley graph
 $(\Gamma ,d_{\varSigma })$
of
$(\Gamma ,d_{\varSigma })$
of
 $\Gamma $
(with respect to the generating set
$\Gamma $
(with respect to the generating set
 $\varSigma $
). Note that each word
$\varSigma $
). Note that each word
 $s_{\alpha (0)}^{-1}c^{\alpha }_k=s_{\alpha (1)}\cdots s_{\alpha (k)} (k>1)$
is reduced, since an appearance of
$s_{\alpha (0)}^{-1}c^{\alpha }_k=s_{\alpha (1)}\cdots s_{\alpha (k)} (k>1)$
is reduced, since an appearance of
 $s^{-1}s$
for
$s^{-1}s$
for
 $s\in \varSigma $
would imply that the composite map
$s\in \varSigma $
would imply that the composite map
 $\rho (s^{-1})\rho (s)$
, which is the identity, is
$\rho (s^{-1})\rho (s)$
, which is the identity, is
 $\lambda ^2$
-expanding on some nonempty open subset of M.
$\lambda ^2$
-expanding on some nonempty open subset of M. -
(d) If
 $(\varSigma _0,\delta _0)=\mathcal {D}_0\prec \mathcal {D}_1=(\varSigma _1,\delta _1)$
are expansion data of
$(\varSigma _0,\delta _0)=\mathcal {D}_0\prec \mathcal {D}_1=(\varSigma _1,\delta _1)$
are expansion data of
 $\rho $
and
$\rho $
and
 $\eta \le \delta _1\le \delta _0$
, then we have
$\eta \le \delta _1\le \delta _0$
, then we have
 $\mathrm {Ray}_x(\mathcal {D}_0,\eta )\subset \mathrm {Ray}_x(\mathcal {D}_1,\eta )$
as in Remark 3.11(d).
$\mathrm {Ray}_x(\mathcal {D}_0,\eta )\subset \mathrm {Ray}_x(\mathcal {D}_1,\eta )$
as in Remark 3.11(d).
Now, we will see that, for every
![]() $x\in \Lambda $
, each
$x\in \Lambda $
, each
![]() $\eta $
-code for x gives rise to a nested sequence of neighborhoods of x whose diameters tend to
$\eta $
-code for x gives rise to a nested sequence of neighborhoods of x whose diameters tend to
![]() $0$
exponentially fast.
$0$
exponentially fast.
Lemma 3.14. Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
, and let
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
, and let
![]() $0<\eta \le \delta $
. If
$0<\eta \le \delta $
. If
![]() $(\alpha ,p)$
is a
$(\alpha ,p)$
is a
![]() $(\mathcal {D},\eta )$
-code for
$(\mathcal {D},\eta )$
-code for
![]() $x\in \Lambda $
, then the sequence of neighborhoods of x
$x\in \Lambda $
, then the sequence of neighborhoods of x
is nested and exponentially shrinking. More precisely, we have
-
(i)
 $\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]\subset \rho (c^{\alpha }_{k-1})[B_{\eta }(p_k)]$
for
$\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]\subset \rho (c^{\alpha }_{k-1})[B_{\eta }(p_k)]$
for
 $k\in \mathbb {N}$
, and
$k\in \mathbb {N}$
, and -
(ii)
 $\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})] \subset B_{L\eta /\lambda ^{k}}(x)$
for all
$\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})] \subset B_{L\eta /\lambda ^{k}}(x)$
for all
 $k\in \mathbb {N}_0$
.
$k\in \mathbb {N}_0$
.
Consequently, we have the equality
 $$\begin{align*}\{x\}=\bigcap_{k=0}^{\infty}\rho(c^{\alpha}_k)[B_{\eta}(p_{k+1})]. \end{align*}$$
$$\begin{align*}\{x\}=\bigcap_{k=0}^{\infty}\rho(c^{\alpha}_k)[B_{\eta}(p_{k+1})]. \end{align*}$$
The map
![]() $\rho (c^{\alpha }_k)^{-1}$
is
$\rho (c^{\alpha }_k)^{-1}$
is
![]() $\lambda ^k/L$
-expanding on the neighborhood
$\lambda ^k/L$
-expanding on the neighborhood
![]() $\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]$
of x for all
$\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]$
of x for all
![]() $k\in \mathbb {N}_0$
, and the map
$k\in \mathbb {N}_0$
, and the map
is
![]() $\lambda ^{k-j}$
-expanding on
$\lambda ^{k-j}$
-expanding on
![]() $\rho (c^{\alpha }_j)^{-1}\big [\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]\big ]$
for all
$\rho (c^{\alpha }_j)^{-1}\big [\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]\big ]$
for all
![]() $0\le j< k$
.
$0\le j< k$
.
Proof. Suppose
![]() $(\alpha ,p)$
is an
$(\alpha ,p)$
is an
![]() $\eta $
-code for
$\eta $
-code for
![]() $x\in \Lambda $
, and let
$x\in \Lambda $
, and let
![]() $k\in \mathbb {N}$
. Since
$k\in \mathbb {N}$
. Since
![]() $B_{\eta }(p_k)\subset U_{\alpha (k)}$
and the homeomorphism
$B_{\eta }(p_k)\subset U_{\alpha (k)}$
and the homeomorphism
![]() $\rho (s_{\alpha (k)}^{-1})$
is
$\rho (s_{\alpha (k)}^{-1})$
is
![]() $(\lambda ,U_{\alpha (k)};\delta )$
-expanding with
$(\lambda ,U_{\alpha (k)};\delta )$
-expanding with
![]() $\rho (s_{\alpha (k)}^{-1})(p_k)=p_{k+1}$
, we have by definition
$\rho (s_{\alpha (k)}^{-1})(p_k)=p_{k+1}$
, we have by definition
On the other hand, the inverse map
![]() $\rho (s_{\alpha (k)})$
is
$\rho (s_{\alpha (k)})$
is
![]() $(\lambda ^{-1},\rho (s_{\alpha (k)}^{-1})[U_{\alpha (k)}])$
-contracting as we saw in Remark 3.6(d). Since
$(\lambda ^{-1},\rho (s_{\alpha (k)}^{-1})[U_{\alpha (k)}])$
-contracting as we saw in Remark 3.6(d). Since
![]() $B_{\eta }(p_{k+1})\subset \rho (s_{\alpha (k)}^{-1})[U_{\alpha (k)}]$
, we obtain
$B_{\eta }(p_{k+1})\subset \rho (s_{\alpha (k)}^{-1})[U_{\alpha (k)}]$
, we obtain
See Figure 2. By a similar reasoning, we inductively obtain
 $$ \begin{align*} \rho(s_{\alpha(k-1)}s_{\alpha(k)})[B_{\eta}(p_{k+1})] &\subset B_{\eta/\lambda^2}(p_{k-1}),\\ &\;\;\vdots \\ \rho(s_{\alpha(1)}\cdots s_{\alpha(k-1)}s_{\alpha(k)})[B_{\eta}(p_{k+1})] &\subset B_{\eta/\lambda^{k}}(p_1). \end{align*} $$
$$ \begin{align*} \rho(s_{\alpha(k-1)}s_{\alpha(k)})[B_{\eta}(p_{k+1})] &\subset B_{\eta/\lambda^2}(p_{k-1}),\\ &\;\;\vdots \\ \rho(s_{\alpha(1)}\cdots s_{\alpha(k-1)}s_{\alpha(k)})[B_{\eta}(p_{k+1})] &\subset B_{\eta/\lambda^{k}}(p_1). \end{align*} $$
Lastly, the map
![]() $\rho (s_{\alpha (0)})$
is L-Lipschitz on
$\rho (s_{\alpha (0)})$
is L-Lipschitz on
![]() $B_{\eta /\lambda ^{k}}(p_1)\subset N_{\delta }(\Lambda )$
by Definition 3.4(i). Thus, we see that
$B_{\eta /\lambda ^{k}}(p_1)\subset N_{\delta }(\Lambda )$
by Definition 3.4(i). Thus, we see that
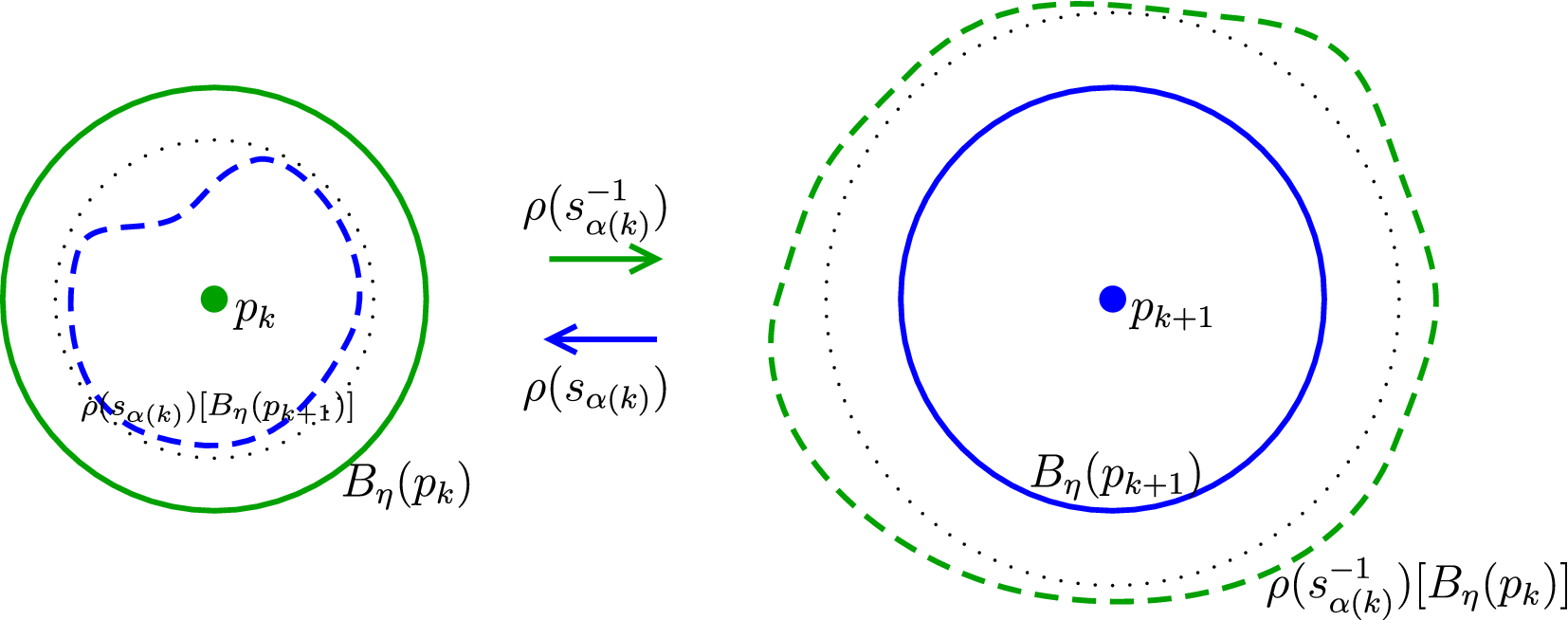
Figure 2 Actions of
![]() $\rho (s_{\alpha (k)}^{-1})$
and
$\rho (s_{\alpha (k)}^{-1})$
and
![]() $\rho (s_{\alpha (k)})$
for
$\rho (s_{\alpha (k)})$
for
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
Since
![]() $\rho (c^{\alpha }_k)(p_{k+1})=p_0=x$
, the inclusion (3.17) can be written as
$\rho (c^{\alpha }_k)(p_{k+1})=p_0=x$
, the inclusion (3.17) can be written as
for all
![]() $k\in \mathbb {N}_0$
. Moreover, from equation (3.16) we have
$k\in \mathbb {N}_0$
. Moreover, from equation (3.16) we have
 $$ \begin{align} \begin{aligned} \rho(c^{\alpha}_k)[B_{\eta}(p_{k+1})] &=\rho(s_{\alpha(0)}\cdots s_{\alpha(k-1)} s_{\alpha(k)})[B_{\eta}(p_{k+1})] \\ &\subset \rho(s_{\alpha(0)}\cdots s_{\alpha(k-1)})[B_{\eta}(p_k)]\\ &= \rho(c^{\alpha}_{k-1})[B_{\eta}(p_k)] \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \rho(c^{\alpha}_k)[B_{\eta}(p_{k+1})] &=\rho(s_{\alpha(0)}\cdots s_{\alpha(k-1)} s_{\alpha(k)})[B_{\eta}(p_{k+1})] \\ &\subset \rho(s_{\alpha(0)}\cdots s_{\alpha(k-1)})[B_{\eta}(p_k)]\\ &= \rho(c^{\alpha}_{k-1})[B_{\eta}(p_k)] \end{aligned} \end{align} $$
for all
![]() $k\in \mathbb {N}$
. From these follows the rest of the lemma.
$k\in \mathbb {N}$
. From these follows the rest of the lemma.
A number of corollaries will follow.
We say an action
![]() $\rho :\Gamma \to \mathrm {Homeo}(M)$
with an invariant subset
$\rho :\Gamma \to \mathrm {Homeo}(M)$
with an invariant subset
![]() $\Lambda $
has an expansivity constant
$\Lambda $
has an expansivity constant
![]() $c>0$
if for every distinct pair of points
$c>0$
if for every distinct pair of points
![]() $x,y\in \Lambda $
there exists an element
$x,y\in \Lambda $
there exists an element
![]() $g\in \Gamma $
such that
$g\in \Gamma $
such that
![]() $d(\rho (g)(x),\rho (g)(y))\ge c$
. Compare [Reference Coornaert and Papadopoulos11, Proposition 2.2.4].
$d(\rho (g)(x),\rho (g)(y))\ge c$
. Compare [Reference Coornaert and Papadopoulos11, Proposition 2.2.4].
Corollary 3.19. If an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\delta )$
, then
$\mathcal {D}=(\delta )$
, then
![]() $\delta $
is an expansivity constant of this action.
$\delta $
is an expansivity constant of this action.
Proof. Let
![]() $x,y\in \Lambda $
be distinct, and consider a
$x,y\in \Lambda $
be distinct, and consider a
![]() $\delta $
-code
$\delta $
-code
![]() $(\alpha ,p)$
for x. By Lemma 3.14, the sequence of neighborhoods of x
$(\alpha ,p)$
for x. By Lemma 3.14, the sequence of neighborhoods of x
is nested and exponentially shrinking. Thus, there exists an
![]() $n\in \mathbb {N}_0$
such that
$n\in \mathbb {N}_0$
such that
Therefore,
![]() $d(\rho (c^{\alpha }_n)^{-1}(x),\rho (c^{\alpha }_n)^{-1}(y))\ge \delta $
as desired.
$d(\rho (c^{\alpha }_n)^{-1}(x),\rho (c^{\alpha }_n)^{-1}(y))\ge \delta $
as desired.
The following corollary will be crucial for Definition 6.1, which in turn plays an essential role when we discuss actions of hyperbolic groups in Section 6. The corollary is also the reason why we need the assumption that no point of
![]() $\Lambda $
is isolated in M.
$\Lambda $
is isolated in M.
Corollary 3.20. Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\varSigma ,\delta ,L,\lambda )$
. Let
$\mathcal {D}=(\varSigma ,\delta ,L,\lambda )$
. Let
![]() $\eta \in (0,\delta ]$
and
$\eta \in (0,\delta ]$
and
![]() $\alpha $
be an
$\alpha $
be an
![]() $\eta $
-code for
$\eta $
-code for
![]() $x \in \Lambda $
. Then the ray
$x \in \Lambda $
. Then the ray
![]() $c^{\alpha }\in \mathrm {Ray}_x(\mathcal {D},\eta )$
is a
$c^{\alpha }\in \mathrm {Ray}_x(\mathcal {D},\eta )$
is a
![]() $(\frac {\log L}{\log \lambda },0)$
-quasi-geodesic ray in
$(\frac {\log L}{\log \lambda },0)$
-quasi-geodesic ray in
![]() $(\Gamma ,d_{\varSigma })$
.
$(\Gamma ,d_{\varSigma })$
.
Proof. Let
![]() $(\alpha ,p)$
be an
$(\alpha ,p)$
be an
![]() $\eta $
-code for
$\eta $
-code for
![]() $x\in \Lambda $
. Since no point of
$x\in \Lambda $
. Since no point of
![]() $\Lambda $
is isolated in M, for each
$\Lambda $
is isolated in M, for each
![]() $k\in \mathbb {N}_0$
we can choose a point
$k\in \mathbb {N}_0$
we can choose a point
![]() $y_k$
such that
$y_k$
such that
Let
![]() $k,j\in \mathbb {N}_0$
be such that
$k,j\in \mathbb {N}_0$
be such that
![]() $0\le j<k$
, and set
$0\le j<k$
, and set
![]() $r_{kj}:=(c^{\alpha }_k)^{-1}c^{\alpha }_j$
. By (the last statement of) Lemma 3.14, the map
$r_{kj}:=(c^{\alpha }_k)^{-1}c^{\alpha }_j$
. By (the last statement of) Lemma 3.14, the map
![]() $\rho (r_{kj})$
is
$\rho (r_{kj})$
is
![]() $\lambda ^{k-j}$
-expanding on
$\lambda ^{k-j}$
-expanding on
![]() $\rho (c^{\alpha }_j)^{-1}\big [\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]\big ]\supset \{\rho (c^{\alpha }_j)^{-1}(y_k),\rho (c^{\alpha }_j)^{-1}(x)\}$
, hence
$\rho (c^{\alpha }_j)^{-1}\big [\rho (c^{\alpha }_k)[B_{\eta }(p_{k+1})]\big ]\supset \{\rho (c^{\alpha }_j)^{-1}(y_k),\rho (c^{\alpha }_j)^{-1}(x)\}$
, hence
where we set
![]() $y_{kj}:=\rho (c^{\alpha }_j)^{-1}(y_k)$
and
$y_{kj}:=\rho (c^{\alpha }_j)^{-1}(y_k)$
and
![]() $x_{j}:=\rho (c^{\alpha }_j)^{-1}(x)$
. On the other hand, we have
$x_{j}:=\rho (c^{\alpha }_j)^{-1}(x)$
. On the other hand, we have
from equation (3.5), since
![]() $x_{j}\in \Lambda $
while
$x_{j}\in \Lambda $
while
![]() $y_{kj}\in N_{\delta /L^{k-j-1}}(\Lambda )$
and
$y_{kj}\in N_{\delta /L^{k-j-1}}(\Lambda )$
and
![]() $|r_{kj}|_{\varSigma }\le k-j$
. From these two inequalities, we obtain
$|r_{kj}|_{\varSigma }\le k-j$
. From these two inequalities, we obtain
Therefore, the
![]() $\eta $
-ray
$\eta $
-ray
![]() $c^{\alpha }$
is a
$c^{\alpha }$
is a
![]() $(\frac {\log L}{\log \lambda },0)$
-quasi-geodesic ray.
$(\frac {\log L}{\log \lambda },0)$
-quasi-geodesic ray.
Another consequence of the encoding concerns the dynamics of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
. The action of
$\Lambda $
. The action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
need not be minimal in general even if
$\Lambda $
need not be minimal in general even if
![]() $\Gamma $
is a nonelementary hyperbolic group (see Example 7.4). Nevertheless, the action of
$\Gamma $
is a nonelementary hyperbolic group (see Example 7.4). Nevertheless, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
has no wandering points:
$\Lambda $
has no wandering points:
Theorem 3.21. Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\delta )$
. For
$\mathcal {D}=(\delta )$
. For
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $\eta \in (0,\delta ]$
, consider a ray
$\eta \in (0,\delta ]$
, consider a ray
![]() $c^{\alpha }\in \mathrm {Ray}_x(\mathcal {D},\eta )$
associated to an
$c^{\alpha }\in \mathrm {Ray}_x(\mathcal {D},\eta )$
associated to an
![]() $\eta $
-code
$\eta $
-code
![]() $(\alpha ,p)$
for x. Then
$(\alpha ,p)$
for x. Then
-
(1) there exist a subsequence
 $(g_j)$
of
$(g_j)$
of
 $(c^{\alpha }_k)$
and a point
$(c^{\alpha }_k)$
and a point
 $y\in \Lambda $
such that
$y\in \Lambda $
such that
 $(\rho (g_j))$
converges to x uniformly on
$(\rho (g_j))$
converges to x uniformly on
 $B_{\eta /2}(y)$
;
$B_{\eta /2}(y)$
; -
(2) there exists an infinite sequence
 $(h_j)$
in
$(h_j)$
in
 $\Gamma $
such that
$\Gamma $
such that  $$\begin{align*}\lim_{j\to \infty} \rho(h_j)(x)=x. \end{align*}$$
$$\begin{align*}\lim_{j\to \infty} \rho(h_j)(x)=x. \end{align*}$$
Proof. (1) By the compactness of
![]() $\Lambda $
, the sequence
$\Lambda $
, the sequence
![]() $p=(p_k)$
contains a subsequence
$p=(p_k)$
contains a subsequence
![]() $(p_{k_j+1})$
converging to some point
$(p_{k_j+1})$
converging to some point
![]() $y\in \Lambda $
. The point y is then covered by infinitely many balls
$y\in \Lambda $
. The point y is then covered by infinitely many balls
![]() $B_{\eta /2}(p_{k_j+1})$
,
$B_{\eta /2}(p_{k_j+1})$
,
![]() $j\in \mathbb {N}$
. By Lemma 3.14, the corresponding elements
$j\in \mathbb {N}$
. By Lemma 3.14, the corresponding elements
![]() $g_j:= c^{\alpha }_{k_j}\in \Gamma $
will send
$g_j:= c^{\alpha }_{k_j}\in \Gamma $
will send
![]() $B_{\eta /2}(y)\subset B_{\eta }(p_{k_j+1})$
to a subset
$B_{\eta /2}(y)\subset B_{\eta }(p_{k_j+1})$
to a subset
![]() $\rho (g_j)[B_{\eta /2}(y)]$
of diameter at most
$\rho (g_j)[B_{\eta /2}(y)]$
of diameter at most
![]() $L\eta /\lambda ^{k_j}$
containing x. From this, we conclude that the sequence
$L\eta /\lambda ^{k_j}$
containing x. From this, we conclude that the sequence
![]() $(\rho (g_j))$
converges to x uniformly on
$(\rho (g_j))$
converges to x uniformly on
![]() $B_{\eta /2}(y)$
.
$B_{\eta /2}(y)$
.
(2) On the other hand, since, in particular,
![]() $p_{k_1+1}\in B_{\eta /2}(y)$
, we obtain
$p_{k_1+1}\in B_{\eta /2}(y)$
, we obtain
Since
![]() $\rho (c^{\alpha }_{k_1})^{-1}(x)=p_{k_1+1}$
, it follows that for
$\rho (c^{\alpha }_{k_1})^{-1}(x)=p_{k_1+1}$
, it follows that for
![]() $h_j:= c^{\alpha }_{k_j} (c^{\alpha }_{k_1})^{-1}$
we have
$h_j:= c^{\alpha }_{k_j} (c^{\alpha }_{k_1})^{-1}$
we have
Remark 3.22. The idea of Markov coding of limit points of actions of finitely generated groups
![]() $\Gamma $
by sequences in
$\Gamma $
by sequences in
![]() $\Gamma $
is rather standard in symbolic dynamics and goes back to Nielsen, Hedlund and Morse; we refer the reader to the paper by Series [Reference Series33] for references and historical discussion. In the setting of hyperbolic groups this was introduced in Gromov’s paper [Reference Gromov18, §.8] and discussed in more detail in the book by Coornaert and Papadopoulos [Reference Coornaert and Papadopoulos11]. Section 8.5.Y of Gromov’s paper discusses a relation to Sullivan’s stability theorem.
$\Gamma $
is rather standard in symbolic dynamics and goes back to Nielsen, Hedlund and Morse; we refer the reader to the paper by Series [Reference Series33] for references and historical discussion. In the setting of hyperbolic groups this was introduced in Gromov’s paper [Reference Gromov18, §.8] and discussed in more detail in the book by Coornaert and Papadopoulos [Reference Coornaert and Papadopoulos11]. Section 8.5.Y of Gromov’s paper discusses a relation to Sullivan’s stability theorem.
3.4 The meandering hyperbolicity condition
We continue the discussion from the previous section. In order to define the meandering hyperbolicity condition, we need to introduce an equivalence relation
![]() $\sim ^N_{(\mathcal {D},\eta )}$
on the set
$\sim ^N_{(\mathcal {D},\eta )}$
on the set
![]() $\mathrm {Ray}_x(\mathcal {D},\eta )$
of rays in
$\mathrm {Ray}_x(\mathcal {D},\eta )$
of rays in
![]() $\Gamma $
associated to
$\Gamma $
associated to
![]() $(\mathcal {D},\eta )$
-codes for
$(\mathcal {D},\eta )$
-codes for
![]() $x\in \Lambda $
; recall Definitions 3.10 and 3.12.
$x\in \Lambda $
; recall Definitions 3.10 and 3.12.
Definition 3.23 (
 $(\mathcal {D},\eta ;N)$
-equivalence)
$(\mathcal {D},\eta ;N)$
-equivalence)
Suppose
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\varSigma ,\delta )$
, and let
$\mathcal {D}=(\varSigma ,\delta )$
, and let
![]() $0<\eta \le \delta $
.
$0<\eta \le \delta $
.
-
(a) For each integer
 $N\ge 0$
, we define the relation
$N\ge 0$
, we define the relation
 $\approx ^N_{(\mathcal {D},\eta )}$
on
$\approx ^N_{(\mathcal {D},\eta )}$
on
 $\mathrm {Ray}_x(\mathcal {D},\eta )$
by declaring that
$\mathrm {Ray}_x(\mathcal {D},\eta )$
by declaring that
 $c^{\alpha } \approx ^N_{(\mathcal {D},\eta )} c^{\beta }$
if there exist infinite subsets
$c^{\alpha } \approx ^N_{(\mathcal {D},\eta )} c^{\beta }$
if there exist infinite subsets
 $P,\,Q\subset \mathbb {N}_0$
such that the subsets of
$P,\,Q\subset \mathbb {N}_0$
such that the subsets of $$\begin{align*}c^{\alpha}(P)=\{c^{\alpha}_k \mid k\in P\}\quad\mathrm{and}\quad c^{\beta}(Q)=\{c^{\beta}_j \mid j\in Q\} \end{align*}$$
$$\begin{align*}c^{\alpha}(P)=\{c^{\alpha}_k \mid k\in P\}\quad\mathrm{and}\quad c^{\beta}(Q)=\{c^{\beta}_j \mid j\in Q\} \end{align*}$$
 $(\Gamma ,d_{\varSigma })$
are within Hausdorff distance N from each other. The
$(\Gamma ,d_{\varSigma })$
are within Hausdorff distance N from each other. The
 $(\mathcal {D},\eta ;N)$
-equivalence, denoted
$(\mathcal {D},\eta ;N)$
-equivalence, denoted
 $\sim ^N_{(\mathcal {D},\eta )}$
, is the equivalence relation on the set
$\sim ^N_{(\mathcal {D},\eta )}$
, is the equivalence relation on the set
 $\mathrm {Ray}_x(\mathcal {D},\eta )$
generated by the relation
$\mathrm {Ray}_x(\mathcal {D},\eta )$
generated by the relation
 $\approx ^N_{(\mathcal {D},\eta )}$
. In other words, we write
$\approx ^N_{(\mathcal {D},\eta )}$
. In other words, we write
 $c^{\alpha }\sim ^N_{(\mathcal {D},\eta )} c^{\beta }$
and say
$c^{\alpha }\sim ^N_{(\mathcal {D},\eta )} c^{\beta }$
and say
 $c^{\alpha }$
and
$c^{\alpha }$
and
 $c^{\beta }$
are
$c^{\beta }$
are
 $(\mathcal {D},\eta ;N)$
-equivalent if there is a finite chain of ‘interpolating’ rays
$(\mathcal {D},\eta ;N)$
-equivalent if there is a finite chain of ‘interpolating’ rays
 $c^{\alpha }=c^{\gamma _1}, c^{\gamma _2},\ldots , c^{\gamma _n}=c^{\beta }$
in
$c^{\alpha }=c^{\gamma _1}, c^{\gamma _2},\ldots , c^{\gamma _n}=c^{\beta }$
in
 $\mathrm {Ray}_x(\mathcal {D},\eta )$
such that
$\mathrm {Ray}_x(\mathcal {D},\eta )$
such that  $$\begin{align*}c^{\gamma_1} \approx^N_{(\mathcal{D},\eta)} c^{\gamma_2} \approx^N_{(\mathcal{D},\eta)} \cdots \approx^N_{(\mathcal{D},\eta)} c^{\gamma_n}. \end{align*}$$
$$\begin{align*}c^{\gamma_1} \approx^N_{(\mathcal{D},\eta)} c^{\gamma_2} \approx^N_{(\mathcal{D},\eta)} \cdots \approx^N_{(\mathcal{D},\eta)} c^{\gamma_n}. \end{align*}$$
-
(b) The
 $(\mathcal {D},\eta )$
-rays
$(\mathcal {D},\eta )$
-rays
 $c^{\alpha }$
and
$c^{\alpha }$
and
 $c^{\beta }$
are said to
$c^{\beta }$
are said to
 $(\mathcal {D},\eta ;N)$
-fellow-travel if their images
$(\mathcal {D},\eta ;N)$
-fellow-travel if their images
 $c^{\alpha }(\mathbb {N}_0)$
and
$c^{\alpha }(\mathbb {N}_0)$
and
 $c^{\beta }(\mathbb {N}_0)$
are within Hausdorff distance N from each other.
$c^{\beta }(\mathbb {N}_0)$
are within Hausdorff distance N from each other.
Remark 3.24.
-
(a) Observe that
 $(\mathcal {D},\eta ;N)$
-fellow-traveling rays are
$(\mathcal {D},\eta ;N)$
-fellow-traveling rays are
 $(\mathcal {D},\eta ;N)$
-equivalent.
$(\mathcal {D},\eta ;N)$
-equivalent. -
(b) The notion of
 $(\mathcal {D},\eta ;N)$
-equivalence is much more complex than that of
$(\mathcal {D},\eta ;N)$
-equivalence is much more complex than that of
 $(\mathcal {D},\eta ;N)$
-fellow-traveling for a reason: While fellow-traveling is a natural condition in the context of hyperbolic groups where quasi-geodesics with common end points uniformly fellow-travel, our notion of equivalence is defined this way in order to incorporate nonhyperbolic groups, such as higher rank uniform lattices, into the theory of hyperbolic group actions. In all examples that we have, two rays are
$(\mathcal {D},\eta ;N)$
-fellow-traveling for a reason: While fellow-traveling is a natural condition in the context of hyperbolic groups where quasi-geodesics with common end points uniformly fellow-travel, our notion of equivalence is defined this way in order to incorporate nonhyperbolic groups, such as higher rank uniform lattices, into the theory of hyperbolic group actions. In all examples that we have, two rays are
 $(\mathcal {D},\eta ;N)$
-equivalent if and only if they admit an interpolation by at most one extra ray. However, in general, we see no reason for interpolation via one ray to define an equivalence relation on coding rays. A picture describing the behavior of an interpolating ray can be found in Figure 4 in Section 5.4: The red interpolating ray ‘meanders’ between the two black rays. This explains the terminology meandering hyperbolicity.
$(\mathcal {D},\eta ;N)$
-equivalent if and only if they admit an interpolation by at most one extra ray. However, in general, we see no reason for interpolation via one ray to define an equivalence relation on coding rays. A picture describing the behavior of an interpolating ray can be found in Figure 4 in Section 5.4: The red interpolating ray ‘meanders’ between the two black rays. This explains the terminology meandering hyperbolicity. -
(c) If
 $(\varSigma _0,\delta _0)=\mathcal {D}_0\prec \mathcal {D}=(\varSigma ,\delta )$
and
$(\varSigma _0,\delta _0)=\mathcal {D}_0\prec \mathcal {D}=(\varSigma ,\delta )$
and
 $\eta \le \delta <\delta _0$
, then we have the inclusion
$\eta \le \delta <\delta _0$
, then we have the inclusion
 $\mathrm {Ray}_x(\mathcal {D}_0,\eta )\subset \mathrm {Ray}_x(\mathcal {D},\eta )$
as in Remark 3.13(d) and can talk about the
$\mathrm {Ray}_x(\mathcal {D}_0,\eta )\subset \mathrm {Ray}_x(\mathcal {D},\eta )$
as in Remark 3.13(d) and can talk about the
 $(\mathcal {D},\eta ;N)$
-equivalence of
$(\mathcal {D},\eta ;N)$
-equivalence of
 $(\mathcal {D}_0,\eta )$
-rays.
$(\mathcal {D}_0,\eta )$
-rays.
We are now ready to define the meandering hyperbolicity condition. First, we recall the notion of S-hyperbolicity which Sullivan defined in [Reference Sullivan35].
Definition 3.25 (S-hyperbolicity)
Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
.
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
.
-
(a) The action
 $\rho $
is said to be S-hyperbolic (at
$\rho $
is said to be S-hyperbolic (at
 $\Lambda $
) if there exists an integer
$\Lambda $
) if there exists an integer
 $N\ge 1$
such that, for every
$N\ge 1$
such that, for every
 $x\in \Lambda $
, all rays in
$x\in \Lambda $
, all rays in
 $\mathrm {Ray}_x(\mathcal {D},\delta )$
are
$\mathrm {Ray}_x(\mathcal {D},\delta )$
are
 $(\mathcal {D},\delta ;N)$
-fellow-traveling.
$(\mathcal {D},\delta ;N)$
-fellow-traveling. -
(b) The action
 $\rho $
is said to be uniformly S-hyperbolic (at
$\rho $
is said to be uniformly S-hyperbolic (at
 $\Lambda $
) if there is an integer
$\Lambda $
) if there is an integer
 $N \ge 1$
such that, for every
$N \ge 1$
such that, for every
 $\eta \in (0,\delta ]$
and every
$\eta \in (0,\delta ]$
and every
 $x\in \Lambda $
, all rays in
$x\in \Lambda $
, all rays in
 $\mathrm {Ray}_x(\mathcal {D},\eta )$
are
$\mathrm {Ray}_x(\mathcal {D},\eta )$
are
 $(\mathcal {D},\eta ;N)$
-fellow-traveling.
$(\mathcal {D},\eta ;N)$
-fellow-traveling.
We shall refer to the pair
![]() $(\mathcal {D};N)$
as a (uniform) S-hyperbolicity datum of
$(\mathcal {D};N)$
as a (uniform) S-hyperbolicity datum of
![]() $\rho $
.
$\rho $
.
By weakening the
![]() $(\mathcal {D},\eta ;N)$
-fellow-traveling condition in the definition of S-hyperbolicity to the
$(\mathcal {D},\eta ;N)$
-fellow-traveling condition in the definition of S-hyperbolicity to the
![]() $(\mathcal {D},\eta ;N)$
-equivalence, as well as considering a refined expansion datum (Definition 3.7), we define the notion of meandering hyperbolicity as follows.
$(\mathcal {D},\eta ;N)$
-equivalence, as well as considering a refined expansion datum (Definition 3.7), we define the notion of meandering hyperbolicity as follows.
Definition 3.26 (Meandering hyperbolicity)
Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with the expansion datum
$\Lambda $
with the expansion datum
![]() $\mathcal {D}_0=(\mathcal {I}_0,\mathcal {U}_0,\varSigma _0, \delta _0,L_0,\lambda _0)$
.
$\mathcal {D}_0=(\mathcal {I}_0,\mathcal {U}_0,\varSigma _0, \delta _0,L_0,\lambda _0)$
.
-
(a) The action
 $\rho $
is said to be meandering-hyperbolic (at
$\rho $
is said to be meandering-hyperbolic (at
 $\Lambda $
) if there exist a refinement
$\Lambda $
) if there exist a refinement
 $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )\succ \mathcal {D}_0$
and an integer
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )\succ \mathcal {D}_0$
and an integer
 $N\ge 1$
such that, for every
$N\ge 1$
such that, for every
 $x\in \Lambda $
, all rays in
$x\in \Lambda $
, all rays in
 $\mathrm {Ray}_x(\mathcal {D}_0,\delta _0)$
are
$\mathrm {Ray}_x(\mathcal {D}_0,\delta _0)$
are
 $(\mathcal {D},\delta ;N)$
-equivalent (as rays in
$(\mathcal {D},\delta ;N)$
-equivalent (as rays in
 $\mathrm {Ray}_x(\mathcal {D},\delta )$
).
$\mathrm {Ray}_x(\mathcal {D},\delta )$
). -
(b) The action
 $\rho $
is said to be uniformly meandering-hyperbolic (at
$\rho $
is said to be uniformly meandering-hyperbolic (at
 $\Lambda $
) if there are a refinement
$\Lambda $
) if there are a refinement
 $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )\succ \mathcal {D}_0$
and an integer
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )\succ \mathcal {D}_0$
and an integer
 $N\ge 1$
such that, for every
$N\ge 1$
such that, for every
 $\eta \in (0,\delta ]$
and every
$\eta \in (0,\delta ]$
and every
 $x\in \Lambda $
, all rays in
$x\in \Lambda $
, all rays in
 $\mathrm {Ray}_x(\mathcal {D}_0,\eta )$
are
$\mathrm {Ray}_x(\mathcal {D}_0,\eta )$
are
 $(\mathcal {D},\eta ;N)$
-equivalent (as rays in
$(\mathcal {D},\eta ;N)$
-equivalent (as rays in
 $\mathrm {Ray}_x(\mathcal {D},\eta )$
).
$\mathrm {Ray}_x(\mathcal {D},\eta )$
).
We shall refer to the triple
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
as a (uniform) meandering hyperbolicity datum of
$(\mathcal {D}_0\prec \mathcal {D};N)$
as a (uniform) meandering hyperbolicity datum of
![]() $\rho $
.
$\rho $
.
Remark 3.27.
-
(a) Obviously, uniform meandering hyperbolicity implies meandering hyperbolicity.
-
(b) If an action is S-hyperbolic with a datum
 $(\mathcal {D}_0;N)$
, then, for any trivial refinement
$(\mathcal {D}_0;N)$
, then, for any trivial refinement
 $\mathcal {D}$
of
$\mathcal {D}$
of
 $\mathcal {D}_0$
(see Definition 3.8), it is meandering-hyperbolic with the datum
$\mathcal {D}_0$
(see Definition 3.8), it is meandering-hyperbolic with the datum
 $(\mathcal {D}_0\prec \mathcal {D};N)$
since
$(\mathcal {D}_0\prec \mathcal {D};N)$
since
 $(\mathcal {D}_0,\eta ;N)$
-fellow-traveling rays are
$(\mathcal {D}_0,\eta ;N)$
-fellow-traveling rays are
 $(\mathcal {D},\eta ;N)$
-equivalent.
$(\mathcal {D},\eta ;N)$
-equivalent. -
(c) A prime example of a meandering-hyperbolic action which is not S-hyperbolic is given by uniform lattices in higher rank semisimple Lie groups (see Section 5). All other examples of meandering-hyperbolic actions we present in this paper are actually S-hyperbolic (see Sections 3.2, 6 and 7).
-
(d) We exhibit expanding actions which fail to be meandering-hyperbolic in Section 7.1.
4 The structural stability theorem
In Section 4.1, we present the statement of our structural stability theorem for meandering-hyperbolic actions. Then we devote the rest of the section to its proof.
4.1 Statement of the theorem: Meandering hyperbolicity implies stability
Suppose
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
![]() $\Lambda $
. Following Sullivan’s remark (at the very end of his paper [Reference Sullivan35]), we would like to talk about small perturbations of
$\Lambda $
. Following Sullivan’s remark (at the very end of his paper [Reference Sullivan35]), we would like to talk about small perturbations of
![]() $\rho $
which are still expanding. For this, we only need information on a neighborhood of the compact subset
$\rho $
which are still expanding. For this, we only need information on a neighborhood of the compact subset
![]() $\Lambda $
.
$\Lambda $
.
We equip
![]() $\mathrm {LHomeo}(M)$
with what we call the compact-open Lipschitz topology. Given a compact subset
$\mathrm {LHomeo}(M)$
with what we call the compact-open Lipschitz topology. Given a compact subset
![]() $K\subset M$
, a positive number
$K\subset M$
, a positive number
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $f\in \mathrm {LHomeo}(M)$
, let
$f\in \mathrm {LHomeo}(M)$
, let
![]() $U(f;K,\epsilon )$
denote the set of all
$U(f;K,\epsilon )$
denote the set of all
![]() $g\in \mathrm {LHomeo}(M)$
that are
$g\in \mathrm {LHomeo}(M)$
that are
![]() $\epsilon $
-close to f on K with respect to the metric
$\epsilon $
-close to f on K with respect to the metric
![]() $d_{\mathrm {Lip},K}$
defined by
$d_{\mathrm {Lip},K}$
defined by
 $$ \begin{align} d_{\mathrm{Lip},K}(f,g):= \sup_{x\in K} d(f(x),g(x))+ \sup_{\substack{x,y\in K \\ x\neq y}} \left|\frac{d(f(x),f(y))}{d(x,y)}-\frac{d(g(x),g(y))}{d(x,y)}\right| <\epsilon. \end{align} $$
$$ \begin{align} d_{\mathrm{Lip},K}(f,g):= \sup_{x\in K} d(f(x),g(x))+ \sup_{\substack{x,y\in K \\ x\neq y}} \left|\frac{d(f(x),f(y))}{d(x,y)}-\frac{d(g(x),g(y))}{d(x,y)}\right| <\epsilon. \end{align} $$
We define the compact-open Lipschitz topology on
![]() $\mathrm {LHomeo}(M)$
as the topology generated by the collection of all such
$\mathrm {LHomeo}(M)$
as the topology generated by the collection of all such
![]() $U(f;K,\epsilon )$
. This topology enables us to control the image as well as the Lipschitz constant on a neighborhood of the compact subset
$U(f;K,\epsilon )$
. This topology enables us to control the image as well as the Lipschitz constant on a neighborhood of the compact subset
![]() $\Lambda $
.
$\Lambda $
.
Remark 4.2. As we mentioned in the introduction, Sullivan [Reference Sullivan35, §9] actually considers the case when M is a Riemannian manifold with the Riemannian distance function d and the actions are by
![]() $C^1$
-diffeomorphisms. In this case, the compact-open Lipschitz topology on
$C^1$
-diffeomorphisms. In this case, the compact-open Lipschitz topology on
![]() $\mathrm {Diff}^1(M)$
is weaker than the compact-open
$\mathrm {Diff}^1(M)$
is weaker than the compact-open
![]() $C^1$
-topology.
$C^1$
-topology.
Suppose
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\mathcal {I},\varSigma )$
(Definition 3.4). Given a compact subset
$\mathcal {D}=(\mathcal {I},\varSigma )$
(Definition 3.4). Given a compact subset
![]() $K\subset M$
and
$K\subset M$
and
![]() $\epsilon>0$
, we say that a homomorphism
$\epsilon>0$
, we say that a homomorphism
![]() $\rho ':\Gamma \to \mathrm {LHomeo}(M)$
is a
$\rho ':\Gamma \to \mathrm {LHomeo}(M)$
is a
![]() $(K,\epsilon )$
-perturbation of
$(K,\epsilon )$
-perturbation of
![]() $\rho $
if
$\rho $
if
![]() $\rho '(s_i)$
is
$\rho '(s_i)$
is
![]() $\epsilon $
-close to
$\epsilon $
-close to
![]() $\rho (s_i)$
on K for all
$\rho (s_i)$
on K for all
![]() $i\in \mathcal {I}$
. The set of all
$i\in \mathcal {I}$
. The set of all
![]() $(K,\epsilon )$
-perturbations of
$(K,\epsilon )$
-perturbations of
![]() $\rho $
will be denoted by
$\rho $
will be denoted by
Accordingly, we topologize
![]() $\mathrm {Hom}(\Gamma ,\mathrm {LHomeo}(M))$
via the topology of ‘algebraic convergence’ by identifying it, via the map
$\mathrm {Hom}(\Gamma ,\mathrm {LHomeo}(M))$
via the topology of ‘algebraic convergence’ by identifying it, via the map
![]() $\rho \mapsto (\rho (s_i))_{i\in \mathcal {I}}$
, with a subset of
$\rho \mapsto (\rho (s_i))_{i\in \mathcal {I}}$
, with a subset of
![]() $[\mathrm {LHomeo}(M)]^{\mathcal {I}}$
equipped with the subspace topology. Then the subset
$[\mathrm {LHomeo}(M)]^{\mathcal {I}}$
equipped with the subspace topology. Then the subset
![]() $U(\rho ;K,\epsilon )$
of
$U(\rho ;K,\epsilon )$
of
![]() $\mathrm {Hom}(\Gamma ,\mathrm {LHomeo}(M))$
is an open neighborhood of
$\mathrm {Hom}(\Gamma ,\mathrm {LHomeo}(M))$
is an open neighborhood of
![]() $\rho $
. Note that, when the ambient space M itself is compact, we can set
$\rho $
. Note that, when the ambient space M itself is compact, we can set
![]() $K=M$
and simply talk about
$K=M$
and simply talk about
![]() $\epsilon $
-perturbations.
$\epsilon $
-perturbations.
Now, we are able to state our structural stability theorem for meandering-hyperbolic actions.
Theorem 4.4. If an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is meandering-hyperbolic at a compact invariant subset
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is meandering-hyperbolic at a compact invariant subset
![]() $\Lambda \subset M$
with a datum
$\Lambda \subset M$
with a datum
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
, then the following hold.
$(\mathcal {D}_0\prec \mathcal {D};N)$
, then the following hold.
-
(1) The action
 $\rho $
is structurally stable in the sense of Lipschitz dynamics. In other words, there exist a compact set
$\rho $
is structurally stable in the sense of Lipschitz dynamics. In other words, there exist a compact set
 $K\supset \Lambda $
and a constant
$K\supset \Lambda $
and a constant
 $\epsilon =\epsilon (\mathcal {D},N)>0$
such that for every there exist a
$\epsilon =\epsilon (\mathcal {D},N)>0$
such that for every there exist a $$\begin{align*}\rho'\in U(\rho;K,\epsilon) \end{align*}$$
$$\begin{align*}\rho'\in U(\rho;K,\epsilon) \end{align*}$$
 $\rho '$
-invariant compact subset
$\rho '$
-invariant compact subset
 $\Lambda '\subset M$
and an equivariant homeomorphism that is,
$\Lambda '\subset M$
and an equivariant homeomorphism that is, $$\begin{align*}\phi:\Lambda\to\Lambda', \end{align*}$$
$$\begin{align*}\phi:\Lambda\to\Lambda', \end{align*}$$
 $\rho '(g)\circ \phi =\phi \circ \rho (g)$
on
$\rho '(g)\circ \phi =\phi \circ \rho (g)$
on
 $\Lambda $
for all
$\Lambda $
for all
 $g\in \Gamma $
.
$g\in \Gamma $
.
-
(2) The map
 $U(\rho ;K,\epsilon )\to C^0(\Lambda , M)$
,
$U(\rho ;K,\epsilon )\to C^0(\Lambda , M)$
,
 $\rho '\mapsto \phi $
is continuous at
$\rho '\mapsto \phi $
is continuous at
 $\rho $
.
$\rho $
. -
(3) Every action
 $\rho '\in U(\rho ;K,\epsilon )$
is expanding at
$\rho '\in U(\rho ;K,\epsilon )$
is expanding at
 $\Lambda '$
.
$\Lambda '$
.
If an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is uniformly meandering-hyperbolic, then, in addition to the preceding statements, the following is true as well.
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is uniformly meandering-hyperbolic, then, in addition to the preceding statements, the following is true as well.
-
(4) Every action
 $\rho '\in U(\rho ;K,\epsilon )$
is again uniformly meandering-hyperbolic.
$\rho '\in U(\rho ;K,\epsilon )$
is again uniformly meandering-hyperbolic.
As an immediate consequence of Theorem 4.4(1), we have:
Corollary 4.5. A meandering-hyperbolic action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
at a compact invariant subset
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
at a compact invariant subset
![]() $\Lambda \subset M$
is algebraically stable in the following sense: For every
$\Lambda \subset M$
is algebraically stable in the following sense: For every
![]() $\rho '\in U(\rho ;K,\epsilon )$
, the kernel of the
$\rho '\in U(\rho ;K,\epsilon )$
, the kernel of the
![]() $\rho '$
-action on
$\rho '$
-action on
![]() $\Lambda '$
equals the kernel of the
$\Lambda '$
equals the kernel of the
![]() $\rho $
-action on
$\rho $
-action on
![]() $\Lambda $
.
$\Lambda $
.
We note, however, that faithfulness of the
![]() $\rho $
-action on M does not imply faithfulness of nearby actions: See Example 7.7.
$\rho $
-action on M does not imply faithfulness of nearby actions: See Example 7.7.
In view of Remarks 3.6(c), 3.27(b) and 4.2, we obtain Sullivan’s structural stability theorem [Reference Sullivan35, Theorem II] in the
![]() $C^1$
-setting as a corollary of Theorem 4.4(1):
$C^1$
-setting as a corollary of Theorem 4.4(1):
Corollary 4.6. Consider a group action
![]() $\Gamma \to \mathrm {Diff}^1(M)$
on a Riemannian manifold M with a compact invariant subset
$\Gamma \to \mathrm {Diff}^1(M)$
on a Riemannian manifold M with a compact invariant subset
![]() $\Lambda \subset M$
. If the action is S-hyperbolic, then it is structurally stable in the sense of
$\Lambda \subset M$
. If the action is S-hyperbolic, then it is structurally stable in the sense of
![]() $C^1$
-dynamics.
$C^1$
-dynamics.
Remark 4.7. Sullivan’s structural stability theorem stated above is not to be confused with the main theorem of [Reference Sullivan35], which is widely known in the theory of Kleinian groups. In order to guide the reader, we summarize the contents of Sullivan’s paper [Reference Sullivan35] as follows.
Let
![]() $\Gamma <\mathrm {PSL}(2,\mathbb {C})$
be a finitely generated, nonsolvable, nonrigid, nonrelatively-compact and torsion-free group of conformal transformations of the Riemann sphere
$\Gamma <\mathrm {PSL}(2,\mathbb {C})$
be a finitely generated, nonsolvable, nonrigid, nonrelatively-compact and torsion-free group of conformal transformations of the Riemann sphere
![]() $P^1(\mathbb {C})$
. Sullivan showed that the following are equivalent:
$P^1(\mathbb {C})$
. Sullivan showed that the following are equivalent:
-
(1) the subgroup
 $\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is convex-cocompact;
$\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is convex-cocompact; -
(2) the
 $\Gamma $
-action on the limit set
$\Gamma $
-action on the limit set
 $\Lambda \subset P^1(\mathbb {C})$
satisfies the expansion-hyperbolicity axioms;
$\Lambda \subset P^1(\mathbb {C})$
satisfies the expansion-hyperbolicity axioms; -
(3) this action is structurally stable in the sense of
 $C^1$
-dynamics;
$C^1$
-dynamics; -
(4) the subgroup
 $\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is algebraically stable.
$\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is algebraically stable.
Here,
![]() $\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is said to be algebraically stable if all representations
$\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is said to be algebraically stable if all representations
![]() $\Gamma \to \mathrm {PSL}(2,\mathbb {C})$
sufficiently close to the identity embedding are injective.
$\Gamma \to \mathrm {PSL}(2,\mathbb {C})$
sufficiently close to the identity embedding are injective.
The implication (4
![]() $\Rightarrow $
1) is the main result (Theorem A) of the paper [Reference Sullivan35], in the proof of which his quasi-conformal stability theorem (Theorem C) is obtained. The implication (1
$\Rightarrow $
1) is the main result (Theorem A) of the paper [Reference Sullivan35], in the proof of which his quasi-conformal stability theorem (Theorem C) is obtained. The implication (1
![]() $\Rightarrow $
2) is his Theorem I, (2
$\Rightarrow $
2) is his Theorem I, (2
![]() $\Rightarrow $
3) is a special case of Theorem II, and (3
$\Rightarrow $
3) is a special case of Theorem II, and (3
![]() $\Rightarrow $
4) is immediate. For groups with torsion, the implication (4
$\Rightarrow $
4) is immediate. For groups with torsion, the implication (4
![]() $\Rightarrow $
1) is false (see Example 7.12) but the other implications (1
$\Rightarrow $
1) is false (see Example 7.12) but the other implications (1
![]() $\Rightarrow $
2
$\Rightarrow $
2
![]() $\Rightarrow $
3
$\Rightarrow $
3
![]() $\Rightarrow $
4) still hold.
$\Rightarrow $
4) still hold.
4.2 Specifying small perturbations
 $\rho '$
$\rho '$
We now proceed to prove Theorem 4.4. The assertion (1) will be proved in Sections 4.2–4.7, and the assertions (2)-(4) in Sections 4.8–4.10, respectively.
Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be a meandering-hyperbolic action (Definition 3.26) at a compact invariant subset
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be a meandering-hyperbolic action (Definition 3.26) at a compact invariant subset
![]() $\Lambda \subset M$
with a datum
$\Lambda \subset M$
with a datum
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
, where
$(\mathcal {D}_0\prec \mathcal {D};N)$
, where
 $$ \begin{align*} (\mathcal{I}_0,\mathcal{U}_0,\varSigma_0,\delta_0,L_0,\lambda_0)=\mathcal{D}_0\prec\mathcal{D}=(\mathcal{I},\mathcal{U},\varSigma,\delta,L,\lambda),\\ \mathrm{that \ is,} \ \mathcal{I}_0\subset\mathcal{I},\; \mathcal{U}_0\prec\mathcal{U},\; \varSigma_0\prec\varSigma,\; \delta_0>\delta,\; L_0\le L,\; \lambda_0\ge\lambda. \end{align*} $$
$$ \begin{align*} (\mathcal{I}_0,\mathcal{U}_0,\varSigma_0,\delta_0,L_0,\lambda_0)=\mathcal{D}_0\prec\mathcal{D}=(\mathcal{I},\mathcal{U},\varSigma,\delta,L,\lambda),\\ \mathrm{that \ is,} \ \mathcal{I}_0\subset\mathcal{I},\; \mathcal{U}_0\prec\mathcal{U},\; \varSigma_0\prec\varSigma,\; \delta_0>\delta,\; L_0\le L,\; \lambda_0\ge\lambda. \end{align*} $$
Recall, in particular, that
![]() $\rho $
is expanding with respect to the refined datum
$\rho $
is expanding with respect to the refined datum
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
For convenience, we summarize all the important constants for the proof as follows:

The compact set
![]() $K\supset \Lambda $
and the constant
$K\supset \Lambda $
and the constant
![]() $\epsilon =\epsilon (\mathcal {D},N)>0$
specify the open set
$\epsilon =\epsilon (\mathcal {D},N)>0$
specify the open set
![]() $U(\rho ;K,\epsilon )$
of all
$U(\rho ;K,\epsilon )$
of all
![]() $(K,\epsilon )$
-perturbations
$(K,\epsilon )$
-perturbations
![]() $\rho '$
of
$\rho '$
of
![]() $\rho $
. Note that K is compact since
$\rho $
. Note that K is compact since
![]() $(M,d)$
is assumed to be proper. Since
$(M,d)$
is assumed to be proper. Since
![]() $\delta \le \delta _{\mathcal {U}}$
is a Lebesgue number of
$\delta \le \delta _{\mathcal {U}}$
is a Lebesgue number of
![]() $\mathcal {U}$
, it follows that
$\mathcal {U}$
, it follows that
![]() $\mathcal {U}$
is a cover of
$\mathcal {U}$
is a cover of
![]() $N_{\delta }(\Lambda )$
.
$N_{\delta }(\Lambda )$
.
Now, we suppose
Then, by the definitions (4.1) and (4.3), we have that for all
![]() $s\in \varSigma $
,
$s\in \varSigma $
,
We first observe that for each
![]() $i\in \mathcal {I}$
,
$i\in \mathcal {I}$
,
Indeed, since
![]() $\rho (s_i^{-1})$
is
$\rho (s_i^{-1})$
is
![]() $\lambda $
-expanding on
$\lambda $
-expanding on
![]() $U_i$
, we see from equation (4.8) that for all distinct
$U_i$
, we see from equation (4.8) that for all distinct
![]() $x,y\in U_i\cap K$
,
$x,y\in U_i\cap K$
,
 $$ \begin{align*} \frac{d(\rho'(s_i^{-1})(x),\rho'(s_i^{-1})(y))}{d(x,y)}>\frac{d(\rho(s_i^{-1})(x),\rho(s_i^{-1})(y))}{d(x,y)}-\epsilon \ge \lambda-\epsilon =\lambda'. \end{align*} $$
$$ \begin{align*} \frac{d(\rho'(s_i^{-1})(x),\rho'(s_i^{-1})(y))}{d(x,y)}>\frac{d(\rho(s_i^{-1})(x),\rho(s_i^{-1})(y))}{d(x,y)}-\epsilon \ge \lambda-\epsilon =\lambda'. \end{align*} $$
Moreover, we also note that
for every
![]() $i\in \mathcal {I}$
. To see this, recall that the maps
$i\in \mathcal {I}$
. To see this, recall that the maps
![]() $\rho (s_i)$
are L-Lipschitz on
$\rho (s_i)$
are L-Lipschitz on
![]() $N_{\delta }(\Lambda )$
by Definition 3.4(i), thus by equation (4.8) again
$N_{\delta }(\Lambda )$
by Definition 3.4(i), thus by equation (4.8) again
 $$ \begin{align*} \frac{d(\rho'(s_i)(x),\rho'(s_i)(y))}{d(x,y)} <\frac{d(\rho(s_i)(x),\rho(s_i)(y))}{d(x,y)}+\epsilon \le L+\epsilon=L' \end{align*} $$
$$ \begin{align*} \frac{d(\rho'(s_i)(x),\rho'(s_i)(y))}{d(x,y)} <\frac{d(\rho(s_i)(x),\rho(s_i)(y))}{d(x,y)}+\epsilon \le L+\epsilon=L' \end{align*} $$
for all distinct
![]() $x,y\in N_{\delta }(\Lambda )\subset K$
. Note that
$x,y\in N_{\delta }(\Lambda )\subset K$
. Note that
![]() $L'=L+\epsilon \ge \lambda +\epsilon>\lambda -\epsilon =\lambda '$
.
$L'=L+\epsilon \ge \lambda +\epsilon>\lambda -\epsilon =\lambda '$
.
For later use, we prove the following lemma.
Lemma 4.11. For every
![]() $w\in \Gamma $
such that
$w\in \Gamma $
such that
![]() $|w|_{\varSigma }=n\le N$
, we have
$|w|_{\varSigma }=n\le N$
, we have
for all
![]() $y\in N_{\kappa } (\Lambda )$
.
$y\in N_{\kappa } (\Lambda )$
.
Proof. We prove this by induction on
![]() $n\leq N$
. If
$n\leq N$
. If
![]() $|w|_{\varSigma }=1$
, the claim is true by equation (4.8) since
$|w|_{\varSigma }=1$
, the claim is true by equation (4.8) since
![]() $N_{\kappa }(\Lambda )\subset N_{\delta }(\Lambda )$
. Suppose
$N_{\kappa }(\Lambda )\subset N_{\delta }(\Lambda )$
. Suppose
![]() $w=st$
with
$w=st$
with
![]() $s\in \varSigma $
,
$s\in \varSigma $
,
![]() $|t|_{\varSigma }=n-1$
and
$|t|_{\varSigma }=n-1$
and
![]() $|w|_{\varSigma }=n$
. Since
$|w|_{\varSigma }=n$
. Since
![]() $\rho (t)$
is
$\rho (t)$
is
![]() $L^{n-1}$
-Lipschitz on
$L^{n-1}$
-Lipschitz on
![]() $N_{\delta /L^{n-2}}(\Lambda )\supset N_{\kappa }(\Lambda )$
by equation (3.5), we have
$N_{\delta /L^{n-2}}(\Lambda )\supset N_{\kappa }(\Lambda )$
by equation (3.5), we have
![]() $\rho (t)(y)\in N_{L^{n-1}\kappa }(\Lambda )\subset N_{\delta }(\Lambda )$
. By the induction hypothesis
$\rho (t)(y)\in N_{L^{n-1}\kappa }(\Lambda )\subset N_{\delta }(\Lambda )$
. By the induction hypothesis
![]() $d(\rho (t)(y),\rho '(t)(y))<(n-1)L^{n-2}\epsilon $
, we then have
$d(\rho (t)(y),\rho '(t)(y))<(n-1)L^{n-2}\epsilon $
, we then have
![]() $\rho '(t)(y)\in N_{\delta }(\Lambda )$
as well, since
$\rho '(t)(y)\in N_{\delta }(\Lambda )$
as well, since
![]() $\epsilon =\frac {\lambda -1}{2}\kappa <L\kappa $
and thus
$\epsilon =\frac {\lambda -1}{2}\kappa <L\kappa $
and thus
As
![]() $\rho (s)$
is L-Lipschitz on
$\rho (s)$
is L-Lipschitz on
![]() $N_{\delta }(\Lambda )$
, we obtain
$N_{\delta }(\Lambda )$
, we obtain
Furthermore, we have from equation (4.8)
since
![]() $\rho '(t)(y)\in N_{\delta }(\Lambda )$
. Thus,
$\rho '(t)(y)\in N_{\delta }(\Lambda )$
. Thus,
 $$ \begin{align*} d(\rho(w)(y),\rho'(w)(y)) &\le d\big(\rho(s)[\rho(t)(y)],\rho(s)[\rho'(t)(y)]\big) +d\big(\rho(s)[\rho'(t)(y)],\rho'(s)[\rho'(t)(y)]\big)\\ &< (n-1)L^{n-1}\epsilon + \epsilon\\ &< (n-1)L^{n-1}\epsilon + L^{n-1}\epsilon = nL^{n-1}\epsilon, \end{align*} $$
$$ \begin{align*} d(\rho(w)(y),\rho'(w)(y)) &\le d\big(\rho(s)[\rho(t)(y)],\rho(s)[\rho'(t)(y)]\big) +d\big(\rho(s)[\rho'(t)(y)],\rho'(s)[\rho'(t)(y)]\big)\\ &< (n-1)L^{n-1}\epsilon + \epsilon\\ &< (n-1)L^{n-1}\epsilon + L^{n-1}\epsilon = nL^{n-1}\epsilon, \end{align*} $$
and the claim is proved.
4.3 Definition of
 $\phi $
$\phi $
We first construct a map
![]() $\phi :\Lambda \to M$
.
$\phi :\Lambda \to M$
.
Let
![]() $x\in \Lambda $
. In order to define
$x\in \Lambda $
. In order to define
![]() $\phi (x)$
, choose a
$\phi (x)$
, choose a
![]() $(\mathcal {D}_0,\delta _0)$
-code
$(\mathcal {D}_0,\delta _0)$
-code
![]() $(\alpha ,p)$
for x as in Section 3.3. Since
$(\alpha ,p)$
for x as in Section 3.3. Since
![]() $\delta <\delta _0$
, we may regard
$\delta <\delta _0$
, we may regard
![]() $\alpha $
as a
$\alpha $
as a
![]() $(\mathcal {D},\delta )$
-code as in Remark 3.11(c)(d). Then, as we know from Lemma 3.14, the point x has an exponentially shrinking nested sequence of neighborhoods
$(\mathcal {D},\delta )$
-code as in Remark 3.11(c)(d). Then, as we know from Lemma 3.14, the point x has an exponentially shrinking nested sequence of neighborhoods
![]() $\rho (c^{\alpha }_k)[B_{\delta }(p_{k+1})]$
(
$\rho (c^{\alpha }_k)[B_{\delta }(p_{k+1})]$
(
![]() $k\in \mathbb {N}_0$
) such that
$k\in \mathbb {N}_0$
) such that
 $$\begin{align*}\{x\}=\bigcap_{k=0}^{\infty}\rho(c^{\alpha}_k)[B_{\delta}(p_{k+1})]. \end{align*}$$
$$\begin{align*}\{x\}=\bigcap_{k=0}^{\infty}\rho(c^{\alpha}_k)[B_{\delta}(p_{k+1})]. \end{align*}$$
Now, consider a perturbation
![]() $\rho '\in U(\rho ;K,\epsilon )$
of
$\rho '\in U(\rho ;K,\epsilon )$
of
![]() $\rho $
as specified in Section 4.2. We claim that the sequence of perturbed subsets
$\rho $
as specified in Section 4.2. We claim that the sequence of perturbed subsets
![]() $\rho '(c^{\alpha }_k)[B_{\delta }(p_{k})]$
(
$\rho '(c^{\alpha }_k)[B_{\delta }(p_{k})]$
(
![]() $k\in \mathbb {N}_0$
) is also nested and exponentially shrinking. Since M is complete, the intersection of this collection of subsets is a singleton in M and we can define
$k\in \mathbb {N}_0$
) is also nested and exponentially shrinking. Since M is complete, the intersection of this collection of subsets is a singleton in M and we can define
![]() $\phi _{\alpha }(x)$
by the formula
$\phi _{\alpha }(x)$
by the formula
 $$ \begin{align*} \{\phi_{\alpha}(x)\} =\bigcap_{k=0}^{\infty}\rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})]. \end{align*} $$
$$ \begin{align*} \{\phi_{\alpha}(x)\} =\bigcap_{k=0}^{\infty}\rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})]. \end{align*} $$
The claim will be proved in the following lemma, where, in fact, we shall find the values of
![]() $\eta \le \delta $
for which the sequence
$\eta \le \delta $
for which the sequence
![]() $\rho '(c^{\alpha }_k)[B_{\eta }(p_{k})]$
is nested and exponentially shrinking. This lemma will later be used often, for example, when we show that
$\rho '(c^{\alpha }_k)[B_{\eta }(p_{k})]$
is nested and exponentially shrinking. This lemma will later be used often, for example, when we show that
![]() $\phi $
is well-defined (Section 4.4) and is continuous (Section 4.6).
$\phi $
is well-defined (Section 4.4) and is continuous (Section 4.6).
Lemma 4.12. Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be a meandering-hyperbolic action with the datum
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be a meandering-hyperbolic action with the datum
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
. Consider a number
$(\mathcal {D}_0\prec \mathcal {D};N)$
. Consider a number
![]() $0<t\le \kappa =\min \{\frac {\delta }{(N+1)L^N},1\}$
(so that
$0<t\le \kappa =\min \{\frac {\delta }{(N+1)L^N},1\}$
(so that
![]() $\frac {\lambda -1}{2}t\le \epsilon $
), and let
$\frac {\lambda -1}{2}t\le \epsilon $
), and let
If
![]() $(\alpha ,p)$
is a
$(\alpha ,p)$
is a
![]() $(\mathcal {D},\delta )$
-code for
$(\mathcal {D},\delta )$
-code for
![]() $x\in \Lambda $
, then for every
$x\in \Lambda $
, then for every
![]() $\eta \in [t,\delta ]$
the sequence of subsets
$\eta \in [t,\delta ]$
the sequence of subsets
is nested and exponentially shrinking. Consequently, we have
 $$ \begin{align*} \{\phi_{\alpha}(x)\} =\bigcap_{k=0}^{\infty}\rho'(c^{\alpha}_k)[B_{\eta}(p_{k+1})] =\bigcap_{k=0}^{\infty}\rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})] \end{align*} $$
$$ \begin{align*} \{\phi_{\alpha}(x)\} =\bigcap_{k=0}^{\infty}\rho'(c^{\alpha}_k)[B_{\eta}(p_{k+1})] =\bigcap_{k=0}^{\infty}\rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})] \end{align*} $$
and thus, for every
![]() $k\in \mathbb {N}_0$
,
$k\in \mathbb {N}_0$
,
If the
![]() $\delta $
-code
$\delta $
-code
![]() $(\alpha ,p)$
is special, then
$(\alpha ,p)$
is special, then
Proof. Since
![]() $t\le \eta $
, we see from the assumption
$t\le \eta $
, we see from the assumption
![]() $\rho '\in U(\rho ;K,\frac {\lambda -1}{2}t)$
that
$\rho '\in U(\rho ;K,\frac {\lambda -1}{2}t)$
that
for all
![]() $i\in \mathcal {I}$
. Since
$i\in \mathcal {I}$
. Since
![]() $\eta \le \delta $
, we have by Definition 3.4(ii) the inclusion (3.15) for
$\eta \le \delta $
, we have by Definition 3.4(ii) the inclusion (3.15) for
![]() $\rho $
$\rho $
for all
![]() $k\in \mathbb {N}$
, while
$k\in \mathbb {N}$
, while
![]() $B_{\eta }(p_k)\subset B_{\delta }(p_k)\subset U_{\alpha (k)}\cap K$
as
$B_{\eta }(p_k)\subset B_{\delta }(p_k)\subset U_{\alpha (k)}\cap K$
as
![]() $\alpha $
is a
$\alpha $
is a
![]() $\delta $
-code.
$\delta $
-code.
In particular, we see from equation (4.14) that the boundary of
![]() $\rho (s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
lies outside
$\rho (s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
lies outside
![]() $B_{\lambda \eta }(p_{k+1})$
, and from equation (4.13) that the boundary of
$B_{\lambda \eta }(p_{k+1})$
, and from equation (4.13) that the boundary of
![]() $\rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
lies outside the ball centered at
$\rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
lies outside the ball centered at
![]() $p_{k+1}$
of radius
$p_{k+1}$
of radius
![]() $\lambda \eta -\frac {1}{2}(\lambda \eta -\eta )=\frac {1}{2}\eta (\lambda +1)>\eta $
. Moreover,
$\lambda \eta -\frac {1}{2}(\lambda \eta -\eta )=\frac {1}{2}\eta (\lambda +1)>\eta $
. Moreover,
![]() $\rho '(s_{\alpha (k)}^{-1})(p_k)$
lies in the ball centered at
$\rho '(s_{\alpha (k)}^{-1})(p_k)$
lies in the ball centered at
![]() $p_{k+1}$
of radius
$p_{k+1}$
of radius
![]() $\frac {1}{2}\eta (\lambda -1)$
, which implies
$\frac {1}{2}\eta (\lambda -1)$
, which implies
![]() $\rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]\cap B_{\frac {1}{2}\eta (\lambda +1)}(p_{k+1})\neq \emptyset $
. Note that every open ball is path-connected in a geodesic metric space M. Thus, we deduce that
$\rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]\cap B_{\frac {1}{2}\eta (\lambda +1)}(p_{k+1})\neq \emptyset $
. Note that every open ball is path-connected in a geodesic metric space M. Thus, we deduce that
![]() $\rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
is a connected component of
$\rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
is a connected component of
![]() $M\setminus \partial \rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
and hence
$M\setminus \partial \rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
and hence
![]() $B_{\frac {1}{2}\eta (\lambda +1)}(p_{k+1})\subset \rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
. Therefore, we conclude that
$B_{\frac {1}{2}\eta (\lambda +1)}(p_{k+1})\subset \rho '(s_{\alpha (k)}^{-1})[B_{\eta }(p_k)]$
. Therefore, we conclude that
Thus,
for all
![]() $k\in \mathbb {N}$
, and we check as in equation (3.18) the nesting property
$k\in \mathbb {N}$
, and we check as in equation (3.18) the nesting property
for all
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
Furthermore, the diameter of
![]() $ \rho '(c^{\alpha }_k)[B_{\eta }(p_{k+1})] =\rho '(s_{\alpha (0)}s_{\alpha (1)}\cdots s_{\alpha (k)})[B_{\eta }(p_{k+1})]$
is at most
$ \rho '(c^{\alpha }_k)[B_{\eta }(p_{k+1})] =\rho '(s_{\alpha (0)}s_{\alpha (1)}\cdots s_{\alpha (k)})[B_{\eta }(p_{k+1})]$
is at most
![]() $2\eta (L+\epsilon )/(\lambda ')^k$
, because we have equation (4.15) and each
$2\eta (L+\epsilon )/(\lambda ')^k$
, because we have equation (4.15) and each
![]() $\rho '(s_{\alpha (j)}) (1\le j\le k)$
is
$\rho '(s_{\alpha (j)}) (1\le j\le k)$
is
![]() $(1/\lambda ')$
-contracting on
$(1/\lambda ')$
-contracting on
![]() $\rho '(s_{\alpha (j)}^{-1})[U_{\alpha (j)}\cap K]$
by equation (4.9), and the last map
$\rho '(s_{\alpha (j)}^{-1})[U_{\alpha (j)}\cap K]$
by equation (4.9), and the last map
![]() $\rho '(s_{\alpha (0)})$
is
$\rho '(s_{\alpha (0)})$
is
![]() $(L+\epsilon )$
-Lipschitz on
$(L+\epsilon )$
-Lipschitz on
![]() $B_{\eta }(p_1)\subset N_{\delta }(\Lambda )$
by equation (4.10). Hence, the exponentially shrinking property also holds.
$B_{\eta }(p_1)\subset N_{\delta }(\Lambda )$
by equation (4.10). Hence, the exponentially shrinking property also holds.
If the
![]() $\delta $
-code
$\delta $
-code
![]() $(\alpha ,p)$
is special, then the inclusion equation (4.15) as well as equation (4.16) hold for
$(\alpha ,p)$
is special, then the inclusion equation (4.15) as well as equation (4.16) hold for
![]() $k=0$
. Thus,
$k=0$
. Thus,
for all
![]() $\eta \in [t,\delta ]$
. It follows that
$\eta \in [t,\delta ]$
. It follows that
![]() $d(x,\phi _{\alpha }(x))<t$
.
$d(x,\phi _{\alpha }(x))<t$
.
4.4
 $\phi $
is well-defined
$\phi $
is well-defined
To show that
![]() $\phi $
is well defined, we need to show that
$\phi $
is well defined, we need to show that
![]() $\phi _{\alpha }(x)=\phi _{\beta }(x)$
for any two
$\phi _{\alpha }(x)=\phi _{\beta }(x)$
for any two
![]() $(\mathcal {D}_0,\delta _0)$
-codes
$(\mathcal {D}_0,\delta _0)$
-codes
![]() $(\alpha ,p)$
and
$(\alpha ,p)$
and
![]() $(\beta ,q)$
. Since
$(\beta ,q)$
. Since
![]() $\rho $
is meandering-hyperbolic with the datum
$\rho $
is meandering-hyperbolic with the datum
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
, the corresponding
$(\mathcal {D}_0\prec \mathcal {D};N)$
, the corresponding
![]() $(\mathcal {D}_0,\delta _0)$
-rays
$(\mathcal {D}_0,\delta _0)$
-rays
![]() $c^{\alpha }$
and
$c^{\alpha }$
and
![]() $c^{\beta }$
are
$c^{\beta }$
are
![]() $(\mathcal {D},\delta ;N)$
-equivalent, that is,
$(\mathcal {D},\delta ;N)$
-equivalent, that is,
![]() $c^{\alpha }\sim ^N_{(\mathcal {D},\delta )} c^{\beta }$
in
$c^{\alpha }\sim ^N_{(\mathcal {D},\delta )} c^{\beta }$
in
![]() $\mathrm {Ray}_x(\mathcal {D},\delta )$
. By definition, the equivalence relation
$\mathrm {Ray}_x(\mathcal {D},\delta )$
. By definition, the equivalence relation
![]() $\sim ^N_{(\mathcal {D},\delta )}$
is generated by the relation
$\sim ^N_{(\mathcal {D},\delta )}$
is generated by the relation
![]() $\approx ^N_{(\mathcal {D},\delta )}$
(see Definition 3.23(a)). Thus, it suffices to show the equality
$\approx ^N_{(\mathcal {D},\delta )}$
(see Definition 3.23(a)). Thus, it suffices to show the equality
![]() $\phi _{\alpha }(x)=\phi _{\beta }(x)$
when
$\phi _{\alpha }(x)=\phi _{\beta }(x)$
when
![]() $c^{\alpha }$
and
$c^{\alpha }$
and
![]() $c^{\beta }$
are
$c^{\beta }$
are
![]() $(\mathcal {D},\delta )$
-rays and satisfy
$(\mathcal {D},\delta )$
-rays and satisfy
![]() $c^{\alpha }\approx ^N_{(\mathcal {D},\delta )} c^{\beta }$
, that is, there exist infinite subsets
$c^{\alpha }\approx ^N_{(\mathcal {D},\delta )} c^{\beta }$
, that is, there exist infinite subsets
![]() $P,\,Q\subset \mathbb {N}_0$
such that the subsets
$P,\,Q\subset \mathbb {N}_0$
such that the subsets
![]() $c^{\alpha }(P)$
and
$c^{\alpha }(P)$
and
![]() $c^{\beta }(Q)$
are within Hausdorff distance N from each other in
$c^{\beta }(Q)$
are within Hausdorff distance N from each other in
![]() $(\Gamma ,d_{\varSigma })$
.
$(\Gamma ,d_{\varSigma })$
.
Suppose to the contrary that
Since the open sets
![]() $\rho '(c^{\beta }_j)[B_{\delta }(q_{j+1})]$
shrink to
$\rho '(c^{\beta }_j)[B_{\delta }(q_{j+1})]$
shrink to
![]() $\phi _{\beta }(x)$
, there exists an integer
$\phi _{\beta }(x)$
, there exists an integer
![]() $n\in Q$
such that
$n\in Q$
such that
![]() $\phi _{\alpha }(x)\notin \rho '(c^{\beta }_n)[B_{\delta }(q_{n+1})]$
, that is,
$\phi _{\alpha }(x)\notin \rho '(c^{\beta }_n)[B_{\delta }(q_{n+1})]$
, that is,
Since the Hausdorff distance between
![]() $\{c^{\alpha }_k\}_{k\in P}$
and
$\{c^{\alpha }_k\}_{k\in P}$
and
![]() $\{c^{\beta }_j\}_{j\in Q}$
is at most N, there is an integer
$\{c^{\beta }_j\}_{j\in Q}$
is at most N, there is an integer
![]() $m\in P$
such that
$m\in P$
such that
![]() $d_{\varSigma }(c^{\beta }_n,c^{\alpha }_m)\le N$
. Set
$d_{\varSigma }(c^{\beta }_n,c^{\alpha }_m)\le N$
. Set
so that
![]() $|r|_{\varSigma }\le N$
. Note from Remark 3.13(b) that
$|r|_{\varSigma }\le N$
. Note from Remark 3.13(b) that
![]() $\rho (r)$
maps
$\rho (r)$
maps
![]() $p_{m+1}$
to
$p_{m+1}$
to
![]() $q_{n+1}$
:
$q_{n+1}$
:
See Figure 3.

Figure 3 The points
![]() $\phi _{\alpha }(x)$
and
$\phi _{\alpha }(x)$
and
![]() $\phi _{\beta }(x)$
.
$\phi _{\beta }(x)$
.
In view of Lemma 4.12 (with
![]() $t=\eta =\kappa =\min \{\frac {\delta }{(N+1)L^N},1\}$
), we may assume that we used
$t=\eta =\kappa =\min \{\frac {\delta }{(N+1)L^N},1\}$
), we may assume that we used
![]() $\kappa $
-balls in the definition of
$\kappa $
-balls in the definition of
![]() $\phi _{\alpha }(x)$
so that
$\phi _{\alpha }(x)$
so that
Now, if we show that
![]() $\rho '(r)$
maps
$\rho '(r)$
maps
![]() $B_{\kappa }(p_{m+1})$
into
$B_{\kappa }(p_{m+1})$
into
![]() $B_{\delta }(q_{n+1})$
and hence
$B_{\delta }(q_{n+1})$
and hence
 $$ \begin{align*} \rho'(c^{\beta}_{n})^{-1}(\phi_{\alpha}(x)) &=\rho'(r)[\rho'(c^{\alpha}_{m})^{-1}(\phi_{\alpha}(x))]\\ &\in\rho'(r)[B_{\kappa}(p_{m+1})]\subset B_{\delta}(q_{n+1}), \end{align*} $$
$$ \begin{align*} \rho'(c^{\beta}_{n})^{-1}(\phi_{\alpha}(x)) &=\rho'(r)[\rho'(c^{\alpha}_{m})^{-1}(\phi_{\alpha}(x))]\\ &\in\rho'(r)[B_{\kappa}(p_{m+1})]\subset B_{\delta}(q_{n+1}), \end{align*} $$
then we are done since we are in contradiction with equation (4.17).
To show
![]() $\rho '(r)[B_{\kappa }(p_{m+1})]\subset B_{\delta }(q_{n+1})$
, let
$\rho '(r)[B_{\kappa }(p_{m+1})]\subset B_{\delta }(q_{n+1})$
, let
![]() $l=|r|_{\varSigma }\le N$
. If
$l=|r|_{\varSigma }\le N$
. If
![]() $y\in B_{\kappa }(p_{m+1})\subset N_{\kappa }(\Lambda )$
, then
$y\in B_{\kappa }(p_{m+1})\subset N_{\kappa }(\Lambda )$
, then
 $$ \begin{align*} d(\rho'(r)(y),q_{n+1}) &= d(\rho'(r)(y),\rho(r)(p_{m+1}))\\ &\le d(\rho'(r)(y),\rho(r)(y)) +d(\rho(r)(y),\rho(r)(p_{m+1}))\\ &< k L^{l-1}\epsilon +L^l\kappa\\ &< N L^{N-1}L\kappa +L^N\kappa\le \delta, \end{align*} $$
$$ \begin{align*} d(\rho'(r)(y),q_{n+1}) &= d(\rho'(r)(y),\rho(r)(p_{m+1}))\\ &\le d(\rho'(r)(y),\rho(r)(y)) +d(\rho(r)(y),\rho(r)(p_{m+1}))\\ &< k L^{l-1}\epsilon +L^l\kappa\\ &< N L^{N-1}L\kappa +L^N\kappa\le \delta, \end{align*} $$
where the second inequality holds by Lemma 4.11 and since
![]() $\rho (r)$
is
$\rho (r)$
is
![]() $L^l$
-Lipschitz on
$L^l$
-Lipschitz on
![]() $N_{\delta /L^{l-1}}(\Lambda )\supset B_{\kappa }(p_{m+1})$
by equation (3.5), and the third inequality holds since
$N_{\delta /L^{l-1}}(\Lambda )\supset B_{\kappa }(p_{m+1})$
by equation (3.5), and the third inequality holds since
![]() $\epsilon =\frac {\lambda -1}{2}\kappa <L\kappa $
.
$\epsilon =\frac {\lambda -1}{2}\kappa <L\kappa $
.
This completes the proof of the equality
![]() $\phi _{\alpha }(x)=\phi _{\beta }(x)$
.
$\phi _{\alpha }(x)=\phi _{\beta }(x)$
.
From now on, we may write
![]() $\phi (x)$
for
$\phi (x)$
for
![]() $x\in \Lambda $
without ambiguity. An immediate consequence of this is that we are henceforth free to choose a special
$x\in \Lambda $
without ambiguity. An immediate consequence of this is that we are henceforth free to choose a special
![]() $\delta $
-code for x. Without loss of generality, we may assume that
$\delta $
-code for x. Without loss of generality, we may assume that
![]() $N\geq 4$
. Then from Lemma 4.12 (with
$N\geq 4$
. Then from Lemma 4.12 (with
![]() $t=\kappa =\min \{\frac {\delta }{(N+1)L^N},1\}$
), we conclude that
$t=\kappa =\min \{\frac {\delta }{(N+1)L^N},1\}$
), we conclude that
 $$ \begin{align} d(x,\phi(x))<\kappa\le\frac{\delta}{(N+1)L^N}<\frac{\delta}{5} \end{align} $$
$$ \begin{align} d(x,\phi(x))<\kappa\le\frac{\delta}{(N+1)L^N}<\frac{\delta}{5} \end{align} $$
for all
![]() $x\in \Lambda $
.
$x\in \Lambda $
.
4.5
 $\phi $
is equivariant
$\phi $
is equivariant
To show the equivariance of
![]() $\phi $
, it suffices to check it on the generating set
$\phi $
, it suffices to check it on the generating set
![]() $\varSigma $
of
$\varSigma $
of
![]() $\Gamma $
.
$\Gamma $
.
Given
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $s\in \varSigma $
, set
$s\in \varSigma $
, set
![]() $y=\rho (s^{-1})(x)$
. Let
$y=\rho (s^{-1})(x)$
. Let
![]() $(\beta ,q)$
be a special
$(\beta ,q)$
be a special
![]() $\delta $
-code for y so that
$\delta $
-code for y so that
![]() $B_{\delta }(y)\subset U_{\beta (0)}$
(see Definition 3.10). Then we consider a
$B_{\delta }(y)\subset U_{\beta (0)}$
(see Definition 3.10). Then we consider a
![]() $\delta $
-code
$\delta $
-code
![]() $(\alpha ,p)$
for x defined by
$(\alpha ,p)$
for x defined by
![]() $s_{\alpha (0)}=s$
and
$s_{\alpha (0)}=s$
and
 $$ \begin{align*} {\alpha(k)}&={\beta(k-1)},\\ p_k&=q_{k-1} \end{align*} $$
$$ \begin{align*} {\alpha(k)}&={\beta(k-1)},\\ p_k&=q_{k-1} \end{align*} $$
for
![]() $k\in \mathbb {N}$
: Indeed, we verify the requirement that
$k\in \mathbb {N}$
: Indeed, we verify the requirement that
for
![]() $k\in \mathbb {N}$
. The associated rays
$k\in \mathbb {N}$
. The associated rays
![]() $\{c^{\alpha }_k\}_{k\in \mathbb {N}_0}$
and
$\{c^{\alpha }_k\}_{k\in \mathbb {N}_0}$
and
![]() $\{c^{\beta }_k\}_{k\in \mathbb {N}_0}$
(see Definition 3.12) are related by
$\{c^{\beta }_k\}_{k\in \mathbb {N}_0}$
(see Definition 3.12) are related by
for
![]() $k\in \mathbb {N}$
. Therefore, we have
$k\in \mathbb {N}$
. Therefore, we have
 $$ \begin{align*} \{\phi[\rho(s)(y)]\}=\{\phi(x)\} &=\bigcap_{k=0}^{\infty} \rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})] \\ &=\bigcap_{k=1}^{\infty} \rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})] \\ &=\bigcap_{k=1}^{\infty} \rho'(s)\rho'(c^{\beta}_{k-1})[B_{\delta}(q_k)] \\ &=\rho'(s)\left[\bigcap_{k=0}^{\infty} \rho'(c^{\beta}_{k})[B_{\delta}(q_{k+1})] \right] =\rho'(s)\{\phi(y)\}, \end{align*} $$
$$ \begin{align*} \{\phi[\rho(s)(y)]\}=\{\phi(x)\} &=\bigcap_{k=0}^{\infty} \rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})] \\ &=\bigcap_{k=1}^{\infty} \rho'(c^{\alpha}_k)[B_{\delta}(p_{k+1})] \\ &=\bigcap_{k=1}^{\infty} \rho'(s)\rho'(c^{\beta}_{k-1})[B_{\delta}(q_k)] \\ &=\rho'(s)\left[\bigcap_{k=0}^{\infty} \rho'(c^{\beta}_{k})[B_{\delta}(q_{k+1})] \right] =\rho'(s)\{\phi(y)\}, \end{align*} $$
which implies the equivariance of
![]() $\phi $
.
$\phi $
.
4.6
 $\phi $
is continuous
$\phi $
is continuous
Let
![]() $\zeta>0$
be given. In order to show that
$\zeta>0$
be given. In order to show that
![]() $\phi $
is continuous at
$\phi $
is continuous at
![]() $x\in \Lambda $
, assign a
$x\in \Lambda $
, assign a
![]() $(\mathcal {D},\delta )$
-code
$(\mathcal {D},\delta )$
-code
![]() $(\alpha ,p)$
for x which comes from a
$(\alpha ,p)$
for x which comes from a
![]() $(\mathcal {D},\delta _0)$
-code for x. (Recall
$(\mathcal {D},\delta _0)$
-code for x. (Recall
![]() $\delta _0>\delta $
and Remark 3.11(c). Also note that Lemma 4.12 applies to the
$\delta _0>\delta $
and Remark 3.11(c). Also note that Lemma 4.12 applies to the
![]() $(\mathcal {D},\delta )$
-code
$(\mathcal {D},\delta )$
-code
![]() $(\alpha ,p)$
with
$(\alpha ,p)$
with
![]() $\eta =\delta $
). Choose an integer
$\eta =\delta $
). Choose an integer
![]() $j\in \mathbb {N}_0$
such that
$j\in \mathbb {N}_0$
such that
![]() $2\delta _0(L+\epsilon )/(\lambda ')^{j}<\zeta $
, where the constants
$2\delta _0(L+\epsilon )/(\lambda ')^{j}<\zeta $
, where the constants
![]() $\lambda '$
and
$\lambda '$
and
![]() $\epsilon $
are from Section 4.2. Since
$\epsilon $
are from Section 4.2. Since
![]() $\rho (c^{\alpha }_j)^{-1}$
maps x to
$\rho (c^{\alpha }_j)^{-1}$
maps x to
![]() $p_{j+1}$
and is continuous, there exists
$p_{j+1}$
and is continuous, there exists
![]() $\zeta '>0$
such that
$\zeta '>0$
such that
![]() $\rho (c^{\alpha }_j)^{-1}[B_{\zeta '}(x)]\subset B_{\delta _0-\delta }(p_{j+1})$
. Below we will show that, if
$\rho (c^{\alpha }_j)^{-1}[B_{\zeta '}(x)]\subset B_{\delta _0-\delta }(p_{j+1})$
. Below we will show that, if
![]() $y\in \Lambda $
satisfies
$y\in \Lambda $
satisfies
![]() $d(x,y)<\zeta '$
, then
$d(x,y)<\zeta '$
, then
![]() $d(\phi (x),\phi (y))<\zeta $
thereby proving that
$d(\phi (x),\phi (y))<\zeta $
thereby proving that
![]() $\phi $
is continuous at x.
$\phi $
is continuous at x.
Let
![]() $y\in \Lambda $
be such that
$y\in \Lambda $
be such that
![]() $d(x,y)<\zeta '$
. Then
$d(x,y)<\zeta '$
. Then
![]() $\rho (c^{\alpha }_j)^{-1}(y)\in B_{\delta _0-\delta }(p_{j+1})$
, hence
$\rho (c^{\alpha }_j)^{-1}(y)\in B_{\delta _0-\delta }(p_{j+1})$
, hence
by Lemma 3.14(i). In other words, for
![]() $0\leq k\leq j$
, we have
$0\leq k\leq j$
, we have
 $$ \begin{align*} \rho(c^{\alpha}_k)^{-1}(y) &\in B_{\delta_0-\delta}(p_{k+1}), \\ \mathrm{hence}\quad B_{\delta}(\rho(c^{\alpha}_k)^{-1}(y)) &\subset B_{\delta_0}(p_{k+1}) \subset U_{\alpha(k+1)}. \end{align*} $$
$$ \begin{align*} \rho(c^{\alpha}_k)^{-1}(y) &\in B_{\delta_0-\delta}(p_{k+1}), \\ \mathrm{hence}\quad B_{\delta}(\rho(c^{\alpha}_k)^{-1}(y)) &\subset B_{\delta_0}(p_{k+1}) \subset U_{\alpha(k+1)}. \end{align*} $$
This means that there is a
![]() $\delta $
-code
$\delta $
-code
![]() $(\beta ,q)$
for
$(\beta ,q)$
for
![]() $y\in \Lambda $
with a property that
$y\in \Lambda $
with a property that
In particular,
![]() $c^{\beta }_j=c^{\alpha }_j$
and hence
$c^{\beta }_j=c^{\alpha }_j$
and hence
![]() $q_{j+1}=\rho (c^{\beta }_j)^{-1}(y)=\rho (c^{\alpha }_j)^{-1}(y)\in B_{\delta _0-\delta }(p_{j+1})$
. Consequently, we have
$q_{j+1}=\rho (c^{\beta }_j)^{-1}(y)=\rho (c^{\alpha }_j)^{-1}(y)\in B_{\delta _0-\delta }(p_{j+1})$
. Consequently, we have
![]() $B_{\delta }(q_{j+1})\subset B_{\delta _0}(p_{j+1})$
and
$B_{\delta }(q_{j+1})\subset B_{\delta _0}(p_{j+1})$
and
 $$ \begin{align*} \{\phi(y)\} &=\bigcap_{k=0}^{\infty} \rho'(c^{\beta}_k)[B_{\delta}(q_{k+1})]\\ &\subset \rho'(c^{\beta}_j)[B_{\delta}(q_{j+1})]\\ &=\rho'(c^{\alpha}_j)[B_{\delta}(q_{j+1})]\\ &\subset\rho'(c^{\alpha}_j)[B_{\delta_0}(p_{j+1})]. \end{align*} $$
$$ \begin{align*} \{\phi(y)\} &=\bigcap_{k=0}^{\infty} \rho'(c^{\beta}_k)[B_{\delta}(q_{k+1})]\\ &\subset \rho'(c^{\beta}_j)[B_{\delta}(q_{j+1})]\\ &=\rho'(c^{\alpha}_j)[B_{\delta}(q_{j+1})]\\ &\subset\rho'(c^{\alpha}_j)[B_{\delta_0}(p_{j+1})]. \end{align*} $$
By (the proof of) Lemma 4.12, the diameter of the last set
![]() $\rho '(c^{\alpha }_j)[B_{\delta _0}(p_{j+1})]$
is at most
$\rho '(c^{\alpha }_j)[B_{\delta _0}(p_{j+1})]$
is at most
![]() $2{\delta _0}(L+\epsilon )/(\lambda ')^{j}<\zeta $
. Since
$2{\delta _0}(L+\epsilon )/(\lambda ')^{j}<\zeta $
. Since
![]() $\phi (x)\in \rho '(c^{\alpha }_j)[B_{\delta _0}(p_{j+1})]$
as well, we showed
$\phi (x)\in \rho '(c^{\alpha }_j)[B_{\delta _0}(p_{j+1})]$
as well, we showed
as desired.
4.7
 $\phi $
is injective
$\phi $
is injective
Suppose, to the contrary, that
![]() $\phi (x)=\phi (y)$
but
$\phi (x)=\phi (y)$
but
![]() $x\neq y$
. Since
$x\neq y$
. Since
![]() $\phi $
is equivariant, we then have
$\phi $
is equivariant, we then have
![]() $\phi [\rho (g)(x)]=\phi [\rho (g)(y)]$
for any
$\phi [\rho (g)(x)]=\phi [\rho (g)(y)]$
for any
![]() $g\in \Gamma $
, hence, by equation (4.18),
$g\in \Gamma $
, hence, by equation (4.18),
for all
![]() $g\in \Gamma $
. But this contradicts Corollary 3.19 since
$g\in \Gamma $
. But this contradicts Corollary 3.19 since
![]() $\rho $
has an expansivity constant
$\rho $
has an expansivity constant
![]() $2\delta /5$
. Therefore,
$2\delta /5$
. Therefore,
![]() $\phi $
is injective.
$\phi $
is injective.
So far, we have proved the claim that
![]() $\phi $
is an equivariant homeomorphism. This completes the proof of Theorem 4.4(1).
$\phi $
is an equivariant homeomorphism. This completes the proof of Theorem 4.4(1).
4.8
 $\phi $
depends continuously on
$\phi $
depends continuously on
 $\rho '$
$\rho '$
We show that the map
 $$ \begin{align*} \mathrm{Hom}(\Gamma,\mathrm{LHomeo}(M)) \supset U(\rho;K,\epsilon)&\to C^0(\Lambda,(M,d))\\ \rho'&\mapsto \phi \end{align*} $$
$$ \begin{align*} \mathrm{Hom}(\Gamma,\mathrm{LHomeo}(M)) \supset U(\rho;K,\epsilon)&\to C^0(\Lambda,(M,d))\\ \rho'&\mapsto \phi \end{align*} $$
is continuous at
![]() $\rho $
, where we equip
$\rho $
, where we equip
![]() $\mathrm {Hom}(\Gamma , \mathrm {LHomeo}(M))$
with the topology of ‘algebraic convergence’ as in Section 4.1 and
$\mathrm {Hom}(\Gamma , \mathrm {LHomeo}(M))$
with the topology of ‘algebraic convergence’ as in Section 4.1 and
![]() $C^0(\Lambda ,(M,d))$
with the uniform topology. This will imply that, if
$C^0(\Lambda ,(M,d))$
with the uniform topology. This will imply that, if
![]() $\rho '$
is close to
$\rho '$
is close to
![]() $\rho $
, then
$\rho $
, then
![]() $\phi $
is close to the identity map and, as for
$\phi $
is close to the identity map and, as for
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '=\phi (\Lambda )$
, that the map
$\Lambda '=\phi (\Lambda )$
, that the map
![]() $\rho '\mapsto d_{\mathrm {Haus}}(\Lambda ,\Lambda ')$
is continuous at
$\rho '\mapsto d_{\mathrm {Haus}}(\Lambda ,\Lambda ')$
is continuous at
![]() $\rho $
, where
$\rho $
, where
![]() $d_{\mathrm {Haus}}$
stands for the Hausdorff distance.
$d_{\mathrm {Haus}}$
stands for the Hausdorff distance.
To prove the claim, suppose a sufficiently small constant
![]() $t>0$
is given. Of course, we may assume
$t>0$
is given. Of course, we may assume
![]() $t\le \min \{\frac {\delta }{(N+1)L^N},1\}$
. Then we have to find a neighborhood
$t\le \min \{\frac {\delta }{(N+1)L^N},1\}$
. Then we have to find a neighborhood
![]() $U(\rho ;K',\epsilon ')$
of
$U(\rho ;K',\epsilon ')$
of
![]() $\rho $
such that
$\rho $
such that
![]() $\sup \{d(x,\phi (x))\mid x\in \Lambda \}<t$
for every
$\sup \{d(x,\phi (x))\mid x\in \Lambda \}<t$
for every
![]() $\rho '\in U(\rho ;K',\epsilon ')$
. So, we let
$\rho '\in U(\rho ;K',\epsilon ')$
. So, we let
Suppose
![]() $\rho '\in U(\rho ;K',\epsilon ')$
. Let
$\rho '\in U(\rho ;K',\epsilon ')$
. Let
![]() $x\in \Lambda $
, and choose a special
$x\in \Lambda $
, and choose a special
![]() $\delta $
-code
$\delta $
-code
![]() $(\alpha ,p)$
for x. Then by Lemma 4.12, we have
$(\alpha ,p)$
for x. Then by Lemma 4.12, we have
![]() $d(x,\phi (x))=d(x,\phi _{\alpha }(x))<t$
. Since
$d(x,\phi (x))=d(x,\phi _{\alpha }(x))<t$
. Since
![]() $x\in \Lambda $
is arbitrary, the proof is complete.
$x\in \Lambda $
is arbitrary, the proof is complete.
4.9
 $\rho '$
is expanding
$\rho '$
is expanding
We now show how, given an expansion datum
![]() $\mathcal {D}$
of the action
$\mathcal {D}$
of the action
![]() $\rho $
, to get a new expansion datum
$\rho $
, to get a new expansion datum
![]() $\mathcal {D}'=(\mathcal {I}',\mathcal {U}',\varSigma ', \delta ',L',\lambda ')$
of the action
$\mathcal {D}'=(\mathcal {I}',\mathcal {U}',\varSigma ', \delta ',L',\lambda ')$
of the action
![]() $\rho '$
.
$\rho '$
.
First, take the same data
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\varSigma $
of
$\varSigma $
of
![]() $\mathcal {D}$
that is, set
$\mathcal {D}$
that is, set
![]() $\mathcal {I}'=\mathcal {I}$
and
$\mathcal {I}'=\mathcal {I}$
and
![]() $\varSigma '=\varSigma $
, and set
$\varSigma '=\varSigma $
, and set
![]() $L'=L+\epsilon $
and
$L'=L+\epsilon $
and
![]() $\lambda '=\lambda -\epsilon $
from equations (4.10) and (4.9). Then every
$\lambda '=\lambda -\epsilon $
from equations (4.10) and (4.9). Then every
![]() $\rho '(s_i^{-1})$
is
$\rho '(s_i^{-1})$
is
![]() $\lambda '$
-expanding on
$\lambda '$
-expanding on
![]() $U_i\cap N_{\delta }(\Lambda )$
and
$U_i\cap N_{\delta }(\Lambda )$
and
![]() $L'$
-Lipschitz on
$L'$
-Lipschitz on
![]() $N_{\delta }(\Lambda )$
. For a positive number
$N_{\delta }(\Lambda )$
. For a positive number
![]() $r<4\delta /5$
, if we set
$r<4\delta /5$
, if we set
(recall equation (2.1) for the definition of
![]() $U^{r}$
), then by Remark 3.6(e) there is a constant
$U^{r}$
), then by Remark 3.6(e) there is a constant
![]() $\delta '=\delta '(r)>0$
such that every
$\delta '=\delta '(r)>0$
such that every
![]() $\rho '(s_i^{-1})$
is
$\rho '(s_i^{-1})$
is
![]() $(\lambda ',U_{\alpha }';\delta ')$
-expanding. Note that
$(\lambda ',U_{\alpha }';\delta ')$
-expanding. Note that
![]() $\delta '$
can be chosen as small as we want, and thus we may assume that
$\delta '$
can be chosen as small as we want, and thus we may assume that
![]() $\delta '<4\delta /5$
. Let
$\delta '<4\delta /5$
. Let
![]() $x\in \Lambda $
. Then, since
$x\in \Lambda $
. Then, since
![]() $d(x,\phi (x))<\delta /5$
by equation (4.18) and
$d(x,\phi (x))<\delta /5$
by equation (4.18) and
![]() $0<r<4\delta /5$
, it follows that
$0<r<4\delta /5$
, it follows that
for some
![]() $i\in \mathcal {I}$
, and hence
$i\in \mathcal {I}$
, and hence
![]() $\phi (x)\in U^{\prime }_i$
. This implies that
$\phi (x)\in U^{\prime }_i$
. This implies that
![]() $\mathcal {U}'$
covers
$\mathcal {U}'$
covers
![]() $\Lambda '$
and
$\Lambda '$
and
![]() $N_{\delta '}(\Lambda ')\subset N_{\delta }(\Lambda )$
. Thus, every
$N_{\delta '}(\Lambda ')\subset N_{\delta }(\Lambda )$
. Thus, every
![]() $\rho '(s_i^{-1})$
is
$\rho '(s_i^{-1})$
is
![]() $L'$
-Lipschitz on
$L'$
-Lipschitz on
![]() $N_{\delta '}(\Lambda ')$
. If we choose
$N_{\delta '}(\Lambda ')$
. If we choose
![]() $\delta '$
so that
$\delta '$
so that
![]() $\delta '$
is smaller than a Lebesgue number of the open covering
$\delta '$
is smaller than a Lebesgue number of the open covering
![]() $\mathcal {U}'$
of
$\mathcal {U}'$
of
![]() $\Lambda '$
, the properties (i) and (ii) of Definition 3.4 are verified for
$\Lambda '$
, the properties (i) and (ii) of Definition 3.4 are verified for
![]() $\rho '$
with the datum
$\rho '$
with the datum
![]() $\mathcal {D}'=(\mathcal {I}',\mathcal {U}',\varSigma ', \delta ',L',\lambda ')$
. Therefore,
$\mathcal {D}'=(\mathcal {I}',\mathcal {U}',\varSigma ', \delta ',L',\lambda ')$
. Therefore,
![]() $\rho '$
is expanding.
$\rho '$
is expanding.
4.10
 $\rho '$
is again uniformly meandering-hyperbolic
$\rho '$
is again uniformly meandering-hyperbolic
Assume that the action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is uniformly meandering-hyperbolic with a datum
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is uniformly meandering-hyperbolic with a datum
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
(Definition 3.26). Then, for every
$(\mathcal {D}_0\prec \mathcal {D};N)$
(Definition 3.26). Then, for every
![]() $\eta \in (0,\delta ]$
and every
$\eta \in (0,\delta ]$
and every
![]() $x\in \Lambda $
, all rays in
$x\in \Lambda $
, all rays in
![]() $\mathrm {Ray}_x(\mathcal {D}_0,\eta )$
are
$\mathrm {Ray}_x(\mathcal {D}_0,\eta )$
are
![]() $(\mathcal {D},\eta ;N)$
-equivalent. In order to show that every
$(\mathcal {D},\eta ;N)$
-equivalent. In order to show that every
![]() $\rho '\in U(\rho ;K,\epsilon )$
is uniformly meandering-hyperbolic, we first let
$\rho '\in U(\rho ;K,\epsilon )$
is uniformly meandering-hyperbolic, we first let
![]() $\mathcal {D}'$
be the expansion data of
$\mathcal {D}'$
be the expansion data of
![]() $\rho '$
obtained from
$\rho '$
obtained from
![]() $\mathcal {D}$
via the way described in Section 4.9 by taking
$\mathcal {D}$
via the way described in Section 4.9 by taking
![]() $r=\delta /5$
so that, in particular,
$r=\delta /5$
so that, in particular,
Then, we will define an expansion data
![]() $\mathcal {D}_0'\prec \mathcal {D}'$
of
$\mathcal {D}_0'\prec \mathcal {D}'$
of
![]() $\rho '$
and show that
$\rho '$
and show that
![]() $(\mathcal {D}_0'\prec \mathcal {D}';N)$
is a uniform meandering hyperbolicity datum of
$(\mathcal {D}_0'\prec \mathcal {D}';N)$
is a uniform meandering hyperbolicity datum of
![]() $\rho '$
.
$\rho '$
.
Since
![]() $\mathcal {D}_0\prec D$
, one can easily derive an expansion datum
$\mathcal {D}_0\prec D$
, one can easily derive an expansion datum
![]() $\mathcal {D}_0'=(\mathcal {I}^{\prime }_0,\mathcal {U}^{\prime }_0,\varSigma ^{\prime }_0, \delta ^{\prime }_0,L^{\prime }_0,\lambda ^{\prime }_0)$
of
$\mathcal {D}_0'=(\mathcal {I}^{\prime }_0,\mathcal {U}^{\prime }_0,\varSigma ^{\prime }_0, \delta ^{\prime }_0,L^{\prime }_0,\lambda ^{\prime }_0)$
of
![]() $\rho '$
from
$\rho '$
from
![]() $\mathcal {D}_0$
as follows. Set
$\mathcal {D}_0$
as follows. Set
![]() $\mathcal {I}_0'=\mathcal {I}_0$
,
$\mathcal {I}_0'=\mathcal {I}_0$
,
![]() $\varSigma ^{\prime }_0=\varSigma _0$
,
$\varSigma ^{\prime }_0=\varSigma _0$
,
![]() $L^{\prime }_0=L'$
and
$L^{\prime }_0=L'$
and
![]() $\lambda ^{\prime }_0=\lambda '$
. Let
$\lambda ^{\prime }_0=\lambda '$
. Let
![]() $\mathcal {U}_0=\{U_{0,i} \mid i\in \mathcal {I}_0\}$
. From
$\mathcal {U}_0=\{U_{0,i} \mid i\in \mathcal {I}_0\}$
. From
![]() $\mathcal {U}_0\prec \mathcal {U}$
, it immediately follows that
$\mathcal {U}_0\prec \mathcal {U}$
, it immediately follows that
![]() $\rho '(s_i^{-1})$
is
$\rho '(s_i^{-1})$
is
![]() $\lambda '$
-expanding on
$\lambda '$
-expanding on
![]() $U_{0,i}\cap N_{\delta }(\Lambda )$
and
$U_{0,i}\cap N_{\delta }(\Lambda )$
and
![]() $L'$
-Lipschitz on
$L'$
-Lipschitz on
![]() $N_{\delta }(\Lambda )$
for all
$N_{\delta }(\Lambda )$
for all
![]() $i \in \mathcal {I}_0$
. If we set
$i \in \mathcal {I}_0$
. If we set
then Remark 3.6(e) implies that there is
![]() $\delta _0'>0$
such that
$\delta _0'>0$
such that
![]() $\rho '(s_i^{-1})$
is
$\rho '(s_i^{-1})$
is
![]() $(\lambda ',U_{0,i}';\delta _0')$
-expanding for all
$(\lambda ',U_{0,i}';\delta _0')$
-expanding for all
![]() $i\in \mathcal {I}_0$
. For any
$i\in \mathcal {I}_0$
. For any
![]() $x\in \Lambda $
, since
$x\in \Lambda $
, since
![]() $d(x,\phi (x))<\delta /5$
, we have
$d(x,\phi (x))<\delta /5$
, we have
for some
![]() $i\in \mathcal {I}_0$
. We may choose
$i\in \mathcal {I}_0$
. We may choose
![]() $\delta _0'$
and
$\delta _0'$
and
![]() $\delta '$
so that
$\delta '$
so that
![]() $\delta '<\delta _0'<2\delta /5$
. Then
$\delta '<\delta _0'<2\delta /5$
. Then
![]() $\mathcal {D}_0'$
is another expansion datum of
$\mathcal {D}_0'$
is another expansion datum of
![]() $\rho '$
such that
$\rho '$
such that
![]() $\mathcal {D}_0'\prec \mathcal {D}'$
.
$\mathcal {D}_0'\prec \mathcal {D}'$
.
In order to check that
![]() $(\mathcal {D}_0'\prec \mathcal {D}';N)$
is a uniform meandering hyperbolicity datum of
$(\mathcal {D}_0'\prec \mathcal {D}';N)$
is a uniform meandering hyperbolicity datum of
![]() $\rho '$
, let
$\rho '$
, let
![]() $0<\eta \leq \delta '<2\delta /5$
and
$0<\eta \leq \delta '<2\delta /5$
and
![]() $x\in \Lambda $
. We need to show that all rays in
$x\in \Lambda $
. We need to show that all rays in
![]() $\mathrm {Ray}_x(\mathcal {D}_0',\eta )$
are
$\mathrm {Ray}_x(\mathcal {D}_0',\eta )$
are
![]() $(\mathcal {D}',\eta ;N)$
-equivalent.
$(\mathcal {D}',\eta ;N)$
-equivalent.
Let
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $(\alpha ,p')$
be a
$(\alpha ,p')$
be a
![]() $(\mathcal {D}_0',\eta )$
-code for
$(\mathcal {D}_0',\eta )$
-code for
![]() $\phi (x)$
. Recall Definition 3.10. Since
$\phi (x)$
. Recall Definition 3.10. Since
![]() $(\alpha ,p')$
is an
$(\alpha ,p')$
is an
![]() $(\mathcal {D}^{\prime }_0,\eta )$
-code for
$(\mathcal {D}^{\prime }_0,\eta )$
-code for
![]() $\phi (x)\in \Lambda '$
, we have
$\phi (x)\in \Lambda '$
, we have
 $$ \begin{align*} p^{\prime}_0&=\phi(x),\\ p^{\prime}_{k+1}&=\rho'(s_{\alpha(k)}^{-1})(p^{\prime}_k),\\ B_{\eta}(p^{\prime}_k)&\subset U^{\prime}_{0,\alpha(k)} \end{align*} $$
$$ \begin{align*} p^{\prime}_0&=\phi(x),\\ p^{\prime}_{k+1}&=\rho'(s_{\alpha(k)}^{-1})(p^{\prime}_k),\\ B_{\eta}(p^{\prime}_k)&\subset U^{\prime}_{0,\alpha(k)} \end{align*} $$
for all
![]() $k\in \mathbb {N}_0$
. By the definition of
$k\in \mathbb {N}_0$
. By the definition of
![]() $U_{0,i}':=\mathrm {int}\, U_{0,i}^{3\delta /5}\cap N_{2\delta /5}(\Lambda )$
, it follows that
$U_{0,i}':=\mathrm {int}\, U_{0,i}^{3\delta /5}\cap N_{2\delta /5}(\Lambda )$
, it follows that
![]() $B_{\eta +3\delta /5}(p_k')\subset U_{0,\alpha (k)}$
for all
$B_{\eta +3\delta /5}(p_k')\subset U_{0,\alpha (k)}$
for all
![]() $k\in \mathbb {N}_0$
. Let
$k\in \mathbb {N}_0$
. Let
![]() $p_k=\phi ^{-1}(p_k')$
for
$p_k=\phi ^{-1}(p_k')$
for
![]() $k\in \mathbb {N}_0$
and
$k\in \mathbb {N}_0$
and
![]() $p : \mathbb {N}_0 \to \Lambda $
be the sequence corresponding to
$p : \mathbb {N}_0 \to \Lambda $
be the sequence corresponding to
![]() $\{p_k\}_{k\in \mathbb {N}_0}$
. We first check
$\{p_k\}_{k\in \mathbb {N}_0}$
. We first check
and then, for
![]() $k\in \mathbb {N}$
, check
$k\in \mathbb {N}$
, check
where the second equality is due to the equivariance of
![]() $\phi $
. Since
$\phi $
. Since
![]() $d(p_k,p_k')<\delta /5$
, we have that for all
$d(p_k,p_k')<\delta /5$
, we have that for all
![]() $k\in \mathbb {N}_0$
,
$k\in \mathbb {N}_0$
,
which implies that
![]() $(\alpha , p)$
is a
$(\alpha , p)$
is a
![]() $(\mathcal {D}_0,\eta +2\delta /5)$
-code for
$(\mathcal {D}_0,\eta +2\delta /5)$
-code for
![]() $x\in \Lambda $
.
$x\in \Lambda $
.
By the uniform meandering hyperbolicity of
![]() $\rho $
, there is a finite chain of interpolating rays
$\rho $
, there is a finite chain of interpolating rays
![]() $c^{\alpha }=c^{\gamma _1}, c^{\gamma _2},\ldots , c^{\gamma _n}=c^{\beta }$
in
$c^{\alpha }=c^{\gamma _1}, c^{\gamma _2},\ldots , c^{\gamma _n}=c^{\beta }$
in
![]() $\mathrm {Ray}_x(\mathcal {D},\eta +2\delta /5)$
such that
$\mathrm {Ray}_x(\mathcal {D},\eta +2\delta /5)$
such that
Claim.
![]() $\mathrm {Ray}_x(\mathcal {D},\eta +2\delta /5)\subset \mathrm {Ray}_{\phi (x)}(\mathcal {D}', \eta )$
.
$\mathrm {Ray}_x(\mathcal {D},\eta +2\delta /5)\subset \mathrm {Ray}_{\phi (x)}(\mathcal {D}', \eta )$
.
If the claim holds, we have
![]() $ c^{\gamma _1} \approx ^N_{(\mathcal {D}',\eta )} c^{\gamma _2} \approx ^N_{(\mathcal {D}',\eta )} \cdots \approx ^N_{(\mathcal {D}',\eta )} c^{\gamma _n}$
and, therefore, we conclude that
$ c^{\gamma _1} \approx ^N_{(\mathcal {D}',\eta )} c^{\gamma _2} \approx ^N_{(\mathcal {D}',\eta )} \cdots \approx ^N_{(\mathcal {D}',\eta )} c^{\gamma _n}$
and, therefore, we conclude that
![]() $\rho '$
is uniformly meandering-hyperbolic with a datum
$\rho '$
is uniformly meandering-hyperbolic with a datum
![]() $(\mathcal {D}_0'\prec \mathcal {D}';N)$
.
$(\mathcal {D}_0'\prec \mathcal {D}';N)$
.
Now, it only remains to prove the claim. Let
![]() $(\gamma , q)$
be a
$(\gamma , q)$
be a
![]() $(\mathcal {D},\eta +2\delta /5)$
-code for
$(\mathcal {D},\eta +2\delta /5)$
-code for
![]() $x\in \Lambda $
. Then for all
$x\in \Lambda $
. Then for all
![]() $k\in \mathbb {N}_0$
,
$k\in \mathbb {N}_0$
,
which implies that
![]() $B_{\eta }(\phi (q_k))\subset U_{\gamma (k)}'$
and thus
$B_{\eta }(\phi (q_k))\subset U_{\gamma (k)}'$
and thus
![]() $(\gamma , q')$
is a
$(\gamma , q')$
is a
![]() $(\mathcal {D}',\eta )$
-code for
$(\mathcal {D}',\eta )$
-code for
![]() $\phi (x)$
as desired, where
$\phi (x)$
as desired, where
![]() $q'$
is the sequence defined by
$q'$
is the sequence defined by
![]() $q^{\prime }_k=\phi (q_k)$
for
$q^{\prime }_k=\phi (q_k)$
for
![]() $k\in \mathbb {N}_0$
. The claim is proved.
$k\in \mathbb {N}_0$
. The claim is proved.
5 Uniform lattices in semisimple Lie groups are structurally stable
In this section, we shall prove the following theorem that, for every uniform lattice
![]() $\Gamma $
in a semisimple Lie group G, the
$\Gamma $
in a semisimple Lie group G, the
![]() $\Gamma $
-action on each flag manifold
$\Gamma $
-action on each flag manifold
![]() $G/P$
is meandering-hyperbolic.
$G/P$
is meandering-hyperbolic.
Theorem 5.1. Let
![]() $\Gamma < G$
be a uniform lattice in a semisimple Lie group G (with finitely many connected components and finite center). Then, for each face
$\Gamma < G$
be a uniform lattice in a semisimple Lie group G (with finitely many connected components and finite center). Then, for each face
![]() ${\tau _{\mathrm {mod}}}\subset {\sigma _{\mathrm {mod}}}$
, the
${\tau _{\mathrm {mod}}}\subset {\sigma _{\mathrm {mod}}}$
, the
![]() $\Gamma $
-action on the flag manifold
$\Gamma $
-action on the flag manifold
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is uniformly meandering-hyperbolic.
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is uniformly meandering-hyperbolic.
From the structural stability theorem (Theorem 4.4), we then conclude:
Corollary 5.2. The actions on flag manifolds of uniform lattices in semisimple Lie groups are structurally stable in the sense of Lipschitz dynamics.
5.1 Sketch of proof
Let X be the symmetric space associated with the semisimple Lie group G. Our proof will use definitions and results regarding asymptotic geometry of X established in a series of papers of Kapovich, Leeb and Porti [Reference Kapovich and Leeb23, Reference Kapovich, Leeb and Porti26, Reference Kapovich, Leeb and Porti27], to which we refer the reader for details; surveys of these notions and results can be found in [Reference Kapovich, Leeb and Porti25, Reference Kapovich and Leeb22].
The key notion used in the proof is the one of Morse quasi-geodesics in X, which was first introduced in [Reference Kapovich, Leeb and Porti24] in order to give one of many alternative interpretations of Anosov subgroups. While uniform lattices in higher rank Lie groups are clearly non-Anosov, some key geometric results developed for the purpose of analyzing Anosov subgroups are still very useful when dealing with higher rank lattices, as we will see below.
In the remainder of the section, we prove Theorem 5.1 in the following steps:
-
(§5.2) we find an expansion datum
 $\mathcal {D}$
for the action;
$\mathcal {D}$
for the action; -
(§5.3) we show that coding rays are Morse quasi-geodesics, and
-
(§5.4) that asymptotic Morse quasi-geodesics can be interpolated;
-
(§5.5) for each
 $\eta \in (0,\delta ]$
, we find a refinement
$\eta \in (0,\delta ]$
, we find a refinement
 $\mathcal {D}_{\eta }$
of the expansion datum
$\mathcal {D}_{\eta }$
of the expansion datum
 $\mathcal {D}$
;
$\mathcal {D}$
; -
(§5.6) we verify the uniform meandering hyperbolicity by using Proposition 5.3 below.
Proposition 5.3. Let
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
be expanding at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
. Suppose that, for each
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
. Suppose that, for each
![]() $\eta \in (0,\delta ]$
, there exist a positive constant
$\eta \in (0,\delta ]$
, there exist a positive constant
![]() $r_{\eta }<\eta $
, an integer
$r_{\eta }<\eta $
, an integer
![]() $N_{\eta }>0$
and an expansion datum
$N_{\eta }>0$
and an expansion datum
![]() $\mathcal {D}_{\eta }=(\mathcal {I}_{\eta },\mathcal {U}_{\eta },\varSigma _{\eta }, r_{\eta },L_{\eta },\lambda _{\eta })\succ \mathcal {D}$
such that, for every
$\mathcal {D}_{\eta }=(\mathcal {I}_{\eta },\mathcal {U}_{\eta },\varSigma _{\eta }, r_{\eta },L_{\eta },\lambda _{\eta })\succ \mathcal {D}$
such that, for every
![]() $x\in \Lambda $
, all rays in
$x\in \Lambda $
, all rays in
![]() $\mathrm {Ray}_x(\mathcal {D},\eta )$
are
$\mathrm {Ray}_x(\mathcal {D},\eta )$
are
![]() $(\mathcal {D}_{\eta },r_{\eta };N_{\eta })$
-equivalent as rays in
$(\mathcal {D}_{\eta },r_{\eta };N_{\eta })$
-equivalent as rays in
![]() $\mathrm {Ray}_x(\mathcal {D}_{\eta },r_{\eta })$
. Then
$\mathrm {Ray}_x(\mathcal {D}_{\eta },r_{\eta })$
. Then
![]() $\rho $
is uniformly meandering-hyperbolic.
$\rho $
is uniformly meandering-hyperbolic.
Proof. To define a uniform meandering hyperbolicity datum of
![]() $\rho $
, we set
$\rho $
, we set
![]() $\delta _0=r_{\delta /2}+\delta /2<\delta $
,
$\delta _0=r_{\delta /2}+\delta /2<\delta $
,
![]() $\mathcal {U}_0=\{\mathrm {int}\, U_{i}^{\delta /2} \mid i\in \mathcal {I}\}$
(recall equation (2.1)) and
$\mathcal {U}_0=\{\mathrm {int}\, U_{i}^{\delta /2} \mid i\in \mathcal {I}\}$
(recall equation (2.1)) and
![]() $\mathcal {D}_0=(\mathcal {I},\mathcal {U}_0,\varSigma , \delta _0,L,\lambda )$
. Obviously,
$\mathcal {D}_0=(\mathcal {I},\mathcal {U}_0,\varSigma , \delta _0,L,\lambda )$
. Obviously,
![]() $\mathcal {D}_0$
is an expansion datum of
$\mathcal {D}_0$
is an expansion datum of
![]() $\rho $
since
$\rho $
since
![]() $\mathcal {U}_0\prec \mathcal {U}$
and
$\mathcal {U}_0\prec \mathcal {U}$
and
![]() $\delta _0 <\delta $
. We take
$\delta _0 <\delta $
. We take
![]() $\mathcal {D}_0$
as the initial expansion datum of
$\mathcal {D}_0$
as the initial expansion datum of
![]() $\rho $
and claim that
$\rho $
and claim that
![]() $(\mathcal {D}_0\prec \mathcal {D}_{\delta /2};N_{\delta /2})$
is a uniform meandering hyperbolicity datum of
$(\mathcal {D}_0\prec \mathcal {D}_{\delta /2};N_{\delta /2})$
is a uniform meandering hyperbolicity datum of
![]() $\rho $
.
$\rho $
.
For
![]() $\eta \in (0,r_{\delta /2})$
, let
$\eta \in (0,r_{\delta /2})$
, let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be
$\beta $
be
![]() $(\mathcal {D}_0,\eta )$
-codes for
$(\mathcal {D}_0,\eta )$
-codes for
![]() $x\in \Lambda $
. Then, by the definition of
$x\in \Lambda $
. Then, by the definition of
![]() $\mathcal {U}_0$
, it can be easily seen that
$\mathcal {U}_0$
, it can be easily seen that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are
$\beta $
are
![]() $(\mathcal {D},\eta +\delta /2)$
-codes for x and hence
$(\mathcal {D},\eta +\delta /2)$
-codes for x and hence
![]() $(\mathcal {D},\delta /2)$
-codes for x. In other words, all
$(\mathcal {D},\delta /2)$
-codes for x. In other words, all
![]() $(\mathcal {D}_0,\eta )$
-codes are regarded as
$(\mathcal {D}_0,\eta )$
-codes are regarded as
![]() $(\mathcal {D},\delta /2)$
-codes for any
$(\mathcal {D},\delta /2)$
-codes for any
![]() $\eta \in (0,r_{\delta /2})$
. By the hypothesis, there is a finite chain of interpolating rays
$\eta \in (0,r_{\delta /2})$
. By the hypothesis, there is a finite chain of interpolating rays
![]() $c^{\alpha }=c^{\gamma _1}, c^{\gamma _2},\ldots , c^{\gamma _n}=c^{\beta }$
in
$c^{\alpha }=c^{\gamma _1}, c^{\gamma _2},\ldots , c^{\gamma _n}=c^{\beta }$
in
![]() $\mathrm {Ray}_x(\mathcal {D}_{\delta /2},r_{\delta /2})$
such that
$\mathrm {Ray}_x(\mathcal {D}_{\delta /2},r_{\delta /2})$
such that
Since
![]() $\eta <r_{\delta /2}$
, all the
$\eta <r_{\delta /2}$
, all the
![]() $(\mathcal {D}_{\delta /2},r_{\delta /2})$
-codes
$(\mathcal {D}_{\delta /2},r_{\delta /2})$
-codes
![]() $\gamma _i$
are
$\gamma _i$
are
![]() $(\mathcal {D}_{\delta /2},\eta )$
-codes. Hence, all rays in
$(\mathcal {D}_{\delta /2},\eta )$
-codes. Hence, all rays in
![]() $\mathrm {Ray}_x(\mathcal {D}_0,\eta )$
are
$\mathrm {Ray}_x(\mathcal {D}_0,\eta )$
are
![]() $(\mathcal {D}_{\delta /2},\eta ;N_{\delta /2})$
-equivalent. Furthermore, one can easily check that
$(\mathcal {D}_{\delta /2},\eta ;N_{\delta /2})$
-equivalent. Furthermore, one can easily check that
![]() $\mathcal {D}_0 \prec \mathcal {D}_{\delta /2}$
. Therefore, we conclude that
$\mathcal {D}_0 \prec \mathcal {D}_{\delta /2}$
. Therefore, we conclude that
![]() $(\mathcal {D}_0\prec \mathcal {D}_{\delta /2};N_{\delta /2})$
is a uniform meandering hyperbolicity datum of
$(\mathcal {D}_0\prec \mathcal {D}_{\delta /2};N_{\delta /2})$
is a uniform meandering hyperbolicity datum of
![]() $\rho $
.
$\rho $
.
5.2 Expansion
In order to obtain an expansion data for the
![]() $\Gamma $
-action on the flag manifold
$\Gamma $
-action on the flag manifold
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
, we proceed as in Remark 3.6(c). Roughly speaking, we will construct a finite open cover of
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
, we proceed as in Remark 3.6(c). Roughly speaking, we will construct a finite open cover of
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
whose elements are expanding subsets for some elements of
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
whose elements are expanding subsets for some elements of
![]() $\Gamma $
.
$\Gamma $
.
First, fix a number
![]() $\lambda>1$
and a base point
$\lambda>1$
and a base point
![]() $x\in X$
. Let
$x\in X$
. Let
![]() $D>0$
be the diameter of a compact fundamental domain for the
$D>0$
be the diameter of a compact fundamental domain for the
![]() $\Gamma $
-action on X. Then the orbit
$\Gamma $
-action on X. Then the orbit
![]() $\Gamma x \subset X$
is D-dense in X, that is,
$\Gamma x \subset X$
is D-dense in X, that is,
![]() $B_D(y)\cap \Gamma x \neq \emptyset $
for any
$B_D(y)\cap \Gamma x \neq \emptyset $
for any
![]() $y\in X$
. In view of [Reference Kapovich, Leeb and Porti26, Theorem 2.41], the D-density of
$y\in X$
. In view of [Reference Kapovich, Leeb and Porti26, Theorem 2.41], the D-density of
![]() $\Gamma x$
implies that for each
$\Gamma x$
implies that for each
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
, there is an element
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
, there is an element
![]() $g_{\tau }\in \Gamma $
such that
$g_{\tau }\in \Gamma $
such that
![]() $\mathcal E(g_{\tau }^{-1}, \tau )>\lambda $
. Define an open subset
$\mathcal E(g_{\tau }^{-1}, \tau )>\lambda $
. Define an open subset
![]() $U_{\tau }\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
by
$U_{\tau }\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
by
so that
![]() $\tau \in U_{\tau }$
and
$\tau \in U_{\tau }$
and
![]() $g^{-1}_{\tau }$
is
$g^{-1}_{\tau }$
is
![]() $(\lambda ,U_{\tau })$
-expanding. Then we have an open cover
$(\lambda ,U_{\tau })$
-expanding. Then we have an open cover
![]() $\{U_{\tau }\}_{\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})}$
of
$\{U_{\tau }\}_{\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})}$
of
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Since
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Since
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is compact, there is a finite subcover
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is compact, there is a finite subcover
![]() $\{U_{\tau _1},\ldots , U_{\tau _k}\}$
. For simplicity, let us abbreviate
$\{U_{\tau _1},\ldots , U_{\tau _k}\}$
. For simplicity, let us abbreviate
![]() $U_{\tau _i}$
and
$U_{\tau _i}$
and
![]() $g_{\tau _i}$
to
$g_{\tau _i}$
to
![]() $U_i$
and
$U_i$
and
![]() $g_i$
, respectively, for
$g_i$
, respectively, for
![]() $i=1,\ldots ,k$
.
$i=1,\ldots ,k$
.
By adding extra generators to
![]() $\{g_1,\ldots ,g_k\}$
with empty expanding subsets, we obtain a symmetric generating set
$\{g_1,\ldots ,g_k\}$
with empty expanding subsets, we obtain a symmetric generating set
![]() $\varSigma $
of
$\varSigma $
of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\mathcal {I}$
be the index set for
$\mathcal {I}$
be the index set for
![]() $\varSigma $
and
$\varSigma $
and
![]() $\mathcal {U}$
the collection of all
$\mathcal {U}$
the collection of all
![]() $(\lambda ,g_i^{-1})$
-expanding subsets
$(\lambda ,g_i^{-1})$
-expanding subsets
![]() $U_i$
, where
$U_i$
, where
![]() $g_i\in \varSigma $
. Since
$g_i\in \varSigma $
. Since
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is compact,
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is compact,
![]() $\varSigma $
is finite and the
$\varSigma $
is finite and the
![]() $\Gamma $
-action is by
$\Gamma $
-action is by
![]() $C^1$
-diffeomorphisms, there exist a constant
$C^1$
-diffeomorphisms, there exist a constant
![]() $L>1$
such that every
$L>1$
such that every
![]() $g_i\in \varSigma $
is L-Lipschitz on
$g_i\in \varSigma $
is L-Lipschitz on
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Let
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Let
![]() $\delta <\delta _{\mathcal {U}}$
be a Lebesgue number of
$\delta <\delta _{\mathcal {U}}$
be a Lebesgue number of
![]() $\mathcal {U}$
. Then
$\mathcal {U}$
. Then
![]() $\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
is an expansion datum of the
$\mathcal {D}=(\mathcal {I},\mathcal {U},\varSigma , \delta ,L,\lambda )$
is an expansion datum of the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
.
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
.
5.3 Coding rays are uniform Morse quasi-geodesics
In the proof of the next lemma, we will be using the notions of
![]() ${\tau _{\mathrm {mod}}}$
-regular (and uniformly regular) sequences and
${\tau _{\mathrm {mod}}}$
-regular (and uniformly regular) sequences and
![]() ${\tau _{\mathrm {mod}}}$
-convergence property for such sequences; the reader will find a detailed treatment of these notions in [Reference Kapovich, Leeb and Porti26, Section 4].
${\tau _{\mathrm {mod}}}$
-convergence property for such sequences; the reader will find a detailed treatment of these notions in [Reference Kapovich, Leeb and Porti26, Section 4].
Lemma 5.4. Let
![]() $\eta \in (0,\delta ]$
and
$\eta \in (0,\delta ]$
and
![]() $\alpha $
be a
$\alpha $
be a
![]() $(\mathcal {D},\eta )$
-code for
$(\mathcal {D},\eta )$
-code for
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
and
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
and
![]() $c^{\alpha }:\mathbb {N}_0\to \Gamma <G$
be the ray associated to
$c^{\alpha }:\mathbb {N}_0\to \Gamma <G$
be the ray associated to
![]() $\alpha $
. Then the sequence
$\alpha $
. Then the sequence
![]() $c^{\alpha } x$
in X is a
$c^{\alpha } x$
in X is a
![]() $(\Theta ,R)$
-Morse quasi-geodesic with end point
$(\Theta ,R)$
-Morse quasi-geodesic with end point
![]() $\tau $
for some data
$\tau $
for some data
![]() $(\Theta ,R)$
depending only on the pair
$(\Theta ,R)$
depending only on the pair
![]() $(\mathcal {D},\eta )$
.
$(\mathcal {D},\eta )$
.
Proof. Recall from Corollary 3.20 that the ray
![]() $c^{\alpha }$
is a uniform quasi-geodesic in
$c^{\alpha }$
is a uniform quasi-geodesic in
![]() $\Gamma $
which is quasi-isometric to X. Thus, in order to prove the Morse property, it suffices to establish the uniform
$\Gamma $
which is quasi-isometric to X. Thus, in order to prove the Morse property, it suffices to establish the uniform
![]() ${\tau _{\mathrm {mod}}}$
-regularity of the sequence
${\tau _{\mathrm {mod}}}$
-regularity of the sequence
![]() $c^{\alpha }$
; see [Reference Kapovich, Leeb and Porti27, Theorem 1.3].
$c^{\alpha }$
; see [Reference Kapovich, Leeb and Porti27, Theorem 1.3].
First of all, there exists a closed ball
![]() $B\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that
$B\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that
![]() $c^{\alpha }$
restricted to B subconverges uniformly to
$c^{\alpha }$
restricted to B subconverges uniformly to
![]() $\tau $
. Moreover, the limit set of a subsequence of
$\tau $
. Moreover, the limit set of a subsequence of
![]() $(c^{\alpha })^{-1}(\tau )$
lies in B by Theorem 3.21. Since B is Zariski dense in
$(c^{\alpha })^{-1}(\tau )$
lies in B by Theorem 3.21. Since B is Zariski dense in
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
, the sequence
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
, the sequence
![]() $c^{\alpha }$
is
$c^{\alpha }$
is
![]() ${\tau _{\mathrm {mod}}}$
-regular; see the proof of [Reference Kapovich and Leeb23, Theorem 9.6].
${\tau _{\mathrm {mod}}}$
-regular; see the proof of [Reference Kapovich and Leeb23, Theorem 9.6].
Now, we show that the sequence
![]() $c^{\alpha }$
is uniformly
$c^{\alpha }$
is uniformly
![]() ${\tau _{\mathrm {mod}}}$
-regular. We first verify that the sequence
${\tau _{\mathrm {mod}}}$
-regular. We first verify that the sequence
![]() $c^{\alpha }$
conically converges to
$c^{\alpha }$
conically converges to
![]() $\tau $
. Since it suffices to prove this for all subsequences in
$\tau $
. Since it suffices to prove this for all subsequences in
![]() $c^{\alpha }$
, we will freely pass to such subsequences. Note that the inverse sequence
$c^{\alpha }$
, we will freely pass to such subsequences. Note that the inverse sequence
![]() $(c^{\alpha })^{-1}$
is also
$(c^{\alpha })^{-1}$
is also
![]() $\iota {\tau _{\mathrm {mod}}}$
-regular and, hence, flag-subconverges to a simplex
$\iota {\tau _{\mathrm {mod}}}$
-regular and, hence, flag-subconverges to a simplex
![]() $\tau _-\in \mathrm {Flag}(\iota {\tau _{\mathrm {mod}}})$
. Furthermore, the sequence
$\tau _-\in \mathrm {Flag}(\iota {\tau _{\mathrm {mod}}})$
. Furthermore, the sequence
![]() $c^{\alpha }$
subconverges to
$c^{\alpha }$
subconverges to
![]() $\tau $
uniformly on compacts in the open Schubert cell
$\tau $
uniformly on compacts in the open Schubert cell
![]() $C(\tau _-)\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
of
$C(\tau _-)\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
of
![]() $\tau _-$
and, whenever
$\tau _-$
and, whenever
![]() $B'$
is a closed ball in
$B'$
is a closed ball in
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
which is not contained in
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
which is not contained in
![]() $C(\tau _-)$
, the sequence
$C(\tau _-)$
, the sequence
![]() $c^{\alpha }$
cannot subconverge to
$c^{\alpha }$
cannot subconverge to
![]() $\tau $
uniformly on
$\tau $
uniformly on
![]() $B'$
. Thus, the ball B, and hence its center
$B'$
. Thus, the ball B, and hence its center
![]() $\nu $
(which is the limit of a subsequence in
$\nu $
(which is the limit of a subsequence in
![]() $(c^{\alpha })^{-1}(\tau )$
), is contained in
$(c^{\alpha })^{-1}(\tau )$
), is contained in
![]() $C(\tau _-)$
. Since
$C(\tau _-)$
. Since
![]() $\nu \in C(\tau _-)$
, according to [Reference Kapovich, Leeb and Porti26, Proposition 5.31], the convergence
$\nu \in C(\tau _-)$
, according to [Reference Kapovich, Leeb and Porti26, Proposition 5.31], the convergence
![]() $c^{\alpha }\to \tau $
is conical.
$c^{\alpha }\to \tau $
is conical.
Lastly, by [Reference Kapovich, Leeb and Porti26, Theorem 2.41], the uniform exponential expansion of the sequence
![]() $(c^{\alpha })^{-1}$
at
$(c^{\alpha })^{-1}$
at
![]() $\tau $
(guaranteed by Lemma 3.14) implies (uniform)
$\tau $
(guaranteed by Lemma 3.14) implies (uniform)
![]() $\Theta $
-regularity of the sequence
$\Theta $
-regularity of the sequence
![]() $c^{\alpha }$
, where
$c^{\alpha }$
, where
![]() $\Theta $
is a certain fixed
$\Theta $
is a certain fixed
![]() $W_{\tau _{\mathrm {mod}}}$
-convex compact subset of the open star
$W_{\tau _{\mathrm {mod}}}$
-convex compact subset of the open star
![]() $\mathrm {ost}({\tau _{\mathrm {mod}}})$
of
$\mathrm {ost}({\tau _{\mathrm {mod}}})$
of
![]() ${\tau _{\mathrm {mod}}}$
in
${\tau _{\mathrm {mod}}}$
in
![]() ${\sigma _{\mathrm {mod}}}$
.
${\sigma _{\mathrm {mod}}}$
.
5.4 Morse interpolation
As in Definition 3.23, given two maps
![]() $p,q:\mathbb {R}_+\to X$
and an integer
$p,q:\mathbb {R}_+\to X$
and an integer
![]() $N\ge 0$
, we define the relation
$N\ge 0$
, we define the relation
![]() $p\approx ^N q$
by the condition that there exist unbounded monotonic sequences
$p\approx ^N q$
by the condition that there exist unbounded monotonic sequences
![]() $(P_k)$
and
$(P_k)$
and
![]() $(Q_j)$
in
$(Q_j)$
in
![]() $\mathbb {R}_+$
such that the subsets
$\mathbb {R}_+$
such that the subsets
![]() $\{p(P_k)\mid k\in \mathbb {N}_0\}$
and
$\{p(P_k)\mid k\in \mathbb {N}_0\}$
and
![]() $\{q(Q_j)\mid j\in \mathbb {N}_0\}$
in X are within Hausdorff distance N from each other.
$\{q(Q_j)\mid j\in \mathbb {N}_0\}$
in X are within Hausdorff distance N from each other.
Lemma 5.5. Let p and q be
![]() $(\Theta ,R)$
-Morse quasi-geodesic rays in X with
$(\Theta ,R)$
-Morse quasi-geodesic rays in X with
![]() $p(\infty )=q(\infty )=\tau $
. Let
$p(\infty )=q(\infty )=\tau $
. Let
![]() $\Theta '\subset \mathrm {ost}({\tau _{\mathrm {mod}}})$
be a
$\Theta '\subset \mathrm {ost}({\tau _{\mathrm {mod}}})$
be a
![]() $W_{\tau _{\mathrm {mod}}}$
-convex compact subset such that
$W_{\tau _{\mathrm {mod}}}$
-convex compact subset such that
![]() $\Theta \subset \mathrm {int}(\Theta ')$
. Given a constant
$\Theta \subset \mathrm {int}(\Theta ')$
. Given a constant
![]() $l>0$
, there is a
$l>0$
, there is a
![]() $(\Theta ',R)$
-Morse quasi-geodesic ray r with end point
$(\Theta ',R)$
-Morse quasi-geodesic ray r with end point
![]() $r(\infty )=\tau $
in X such that
$r(\infty )=\tau $
in X such that
-
(i)
 $r(t_n) \in p(\mathbb {R}_+)$
if n is odd and
$r(t_n) \in p(\mathbb {R}_+)$
if n is odd and
 $r(t_n) \in q(\mathbb {R}_+)$
if n is even, and hence
$r(t_n) \in q(\mathbb {R}_+)$
if n is even, and hence
 $p\approx ^0 r\approx ^0 q$
,
$p\approx ^0 r\approx ^0 q$
, -
(ii) the restriction of r to each interval
 $[t_n, t_{n+1}]$
is a
$[t_n, t_{n+1}]$
is a
 $\Theta '$
-regular geodesic,
$\Theta '$
-regular geodesic, -
(iii)
 $d_X(r(t_n),r(t_{n+1}))\geq l$
for all integers
$d_X(r(t_n),r(t_{n+1}))\geq l$
for all integers
 $n\geq 0$
.
$n\geq 0$
.
Moreover, if
![]() $p(0)=q(0)=x\in X$
, then r can be chosen such that
$p(0)=q(0)=x\in X$
, then r can be chosen such that
![]() $r(0)=x$
.
$r(0)=x$
.

Figure 4 Interpolating ray.
Proof. According to [Reference Kapovich, Leeb and Porti26, Lemma 5.52], both p and q are contained in the R-neighborhood of a cone
![]() $V=V(x,\mathrm {st}(\tau ))$
. We define the points
$V=V(x,\mathrm {st}(\tau ))$
. We define the points
![]() $r(t_n)$
inductively as follows (see Figure 4). Set
$r(t_n)$
inductively as follows (see Figure 4). Set
![]() $t_0=0$
and
$t_0=0$
and
![]() $r(0)=q(0)$
. Suppose that n is odd and
$r(0)=q(0)$
. Suppose that n is odd and
![]() $r(t_n)\in p(\mathbb {R}_+)$
is defined. Since the Morse quasi-geodesic ray q is
$r(t_n)\in p(\mathbb {R}_+)$
is defined. Since the Morse quasi-geodesic ray q is
![]() $\Theta $
-regular, the limit (as
$\Theta $
-regular, the limit (as
![]() $t\to \infty $
) of directions of oriented segments
$t\to \infty $
) of directions of oriented segments
belongs to
![]() $\mathrm {st}_{\Theta }(\tau )$
. Therefore, for a sufficiently large
$\mathrm {st}_{\Theta }(\tau )$
. Therefore, for a sufficiently large
![]() $s_n>0$
, the directions of both geodesic segments
$s_n>0$
, the directions of both geodesic segments
![]() $r(t_n)q(s_n)$
and
$r(t_n)q(s_n)$
and
![]() $\bar r(t_n)\bar q(s_n)$
are in the interior of
$\bar r(t_n)\bar q(s_n)$
are in the interior of
![]() $\mathrm {st}_{\Theta '}(\tau )$
and
$\mathrm {st}_{\Theta '}(\tau )$
and
![]() $d_X(r(t_n),q(s_n))>l$
, where
$d_X(r(t_n),q(s_n))>l$
, where
![]() $\bar r(t)$
and
$\bar r(t)$
and
![]() $\bar q(t)$
are the nearest projections of
$\bar q(t)$
are the nearest projections of
![]() $r(t)$
and
$r(t)$
and
![]() $q(t)$
onto V, respectively. Then we set
$q(t)$
onto V, respectively. Then we set
![]() $t_{n+1}=t_n+d_X(r(t_n),q(s_n))$
and
$t_{n+1}=t_n+d_X(r(t_n),q(s_n))$
and
![]() $r(t_{n+1})=q(t_{n+1}$
). When n is even and
$r(t_{n+1})=q(t_{n+1}$
). When n is even and
![]() $r(t_n)\in q(\mathbb {R}_+)$
, the point
$r(t_n)\in q(\mathbb {R}_+)$
, the point
![]() $r(t_{n+1})$
is defined in the same way.
$r(t_{n+1})$
is defined in the same way.
Since the cone V is convex in X, the piecewise geodesic ray
![]() $\bar r :[0,\infty )\to V$
with vertices
$\bar r :[0,\infty )\to V$
with vertices
![]() $(\bar r(t_n))_{n\in \mathbb {N}_0}$
is a geodesic ray whose restriction to each interval
$(\bar r(t_n))_{n\in \mathbb {N}_0}$
is a geodesic ray whose restriction to each interval
![]() $[t_n,t_{n+1}]$
is
$[t_n,t_{n+1}]$
is
![]() $\Theta '$
-regular and longitudinal. By the nestedness property of
$\Theta '$
-regular and longitudinal. By the nestedness property of
![]() $\Theta '$
-cones (see [Reference Kapovich, Leeb and Porti26, Section 2.12]), the entire ray
$\Theta '$
-cones (see [Reference Kapovich, Leeb and Porti26, Section 2.12]), the entire ray
![]() $\bar r$
is a
$\bar r$
is a
![]() $\Theta '$
-Finsler geodesic ray in V. Then the piecewise geodesic ray r with vertices
$\Theta '$
-Finsler geodesic ray in V. Then the piecewise geodesic ray r with vertices
![]() $(r(t_n))_{n\in \mathbb {N}_0}$
is R-Hausdorff close to the
$(r(t_n))_{n\in \mathbb {N}_0}$
is R-Hausdorff close to the
![]() $\Theta '$
-Finsler geodesic ray
$\Theta '$
-Finsler geodesic ray
![]() $\bar r$
. Therefore, the ray r is a
$\bar r$
. Therefore, the ray r is a
![]() $(\Theta ',R)$
-Morse quasi-geodesic ray. From the above construction, the ray r clearly satisfies
$(\Theta ',R)$
-Morse quasi-geodesic ray. From the above construction, the ray r clearly satisfies
![]() $r(\infty )=\tau $
as well as (i), (ii) and (iii) of the lemma.
$r(\infty )=\tau $
as well as (i), (ii) and (iii) of the lemma.
5.5 Refined expansion data
Now, we find a refinement
![]() $\mathcal {D}_{\eta }$
of the expansion datum
$\mathcal {D}_{\eta }$
of the expansion datum
![]() $\mathcal {D}$
for each
$\mathcal {D}$
for each
![]() $\eta \in (0,\delta ]$
.
$\eta \in (0,\delta ]$
.
Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be
$\beta $
be
![]() $(\mathcal {D},\eta )$
-codes for
$(\mathcal {D},\eta )$
-codes for
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
. By Lemma 5.4, the associated rays
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
. By Lemma 5.4, the associated rays
![]() $c^{\alpha }$
and
$c^{\alpha }$
and
![]() $c^{\beta }$
project in X to
$c^{\beta }$
project in X to
![]() $(\Theta ,R)$
-Morse quasi-geodesic rays with end point
$(\Theta ,R)$
-Morse quasi-geodesic rays with end point
![]() $\tau $
, where the datum
$\tau $
, where the datum
![]() $(\Theta ,R)$
depends only on
$(\Theta ,R)$
depends only on
![]() $\mathcal {D}$
and
$\mathcal {D}$
and
![]() $\eta $
. Hence,
$\eta $
. Hence,
![]() $c^{\alpha }(n)x$
and
$c^{\alpha }(n)x$
and
![]() $c^{\beta }(n)x$
are contained in the R-neighborhood of
$c^{\beta }(n)x$
are contained in the R-neighborhood of
![]() $V(x, \text {st}_{\Theta }(\tau ))$
for any integer
$V(x, \text {st}_{\Theta }(\tau ))$
for any integer
![]() $n\geq 0$
. We fix compact
$n\geq 0$
. We fix compact
![]() $W_{\tau _{\mathrm {mod}}}$
-convex subsets
$W_{\tau _{\mathrm {mod}}}$
-convex subsets
![]() $\Theta ', \Theta "\subset \text {ost}({\tau _{\mathrm {mod}}})$
in
$\Theta ', \Theta "\subset \text {ost}({\tau _{\mathrm {mod}}})$
in
![]() ${\sigma _{\mathrm {mod}}}$
such that
${\sigma _{\mathrm {mod}}}$
such that
We first choose a constant l such that
where the constants
![]() $l_1$
,
$l_1$
,
![]() $l_2$
and
$l_2$
and
![]() $l_3$
are defined as follows. First, choose a constant
$l_3$
are defined as follows. First, choose a constant
![]() $l_1=l_1(\Theta ',\Theta ", D,R)>0$
so that, if
$l_1=l_1(\Theta ',\Theta ", D,R)>0$
so that, if
![]() $d_{\Delta }(x,y)\in V(0, W_{{\tau _{\mathrm {mod}}}}\Theta ')\cap \Delta $
and
$d_{\Delta }(x,y)\in V(0, W_{{\tau _{\mathrm {mod}}}}\Theta ')\cap \Delta $
and
![]() $d_X(x,y)>l_1$
, then
$d_X(x,y)>l_1$
, then
for any
![]() $x'\in B_{D+R}(x)$
and any
$x'\in B_{D+R}(x)$
and any
![]() $y'\in B_{D+R}(y)$
. This is possible due to the following inequality
$y'\in B_{D+R}(y)$
. This is possible due to the following inequality
For the second constant
![]() $l_2>0$
, we recall [Reference Kapovich, Leeb and Porti26, Theorem 2.41] again that there are constants
$l_2>0$
, we recall [Reference Kapovich, Leeb and Porti26, Theorem 2.41] again that there are constants
![]() $C, A>0$
depending only on
$C, A>0$
depending only on
![]() $x, R, D$
and the chosen Riemannian metric on
$x, R, D$
and the chosen Riemannian metric on
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that if
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that if
![]() $d_X(gx,V(x,\mathrm {st}(\tau )))\le 2(D+R)$
, then
$d_X(gx,V(x,\mathrm {st}(\tau )))\le 2(D+R)$
, then
where
![]() $\partial V(x,\mathrm {st}(\tau )))$
is the boundary of
$\partial V(x,\mathrm {st}(\tau )))$
is the boundary of
![]() $V(x,\mathrm {st}(\tau )))$
in X. (Recall from equation (2.2) that
$V(x,\mathrm {st}(\tau )))$
in X. (Recall from equation (2.2) that
![]() $\mathcal E(g^{-1},\tau )$
is the expansion factor of
$\mathcal E(g^{-1},\tau )$
is the expansion factor of
![]() $g^{-1}$
at
$g^{-1}$
at
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
). Given
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
). Given
![]() $\lambda>1$
, the inequality (5.7) makes it possible to choose a constant
$\lambda>1$
, the inequality (5.7) makes it possible to choose a constant
![]() $l_2=l_2(x,R,D,\lambda )>0$
such that if
$l_2=l_2(x,R,D,\lambda )>0$
such that if
![]() $d_X(gx, \partial V(x,\mathrm {st}(\tau )))\geq l_2$
and
$d_X(gx, \partial V(x,\mathrm {st}(\tau )))\geq l_2$
and
![]() $d_X(gx, V(x, \text {st}(\tau )))\leq 2(D+R)$
, then
$d_X(gx, V(x, \text {st}(\tau )))\leq 2(D+R)$
, then
![]() $\mathcal E(g^{-1},\tau )\geq 2\lambda $
.
$\mathcal E(g^{-1},\tau )\geq 2\lambda $
.
Finally, we choose a constant
![]() $l_3>0$
as follows: If
$l_3>0$
as follows: If
![]() $y\in V(x,\mathrm {st}_{\Theta "}(\tau ))$
, the distance of y from
$y\in V(x,\mathrm {st}_{\Theta "}(\tau ))$
, the distance of y from
![]() $\partial V(x,\mathrm {st}(\tau ))$
grows linearly with the distance of x and y. Its linear growth rate only depends on
$\partial V(x,\mathrm {st}(\tau ))$
grows linearly with the distance of x and y. Its linear growth rate only depends on
![]() $\Theta "$
, and hence there is a constant
$\Theta "$
, and hence there is a constant
![]() $l_3=l_3(\Theta ",l_2)>0$
such that, if
$l_3=l_3(\Theta ",l_2)>0$
such that, if
![]() $y\in V(x,\mathrm {st}_{\Theta "}(\tau ))$
and
$y\in V(x,\mathrm {st}_{\Theta "}(\tau ))$
and
![]() $d_X(x,y)> l_3$
, then
$d_X(x,y)> l_3$
, then
![]() $d_X(y, \partial V(x,\mathrm {st}(\tau )))> l_2+2(D+R)$
for any
$d_X(y, \partial V(x,\mathrm {st}(\tau )))> l_2+2(D+R)$
for any
![]() $x,y\in X$
and any
$x,y\in X$
and any
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
.
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
.
Now, we are ready to add new generators to
![]() $\varSigma $
. Let
$\varSigma $
. Let
![]() $\varSigma _0$
be the set of all elements
$\varSigma _0$
be the set of all elements
![]() $g\in \Gamma $
such that
$g\in \Gamma $
such that
Since
![]() $\Gamma $
acts properly discontinuously on X,
$\Gamma $
acts properly discontinuously on X,
![]() $\varSigma _0$
is finite. To each
$\varSigma _0$
is finite. To each
![]() $g\in \varSigma _0$
, we associate its expansion domain
$g\in \varSigma _0$
, we associate its expansion domain
Add all elements
![]() $g\in \varSigma _0$
together with
$g\in \varSigma _0$
together with
![]() $\lambda $
-expanding domains
$\lambda $
-expanding domains
![]() $U^{\lambda }_g$
to
$U^{\lambda }_g$
to
![]() $\varSigma $
and
$\varSigma $
and
![]() $\mathcal {U}$
, respectively. Furthermore, if necessary, add the inverses of
$\mathcal {U}$
, respectively. Furthermore, if necessary, add the inverses of
![]() $\varSigma _0$
together with their (possibly empty)
$\varSigma _0$
together with their (possibly empty)
![]() $\lambda $
-expanding domains. Then we obtain a symmetric generating finite set
$\lambda $
-expanding domains. Then we obtain a symmetric generating finite set
![]() $\varSigma _{\eta }$
and the collection
$\varSigma _{\eta }$
and the collection
![]() $\mathcal {U}_{\eta }$
of all
$\mathcal {U}_{\eta }$
of all
![]() $(\lambda ,g)$
-expanding subsets for
$(\lambda ,g)$
-expanding subsets for
![]() $g\in \varSigma _{\eta }$
. The index set
$g\in \varSigma _{\eta }$
. The index set
![]() $\mathcal {I}_{\eta }$
for
$\mathcal {I}_{\eta }$
for
![]() $\varSigma _{\eta }$
, and the Lipschitz constant
$\varSigma _{\eta }$
, and the Lipschitz constant
![]() $L_{\eta } \ge L$
are determined in the obvious way. Lastly, by setting
$L_{\eta } \ge L$
are determined in the obvious way. Lastly, by setting
 $$ \begin{align} \delta_{\eta}:=\min\left\{\frac{99}{100}\eta,\;\min_{\substack{g\in\varSigma_0 \\ U^{2\lambda}_g \neq \emptyset}} d_X(U^{2\lambda}_g,\partial U^{\lambda}_g) \right\}<\eta\le\delta, \end{align} $$
$$ \begin{align} \delta_{\eta}:=\min\left\{\frac{99}{100}\eta,\;\min_{\substack{g\in\varSigma_0 \\ U^{2\lambda}_g \neq \emptyset}} d_X(U^{2\lambda}_g,\partial U^{\lambda}_g) \right\}<\eta\le\delta, \end{align} $$
we obtain a refined expansion datum
for the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Note that by the definition of
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Note that by the definition of
![]() $\delta _{\eta }$
, if
$\delta _{\eta }$
, if
![]() $\tau \in U_g^{2\lambda }$
for some
$\tau \in U_g^{2\lambda }$
for some
![]() $g\in \varSigma _0$
, then
$g\in \varSigma _0$
, then
![]() $B_{\delta _{\eta }}(\tau )\subset U^{\lambda }_g$
.
$B_{\delta _{\eta }}(\tau )\subset U^{\lambda }_g$
.
5.6 Uniform meandering hyperbolicity
Lastly, we are left with checking the uniform meandering hyperbolicity condition.
Fix
![]() $\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Let
$\tau \in \mathrm {Flag}({\tau _{\mathrm {mod}}})$
. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be
$\beta $
be
![]() $(\mathcal {D},\eta )$
-codes for
$(\mathcal {D},\eta )$
-codes for
![]() $\tau $
. In view of Proposition 5.3, it suffices to show that the associated rays
$\tau $
. In view of Proposition 5.3, it suffices to show that the associated rays
![]() $c^{\alpha }$
and
$c^{\alpha }$
and
![]() $c^{\beta }$
are
$c^{\beta }$
are
![]() $(\mathcal {D}_{\eta },\delta _{\eta };N)$
-equivalent for some integer
$(\mathcal {D}_{\eta },\delta _{\eta };N)$
-equivalent for some integer
![]() $N\ge 1$
. But we claim, as a matter of fact, that there exists a
$N\ge 1$
. But we claim, as a matter of fact, that there exists a
![]() $(\mathcal {D}_{\eta },\delta _{\eta })$
-code
$(\mathcal {D}_{\eta },\delta _{\eta })$
-code
![]() $\gamma $
for
$\gamma $
for
![]() $\tau $
such that
$\tau $
such that
That is to say, the rays
![]() $c^{\alpha }$
and
$c^{\alpha }$
and
![]() $c^{\beta }$
are
$c^{\beta }$
are
![]() $(\mathcal {D}_{\eta },\delta _{\eta };0)$
-equivalent, and hence
$(\mathcal {D}_{\eta },\delta _{\eta };0)$
-equivalent, and hence
![]() $(\mathcal {D}_{\eta },\delta _{\eta };1)$
-equivalent.
$(\mathcal {D}_{\eta },\delta _{\eta };1)$
-equivalent.
Let us prove the claim. By Lemma 5.4, the sequences
![]() $c^{\alpha } x$
and
$c^{\alpha } x$
and
![]() $c^{\beta } x$
are
$c^{\beta } x$
are
![]() $(\Theta ,R)$
-Morse quasi-geodesic rays in
$(\Theta ,R)$
-Morse quasi-geodesic rays in
![]() $\Gamma x$
with end point
$\Gamma x$
with end point
![]() $\tau $
for a uniform datum
$\tau $
for a uniform datum
![]() $(\Theta ,R)$
depending only on
$(\Theta ,R)$
depending only on
![]() $(\mathcal {D},\eta )$
. Then both
$(\mathcal {D},\eta )$
. Then both
![]() $c^{\alpha } x$
and
$c^{\alpha } x$
and
![]() $c^{\beta } x$
are contained in the R-neighborhood of a cone
$c^{\beta } x$
are contained in the R-neighborhood of a cone
![]() $V(x,\mathrm {st}(\tau ))$
. We fix compact
$V(x,\mathrm {st}(\tau ))$
. We fix compact
![]() $W_{\tau _{\mathrm {mod}}}$
-convex subsets
$W_{\tau _{\mathrm {mod}}}$
-convex subsets
![]() $\Theta ', \Theta "\subset \text {ost}({\tau _{\mathrm {mod}}})\subset {\sigma _{\mathrm {mod}}}$
such that
$\Theta ', \Theta "\subset \text {ost}({\tau _{\mathrm {mod}}})\subset {\sigma _{\mathrm {mod}}}$
such that
![]() $\Theta \subset \text {int}(\Theta ') \subset \Theta ' \subset \mathrm {int}(\Theta ")$
. Applying Lemma 5.5 with the chosen constant
$\Theta \subset \text {int}(\Theta ') \subset \Theta ' \subset \mathrm {int}(\Theta ")$
. Applying Lemma 5.5 with the chosen constant
![]() $l>0$
in equation (5.6), there is a
$l>0$
in equation (5.6), there is a
![]() $(\Theta ',R)$
-Morse quasi-geodesic r in
$(\Theta ',R)$
-Morse quasi-geodesic r in
![]() $\Gamma x$
with
$\Gamma x$
with
![]() $r(0)=x$
and
$r(0)=x$
and
![]() $r(\infty )=\tau $
and an unbounded increasing sequence
$r(\infty )=\tau $
and an unbounded increasing sequence
![]() $t_n\in \mathbb {R}_+$
such that the properties (i), (ii) and (iii) of the lemma hold. According to the proof of Lemma 5.5, we may assume that
$t_n\in \mathbb {R}_+$
such that the properties (i), (ii) and (iii) of the lemma hold. According to the proof of Lemma 5.5, we may assume that
![]() $r(t_n)\in c^{\alpha }(\mathbb {N}_0)x$
if n is odd and
$r(t_n)\in c^{\alpha }(\mathbb {N}_0)x$
if n is odd and
![]() $r(t_n)\in c^{\beta }(\mathbb {N}_0)x$
if n is even, and the piecewise geodesic ray with vertices
$r(t_n)\in c^{\beta }(\mathbb {N}_0)x$
if n is even, and the piecewise geodesic ray with vertices
![]() $(\bar r(t_n))_{n\in \mathbb {N}_0}$
is a
$(\bar r(t_n))_{n\in \mathbb {N}_0}$
is a
![]() $\Theta '$
-Finsler geodesic ray in
$\Theta '$
-Finsler geodesic ray in
![]() $V(x, st(\tau ))$
.
$V(x, st(\tau ))$
.
The properties (ii) and (iii) of Lemma 5.5 imply that
![]() $t_{n+1}-t_n>l$
for every
$t_{n+1}-t_n>l$
for every
![]() $n\in \mathbb {N}_0$
. For each
$n\in \mathbb {N}_0$
. For each
![]() $n\in \mathbb {N}_0$
, set
$n\in \mathbb {N}_0$
, set
 $$\begin{align*}k_n=\left \lfloor \frac{t_{n+1}-t_n}{l} \right \rfloor -1. \end{align*}$$
$$\begin{align*}k_n=\left \lfloor \frac{t_{n+1}-t_n}{l} \right \rfloor -1. \end{align*}$$
Let
![]() $(u_k)_{k\in \mathbb {N}_0}$
be an increasing sequence consisting of
$(u_k)_{k\in \mathbb {N}_0}$
be an increasing sequence consisting of
![]() $\{t_n+jl \mid n\in \mathbb {N}_0, \ j=0,\ldots ,k_n \}$
. Then it is easy to see that
$\{t_n+jl \mid n\in \mathbb {N}_0, \ j=0,\ldots ,k_n \}$
. Then it is easy to see that
![]() $(t_k)$
is a subsequence of
$(t_k)$
is a subsequence of
![]() $(u_k)$
and for every
$(u_k)$
and for every
![]() $k\in \mathbb {N}_0$
,
$k\in \mathbb {N}_0$
,
For a sufficiently large l, we may assume that the piecewise geodesic ray with vertices
![]() $(\bar r(u_k))_{k\in \mathbb {N}_0}$
is a
$(\bar r(u_k))_{k\in \mathbb {N}_0}$
is a
![]() $\Theta "$
-Finsler geodesic ray. This is possible since r is a
$\Theta "$
-Finsler geodesic ray. This is possible since r is a
![]() $(\Theta ',R)$
-Morse quasi-geodesic. For the proof, we refer the reader to [Reference Kapovich, Leeb and Porti26, Theorem 5.53].
$(\Theta ',R)$
-Morse quasi-geodesic. For the proof, we refer the reader to [Reference Kapovich, Leeb and Porti26, Theorem 5.53].
Due to the D-density of
![]() $\Gamma x$
in X, for each
$\Gamma x$
in X, for each
![]() $r(u_k)$
there exists an element
$r(u_k)$
there exists an element
![]() $g_k\in \Gamma $
such that
$g_k\in \Gamma $
such that
![]() $g_k x \in B_D(r(u_k))$
. Here, we require that if
$g_k x \in B_D(r(u_k))$
. Here, we require that if
![]() $r(u_k)\in c^{\alpha } (\mathbb {N}_0)x$
(resp.
$r(u_k)\in c^{\alpha } (\mathbb {N}_0)x$
(resp.
![]() $r(u_k)\in c^{\beta } (\mathbb {N}_0)x$
), then
$r(u_k)\in c^{\beta } (\mathbb {N}_0)x$
), then
![]() $g_k \in c^{\alpha }(\mathbb {N}_0)$
(resp.
$g_k \in c^{\alpha }(\mathbb {N}_0)$
(resp.
![]() $g_k\in c^{\beta } (\mathbb {N}_0)$
) and
$g_k\in c^{\beta } (\mathbb {N}_0)$
) and
![]() $g_0=e$
. This gives us that
$g_0=e$
. This gives us that
![]() $g_{k}\in c^{\alpha }(\mathbb {N}_0)$
if
$g_{k}\in c^{\alpha }(\mathbb {N}_0)$
if
![]() $u_k=t_n$
for an odd number n and
$u_k=t_n$
for an odd number n and
![]() $g_{k}\in c^{\beta }(\mathbb {N}_0)$
if
$g_{k}\in c^{\beta }(\mathbb {N}_0)$
if
![]() $u_k=t_n$
for an even number n. Thus,
$u_k=t_n$
for an even number n. Thus,
![]() $\{g_k\mid k\in \mathbb {N}_0\}$
has infinitely many elements of both
$\{g_k\mid k\in \mathbb {N}_0\}$
has infinitely many elements of both
![]() $c^{\alpha }(\mathbb {N}_0)$
and
$c^{\alpha }(\mathbb {N}_0)$
and
![]() $c^{\beta }(\mathbb {N}_0)$
.
$c^{\beta }(\mathbb {N}_0)$
.
We will show that there is a
![]() $(\mathcal {D}_{\eta },\delta _{\eta })$
-code
$(\mathcal {D}_{\eta },\delta _{\eta })$
-code
![]() $\gamma $
for
$\gamma $
for
![]() $\tau $
such that
$\tau $
such that
![]() $c^{\gamma }(k)=g_{k+1}$
for
$c^{\gamma }(k)=g_{k+1}$
for
![]() $k\in \mathbb {N}_0$
. Then (5.10) will immediately follow.
$k\in \mathbb {N}_0$
. Then (5.10) will immediately follow.
Lemma 5.12. Let
![]() $h_k=g_k^{-1}g_{k+1}$
for
$h_k=g_k^{-1}g_{k+1}$
for
![]() $k\in \mathbb {N}_0$
. Then
$k\in \mathbb {N}_0$
. Then
![]() $h_k \in \varSigma _{\eta }$
and
$h_k \in \varSigma _{\eta }$
and
![]() $\mathcal E(h_k^{-1}, h_{k-1}^{-1}\cdots h_0^{-1}\tau )>2\lambda $
for every
$\mathcal E(h_k^{-1}, h_{k-1}^{-1}\cdots h_0^{-1}\tau )>2\lambda $
for every
![]() $k\in \mathbb {N}_0$
.
$k\in \mathbb {N}_0$
.
Proof. To show that
![]() $h_k =g_k^{-1}g_{k+1} \in \varSigma _{\eta }$
, we need to verify (5.8). From the facts that
$h_k =g_k^{-1}g_{k+1} \in \varSigma _{\eta }$
, we need to verify (5.8). From the facts that
![]() $g_k x \in B_D(r(u_k))$
,
$g_k x \in B_D(r(u_k))$
,
![]() $\bar r(u_k) \in B_R(r(u_k))$
and (5.11), it easily follows that
$\bar r(u_k) \in B_R(r(u_k))$
and (5.11), it easily follows that
Moreover, since the geodesic
![]() $r(u_k) r(u_{k+1})$
is a
$r(u_k) r(u_{k+1})$
is a
![]() $\Theta '$
-regular geodesic of length at least
$\Theta '$
-regular geodesic of length at least
![]() $l>l_1$
and
$l>l_1$
and
![]() $g_k x \in B_D(r(u_k))\subset B_{D+R}(r(u_k))$
for all
$g_k x \in B_D(r(u_k))\subset B_{D+R}(r(u_k))$
for all
![]() $k\in \mathbb {N}_0$
, the definition of
$k\in \mathbb {N}_0$
, the definition of
![]() $l_1$
gives
$l_1$
gives
Thus, every
![]() $h_k$
is an element of
$h_k$
is an element of
![]() $\varSigma _{\eta }$
.
$\varSigma _{\eta }$
.
Now,we will prove the second statement
![]() $\mathcal E(h_k^{-1}, h_{k-1}^{-1}\cdots h_0^{-1}\tau )>2\lambda $
. An easy computation gives that
$\mathcal E(h_k^{-1}, h_{k-1}^{-1}\cdots h_0^{-1}\tau )>2\lambda $
. An easy computation gives that
![]() $h_{k-1}^{-1}\cdots h_0^{-1}=g_k^{-1}g_0=g_k^{-1}$
, and hence
$h_{k-1}^{-1}\cdots h_0^{-1}=g_k^{-1}g_0=g_k^{-1}$
, and hence
One can estimate the expansion factor
![]() $\mathcal E((g_{k}^{-1}g_{k+1})^{-1}, g_k^{-1}\tau )$
through the distances from
$\mathcal E((g_{k}^{-1}g_{k+1})^{-1}, g_k^{-1}\tau )$
through the distances from
![]() $g_k^{-1}g_{k+1}x$
to the Weyl cone
$g_k^{-1}g_{k+1}x$
to the Weyl cone
![]() $V(x, \mathrm {st}(g_k^{-1}\tau ))$
and its boundary
$V(x, \mathrm {st}(g_k^{-1}\tau ))$
and its boundary
![]() $\partial V(x, \mathrm {st}(g_k^{-1}\tau ))$
as follows. The conditions of
$\partial V(x, \mathrm {st}(g_k^{-1}\tau ))$
as follows. The conditions of
![]() $g_k x \in B_D(r(u_k))$
and
$g_k x \in B_D(r(u_k))$
and
![]() $\bar r(u_k) \in B_R(r(u_k))$
yields
$\bar r(u_k) \in B_R(r(u_k))$
yields
The fact that the piecewise geodesic ray with vertices
![]() $\bar r(u_k)$
is a
$\bar r(u_k)$
is a
![]() $\Theta "$
-Finsler geodesic ray in
$\Theta "$
-Finsler geodesic ray in
![]() $V(x,\mathrm {st}(\tau ))$
implies
$V(x,\mathrm {st}(\tau ))$
implies
![]() $\bar r(u_{k+1}) \in V(\bar r(u_k), \mathrm {st}_{\Theta "}(\tau ))\subset V(\bar r(u_{k}), \mathrm {st}(\tau ))$
. Thus,
$\bar r(u_{k+1}) \in V(\bar r(u_k), \mathrm {st}_{\Theta "}(\tau ))\subset V(\bar r(u_{k}), \mathrm {st}(\tau ))$
. Thus,
 $$ \begin{align*} d_X(g_{k+1} x, V(g_k x, \mathrm{st}(\tau))) & \leq d_X(g_{k+1} x, \bar r(u_{k+1}))+d_X(\bar r(u_{k+1}), V(g_k x, \mathrm{st}(\tau))) \\ & \leq d_X(g_{k+1} x, \bar r(u_{k+1}))+d_H(V(\bar r(u_{k}), \mathrm{st}(\tau)), V(g_kx, \mathrm{st}(\tau))) \\ & \leq d_X(g_{k+1} x, \bar r(u_{k+1}))+d_X(g_kx,\bar r(u_k)) \\ & \leq 2(D+R), \end{align*} $$
$$ \begin{align*} d_X(g_{k+1} x, V(g_k x, \mathrm{st}(\tau))) & \leq d_X(g_{k+1} x, \bar r(u_{k+1}))+d_X(\bar r(u_{k+1}), V(g_k x, \mathrm{st}(\tau))) \\ & \leq d_X(g_{k+1} x, \bar r(u_{k+1}))+d_H(V(\bar r(u_{k}), \mathrm{st}(\tau)), V(g_kx, \mathrm{st}(\tau))) \\ & \leq d_X(g_{k+1} x, \bar r(u_{k+1}))+d_X(g_kx,\bar r(u_k)) \\ & \leq 2(D+R), \end{align*} $$
where
![]() $d_H$
denotes Hausdorff distance between subsets of X. The third inequality above follows from the fact that the Hausdorff distance between
$d_H$
denotes Hausdorff distance between subsets of X. The third inequality above follows from the fact that the Hausdorff distance between
![]() $V(y,\mathrm {st}(\tau ))$
and
$V(y,\mathrm {st}(\tau ))$
and
![]() $V(y', \mathrm {st}(\tau ))$
is bounded above by
$V(y', \mathrm {st}(\tau ))$
is bounded above by
![]() $d_X(y,y')$
.
$d_X(y,y')$
.
Next, we estimate the distance between
![]() $g_k^{-1}g_{k+1}x$
and
$g_k^{-1}g_{k+1}x$
and
![]() $\partial V(x, \mathrm {st}(g_k^{-1}\tau ))$
. From the inequalities (5.13) and (5.14),
$\partial V(x, \mathrm {st}(g_k^{-1}\tau ))$
. From the inequalities (5.13) and (5.14),
Since
![]() $\bar r(u_{k+1}) \in V( \bar r(u_{k}),\mathrm {st}_{\Theta "}(\tau ))$
, it follows from the definition of
$\bar r(u_{k+1}) \in V( \bar r(u_{k}),\mathrm {st}_{\Theta "}(\tau ))$
, it follows from the definition of
![]() $l_3$
that
$l_3$
that
Let
![]() $p_{k}$
be the point on
$p_{k}$
be the point on
![]() $\partial V(g_kx,\mathrm {st}(\tau ))$
, where
$\partial V(g_kx,\mathrm {st}(\tau ))$
, where
![]() $d_X(g_{k+1}x, \partial V(g_kx, \mathrm {st}(\tau )))$
is realized. If we denote by
$d_X(g_{k+1}x, \partial V(g_kx, \mathrm {st}(\tau )))$
is realized. If we denote by
![]() $c_{y}^{\xi }:[0,\infty )\to X$
the geodesic ray starting at y toward
$c_{y}^{\xi }:[0,\infty )\to X$
the geodesic ray starting at y toward
![]() $\xi \in \partial _{\infty } X$
, then
$\xi \in \partial _{\infty } X$
, then
![]() $p_k$
is written as
$p_k$
is written as
![]() $p_k=c_{g_kx}^{\xi _k}(z_k)$
for some
$p_k=c_{g_kx}^{\xi _k}(z_k)$
for some
![]() $\xi _k\in \partial \mathrm {st}(\tau )$
and
$\xi _k\in \partial \mathrm {st}(\tau )$
and
![]() $z_k>0$
. Since the geodesic ray
$z_k>0$
. Since the geodesic ray
![]() $c_{\bar r(u_k)}^{\xi _k}$
is contained in
$c_{\bar r(u_k)}^{\xi _k}$
is contained in
![]() $V(\bar r(u_k),\partial \mathrm {st}(\tau ))=\partial V(\bar r(u_k), \mathrm {st}(\tau ))$
and
$V(\bar r(u_k),\partial \mathrm {st}(\tau ))=\partial V(\bar r(u_k), \mathrm {st}(\tau ))$
and
![]() $d_X(c_{g_kx}^{\xi _k}(z),c_{\bar r(u_k)}^{\xi _k}(z)) \leq d_X(g_kx,\bar r (u_k))\leq D+R$
for all
$d_X(c_{g_kx}^{\xi _k}(z),c_{\bar r(u_k)}^{\xi _k}(z)) \leq d_X(g_kx,\bar r (u_k))\leq D+R$
for all
![]() $z>0$
,
$z>0$
,
 $$ \begin{align*} l_2+2(D+R) & \leq d_X(\bar r(u_{k+1}), \partial V(\bar r(u_{k}), \mathrm{st}(\tau))) \\ & \leq d_X(\bar r(u_{k+1}), c_{\bar r(u_k)}^{\xi_k}(z_k)) \\ & \leq d_X(\bar r(u_{k+1}), g_{k+1}x)+d_X(g_{k+1}x, c_{g_kx}^{\xi_k}(z_k)) +d_X(c_{g_kx}^{\xi_k}(z_k),c_{\bar r(u_k)}^{\xi_k}(z_k)) \\ & \leq 2(D+R)+d_X(g_{k+1} x, \partial V(g_k x, \mathrm{st}(\tau))), \end{align*} $$
$$ \begin{align*} l_2+2(D+R) & \leq d_X(\bar r(u_{k+1}), \partial V(\bar r(u_{k}), \mathrm{st}(\tau))) \\ & \leq d_X(\bar r(u_{k+1}), c_{\bar r(u_k)}^{\xi_k}(z_k)) \\ & \leq d_X(\bar r(u_{k+1}), g_{k+1}x)+d_X(g_{k+1}x, c_{g_kx}^{\xi_k}(z_k)) +d_X(c_{g_kx}^{\xi_k}(z_k),c_{\bar r(u_k)}^{\xi_k}(z_k)) \\ & \leq 2(D+R)+d_X(g_{k+1} x, \partial V(g_k x, \mathrm{st}(\tau))), \end{align*} $$
which is equivalent to
![]() $ d_X(g_k^{-1}g_{k+1}x, \partial V(x, \mathrm {st}(g_k^{-1}\tau )))=d_X(g_{k+1}x, \partial V(g_k x, \mathrm {st}(\tau )))>l_2$
. Recalling that
$ d_X(g_k^{-1}g_{k+1}x, \partial V(x, \mathrm {st}(g_k^{-1}\tau )))=d_X(g_{k+1}x, \partial V(g_k x, \mathrm {st}(\tau )))>l_2$
. Recalling that
![]() $d_X(g_k^{-1}g_{k+1}x, V(x, \mathrm {st}(g_k^{-1}\tau )))=d_X(g_{k+1}x, V(g_k x, \mathrm {st}(\tau )))<2(D+R)$
, the definition of
$d_X(g_k^{-1}g_{k+1}x, V(x, \mathrm {st}(g_k^{-1}\tau )))=d_X(g_{k+1}x, V(g_k x, \mathrm {st}(\tau )))<2(D+R)$
, the definition of
![]() $l_2$
leads us to conclude that
$l_2$
leads us to conclude that
![]() $\mathcal E((g_{k}^{-1}g_{k+1})^{-1}, g_k^{-1}\tau )>2\lambda $
for all integers
$\mathcal E((g_{k}^{-1}g_{k+1})^{-1}, g_k^{-1}\tau )>2\lambda $
for all integers
![]() $k\geq 0$
. This completes the proof of the lemma.
$k\geq 0$
. This completes the proof of the lemma.
Now, we are ready to finish the proof of Theorem 5.1. By Lemma 5.12, we can define a sequence
![]() $\gamma : \mathbb {N}_0 \to \mathcal {I}_{\eta }$
so that for every
$\gamma : \mathbb {N}_0 \to \mathcal {I}_{\eta }$
so that for every
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $s_{\gamma (k)}=h_k \in \varSigma _{\eta }$
and
$s_{\gamma (k)}=h_k \in \varSigma _{\eta }$
and
![]() $\mathcal E(s_{\gamma (k)}^{-1}, s_{\gamma (k-1)}^{-1}\cdots s_{\gamma (0)}^{-1}\tau )=\mathcal E(h_k^{-1}, h_{k-1}^{-1}\cdots h_0^{-1}\tau )>2\lambda $
, that is,
$\mathcal E(s_{\gamma (k)}^{-1}, s_{\gamma (k-1)}^{-1}\cdots s_{\gamma (0)}^{-1}\tau )=\mathcal E(h_k^{-1}, h_{k-1}^{-1}\cdots h_0^{-1}\tau )>2\lambda $
, that is,
![]() $s_{\gamma (k-1)}^{-1}\cdots s_{\gamma (0)}^{-1}\tau \in U^{2\lambda }_{s_{\gamma (k)}}$
. By equation (5.9), it holds that
$s_{\gamma (k-1)}^{-1}\cdots s_{\gamma (0)}^{-1}\tau \in U^{2\lambda }_{s_{\gamma (k)}}$
. By equation (5.9), it holds that
for every
![]() $k\in \mathbb {N}_0$
, and therefore
$k\in \mathbb {N}_0$
, and therefore
![]() $\gamma $
is a
$\gamma $
is a
![]() $(\mathcal {D}_{\eta },\delta _{\eta })$
-code for
$(\mathcal {D}_{\eta },\delta _{\eta })$
-code for
![]() $\tau $
. Furthermore,
$\tau $
. Furthermore,
for any integer
![]() $k\geq 0$
. Since
$k\geq 0$
. Since
![]() $\{c^{\gamma }(k)=g_{k+1} \mid k\in \mathbb {N}_0\}$
has infinitely many elements of both
$\{c^{\gamma }(k)=g_{k+1} \mid k\in \mathbb {N}_0\}$
has infinitely many elements of both
![]() $c^{\alpha }(\mathbb {N}_0)$
and
$c^{\alpha }(\mathbb {N}_0)$
and
![]() $c^{\beta }(\mathbb {N}_0)$
, we finally conclude that
$c^{\beta }(\mathbb {N}_0)$
, we finally conclude that
![]() $c^{\alpha }\approx ^0_{(\mathcal {D}_{\eta },\delta _{\eta })} c^{\gamma }\approx ^0_{(\mathcal {D}_{\eta },\delta _{\eta })} c^{\beta }$
and thus complete the proof.
$c^{\alpha }\approx ^0_{(\mathcal {D}_{\eta },\delta _{\eta })} c^{\gamma }\approx ^0_{(\mathcal {D}_{\eta },\delta _{\eta })} c^{\beta }$
and thus complete the proof.
6 Actions of word-hyperbolic groups
In this section, we first prove that expansion implies uniform S-hyperbolicity for certain nice actions of hyperbolic groups (Theorem 6.2), and then explore to which extent S-hyperbolic actions of hyperbolic groups arise from their actions on Gromov boundaries.
6.1 Expansion implies S-hyperbolicity
In view of Corollary 3.20, any two
![]() $(\mathcal {D},\delta ;N)$
-equivalent rays in a hyperbolic group are
$(\mathcal {D},\delta ;N)$
-equivalent rays in a hyperbolic group are
![]() $(\mathcal {D},\delta ;N')$
-fellow-traveling for some
$(\mathcal {D},\delta ;N')$
-fellow-traveling for some
![]() $N'\ge 1$
, since two quasi-geodesics in a hyperbolic space X which are Hausdorff-close on unbounded subsets define the same point in
$N'\ge 1$
, since two quasi-geodesics in a hyperbolic space X which are Hausdorff-close on unbounded subsets define the same point in
![]() $\partial _{\infty } X$
. Thus, the meandering hyperbolicity condition enables us to define the following map when
$\partial _{\infty } X$
. Thus, the meandering hyperbolicity condition enables us to define the following map when
![]() $\Gamma $
is a hyperbolic group:
$\Gamma $
is a hyperbolic group:
Definition 6.1 (Postal map)
Let
![]() $\Gamma $
be a hyperbolic group and
$\Gamma $
be a hyperbolic group and
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
meandering-hyperbolic at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
meandering-hyperbolic at
![]() $\Lambda $
with a datum
$\Lambda $
with a datum
![]() $(\mathcal {D}_0\prec \mathcal {D};N)$
. Then we define the postal map
$(\mathcal {D}_0\prec \mathcal {D};N)$
. Then we define the postal map
of
![]() $\rho $
as follows: The value
$\rho $
as follows: The value
![]() $\pi (x)$
of
$\pi (x)$
of
![]() $x\in \Lambda $
is the equivalence class in
$x\in \Lambda $
is the equivalence class in
![]() $\partial _{\infty }\Gamma $
(in the sense of Section 2.2) of a ray
$\partial _{\infty }\Gamma $
(in the sense of Section 2.2) of a ray
![]() $c^{\alpha }\in \mathrm {Ray}_x(\mathcal {D}_0,\delta _0)$
. The equivalence class is well defined since any two
$c^{\alpha }\in \mathrm {Ray}_x(\mathcal {D}_0,\delta _0)$
. The equivalence class is well defined since any two
![]() $(\mathcal {D}_0,\delta _0)$
-rays for
$(\mathcal {D}_0,\delta _0)$
-rays for
![]() $x\in \Lambda $
are
$x\in \Lambda $
are
![]() $(\mathcal {D},\delta ;N')$
-fellow-traveling as mentioned above.
$(\mathcal {D},\delta ;N')$
-fellow-traveling as mentioned above.
The map
![]() $\pi $
is clearly equivariant. In Theorem 6.8, we will prove that
$\pi $
is clearly equivariant. In Theorem 6.8, we will prove that
![]() $\pi $
is a continuous surjective map. We note that, as we show later in Corollary 6.11, meandering-hyperbolic actions of a nonelementary hyperbolic group are in fact (uniformly) S-hyperbolic.
$\pi $
is a continuous surjective map. We note that, as we show later in Corollary 6.11, meandering-hyperbolic actions of a nonelementary hyperbolic group are in fact (uniformly) S-hyperbolic.
Theorem 6.2. Let
![]() $\Gamma $
be a nonelementary hyperbolic group. Suppose that an action
$\Gamma $
be a nonelementary hyperbolic group. Suppose that an action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
$\rho :\Gamma \to \mathrm {LHomeo}(M)$
is expanding at
![]() $\Lambda $
and there exists an equivariant continuous nowhere constant map
$\Lambda $
and there exists an equivariant continuous nowhere constant map
![]() $f:\Lambda \to \partial _{\infty }\Gamma $
. Then
$f:\Lambda \to \partial _{\infty }\Gamma $
. Then
![]() $\rho $
is uniformly S-hyperbolic (and thus meandering-hyperbolic) at
$\rho $
is uniformly S-hyperbolic (and thus meandering-hyperbolic) at
![]() $\Lambda $
and f is the postal map of
$\Lambda $
and f is the postal map of
![]() $\rho $
.
$\rho $
.
Proof. Let
![]() $\mathcal {D}=(\varSigma ,\delta )$
be the expansion datum of
$\mathcal {D}=(\varSigma ,\delta )$
be the expansion datum of
![]() $\rho $
(see Definition 3.4). Recall that
$\rho $
(see Definition 3.4). Recall that
![]() $d_{\varSigma }$
denotes the word metric on
$d_{\varSigma }$
denotes the word metric on
![]() $\Gamma $
with respect to
$\Gamma $
with respect to
![]() $\varSigma $
.
$\varSigma $
.
We claim that if
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $\eta \in (0,\delta ]$
then, for every
$\eta \in (0,\delta ]$
then, for every
![]() $\eta $
-code
$\eta $
-code
![]() $\alpha $
for x, the
$\alpha $
for x, the
![]() $\eta $
-ray
$\eta $
-ray
![]() $c^{\alpha }\in \mathrm {Ray}^{\eta }_{\mathcal {D}}(x)$
is a uniform quasi-geodesic ray in
$c^{\alpha }\in \mathrm {Ray}^{\eta }_{\mathcal {D}}(x)$
is a uniform quasi-geodesic ray in
![]() $(\Gamma ,d_{\varSigma })$
asymptotic to
$(\Gamma ,d_{\varSigma })$
asymptotic to
![]() $f(x)$
. To see this, we first note that by Corollary 3.20 the ray
$f(x)$
. To see this, we first note that by Corollary 3.20 the ray
![]() $c^{\alpha }$
is indeed an
$c^{\alpha }$
is indeed an
![]() $(A,C)$
-quasi-geodesic ray with A and C independent of x and
$(A,C)$
-quasi-geodesic ray with A and C independent of x and
![]() $\eta $
.
$\eta $
.
By Theorem 3.21(1), there is a subsequence
![]() $(g_j)$
of
$(g_j)$
of
![]() $(c^{\alpha }_k)$
such that
$(c^{\alpha }_k)$
such that
![]() $(\rho (g_j))$
converges to x on some ball
$(\rho (g_j))$
converges to x on some ball
![]() $B_{\eta /2}(q)\subset \Lambda $
. Since f is nowhere constant, the image
$B_{\eta /2}(q)\subset \Lambda $
. Since f is nowhere constant, the image
![]() $S:=f(B_{\eta /2}(q))\subset \partial _{\infty }\Gamma $
is not a singleton. By the equivariance of f, the subsequence
$S:=f(B_{\eta /2}(q))\subset \partial _{\infty }\Gamma $
is not a singleton. By the equivariance of f, the subsequence
![]() $(g_j)$
converges to
$(g_j)$
converges to
![]() $\xi :=f(x)$
pointwise on S. Moreover, the initial point
$\xi :=f(x)$
pointwise on S. Moreover, the initial point
![]() $c^{\alpha }_0=s_{\alpha (0)}\in \varSigma $
is a generator of
$c^{\alpha }_0=s_{\alpha (0)}\in \varSigma $
is a generator of
![]() $\Gamma $
. Therefore, Lemma 2.9 applies to the ray
$\Gamma $
. Therefore, Lemma 2.9 applies to the ray
![]() $c^{\alpha }$
and we conclude that the image
$c^{\alpha }$
and we conclude that the image
![]() $c^{\alpha }(\mathbb {N}_0)$
is D-Hausdorff close to a geodesic ray
$c^{\alpha }(\mathbb {N}_0)$
is D-Hausdorff close to a geodesic ray
![]() $e\xi $
in
$e\xi $
in
![]() $(\Gamma ,d_{\varSigma })$
, where the constant D depends only on the hyperbolicity constant of
$(\Gamma ,d_{\varSigma })$
, where the constant D depends only on the hyperbolicity constant of
![]() $(\Gamma ,d_{\varSigma })$
and the quasi-isometry constants
$(\Gamma ,d_{\varSigma })$
and the quasi-isometry constants
![]() $(A,C)$
.
$(A,C)$
.
Now, suppose that
![]() $c^{\alpha },c^{\beta }\in \mathrm {Ray}^{\eta }_{\mathcal {D}}(x)$
are rays associated to
$c^{\alpha },c^{\beta }\in \mathrm {Ray}^{\eta }_{\mathcal {D}}(x)$
are rays associated to
![]() $\eta $
-codes
$\eta $
-codes
![]() $\alpha ,\beta $
for
$\alpha ,\beta $
for
![]() $x\in \Lambda $
, respectively. Then the images of
$x\in \Lambda $
, respectively. Then the images of
![]() $c^{\alpha },c^{\beta }$
are within Hausdorff distance D from a geodesic ray
$c^{\alpha },c^{\beta }$
are within Hausdorff distance D from a geodesic ray
![]() $e\xi $
; hence, these images are
$e\xi $
; hence, these images are
![]() $2D$
-Hausdorff close. Therefore, the rays
$2D$
-Hausdorff close. Therefore, the rays
![]() $2D$
-fellow-travel each other. Since
$2D$
-fellow-travel each other. Since
![]() $x\in \Lambda $
is arbitrary, we conclude that the action is uniformly S-hyperbolic with data
$x\in \Lambda $
is arbitrary, we conclude that the action is uniformly S-hyperbolic with data
![]() $(\mathcal {D};N_{\eta })=(\delta ;2D)$
; recall Definitions 3.23 and 3.25.
$(\mathcal {D};N_{\eta })=(\delta ;2D)$
; recall Definitions 3.23 and 3.25.
Corollary 6.3. Let
![]() $\Gamma $
be a nonelementary hyperbolic group. Suppose that the action of
$\Gamma $
be a nonelementary hyperbolic group. Suppose that the action of
![]() $\Gamma $
on its Gromov boundary
$\Gamma $
on its Gromov boundary
![]() $\partial _{\infty }\Gamma $
is expanding with respect to a metric
$\partial _{\infty }\Gamma $
is expanding with respect to a metric
![]() $d_{\infty }$
compatible with the topology. Then this action is uniformly S-hyperbolic.
$d_{\infty }$
compatible with the topology. Then this action is uniformly S-hyperbolic.
Proof. We set
![]() $M=\Lambda =\partial _{\infty }\Gamma $
and
$M=\Lambda =\partial _{\infty }\Gamma $
and
![]() $f=\mathrm {id}:\partial _{\infty }\Gamma \to \partial _{\infty }\Gamma $
in the preceding theorem.
$f=\mathrm {id}:\partial _{\infty }\Gamma \to \partial _{\infty }\Gamma $
in the preceding theorem.
Let
![]() $\Gamma $
be a nonelementary hyperbolic group and
$\Gamma $
be a nonelementary hyperbolic group and
![]() $d_a$
a visual metric on
$d_a$
a visual metric on
![]() $\partial _{\infty }\Gamma $
(Definition 2.7). Coornaert [Reference Coornaert10, Proposition 3.1, Lemma 6.2] showed that the
$\partial _{\infty }\Gamma $
(Definition 2.7). Coornaert [Reference Coornaert10, Proposition 3.1, Lemma 6.2] showed that the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\partial _{\infty }\Gamma , d_a)$
is expanding. Thus, we have:
$(\partial _{\infty }\Gamma , d_a)$
is expanding. Thus, we have:
Corollary 6.4. Let
![]() $\Gamma $
be a nonelementary hyperbolic group with the Gromov boundary
$\Gamma $
be a nonelementary hyperbolic group with the Gromov boundary
![]() $\partial _{\infty }\Gamma $
equipped with a visual metric
$\partial _{\infty }\Gamma $
equipped with a visual metric
![]() $d_a$
. Then the action of
$d_a$
. Then the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $(\partial _{\infty }\Gamma ,d_a)$
is uniformly S-hyperbolic.
$(\partial _{\infty }\Gamma ,d_a)$
is uniformly S-hyperbolic.
6.2 Meandering-hyperbolic actions of word-hyperbolic groups
It is natural to ask to what extent the converse of Corollary 6.4 is true:
Question 6.5. Does every meandering-hyperbolic action
![]() $\Gamma \to \mathrm {LHomeo}(M)$
at
$\Gamma \to \mathrm {LHomeo}(M)$
at
![]() $\Lambda $
come from the action of a hyperbolic group on its Gromov boundary?
$\Lambda $
come from the action of a hyperbolic group on its Gromov boundary?
Assume first that
![]() $\mathrm {card}(\Lambda )\ge 3$
and the action of
$\mathrm {card}(\Lambda )\ge 3$
and the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
in Question 6.5 is a convergence action (see Section 2.1 for definition). Then, in view of the expansion condition, it is also a uniform convergence action; see [Reference Kapovich, Leeb and Porti26, Lemma 3.13] or [Reference Kapovich and Leeb22, Theorem 8.8] for a different argument. If we assume, in addition, that
$\Lambda $
in Question 6.5 is a convergence action (see Section 2.1 for definition). Then, in view of the expansion condition, it is also a uniform convergence action; see [Reference Kapovich, Leeb and Porti26, Lemma 3.13] or [Reference Kapovich and Leeb22, Theorem 8.8] for a different argument. If we assume, in addition, that
![]() $\Lambda $
is perfect (or that
$\Lambda $
is perfect (or that
![]() $\Lambda $
is the limit set of the action of
$\Lambda $
is the limit set of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
; see Theorem 2.4), then
$\Lambda $
; see Theorem 2.4), then
![]() $\Gamma $
is hyperbolic and
$\Gamma $
is hyperbolic and
![]() $\Lambda $
is equivariantly homeomorphic to the Gromov boundary
$\Lambda $
is equivariantly homeomorphic to the Gromov boundary
![]() $\partial _{\infty }\Gamma $
(Theorem 2.10). To summarize:
$\partial _{\infty }\Gamma $
(Theorem 2.10). To summarize:
Proposition 6.6. Suppose an expanding action
![]() $\Gamma \to \mathrm {LHomeo}(M)$
at
$\Gamma \to \mathrm {LHomeo}(M)$
at
![]() $\Lambda $
is a convergence action with limit set
$\Lambda $
is a convergence action with limit set
![]() $\Lambda $
satisfying
$\Lambda $
satisfying
![]() $\mathrm {card}(\Lambda )\ge 3$
. Then
$\mathrm {card}(\Lambda )\ge 3$
. Then
![]() $\Gamma $
is hyperbolic and
$\Gamma $
is hyperbolic and
![]() $\Lambda $
is equivariantly homeomorphic to
$\Lambda $
is equivariantly homeomorphic to
![]() $\partial _{\infty }\Gamma $
.
$\partial _{\infty }\Gamma $
.
Note that we do not even need to assume faithfulness of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
since, by the convergence action assumption, such an action necessarily has finite kernel.
$\Lambda $
since, by the convergence action assumption, such an action necessarily has finite kernel.
As another application of the formalism of convergence group actions we obtain:
Proposition 6.7. Suppose that
![]() $\Gamma $
is hyperbolic,
$\Gamma $
is hyperbolic,
![]() $d_{\infty }$
is a compatible metric on the Gromov boundary
$d_{\infty }$
is a compatible metric on the Gromov boundary
![]() $\partial _{\infty }\Gamma $
, and the
$\partial _{\infty }\Gamma $
, and the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\partial _{\infty }\Gamma ,d_{\infty })$
is expanding. Define the subset
$(\partial _{\infty }\Gamma ,d_{\infty })$
is expanding. Define the subset
![]() $\varSigma _0\subset \varSigma $
of the finite generating set
$\varSigma _0\subset \varSigma $
of the finite generating set
![]() $\varSigma $
, consisting of elements
$\varSigma $
, consisting of elements
![]() $s_{\alpha }$
with nonempty expansion subsets
$s_{\alpha }$
with nonempty expansion subsets
![]() $U_{\alpha }\subset \Lambda $
. Then
$U_{\alpha }\subset \Lambda $
. Then
![]() $\varSigma _0$
generates a finite index subgroup
$\varSigma _0$
generates a finite index subgroup
![]() $\Gamma _0<\Gamma $
.
$\Gamma _0<\Gamma $
.
Proof. The action of
![]() $\Gamma _0$
on
$\Gamma _0$
on
![]() $\partial _{\infty }\Gamma $
is still expanding and convergence; see Remark 2.3. Therefore, as noted above, the action of
$\partial _{\infty }\Gamma $
is still expanding and convergence; see Remark 2.3. Therefore, as noted above, the action of
![]() $\Gamma _0$
on
$\Gamma _0$
on
![]() $T(\partial _{\infty }\Gamma )$
is also cocompact. Since the action of
$T(\partial _{\infty }\Gamma )$
is also cocompact. Since the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $T(\partial _{\infty }\Gamma )$
is properly discontinuous, it follows that
$T(\partial _{\infty }\Gamma )$
is properly discontinuous, it follows that
![]() $\Gamma _0$
has finite index in
$\Gamma _0$
has finite index in
![]() $\Gamma $
.
$\Gamma $
.
Next, assuming hyperbolicity of
![]() $\Gamma $
in Question 6.5, we can relate
$\Gamma $
in Question 6.5, we can relate
![]() $\Lambda $
and
$\Lambda $
and
![]() $\partial _{\infty }\Gamma $
. Recall the relevant definitions from the beginning of Section 2.
$\partial _{\infty }\Gamma $
. Recall the relevant definitions from the beginning of Section 2.
Theorem 6.8. Let
![]() $\Gamma $
be a nonelementary hyperbolic group. If
$\Gamma $
be a nonelementary hyperbolic group. If
![]() $\Gamma \to \mathrm {LHomeo}(M)$
is a meandering-hyperbolic action at
$\Gamma \to \mathrm {LHomeo}(M)$
is a meandering-hyperbolic action at
![]() $\Lambda $
, then the following hold.
$\Lambda $
, then the following hold.
-
(1) The postal map
 $\pi :\Lambda \to \partial _{\infty }\Gamma $
is an equivariant continuous surjective map.
$\pi :\Lambda \to \partial _{\infty }\Gamma $
is an equivariant continuous surjective map. -
(2) For each minimal nonempty closed
 $\Gamma $
-invariant subset
$\Gamma $
-invariant subset
 $\Lambda _{\mu }\subset \Lambda $
, the restriction
$\Lambda _{\mu }\subset \Lambda $
, the restriction
 $\pi _{\mu }:\Lambda _{\mu }\to \partial _{\infty }\Gamma $
of
$\pi _{\mu }:\Lambda _{\mu }\to \partial _{\infty }\Gamma $
of
 $\pi $
to
$\pi $
to
 $\Lambda _{\mu }$
is a surjective quasi-open map.
$\Lambda _{\mu }$
is a surjective quasi-open map. -
(3) Every
 $\Lambda _{\mu }$
as above is perfect.
$\Lambda _{\mu }$
as above is perfect.
Proof. (1) We already noted the map
![]() $\pi $
is equivariant. Continuity of
$\pi $
is equivariant. Continuity of
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
can be seen as in Section 4.6. Namely, if
$\pi :\Lambda \to \partial _{\infty }\Gamma $
can be seen as in Section 4.6. Namely, if
![]() $x,y\in \Lambda $
are close, there exist
$x,y\in \Lambda $
are close, there exist
![]() $\delta $
-codes
$\delta $
-codes
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
for x and y, respectively, such that
$\beta $
for x and y, respectively, such that
![]() $\alpha (k)=\beta (k)$
for all
$\alpha (k)=\beta (k)$
for all
![]() $0\le k\le n$
, where
$0\le k\le n$
, where
![]() $n\in \mathbb {N}$
is sufficiently large. Then
$n\in \mathbb {N}$
is sufficiently large. Then
for all
![]() $0\le k\le n$
. This means
$0\le k\le n$
. This means
![]() $\pi (y)\in V_n(\pi (x))$
for a sufficiently large n (see Section 2.2), hence
$\pi (y)\in V_n(\pi (x))$
for a sufficiently large n (see Section 2.2), hence
![]() $\pi (x)$
and
$\pi (x)$
and
![]() $\pi (y)$
are close.
$\pi (y)$
are close.
Since
![]() $\Lambda $
is compact, the image
$\Lambda $
is compact, the image
![]() $\pi (\Lambda )$
is closed and
$\pi (\Lambda )$
is closed and
![]() $\Gamma $
-invariant. By the minimality of the action of
$\Gamma $
-invariant. By the minimality of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\partial _{\infty }\Gamma $
, we have
$\partial _{\infty }\Gamma $
, we have
![]() $\pi (\Lambda )=\partial _{\infty }\Gamma $
.
$\pi (\Lambda )=\partial _{\infty }\Gamma $
.
(2) Surjectivity of
![]() $\pi _{\mu }$
follows from the minimality of the action of
$\pi _{\mu }$
follows from the minimality of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\partial _{\infty }\Gamma $
as in part (1). We now prove that each
$\partial _{\infty }\Gamma $
as in part (1). We now prove that each
![]() $\pi _{\mu }$
is quasi-open. Since
$\pi _{\mu }$
is quasi-open. Since
![]() $\Lambda _{\mu }$
is compact, it is locally compact; hence, it suffices to prove that for every compact subset
$\Lambda _{\mu }$
is compact, it is locally compact; hence, it suffices to prove that for every compact subset
![]() $K\subset \Lambda _{\mu }$
with nonempty interior, the image
$K\subset \Lambda _{\mu }$
with nonempty interior, the image
![]() $\pi (K)\subset \partial _{\infty }\Gamma $
also has nonempty interior.
$\pi (K)\subset \partial _{\infty }\Gamma $
also has nonempty interior.
In view of the minimality of the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\Lambda _{\mu }$
and compactness of
$\Lambda _{\mu }$
and compactness of
![]() $\Lambda _{\mu }$
, there exists a finite subset
$\Lambda _{\mu }$
, there exists a finite subset
![]() $\{g_1,\ldots ,g_n\}\subset \Gamma $
such that
$\{g_1,\ldots ,g_n\}\subset \Gamma $
such that
By the equivariance of
![]() $\pi $
and surjectivity of
$\pi $
and surjectivity of
![]() $\pi _{\mu }: \Lambda _{\mu }\to \partial _{\infty }\Gamma $
, we also have
$\pi _{\mu }: \Lambda _{\mu }\to \partial _{\infty }\Gamma $
, we also have
Since a finite collection (even a countable collection) of nowhere dense subsets cannot cover
![]() $\partial _{\infty }\Gamma $
, it follows that
$\partial _{\infty }\Gamma $
, it follows that
![]() $\pi (K)$
has nonempty interior.
$\pi (K)$
has nonempty interior.
(3) Suppose that
![]() $\Lambda _{\mu }$
has an isolated point z. Since the action of
$\Lambda _{\mu }$
has an isolated point z. Since the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda _{\mu }$
is minimal, the compact subset
$\Lambda _{\mu }$
is minimal, the compact subset
![]() $\Lambda _{\mu }\subset \Lambda $
consists entirely of isolated points, that is, is finite. Therefore,
$\Lambda _{\mu }\subset \Lambda $
consists entirely of isolated points, that is, is finite. Therefore,
![]() $\pi (\Lambda _{\mu })\subset \partial _{\infty }\Gamma $
is a finite nonempty
$\pi (\Lambda _{\mu })\subset \partial _{\infty }\Gamma $
is a finite nonempty
![]() $\Gamma $
-invariant subset. This contradicts the minimality of the action of
$\Gamma $
-invariant subset. This contradicts the minimality of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\partial _{\infty }\Gamma $
.
$\partial _{\infty }\Gamma $
.
Remark 6.9. For some minimal S-hyperbolic actions of hyperbolic groups
![]() $\Gamma \to \mathrm {LHomeo}(\Lambda )$
, the map
$\Gamma \to \mathrm {LHomeo}(\Lambda )$
, the map
![]() $\pi $
is not open; see Example 7.6.
$\pi $
is not open; see Example 7.6.
Corollary 6.10. Let
![]() $\Gamma $
be a nonelementary hyperbolic group. If
$\Gamma $
be a nonelementary hyperbolic group. If
![]() $\Gamma \to \mathrm {LHomeo}(M)$
is a meandering-hyperbolic action at
$\Gamma \to \mathrm {LHomeo}(M)$
is a meandering-hyperbolic action at
![]() $\Lambda $
, then:
$\Lambda $
, then:
-
(1)
 $\Gamma $
acts on
$\Gamma $
acts on
 $\Lambda $
with finite kernel K.
$\Lambda $
with finite kernel K. -
(2) If
 $(g_i)$
is a sequence in
$(g_i)$
is a sequence in
 $\Gamma $
converging to the identity on
$\Gamma $
converging to the identity on
 $\Lambda $
, then the projection of this sequence to
$\Lambda $
, then the projection of this sequence to
 $\Gamma /K$
is eventually equal to
$\Gamma /K$
is eventually equal to
 $e\in \Gamma /K$
.
$e\in \Gamma /K$
.
Proof. Both statements are immediate consequences of Theorem 6.8(1) and the convergence property for the action of a
![]() $\Gamma $
on
$\Gamma $
on
![]() $\partial _{\infty }\Gamma $
; see Section 2.2.
$\partial _{\infty }\Gamma $
; see Section 2.2.
As another immediate corollary of the theorem and Theorem 6.2, we obtain:
Corollary 6.11. Let
![]() $\Gamma $
be a nonelementary hyperbolic group. Then every meandering-hyperbolic action of
$\Gamma $
be a nonelementary hyperbolic group. Then every meandering-hyperbolic action of
![]() $\Gamma $
is in fact uniformly S-hyperbolic.
$\Gamma $
is in fact uniformly S-hyperbolic.
These are positive results regarding Question 6.5. In Sections 5 and 7; however, we present several examples which show that in general the question has negative answer.
6.3 S-hyperbolicity and stability for Anosov subgroups
Our goal in this section is to characterize Anosov subgroups in terms of the expansion condition on suitable subsets of partial flag manifolds (Theorem 6.12) and show that the corresponding actions are S-hyperbolic. As an application, we give an alternative proof of the stability of Anosov subgroups (Corollary 6.14).
For the sake of simplicity, we shall restrict our attention to the case of nonelementary hyperbolic groups and make use of Corollary 3.20 and Theorems 6.2 and 6.8. Then Lemma 6.13 below says that the condition (d) in Definition 2.13 is also equivalent to the expansion condition (Definition 3.4) at the image of the boundary embedding. Consequently, we obtain the following characterization of Anosov subgroups:
Theorem 6.12. For a nonelementary hyperbolic subgroup
![]() $\Gamma <G$
, the following are equivalent.
$\Gamma <G$
, the following are equivalent.
-
(1)
 $\Gamma $
is nonuniformly
$\Gamma $
is nonuniformly
 ${\tau _{\mathrm {mod}}}$
-Anosov with asymptotic embedding
${\tau _{\mathrm {mod}}}$
-Anosov with asymptotic embedding
 $\psi :\partial _{\infty }\Gamma \to \Lambda _{\Gamma }({\tau _{\mathrm {mod}}})$
.
$\psi :\partial _{\infty }\Gamma \to \Lambda _{\Gamma }({\tau _{\mathrm {mod}}})$
. -
(2)
 $\Gamma $
is
$\Gamma $
is
 ${\tau _{\mathrm {mod}}}$
-boundary embedded with a boundary embedding
${\tau _{\mathrm {mod}}}$
-boundary embedded with a boundary embedding
 $\varphi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})$
and the
$\varphi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})$
and the
 $\Gamma $
-action on
$\Gamma $
-action on
 $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
 $\varphi (\partial _{\infty }\Gamma )$
.
$\varphi (\partial _{\infty }\Gamma )$
. -
(3) There exists a closed
 $\Gamma $
-invariant antipodal subset
$\Gamma $
-invariant antipodal subset
 $\Lambda \subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that the action
$\Lambda \subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
such that the action
 $\Gamma \to \mathrm {LHomeo}(\mathrm {Flag}({\tau _{\mathrm {mod}}}))$
is S-hyperbolic at
$\Gamma \to \mathrm {LHomeo}(\mathrm {Flag}({\tau _{\mathrm {mod}}}))$
is S-hyperbolic at
 $\Lambda $
with injective postal map
$\Lambda $
with injective postal map
 $\pi :\Lambda \to \partial _{\infty }\Gamma $
.
$\pi :\Lambda \to \partial _{\infty }\Gamma $
.
Moreover, the maps
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
in
$\varphi $
in
![]() $\mathrm {(1)}$
and
$\mathrm {(1)}$
and
![]() $\mathrm {(2)}$
coincide, and the map
$\mathrm {(2)}$
coincide, and the map
![]() $\pi $
in
$\pi $
in
![]() $\mathrm {(3)}$
equals
$\mathrm {(3)}$
equals
![]() $\psi ^{-1}$
.
$\psi ^{-1}$
.
Proof. (2
![]() $\Rightarrow $
3) Let
$\Rightarrow $
3) Let
![]() $\Lambda =\varphi (\partial _{\infty }\Gamma )\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
. It is a closed
$\Lambda =\varphi (\partial _{\infty }\Gamma )\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
. It is a closed
![]() $\Gamma $
-invariant antipodal subset such that the action
$\Gamma $
-invariant antipodal subset such that the action
![]() $\Gamma \to \mathrm {LHomeo}(\mathrm {Flag}({\tau _{\mathrm {mod}}});\Lambda )$
is expanding and the equivariant homeomorphism
$\Gamma \to \mathrm {LHomeo}(\mathrm {Flag}({\tau _{\mathrm {mod}}});\Lambda )$
is expanding and the equivariant homeomorphism
![]() $\varphi ^{-1}:\Lambda \to \partial _{\infty }\Gamma $
is nowhere constant. By Theorem 6.2, this action is S-hyperbolic with postal map
$\varphi ^{-1}:\Lambda \to \partial _{\infty }\Gamma $
is nowhere constant. By Theorem 6.2, this action is S-hyperbolic with postal map
![]() $\varphi ^{-1}$
.
$\varphi ^{-1}$
.
(3
![]() $\Rightarrow $
2) By Theorem 6.8(1), the postal map
$\Rightarrow $
2) By Theorem 6.8(1), the postal map
![]() $\pi $
is equivariant, continuous and surjective. Since
$\pi $
is equivariant, continuous and surjective. Since
![]() $\pi $
is assumed to be injective and
$\pi $
is assumed to be injective and
![]() $\Lambda $
is compact,
$\Lambda $
is compact,
![]() $\pi $
is in fact a homeomorphism. Since
$\pi $
is in fact a homeomorphism. Since
![]() $\Lambda $
is antipodal, the inverse
$\Lambda $
is antipodal, the inverse
![]() $\pi ^{-1}:\partial _{\infty }\Gamma \to \Lambda \subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
is a boundary embedding. The
$\pi ^{-1}:\partial _{\infty }\Gamma \to \Lambda \subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
is a boundary embedding. The
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\Lambda $
is S-hyperbolic, in particular, expanding.
$\Lambda $
is S-hyperbolic, in particular, expanding.
(1
![]() $\Leftrightarrow $
2) This equivalence reduces to the lemma below.
$\Leftrightarrow $
2) This equivalence reduces to the lemma below.
Lemma 6.13. Suppose
![]() $\Gamma <G$
is
$\Gamma <G$
is
![]() ${\tau _{\mathrm {mod}}}$
-boundary embedded with a boundary embedding
${\tau _{\mathrm {mod}}}$
-boundary embedded with a boundary embedding
![]() $\varphi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})$
.
$\varphi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})$
.
-
(1) If
 $\Gamma $
is nonuniformly
$\Gamma $
is nonuniformly
 ${\tau _{\mathrm {mod}}}$
-Anosov with the asymptotic embedding
${\tau _{\mathrm {mod}}}$
-Anosov with the asymptotic embedding
 $\varphi $
, then the
$\varphi $
, then the
 $\Gamma $
-action on
$\Gamma $
-action on
 $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
 $\varphi (\partial _{\infty }\Gamma )$
.
$\varphi (\partial _{\infty }\Gamma )$
. -
(2) If
 $\Gamma $
is nonelementary and the
$\Gamma $
is nonelementary and the
 $\Gamma $
-action on
$\Gamma $
-action on
 $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
 $\varphi (\partial _{\infty }\Gamma )$
, then it is nonuniformly
$\varphi (\partial _{\infty }\Gamma )$
, then it is nonuniformly
 ${\tau _{\mathrm {mod}}}$
-Anosov and
${\tau _{\mathrm {mod}}}$
-Anosov and
 $\varphi $
is the asymptotic embedding for
$\varphi $
is the asymptotic embedding for
 $\Gamma $
.
$\Gamma $
.
Proof. (1) This is a special case of [Reference Kapovich, Leeb and Porti26, Equivalence Theorem 1.1]: Every
![]() ${\tau _{\mathrm {mod}}}$
-Anosov subgroup
${\tau _{\mathrm {mod}}}$
-Anosov subgroup
![]() $\Gamma <G$
is expanding at
$\Gamma <G$
is expanding at
![]() $\varphi (\partial _{\infty }\Gamma )$
. To see this directly, rather, note from the condition (d) in Definition 2.13 that for each
$\varphi (\partial _{\infty }\Gamma )$
. To see this directly, rather, note from the condition (d) in Definition 2.13 that for each
![]() $\xi \in \partial _{\infty }\Gamma $
there is an element
$\xi \in \partial _{\infty }\Gamma $
there is an element
![]() $g\in \Gamma $
such that
$g\in \Gamma $
such that
![]() $\mathcal E(g,\psi (\xi ))>1$
. Then Remark 3.6(c) implies the
$\mathcal E(g,\psi (\xi ))>1$
. Then Remark 3.6(c) implies the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
![]() $\varphi (\partial _{\infty }\Gamma )$
.
$\varphi (\partial _{\infty }\Gamma )$
.
(2) Suppose the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
is expanding at
![]() $\varphi (\partial _{\infty }\Gamma )$
with data
$\varphi (\partial _{\infty }\Gamma )$
with data
![]() $\mathcal {D}=(\delta )$
. Since
$\mathcal {D}=(\delta )$
. Since
![]() $\partial _{\infty }\Gamma $
is perfect, Corollary 3.20 applies. Thus, for any
$\partial _{\infty }\Gamma $
is perfect, Corollary 3.20 applies. Thus, for any
![]() $\eta \in (0,\delta ]$
, the rays
$\eta \in (0,\delta ]$
, the rays
![]() $c^{\alpha }$
associated to
$c^{\alpha }$
associated to
![]() $\eta $
-codes
$\eta $
-codes
![]() $\alpha $
for
$\alpha $
for
![]() $\varphi (\xi )\in \varphi (\partial _{\infty }\Gamma )$
are uniform quasi-geodesic rays in
$\varphi (\xi )\in \varphi (\partial _{\infty }\Gamma )$
are uniform quasi-geodesic rays in
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $\xi \in \partial _{\infty }\Gamma $
, and let
$\xi \in \partial _{\infty }\Gamma $
, and let
![]() $r:\mathbb {N}_0\to \Gamma $
be a geodesic ray starting at
$r:\mathbb {N}_0\to \Gamma $
be a geodesic ray starting at
![]() $e\in \Gamma $
and asymptotic to
$e\in \Gamma $
and asymptotic to
![]() $\xi $
. If
$\xi $
. If
![]() $\alpha $
is an
$\alpha $
is an
![]() $\eta $
-code for
$\eta $
-code for
![]() $\varphi (\xi )$
, then, as in the proof of Lemma 2.9, the Hausdorff distance between
$\varphi (\xi )$
, then, as in the proof of Lemma 2.9, the Hausdorff distance between
![]() $\{r(k)\}_{k\in \mathbb {N}_0}$
and
$\{r(k)\}_{k\in \mathbb {N}_0}$
and
![]() $\{c^{\alpha }_j\}_{j\in \mathbb {N}_0}$
is bounded above by a uniform constant
$\{c^{\alpha }_j\}_{j\in \mathbb {N}_0}$
is bounded above by a uniform constant
![]() $C>0$
. This means that, for each
$C>0$
. This means that, for each
![]() $k\in \mathbb {N}_0$
, there exist
$k\in \mathbb {N}_0$
, there exist
![]() $n_k\in \mathbb {N}_0$
and an element
$n_k\in \mathbb {N}_0$
and an element
![]() $g_k\in \Gamma $
with
$g_k\in \Gamma $
with
![]() $|g_k|_{\varSigma }\le C$
such that
$|g_k|_{\varSigma }\le C$
such that
![]() $r(k)=c^{\alpha }_{n_k} g_k$
. Then we have
$r(k)=c^{\alpha }_{n_k} g_k$
. Then we have
where
![]() $A=\inf \{\mathcal E(g,\varphi (\zeta )) \mid \zeta \in \partial _{\infty }\Gamma ,\ g\in \Gamma \ \mathrm {and} \ |g|_{\varSigma }\le C\}$
. Since
$A=\inf \{\mathcal E(g,\varphi (\zeta )) \mid \zeta \in \partial _{\infty }\Gamma ,\ g\in \Gamma \ \mathrm {and} \ |g|_{\varSigma }\le C\}$
. Since
![]() $\mathcal E( (c^{\alpha }_{j})^{-1},\varphi (\xi ))$
tends to infinity as j tends to infinity (by the last statement of Lemma 3.14), it follows that
$\mathcal E( (c^{\alpha }_{j})^{-1},\varphi (\xi ))$
tends to infinity as j tends to infinity (by the last statement of Lemma 3.14), it follows that
Therefore, the
![]() $\Gamma $
-action satisfies the condition (d) of Definition 2.13.
$\Gamma $
-action satisfies the condition (d) of Definition 2.13.
A corollary of this theorem is the stability of Anosov subgroups; see, for example, [Reference Guichard and Wienhard19, Theorem 1.2] and [Reference Kapovich, Leeb and Porti24, Theorem 1.10]. Let us denote by
the space of faithful representations
![]() $\Gamma \to G$
with (nonuniformly)
$\Gamma \to G$
with (nonuniformly)
![]() ${\tau _{\mathrm {mod}}}$
-Anosov images.
${\tau _{\mathrm {mod}}}$
-Anosov images.
Corollary 6.14. Suppose that
![]() $\Gamma $
is a nonelementary hyperbolic group. Then
$\Gamma $
is a nonelementary hyperbolic group. Then
-
(1)
 $\mathrm {Hom}^{\tau }(\Gamma ,G)$
is open in
$\mathrm {Hom}^{\tau }(\Gamma ,G)$
is open in
 $\mathrm {Hom}(\Gamma ,G)$
.
$\mathrm {Hom}(\Gamma ,G)$
. -
(2) For any sequence of representations
 $\rho _i\in \mathrm {Hom}^{\tau }(\Gamma ,G)$
converging to
$\rho _i\in \mathrm {Hom}^{\tau }(\Gamma ,G)$
converging to
 $\rho \in \mathrm {Hom}^{\tau }(\Gamma ,G)$
, the asymptotic embeddings
$\rho \in \mathrm {Hom}^{\tau }(\Gamma ,G)$
, the asymptotic embeddings
 $\psi _i:\partial _{\infty }\Gamma \to \Lambda _{\rho _i(\Gamma )}({\tau _{\mathrm {mod}}})$
converge uniformly to the asymptotic embedding
$\psi _i:\partial _{\infty }\Gamma \to \Lambda _{\rho _i(\Gamma )}({\tau _{\mathrm {mod}}})$
converge uniformly to the asymptotic embedding
 $\psi :\partial _{\infty }\Gamma \to \Lambda _{\rho (\Gamma )}({\tau _{\mathrm {mod}}})$
.
$\psi :\partial _{\infty }\Gamma \to \Lambda _{\rho (\Gamma )}({\tau _{\mathrm {mod}}})$
.
Proof. We start with an embedding
![]() $\rho \in \mathrm {Hom}^{\tau }(\Gamma ,G)$
; let
$\rho \in \mathrm {Hom}^{\tau }(\Gamma ,G)$
; let
![]() $\Lambda :=\Lambda _{\rho (\Gamma )}({\tau _{\mathrm {mod}}})$
and
$\Lambda :=\Lambda _{\rho (\Gamma )}({\tau _{\mathrm {mod}}})$
and
denote the asymptotic embedding of
![]() $\rho $
. By Theorem 6.12, the
$\rho $
. By Theorem 6.12, the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\Lambda $
is S-hyperbolic. By Theorem 4.4, there exists a small neighborhood
$\Lambda $
is S-hyperbolic. By Theorem 4.4, there exists a small neighborhood
![]() $U'$
of
$U'$
of
![]() $\rho $
in
$\rho $
in
![]() $\mathrm {Hom}(\Gamma ,G)$
such that, for each
$\mathrm {Hom}(\Gamma ,G)$
such that, for each
![]() $\rho '\in U'$
, there exists a
$\rho '\in U'$
, there exists a
![]() $\rho '$
-invariant compact
$\rho '$
-invariant compact
![]() $\Lambda '\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
at which the
$\Lambda '\subset \mathrm {Flag}({\tau _{\mathrm {mod}}})$
at which the
![]() $\rho '$
-action is expanding and there is an equivariant homeomorphism
$\rho '$
-action is expanding and there is an equivariant homeomorphism
![]() $\phi :\Lambda \to \Lambda '$
.
$\phi :\Lambda \to \Lambda '$
.
By Corollary 4.5, for every
![]() $\rho '\in U'$
, the kernel of the action of
$\rho '\in U'$
, the kernel of the action of
![]() $\Gamma '= \rho '(\Gamma )$
on
$\Gamma '= \rho '(\Gamma )$
on
![]() $\Lambda '$
equals the kernel of the action of
$\Lambda '$
equals the kernel of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
. Since
$\Lambda $
. Since
![]() $\Gamma $
is assumed to be nonelementary, it acts on
$\Gamma $
is assumed to be nonelementary, it acts on
![]() $\Lambda $
with finite kernel
$\Lambda $
with finite kernel
![]() $\Phi $
(Corollary 6.10). Therefore, the kernel of
$\Phi $
(Corollary 6.10). Therefore, the kernel of
![]() $\rho '$
is contained in the finite subgroup
$\rho '$
is contained in the finite subgroup
![]() $\Phi < \Gamma $
. As explained in [Reference Kapovich, Leeb and Porti24, proof of Corollary 7.34], rigidity of finite subgroups of Lie groups implies that
$\Phi < \Gamma $
. As explained in [Reference Kapovich, Leeb and Porti24, proof of Corollary 7.34], rigidity of finite subgroups of Lie groups implies that
![]() $U'$
contains a smaller neighborhood U of
$U'$
contains a smaller neighborhood U of
![]() $\rho $
such that every
$\rho $
such that every
![]() $\rho '\in U$
is injective on
$\rho '\in U$
is injective on
![]() $\Phi $
. Therefore, every
$\Phi $
. Therefore, every
![]() $\rho '\in U$
is faithful.
$\rho '\in U$
is faithful.
Since
![]() $\Lambda '$
depends continuously on
$\Lambda '$
depends continuously on
![]() $\rho '$
(see Section 4.8), the antipodality of
$\rho '$
(see Section 4.8), the antipodality of
![]() $\Lambda $
leads to the antipodality of
$\Lambda $
leads to the antipodality of
![]() $\Lambda '$
. (In order to guarantee this, one may further reduce the size of U if necessary.) Thus,
$\Lambda '$
. (In order to guarantee this, one may further reduce the size of U if necessary.) Thus,
![]() $\phi \circ \psi :\partial _{\infty }\Gamma \to \Lambda '$
is a boundary embedding of
$\phi \circ \psi :\partial _{\infty }\Gamma \to \Lambda '$
is a boundary embedding of
![]() $\Gamma '$
. From Lemma 6.13(2), we conclude that
$\Gamma '$
. From Lemma 6.13(2), we conclude that
![]() $\Gamma '<G$
is again (nonuniformly)
$\Gamma '<G$
is again (nonuniformly)
![]() ${\tau _{\mathrm {mod}}}$
-Anosov and the boundary embedding
${\tau _{\mathrm {mod}}}$
-Anosov and the boundary embedding
![]() $\phi \circ \psi $
of
$\phi \circ \psi $
of
![]() $\Gamma '$
is uniformly close to
$\Gamma '$
is uniformly close to
![]() $\psi $
.
$\psi $
.
6.4 Historical remarks on stability
The history of stability for convex-cocompact (and, more generally, geometrically finite) Kleinian groups goes back to the pioneering work of Marden [Reference Marden30] (in the case of subgroups of
![]() $\mathrm {PSL}(2,\mathbb {C})$
). It appears that the first proof of stability of geometrically finite subgroups of
$\mathrm {PSL}(2,\mathbb {C})$
). It appears that the first proof of stability of geometrically finite subgroups of
![]() $\mathrm {Isom}(\mathbb {H}^n)$
(the isometry group of the hyperbolic n-space) was given by Bowditch in [Reference Bowditch5], although many arguments are already contained in [Reference Canary, Epstein and Green8]. Bowditch in his paper also credits this result to P. Tukia. A generalization of the Sullivan’s stability theorem for subgroups of
$\mathrm {Isom}(\mathbb {H}^n)$
(the isometry group of the hyperbolic n-space) was given by Bowditch in [Reference Bowditch5], although many arguments are already contained in [Reference Canary, Epstein and Green8]. Bowditch in his paper also credits this result to P. Tukia. A generalization of the Sullivan’s stability theorem for subgroups of
![]() $\mathrm {Isom}({\mathbb H}^n)$
, proving the existence of a quasi-conformal conjugation on the entire sphere at infinity, was given by Izeki [Reference Izeki20].
$\mathrm {Isom}({\mathbb H}^n)$
, proving the existence of a quasi-conformal conjugation on the entire sphere at infinity, was given by Izeki [Reference Izeki20].
After Sullivan’s paper [Reference Sullivan35], a proof of stability for convex-cocompact subgroups of rank one semisimple Lie groups was given by Corlette [Reference Corlette12]. Corlette’s proof also goes through in the setting of
![]() $C^1$
-stability as it was observed by Yue [Reference Yue38]. Unlike the proofs of Sullivan and Bowditch, however, Corlette’s proof is based on an application of Anosov flows; the same tool is used in the subsequent proofs of stability of Anosov subgroups of higher rank semisimple Lie groups.
$C^1$
-stability as it was observed by Yue [Reference Yue38]. Unlike the proofs of Sullivan and Bowditch, however, Corlette’s proof is based on an application of Anosov flows; the same tool is used in the subsequent proofs of stability of Anosov subgroups of higher rank semisimple Lie groups.
The notion of Anosov subgroups was introduced by Labourie [Reference Labourie28] as a natural analogue of convex-cocompact groups, and the theory was further developed by Guichard and Wienhard [Reference Guichard and Wienhard19] to include all word-hyperbolic groups. Subsequently, Kapovich, Leeb and Porti [Reference Kapovich, Leeb and Porti26] provided new characterizations of Anosov subgroups investigating their properties from many different perspectives. In particular, they gave an alternative proof of stability of Anosov subgroups in [Reference Kapovich, Leeb and Porti24] using coarse-geometric ideas. Recently, Bochi, Potrie and Sambarino [Reference Bochi, Potrie and Sambarino3] provided a purely dynamical proof of the structural stability of Anosov representations.
On the other hand, a notion of convex-cocompactness for discrete subgroups of
![]() $\mathrm {PGL}(n,\mathbb {R})$
was studied by Danciger, Guéritaud and Kassel in [Reference Danciger, Guéritaud and Kassel13, Definition 1.11]. While every Anosov subgroup is word-hyperbolic, convex-cocompact subgroups of
$\mathrm {PGL}(n,\mathbb {R})$
was studied by Danciger, Guéritaud and Kassel in [Reference Danciger, Guéritaud and Kassel13, Definition 1.11]. While every Anosov subgroup is word-hyperbolic, convex-cocompact subgroups of
![]() $\mathrm {PGL}(n,\mathbb {R})$
in their definition are not necessarily word-hyperbolic. Nevertheless, stability in the sense of linear deformations was established for such groups in [Reference Danciger, Guéritaud and Kassel13, Theorem 1.17(D)].
$\mathrm {PGL}(n,\mathbb {R})$
in their definition are not necessarily word-hyperbolic. Nevertheless, stability in the sense of linear deformations was established for such groups in [Reference Danciger, Guéritaud and Kassel13, Theorem 1.17(D)].
7 Other examples
We present a number of examples and nonexamples of S-hyperbolic actions.
7.1 Expanding but not S-hyperbolic actions
In general, even for hyperbolic groups, the expansion condition alone does not imply the S-hyperbolicity condition.
Example 7.1 (Action with infinite kernel)
Suppose that
![]() $\Gamma '$
and
$\Gamma '$
and
![]() $\Gamma $
are nonelementary hyperbolic groups and
$\Gamma $
are nonelementary hyperbolic groups and
![]() $\phi :\Gamma '\to \Gamma $
is an epimorphism with infinite kernel. We equip the Gromov boundary
$\phi :\Gamma '\to \Gamma $
is an epimorphism with infinite kernel. We equip the Gromov boundary
![]() $\Lambda =\partial _{\infty }\Gamma $
with a visual metric. Then the action
$\Lambda =\partial _{\infty }\Gamma $
with a visual metric. Then the action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(\Lambda )$
is expanding (compare Corollary 6.4). Thus, the associated
$\rho :\Gamma \to \mathrm {LHomeo}(\Lambda )$
is expanding (compare Corollary 6.4). Thus, the associated
![]() $\Gamma '$
-action
$\Gamma '$
-action
![]() $\rho \circ \phi :\Gamma '\to \mathrm {LHomeo}(\Lambda )$
is expanding as well. But this action cannot be S-hyperbolic: see Corollary 6.10.
$\rho \circ \phi :\Gamma '\to \mathrm {LHomeo}(\Lambda )$
is expanding as well. But this action cannot be S-hyperbolic: see Corollary 6.10.
Example 7.2 (Nondiscrete action)
Suppose that
![]() $\Gamma $
is a nonelementary hyperbolic group and
$\Gamma $
is a nonelementary hyperbolic group and
![]() $\rho :\Gamma \to G=\mathrm {Isom}(\mathbb {H}^n)$
is a representation with dense image. Then the associated action
$\rho :\Gamma \to G=\mathrm {Isom}(\mathbb {H}^n)$
is a representation with dense image. Then the associated action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(\Lambda )$
on the visual boundary
$\rho :\Gamma \to \mathrm {LHomeo}(\Lambda )$
on the visual boundary
![]() $\Lambda =\partial _{\infty }\mathbb {H}^n$
is expanding due to the density of
$\Lambda =\partial _{\infty }\mathbb {H}^n$
is expanding due to the density of
![]() $\rho (\Gamma )$
in G. But the action
$\rho (\Gamma )$
in G. But the action
![]() $\rho :\Gamma \to \mathrm {LHomeo}(\Lambda )$
cannot be S-hyperbolic. Indeed, by the density of
$\rho :\Gamma \to \mathrm {LHomeo}(\Lambda )$
cannot be S-hyperbolic. Indeed, by the density of
![]() $\rho (\Gamma )$
in G, there is a sequence of distinct elements
$\rho (\Gamma )$
in G, there is a sequence of distinct elements
![]() $g_i\in \Gamma $
such that
$g_i\in \Gamma $
such that
![]() $\rho (g_i)$
converges to the identity element of G. If
$\rho (g_i)$
converges to the identity element of G. If
![]() $\rho $
were S-hyperbolic, then Corollary 6.10 would give a contradiction that the set
$\rho $
were S-hyperbolic, then Corollary 6.10 would give a contradiction that the set
![]() $\{g_i\}$
is finite.
$\{g_i\}$
is finite.
More generally, the same argument works for representations
![]() $\rho :\Gamma \to G$
of nonelementary hyperbolic groups to a semisimple Lie group G with dense images
$\rho :\Gamma \to G$
of nonelementary hyperbolic groups to a semisimple Lie group G with dense images
![]() $\rho (\Gamma )$
. The associated actions
$\rho (\Gamma )$
. The associated actions
![]() $\rho $
of
$\rho $
of
![]() $\Gamma $
on the partial flag manifolds
$\Gamma $
on the partial flag manifolds
![]() $G/P$
are expanding but not S-hyperbolic.
$G/P$
are expanding but not S-hyperbolic.
7.2 S-hyperbolic actions of hyperbolic groups
In addition to the toy examples in Section 3.2, we now give more interesting examples of S-hyperbolic actions of hyperbolic groups. As we proceed, the associated postal maps
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
will be increasingly more complicated.
$\pi :\Lambda \to \partial _{\infty }\Gamma $
will be increasingly more complicated.
Recall that a discrete subgroup
![]() $\Gamma <\mathrm {Isom}(\mathbb {H}^n)$
is convex-cocompact if its limit set
$\Gamma <\mathrm {Isom}(\mathbb {H}^n)$
is convex-cocompact if its limit set
![]() $\Lambda =\Lambda _{\Gamma }\subset S^{n-1}=\partial _{\infty }\mathbb {H}^n$
is not a singleton and
$\Lambda =\Lambda _{\Gamma }\subset S^{n-1}=\partial _{\infty }\mathbb {H}^n$
is not a singleton and
![]() $\Gamma $
acts cocompactly on the closed convex hull of
$\Gamma $
acts cocompactly on the closed convex hull of
![]() $\Lambda $
in
$\Lambda $
in
![]() $\mathbb {H}^n$
. We refer to [Reference Bowditch4] for details on convex-cocompact and, more generally, geometrically finite isometry groups of hyperbolic spaces.
$\mathbb {H}^n$
. We refer to [Reference Bowditch4] for details on convex-cocompact and, more generally, geometrically finite isometry groups of hyperbolic spaces.
Every convex-cocompact (discrete) subgroup
![]() $\Gamma $
of isometries of
$\Gamma $
of isometries of
![]() $\mathbb {H}^n$
(and, more generally, a rank one symmetric space) is S-hyperbolic. More precisely, for
$\mathbb {H}^n$
(and, more generally, a rank one symmetric space) is S-hyperbolic. More precisely, for
![]() $\Lambda =\Lambda _{\Gamma }$
, the action
$\Lambda =\Lambda _{\Gamma }$
, the action
![]() $\Gamma \to \mathrm {LHomeo}(S^{n-1})$
is S-hyperbolic. This can be either proven directly using a Ford fundamental domain (as in [Reference Sullivan35, Theorem I] by considering the conformal ball model of
$\Gamma \to \mathrm {LHomeo}(S^{n-1})$
is S-hyperbolic. This can be either proven directly using a Ford fundamental domain (as in [Reference Sullivan35, Theorem I] by considering the conformal ball model of
![]() $\mathbb {H}^n$
inside
$\mathbb {H}^n$
inside
![]() $\mathbb {R}^n$
) or regarded as a special case of S-hyperbolicity of Anosov subgroups (Theorem 6.12).
$\mathbb {R}^n$
) or regarded as a special case of S-hyperbolicity of Anosov subgroups (Theorem 6.12).
Unlike the convex-cocompact or Anosov examples, the invariant compact set
![]() $\Lambda $
is not equivariantly homeomorphic to the Gromov boundary in the examples below.
$\Lambda $
is not equivariantly homeomorphic to the Gromov boundary in the examples below.
Example 7.3 (k-fold nontrivial covering)
Let
![]() $S_g$
be a closed oriented hyperbolic surface of genus
$S_g$
be a closed oriented hyperbolic surface of genus
![]() $g\ge 2$
; it is isometric to the quotient
$g\ge 2$
; it is isometric to the quotient
![]() $\mathbb {H}^2/\Gamma $
, where
$\mathbb {H}^2/\Gamma $
, where
![]() $\Gamma \cong \pi _1(S_g)$
is a discrete subgroup of
$\Gamma \cong \pi _1(S_g)$
is a discrete subgroup of
![]() $\mathrm {PSL}(2,\mathbb {R})$
. Take any
$\mathrm {PSL}(2,\mathbb {R})$
. Take any
![]() $k\ge 2$
dividing
$k\ge 2$
dividing
![]() $2g-2$
. Since the Euler number of the unit circle bundle of
$2g-2$
. Since the Euler number of the unit circle bundle of
![]() $S_g$
is
$S_g$
is
![]() $2-2g$
, the same as the Euler number of the action of
$2-2g$
, the same as the Euler number of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $S^1=\partial _{\infty }\mathbb {H}^2$
, it follows that the action of
$S^1=\partial _{\infty }\mathbb {H}^2$
, it follows that the action of
![]() $\Gamma $
lifts to a smooth action
$\Gamma $
lifts to a smooth action
with respect to the degree k covering
![]() $p:\Lambda = S^1\to S^1$
. We pull back the Riemannian metric from the range to the domain
$p:\Lambda = S^1\to S^1$
. We pull back the Riemannian metric from the range to the domain
![]() $\Lambda $
via the map p. Since
$\Lambda $
via the map p. Since
![]() $\Gamma <\mathrm {PSL}(2,\mathbb {R})$
is convex-cocompact, its action on
$\Gamma <\mathrm {PSL}(2,\mathbb {R})$
is convex-cocompact, its action on
![]() $\partial _{\infty } \mathbb {H}^2$
is S-hyperbolic. Let
$\partial _{\infty } \mathbb {H}^2$
is S-hyperbolic. Let
![]() $\{U_{\alpha } \mid i\in \mathcal {I}\}$
be a collection of expanding subsets (arcs) in
$\{U_{\alpha } \mid i\in \mathcal {I}\}$
be a collection of expanding subsets (arcs) in
![]() $S^1=\partial _{\infty } \mathbb {H}^2$
corresponding to a generating set
$S^1=\partial _{\infty } \mathbb {H}^2$
corresponding to a generating set
![]() $\varSigma =\{s_i \mid i \in \mathcal {I}\}$
of
$\varSigma =\{s_i \mid i \in \mathcal {I}\}$
of
![]() $\Gamma $
. As in Example 3.9, we lift these arcs to connected components
$\Gamma $
. As in Example 3.9, we lift these arcs to connected components
These will be expanding subsets for the generators
![]() $s_{j_i}=s_j$
(
$s_{j_i}=s_j$
(
![]() $j\in \mathcal {I}$
,
$j\in \mathcal {I}$
,
![]() $i=1,\ldots ,k$
) of
$i=1,\ldots ,k$
) of
![]() $\Gamma $
. The action
$\Gamma $
. The action
![]() $\widetilde \rho $
will be minimal and S-hyperbolic (because the original action of
$\widetilde \rho $
will be minimal and S-hyperbolic (because the original action of
![]() $\Gamma $
is).
$\Gamma $
is).
Thus, we obtain an example of a minimal S-hyperbolic action of a hyperbolic group on a set
![]() $\Lambda $
which is not equivariantly homeomorphic to
$\Lambda $
which is not equivariantly homeomorphic to
![]() $\partial _{\infty }\Gamma $
.
$\partial _{\infty }\Gamma $
.
Similar examples of S-hyperbolic actions on
![]() $S^1$
can be obtained by starting with a general convex-cocompact Fuchsian subgroup
$S^1$
can be obtained by starting with a general convex-cocompact Fuchsian subgroup
![]() $\Gamma _0< \mathrm {PSL}(2,\mathbb {R})$
and lifting it to an action of a finite central extension
$\Gamma _0< \mathrm {PSL}(2,\mathbb {R})$
and lifting it to an action of a finite central extension
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Gamma _0$
on
$\Gamma _0$
on
![]() $S^1$
via a finite covering
$S^1$
via a finite covering
![]() $S^1\to S^1$
. We refer to the paper [Reference Deroin14] of Deroin for details as well as the related classification of expanding real-analytic group actions on the circle.
$S^1\to S^1$
. We refer to the paper [Reference Deroin14] of Deroin for details as well as the related classification of expanding real-analytic group actions on the circle.
Below is a variation of the above construction.
Example 7.4 (Trivial covering)
Let
![]() $\Gamma _0$
be a nonelementary hyperbolic group with the Gromov boundary
$\Gamma _0$
be a nonelementary hyperbolic group with the Gromov boundary
![]() $\Lambda _0=\partial _{\infty }\Gamma _0$
equipped with a visual metric. Let
$\Lambda _0=\partial _{\infty }\Gamma _0$
equipped with a visual metric. Let
![]() $\Lambda =\Lambda _0\times \{0,1\}$
and
$\Lambda =\Lambda _0\times \{0,1\}$
and
![]() $\Gamma _0\to \mathrm {LHomeo}(\Lambda )$
be the product action where
$\Gamma _0\to \mathrm {LHomeo}(\Lambda )$
be the product action where
![]() $\Gamma _0$
acts trivially on
$\Gamma _0$
acts trivially on
![]() $\{0, 1\}$
. This action is S-hyperbolic but, obviously, nonminimal.
$\{0, 1\}$
. This action is S-hyperbolic but, obviously, nonminimal.
We extend this action of
![]() $\Gamma _0$
to an action of
$\Gamma _0$
to an action of
![]() $\Gamma =\Gamma _0\times \mathbb {Z}_2$
, where the generator of
$\Gamma =\Gamma _0\times \mathbb {Z}_2$
, where the generator of
![]() $\mathbb {Z}_2$
acts by the map
$\mathbb {Z}_2$
acts by the map
with an empty expansion subset. The action
![]() $\Gamma \to \mathrm {LHomeo}(\Lambda )$
is easily seen to be faithful, S-hyperbolic and minimal. It is clear, however, that
$\Gamma \to \mathrm {LHomeo}(\Lambda )$
is easily seen to be faithful, S-hyperbolic and minimal. It is clear, however, that
![]() $\Lambda $
is not equivariantly homeomorphic to
$\Lambda $
is not equivariantly homeomorphic to
![]() $\partial _{\infty }\Gamma \cong \partial _{\infty }\Gamma _0$
.
$\partial _{\infty }\Gamma \cong \partial _{\infty }\Gamma _0$
.
In the preceding examples, we had an equivariant finite covering map
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
. In the next example, the postal map
$\pi :\Lambda \to \partial _{\infty }\Gamma $
. In the next example, the postal map
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
is a finite-to-one open map but not a local homeomorphism; one can regard the map
$\pi :\Lambda \to \partial _{\infty }\Gamma $
is a finite-to-one open map but not a local homeomorphism; one can regard the map
![]() $\pi $
as a generalized branched covering (in the sense that it is an open finite-to-one map which is a covering map away from a codimension
$\pi $
as a generalized branched covering (in the sense that it is an open finite-to-one map which is a covering map away from a codimension
![]() $2$
subset).
$2$
subset).
Example 7.5 (Generalized branched covering)
Let
![]() $\Gamma <\mathrm {PSL}(2,\mathbb {R})$
be a Schottky subgroup, that is, a convex-cocompact nonelementary free subgroup. Its limit set
$\Gamma <\mathrm {PSL}(2,\mathbb {R})$
be a Schottky subgroup, that is, a convex-cocompact nonelementary free subgroup. Its limit set
![]() $\Lambda _{\Gamma }\subset S^1$
is homeomorphic to the Cantor set; it is also equivariantly homeomorphic to the Gromov boundary
$\Lambda _{\Gamma }\subset S^1$
is homeomorphic to the Cantor set; it is also equivariantly homeomorphic to the Gromov boundary
![]() $\partial _{\infty }\Gamma $
.
$\partial _{\infty }\Gamma $
.
We regard
![]() $\Gamma $
as a subgroup of
$\Gamma $
as a subgroup of
![]() $\mathrm {PSL}(2,\mathbb {C})$
via the standard embedding
$\mathrm {PSL}(2,\mathbb {C})$
via the standard embedding
![]() $\mathrm {PSL}(2,\mathbb {R})\to \mathrm {PSL}(2,\mathbb {C})$
. The domain of discontinuity of the action of
$\mathrm {PSL}(2,\mathbb {R})\to \mathrm {PSL}(2,\mathbb {C})$
. The domain of discontinuity of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $S^2$
is
$S^2$
is
![]() $\Omega _{\Gamma }= S^2-\Lambda _{\Gamma }$
; the quotient surface
$\Omega _{\Gamma }= S^2-\Lambda _{\Gamma }$
; the quotient surface
![]() $S=\Omega _{\Gamma }/\Gamma $
is compact and its genus equals to the rank r of
$S=\Omega _{\Gamma }/\Gamma $
is compact and its genus equals to the rank r of
![]() $\Gamma $
. We let
$\Gamma $
. We let
![]() $\chi :\pi _1(S)\to F$
be a homomorphism to a finite group F which is nontrivial on the image of
$\chi :\pi _1(S)\to F$
be a homomorphism to a finite group F which is nontrivial on the image of
![]() $\pi _1(\Omega _{\Gamma })$
in
$\pi _1(\Omega _{\Gamma })$
in
![]() $\pi _1(S)$
. For concreteness, we take the following homomorphism
$\pi _1(S)$
. For concreteness, we take the following homomorphism
![]() $\chi : \pi _1(S)\to F=\mathbb {Z}_2$
. We let
$\chi : \pi _1(S)\to F=\mathbb {Z}_2$
. We let
![]() $\{a_1,b_1,\ldots ,a_r,b_r\}$
denote a generating set of
$\{a_1,b_1,\ldots ,a_r,b_r\}$
denote a generating set of
![]() $\pi _1(S)$
such that
$\pi _1(S)$
such that
![]() $a_1,\ldots ,a_r$
lie in the kernel of the natural homomorphism
$a_1,\ldots ,a_r$
lie in the kernel of the natural homomorphism
![]() $\phi :\pi _1(S)\to \Gamma $
, while
$\phi :\pi _1(S)\to \Gamma $
, while
![]() $\phi $
sends
$\phi $
sends
![]() $b_1,\ldots ,b_r$
to (free) generators of
$b_1,\ldots ,b_r$
to (free) generators of
![]() $\Gamma $
. Then take
$\Gamma $
. Then take
![]() $\chi $
such that
$\chi $
such that
![]() $\chi (a_1)=1\in \mathbb {Z}_2$
, while
$\chi (a_1)=1\in \mathbb {Z}_2$
, while
![]() $\chi $
sends the rest of the generators to
$\chi $
sends the rest of the generators to
![]() $0\in \mathbb {Z}_2$
. This homomorphism to F, therefore, lifts to an epimorphism
$0\in \mathbb {Z}_2$
. This homomorphism to F, therefore, lifts to an epimorphism
![]() $\widetilde \chi :\pi _1(\Omega _{\Gamma })\to F$
with
$\widetilde \chi :\pi _1(\Omega _{\Gamma })\to F$
with
![]() $\Gamma $
-invariant kernel
$\Gamma $
-invariant kernel
![]() $K< \pi _1(\Omega _{\Gamma })$
. Hence, there exists a nontrivial 2-fold covering
$K< \pi _1(\Omega _{\Gamma })$
. Hence, there exists a nontrivial 2-fold covering
associated to K and the action of the group
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Omega _{\Gamma }$
lifts to an action of
$\Omega _{\Gamma }$
lifts to an action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\widetilde \Omega $
. One verifies that p is a proper map which induces a surjective but not injective map
$\widetilde \Omega $
. One verifies that p is a proper map which induces a surjective but not injective map
![]() $p_{\infty }: \mathrm {End}(\widetilde \Omega )\to \mathrm {End}(\Omega _{\Gamma })$
between the spaces of ends of the surfaces
$p_{\infty }: \mathrm {End}(\widetilde \Omega )\to \mathrm {End}(\Omega _{\Gamma })$
between the spaces of ends of the surfaces
![]() $\widetilde \Omega $
and
$\widetilde \Omega $
and
![]() $\Omega _{\Gamma }$
. Since p is a 2-fold covering map, the induced map
$\Omega _{\Gamma }$
. Since p is a 2-fold covering map, the induced map
![]() $p_{\infty }$
is at most 2-to-1 (that is, the fibers of
$p_{\infty }$
is at most 2-to-1 (that is, the fibers of
![]() $p_{\infty }$
have cardinality
$p_{\infty }$
have cardinality
![]() $\le 2$
).
$\le 2$
).
We let
![]() $ds^2$
denote the restriction of the standard Riemannian metric on
$ds^2$
denote the restriction of the standard Riemannian metric on
![]() $S^2$
to the domain
$S^2$
to the domain
![]() $\Omega _{\Gamma }$
and let
$\Omega _{\Gamma }$
and let
![]() $\widetilde {ds^2}$
denote the pullback of
$\widetilde {ds^2}$
denote the pullback of
![]() $ds^2$
to
$ds^2$
to
![]() $\widetilde \Omega $
. The Riemannian metric
$\widetilde \Omega $
. The Riemannian metric
![]() $ds^2$
is, of course, incomplete; the Cauchy completion of the associated Riemannian distance function
$ds^2$
is, of course, incomplete; the Cauchy completion of the associated Riemannian distance function
![]() $d_{\Omega _{\Gamma }}$
on
$d_{\Omega _{\Gamma }}$
on
![]() $\Omega _{\Gamma }$
is naturally homeomorphic to
$\Omega _{\Gamma }$
is naturally homeomorphic to
![]() $S^2$
(which is also the end-compactification of
$S^2$
(which is also the end-compactification of
![]() $\Omega _{\Gamma }$
), as a sequence in
$\Omega _{\Gamma }$
), as a sequence in
![]() $\Omega _{\Gamma }$
is Cauchy with respect to the metric
$\Omega _{\Gamma }$
is Cauchy with respect to the metric
![]() $d_{\Omega _{\Gamma }}$
if and only if it converges in
$d_{\Omega _{\Gamma }}$
if and only if it converges in
![]() $S^2$
. (Here, we are using the assumption that
$S^2$
. (Here, we are using the assumption that
![]() $\Lambda _{\Gamma }$
is contained in the circle
$\Lambda _{\Gamma }$
is contained in the circle
![]() $S^1$
.)
$S^1$
.)
We therefore let
![]() $(M,d)$
denote the Cauchy completion of the Riemannian distance function of
$(M,d)$
denote the Cauchy completion of the Riemannian distance function of
![]() $(\widetilde \Omega , \widetilde {ds^2})$
. One verifies that M is compact and is naturally homeomorphic to the end-compactification of
$(\widetilde \Omega , \widetilde {ds^2})$
. One verifies that M is compact and is naturally homeomorphic to the end-compactification of
![]() $\widetilde \Omega $
. In particular, the covering map
$\widetilde \Omega $
. In particular, the covering map
![]() $p:\widetilde \Omega \to \Omega _{\Gamma }$
extends to a continuous open finite-to-one map
$p:\widetilde \Omega \to \Omega _{\Gamma }$
extends to a continuous open finite-to-one map
sending
![]() $\Lambda := M- \widetilde \Omega $
to
$\Lambda := M- \widetilde \Omega $
to
![]() $\Lambda _{\Gamma }$
. The map
$\Lambda _{\Gamma }$
. The map
![]() $p: M\to S^2$
is locally one-to-one on
$p: M\to S^2$
is locally one-to-one on
![]() $\widetilde \Omega $
but fails to be a local homeomorphism at
$\widetilde \Omega $
but fails to be a local homeomorphism at
![]() $\Lambda $
. Since every element of
$\Lambda $
. Since every element of
![]() $\Gamma $
acts as a Lipschitz map to
$\Gamma $
acts as a Lipschitz map to
![]() $(\widetilde \Omega , \widetilde {ds^2})$
, the action of
$(\widetilde \Omega , \widetilde {ds^2})$
, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $(\widetilde \Omega , \widetilde {ds^2})$
extends to an action of
$(\widetilde \Omega , \widetilde {ds^2})$
extends to an action of
![]() $\Gamma $
on M so that every element of
$\Gamma $
on M so that every element of
![]() $\Gamma $
is a Lipschitz map and
$\Gamma $
is a Lipschitz map and
![]() $\Lambda $
is a
$\Lambda $
is a
![]() $\Gamma $
-invariant compact subset of M. The map
$\Gamma $
-invariant compact subset of M. The map
![]() $p: M\to S^2$
is equivariant with respect to the actions of
$p: M\to S^2$
is equivariant with respect to the actions of
![]() $\Gamma $
on M and on
$\Gamma $
on M and on
![]() $S^2$
. Similarly to our covering maps examples, the action
$S^2$
. Similarly to our covering maps examples, the action
![]() $\Gamma \to \mathrm {LHomeo}(M)$
is S-hyperbolic at
$\Gamma \to \mathrm {LHomeo}(M)$
is S-hyperbolic at
![]() $\Lambda $
. The postal map
$\Lambda $
. The postal map
![]() $\pi :\Lambda \to \Lambda _{\Gamma }=\partial _{\infty }\Gamma $
equals the restriction of p to
$\pi :\Lambda \to \Lambda _{\Gamma }=\partial _{\infty }\Gamma $
equals the restriction of p to
![]() $\Lambda $
and, hence, is not a local homeomorphism.
$\Lambda $
and, hence, is not a local homeomorphism.
In the next example, the postal map
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
is not even an open map.
$\pi :\Lambda \to \partial _{\infty }\Gamma $
is not even an open map.
Example 7.6 (Denjoy blowup)
We let
![]() $\Gamma $
be the fundamental group of a closed hyperbolic surface
$\Gamma $
be the fundamental group of a closed hyperbolic surface
![]() $M^2$
. Let
$M^2$
. Let
![]() $c\subset M^2$
be a simple closed geodesic representing the conjugacy class
$c\subset M^2$
be a simple closed geodesic representing the conjugacy class
![]() $[\gamma ]$
in
$[\gamma ]$
in
![]() $\Gamma $
. The Gromov boundary of
$\Gamma $
. The Gromov boundary of
![]() $\Gamma $
is the circle
$\Gamma $
is the circle
![]() $S^1$
. We perform a blowup of
$S^1$
. We perform a blowup of
![]() $S^1$
at the set
$S^1$
at the set
![]() $\Phi \subset S^1$
of fixed points of the elements in the conjugacy class
$\Phi \subset S^1$
of fixed points of the elements in the conjugacy class
![]() $[\gamma ]$
, replacing every fixed point by a pair of points. See Figure 5. The resulting topological space
$[\gamma ]$
, replacing every fixed point by a pair of points. See Figure 5. The resulting topological space
![]() $\Lambda $
is homeomorphic to the Cantor set; the quotient map
$\Lambda $
is homeomorphic to the Cantor set; the quotient map
is 1-to-1 over
![]() $S^1- \Phi $
and is 2-to-1 over
$S^1- \Phi $
and is 2-to-1 over
![]() $\Phi $
. The map q is quasi-open (with
$\Phi $
. The map q is quasi-open (with
![]() $O_q=\Lambda - q^{-1}(\Phi )$
) but not open. (This map is an analogue of the Cantor function
$O_q=\Lambda - q^{-1}(\Phi )$
) but not open. (This map is an analogue of the Cantor function
![]() $f:C\to [0,1]$
mentioned in the beginning of Section 2.) The action of
$f:C\to [0,1]$
mentioned in the beginning of Section 2.) The action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $S^1$
lifts to a continuous action of
$S^1$
lifts to a continuous action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
with every
$\Lambda $
with every
![]() $g\in [\gamma ]$
fixing all the points of the preimage of the fixed-point set of g in
$g\in [\gamma ]$
fixing all the points of the preimage of the fixed-point set of g in
![]() $S^1$
. In particular, the action of
$S^1$
. In particular, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
is minimal. One can metrize
$\Lambda $
is minimal. One can metrize
![]() $\Lambda $
so that the action
$\Lambda $
so that the action
![]() $\Gamma \to \mathrm {LHomeo}(\Lambda )$
is S-hyperbolic with the postal map
$\Gamma \to \mathrm {LHomeo}(\Lambda )$
is S-hyperbolic with the postal map
![]() $\pi :\Lambda \to \partial _{\infty }\Gamma $
being equal to the quotient map
$\pi :\Lambda \to \partial _{\infty }\Gamma $
being equal to the quotient map
![]() $q:\Lambda \to S^1$
.
$q:\Lambda \to S^1$
.

Figure 5 Denjoy blowup.
More generally, one can define a Denjoy blowup for actions of fundamental groups of higher-dimensional compact hyperbolic manifolds. Let
![]() $M^n=\mathbb {H}^n/\Gamma $
be a compact hyperbolic n-manifold containing a compact totally geodesic hypersurface C. Let
$M^n=\mathbb {H}^n/\Gamma $
be a compact hyperbolic n-manifold containing a compact totally geodesic hypersurface C. Let
![]() $A\subset \mathbb {H}^n$
denote the preimage of C in
$A\subset \mathbb {H}^n$
denote the preimage of C in
![]() $\mathbb {H}^n$
. The visual boundary of each component
$\mathbb {H}^n$
. The visual boundary of each component
![]() $A_i$
of A is an
$A_i$
of A is an
![]() $(n-2)$
-dimensional sphere
$(n-2)$
-dimensional sphere
![]() $S_i\subset S^{n-1}=\partial _{\infty } \mathbb {H}^n$
. The blowup
$S_i\subset S^{n-1}=\partial _{\infty } \mathbb {H}^n$
. The blowup
![]() $\Lambda $
of
$\Lambda $
of
![]() $S^{n-1}$
is then performed by replacing each sphere
$S^{n-1}$
is then performed by replacing each sphere
![]() $S_i$
with two copies of this sphere. The result is a compact topological space
$S_i$
with two copies of this sphere. The result is a compact topological space
![]() $\Lambda $
equipped with a quotient map
$\Lambda $
equipped with a quotient map
![]() $q: \Lambda \to S^{n-1}$
such that q is 1-to-1 over every point not in
$q: \Lambda \to S^{n-1}$
such that q is 1-to-1 over every point not in
![]() $S= \cup _i S_i$
and is 2-to-1 over every point in S. Each connected component of
$S= \cup _i S_i$
and is 2-to-1 over every point in S. Each connected component of
![]() $\Lambda $
is either a singleton or is homeomorphic to the
$\Lambda $
is either a singleton or is homeomorphic to the
![]() $(n-2)$
-dimensional Sierpinsky carpet. The action of
$(n-2)$
-dimensional Sierpinsky carpet. The action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $S^{n-1}$
lifts to a continuous action of
$S^{n-1}$
lifts to a continuous action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
which is S-hyperbolic for a suitable choice of a metric on
$\Lambda $
which is S-hyperbolic for a suitable choice of a metric on
![]() $\Lambda $
.
$\Lambda $
.
7.3 S-hyperbolic actions of nonhyperbolic groups
Here, we consider nonhyperbolic groups and examples of their S-hyperbolic actions.
The following example shows that faithfulness of an S-hyperbolic action on M does not imply faithfulness of perturbed actions.
Example 7.7 (Nondiscrete representation)
Suppose that M is the standard compactification of the hyperbolic space
![]() $\mathbb {H}^4$
,
$\mathbb {H}^4$
,
![]() $P=\mathbb {H}^2\subset \mathbb {H}^4$
is a hyperbolic plane, and
$P=\mathbb {H}^2\subset \mathbb {H}^4$
is a hyperbolic plane, and
![]() $\Lambda =S^1\subset S^3=\partial _{\infty }\mathbb {H}^4$
is the ideal boundary of P. We let
$\Lambda =S^1\subset S^3=\partial _{\infty }\mathbb {H}^4$
is the ideal boundary of P. We let
where
![]() $\Gamma _1$
is a hyperbolic surface group and
$\Gamma _1$
is a hyperbolic surface group and
![]() $\Gamma _2\cong \mathbb {Z}$
. We consider a faithful isometric action
$\Gamma _2\cong \mathbb {Z}$
. We consider a faithful isometric action
![]() $\rho $
of
$\rho $
of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbb {H}^4$
, where
$\mathbb {H}^4$
, where
![]() $\Gamma _1$
preserves P and acts on it properly discontinuously and cocompactly, while
$\Gamma _1$
preserves P and acts on it properly discontinuously and cocompactly, while
![]() $\Gamma _2$
acts as a group of elliptic isometries fixing P pointwise. This action admits a conformal extension to M. Since the subgroup
$\Gamma _2$
acts as a group of elliptic isometries fixing P pointwise. This action admits a conformal extension to M. Since the subgroup
![]() $\Gamma _1< \mathrm {Isom}(\mathbb {H}^4)$
is convex-cocompact, it is expanding at its limit set, which is equal to
$\Gamma _1< \mathrm {Isom}(\mathbb {H}^4)$
is convex-cocompact, it is expanding at its limit set, which is equal to
![]() $\Lambda $
. We take
$\Lambda $
. We take
![]() $\varSigma =\varSigma _1\times \{e\}\cup \{e\}\times \{r,r^{-1}\}$
as a symmetric generating set of
$\varSigma =\varSigma _1\times \{e\}\cup \{e\}\times \{r,r^{-1}\}$
as a symmetric generating set of
![]() $\Gamma $
, where
$\Gamma $
, where
![]() $\varSigma _1$
is a finite generating set of
$\varSigma _1$
is a finite generating set of
![]() $\Gamma _1$
(given by its expanding action) and r is a single generator of
$\Gamma _1$
(given by its expanding action) and r is a single generator of
![]() $\Gamma _2$
. The expansion subsets
$\Gamma _2$
. The expansion subsets
![]() $U_r$
,
$U_r$
,
![]() $U_{r^{-1}}$
of r,
$U_{r^{-1}}$
of r,
![]() $r^{-1}$
(as in the definition of an expanding action) are defined to be the empty set. The action
$r^{-1}$
(as in the definition of an expanding action) are defined to be the empty set. The action
![]() $\rho $
on M is uniformly S-hyperbolic: The expansion property is clear; for uniform S-hyperbolicity, we observe that all the rays in
$\rho $
on M is uniformly S-hyperbolic: The expansion property is clear; for uniform S-hyperbolicity, we observe that all the rays in
![]() $\mathrm {Ray}_x(\mathcal {D},\delta )$
for the action of
$\mathrm {Ray}_x(\mathcal {D},\delta )$
for the action of
![]() $\Gamma $
have the form
$\Gamma $
have the form
where
![]() $s\in \varSigma $
and
$s\in \varSigma $
and
![]() $c^{\alpha }$
is a
$c^{\alpha }$
is a
![]() $\delta $
-ray in
$\delta $
-ray in
![]() $\Gamma _1\times \{e\}$
associated to a special code
$\Gamma _1\times \{e\}$
associated to a special code
![]() $\alpha $
for
$\alpha $
for
![]() $x\in \Lambda $
.
$x\in \Lambda $
.
The image
![]() $\rho (r)$
is an infinite order elliptic rotation. Therefore, we can approximate
$\rho (r)$
is an infinite order elliptic rotation. Therefore, we can approximate
![]() $\rho $
by isometric actions
$\rho $
by isometric actions
![]() $\rho _k$
of
$\rho _k$
of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbb {H}^4$
such that
$\mathbb {H}^4$
such that
![]() $\rho _k|_{\Gamma _1}=\rho |_{\Gamma _1}$
, while
$\rho _k|_{\Gamma _1}=\rho |_{\Gamma _1}$
, while
![]() $\rho _k(r)$
is an elliptic transformation of order i fixing P pointwise. In particular, the representations
$\rho _k(r)$
is an elliptic transformation of order i fixing P pointwise. In particular, the representations
![]() $\rho _k$
are not faithful.
$\rho _k$
are not faithful.
In the next two examples, a nonhyperbolic
![]() $\Gamma $
acts faithfully and S-hyperbolically on
$\Gamma $
acts faithfully and S-hyperbolically on
![]() $\Lambda $
.
$\Lambda $
.
Example 7.8 (Actions of product groups)
For
![]() $k=1,2$
, we consider S-hyperbolic actions
$k=1,2$
, we consider S-hyperbolic actions
![]() $\rho _k: \Gamma _k\to \mathrm {LHomeo}(\Lambda _k)$
. Let
$\rho _k: \Gamma _k\to \mathrm {LHomeo}(\Lambda _k)$
. Let
![]() $(\mathcal {I}_k,\mathcal {U}_k,\varSigma _k)$
be the respective expansion datum. Since
$(\mathcal {I}_k,\mathcal {U}_k,\varSigma _k)$
be the respective expansion datum. Since
![]() $\Lambda _k$
’s are nonempty, the groups
$\Lambda _k$
’s are nonempty, the groups
![]() $\Gamma _k$
are infinite. Consider the group
$\Gamma _k$
are infinite. Consider the group
This group is nonhyperbolic since its Cayley graph contains a quasi-flat (the product of complete geodesics in the Cayley graphs of
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
). Let
$\Gamma _2$
). Let
![]() $\mathcal {I}=\mathcal {I}_1\cup \mathcal {I}_2$
, and we equip
$\mathcal {I}=\mathcal {I}_1\cup \mathcal {I}_2$
, and we equip
![]() $\Gamma $
with a symmetric generating set
$\Gamma $
with a symmetric generating set
Define the space
![]() $\Lambda =\Lambda _1\sqcup \Lambda _2$
. The group
$\Lambda =\Lambda _1\sqcup \Lambda _2$
. The group
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\Lambda $
as follows:
$\Lambda $
as follows:
where
![]() $(\gamma _1,\gamma _2)\in \Gamma _1\times \Gamma _2$
. If the actions of
$(\gamma _1,\gamma _2)\in \Gamma _1\times \Gamma _2$
. If the actions of
![]() $\Gamma _i$
on
$\Gamma _i$
on
![]() $\Lambda _i$
are both faithful so is the action of
$\Lambda _i$
are both faithful so is the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
. As a cover
$\Lambda $
. As a cover
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\Lambda $
, we take the union
$\Lambda $
, we take the union
![]() $\mathcal {U}_1\cup \mathcal {U}_2$
of respective covers. We leave it to the reader to verify that the action of
$\mathcal {U}_1\cup \mathcal {U}_2$
of respective covers. We leave it to the reader to verify that the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda $
is S-hyperbolic.
$\Lambda $
is S-hyperbolic.
This example can be modified to a minimal action. Namely, take identical actions
![]() $\rho _1=\rho _2$
of the same group
$\rho _1=\rho _2$
of the same group
![]() $\Gamma _1=\Gamma _2$
and then extend the action of
$\Gamma _1=\Gamma _2$
and then extend the action of
![]() $\Gamma =\Gamma _1\times \Gamma _1$
on
$\Gamma =\Gamma _1\times \Gamma _1$
on
![]() $\Lambda $
to a minimal action of
$\Lambda $
to a minimal action of
![]() $\Gamma \rtimes \mathbb {Z}_2$
as in Example 7.4. Here, the generator of
$\Gamma \rtimes \mathbb {Z}_2$
as in Example 7.4. Here, the generator of
![]() $\mathbb {Z}_2$
swaps the direct factors of
$\mathbb {Z}_2$
swaps the direct factors of
![]() $\Gamma $
.
$\Gamma $
.
Example 7.9 (
 $\mathbb {Z}^n$
acting on
$\mathbb {Z}^n$
acting on
 $P^n(\mathbb {R})$
)
$P^n(\mathbb {R})$
)
There is an S-hyperbolic action of
![]() $\mathbb {Z}^n$
on
$\mathbb {Z}^n$
on
![]() $M=P^n(\mathbb {R})$
by projective transformations.
$M=P^n(\mathbb {R})$
by projective transformations.
Let
![]() $\{E_i\mid i=0,1,\ldots ,n\}$
be the standard basis of
$\{E_i\mid i=0,1,\ldots ,n\}$
be the standard basis of
![]() $\mathbb {R}^{n+1}$
. Let
$\mathbb {R}^{n+1}$
. Let
![]() $\mathbb {Z}^n<\mathrm {GL}(n+1,\mathbb {R})$
be the free abelian group of rank n generated by biproximal diagonal matrices
$\mathbb {Z}^n<\mathrm {GL}(n+1,\mathbb {R})$
be the free abelian group of rank n generated by biproximal diagonal matrices
![]() $G_j$
(
$G_j$
(
![]() $1\le j\le n$
) for which
$1\le j\le n$
) for which
![]() $E_0$
(resp.
$E_0$
(resp.
![]() $E_j$
) is the eigenvector of the biggest (resp. smallest) modulus eigenvalue. Denote by
$E_j$
) is the eigenvector of the biggest (resp. smallest) modulus eigenvalue. Denote by
![]() $e_i\in P^n(\mathbb {R})$
and
$e_i\in P^n(\mathbb {R})$
and
![]() $g_j\in \mathrm {PGL}(n+1,\mathbb {R})$
the projectivizations of
$g_j\in \mathrm {PGL}(n+1,\mathbb {R})$
the projectivizations of
![]() $E_i$
and
$E_i$
and
![]() $G_j$
, respectively. Let
$G_j$
, respectively. Let
![]() $\Lambda =\{e_i\mid i=0,1,\ldots ,n\}\subset P^n(\mathbb {R})=M$
and
$\Lambda =\{e_i\mid i=0,1,\ldots ,n\}\subset P^n(\mathbb {R})=M$
and
![]() $\varSigma =\{g_j,g_j^{-1}\mid 1\le j\le n\}$
. We claim that the action
$\varSigma =\{g_j,g_j^{-1}\mid 1\le j\le n\}$
. We claim that the action
![]() $\mathbb {Z}^n\to \mathrm {LHomeo}(M)$
is S-hyperbolic.
$\mathbb {Z}^n\to \mathrm {LHomeo}(M)$
is S-hyperbolic.
Let
![]() $U_{g_j}\subset M$
denote an expanding subset of
$U_{g_j}\subset M$
denote an expanding subset of
![]() $g_j$
and similarly
$g_j$
and similarly
![]() $U_{g_j^{-1}}$
for
$U_{g_j^{-1}}$
for
![]() $g_j^{-1}$
. We assume that
$g_j^{-1}$
. We assume that
![]() $U_{g_j^{-1}}=\emptyset $
for
$U_{g_j^{-1}}=\emptyset $
for
![]() $j=2,3,\ldots ,n$
but that
$j=2,3,\ldots ,n$
but that
![]() $U_{g_1^{-1}}$
as well as
$U_{g_1^{-1}}$
as well as
![]() $U_{g_j}$
(
$U_{g_j}$
(
![]() $1\le j\le n$
) are nonempty. Then
$1\le j\le n$
) are nonempty. Then
![]() $\mathcal {U}=\{U_{g_j},U_{g_j^{-1}}\mid 1\le j\le n\}$
covers
$\mathcal {U}=\{U_{g_j},U_{g_j^{-1}}\mid 1\le j\le n\}$
covers
![]() $\Lambda $
since
$\Lambda $
since
![]() $e_0\in U_{g_1^{-1}}$
and
$e_0\in U_{g_1^{-1}}$
and
![]() $e_j\in U_{g_j}$
for
$e_j\in U_{g_j}$
for
![]() $1\le j\le n$
. Thus, the action is expanding.
$1\le j\le n$
. Thus, the action is expanding.
A ray associated to
![]() $e_j\in \Lambda $
is of the form
$e_j\in \Lambda $
is of the form
![]() $\left (g(g_j^{-1})^k\right )_{k\in \mathbb {N}_0}$
with
$\left (g(g_j^{-1})^k\right )_{k\in \mathbb {N}_0}$
with
![]() $g\in \varSigma $
and a ray associated to
$g\in \varSigma $
and a ray associated to
![]() $e_0\in \Lambda $
is of the form
$e_0\in \Lambda $
is of the form
![]() $\left (g(g_1)^k\right )_{k\in \mathbb {N}_0}$
with
$\left (g(g_1)^k\right )_{k\in \mathbb {N}_0}$
with
![]() $g\in \varSigma $
. In any case, each point in
$g\in \varSigma $
. In any case, each point in
![]() $\Lambda $
has only a finite number of rays associated to it. Hence, the S-hyperbolicity follows.
$\Lambda $
has only a finite number of rays associated to it. Hence, the S-hyperbolicity follows.
7.4 Embedding into Lie group actions on homogeneous manifolds
Examples 7.3, 7.4 and 7.8 can be embedded in smooth Lie group actions on homogeneous manifolds.
For instance, consider the action of
![]() $\mathrm {GL}(3,\mathbb {R})$
on the space of oriented lines in
$\mathrm {GL}(3,\mathbb {R})$
on the space of oriented lines in
![]() $\mathbb {R}^3$
, which we identify with the 2-sphere
$\mathbb {R}^3$
, which we identify with the 2-sphere
![]() $S^2$
equipped with its standard metric. We have the equivariant 2-fold covering
$S^2$
equipped with its standard metric. We have the equivariant 2-fold covering
![]() $p:S^2\to P^2(\mathbb {R})$
with the covering group generated by the antipodal map
$p:S^2\to P^2(\mathbb {R})$
with the covering group generated by the antipodal map
![]() $-I\in \mathrm {GL}(3,\mathbb {R})$
. Let
$-I\in \mathrm {GL}(3,\mathbb {R})$
. Let
![]() $\mathbb {H}^2\subset P^2(\mathbb {R})$
be the Klein model of the hyperbolic plane invariant under a subgroup
$\mathbb {H}^2\subset P^2(\mathbb {R})$
be the Klein model of the hyperbolic plane invariant under a subgroup
![]() $\mathrm {PSO}(2,1)<\mathrm {PSL}(3,\mathbb {R})$
. Then
$\mathrm {PSO}(2,1)<\mathrm {PSL}(3,\mathbb {R})$
. Then
![]() $p^{-1}(\mathbb {H}^2)$
consists of two disjoint copies of the hyperbolic plane bounded by two circles
$p^{-1}(\mathbb {H}^2)$
consists of two disjoint copies of the hyperbolic plane bounded by two circles
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
. Taking a discrete convex-cocompact subgroup
$\Lambda _2$
. Taking a discrete convex-cocompact subgroup
![]() $\Gamma _1< \mathrm {SO}(2,1)< \mathrm {SL}(3,\mathbb {R})$
,
$\Gamma _1< \mathrm {SO}(2,1)< \mathrm {SL}(3,\mathbb {R})$
,
![]() $\Gamma = \Gamma _1\times \langle -I \rangle \cong \Gamma _1\times \mathbb {Z}_2$
and
$\Gamma = \Gamma _1\times \langle -I \rangle \cong \Gamma _1\times \mathbb {Z}_2$
and
![]() $\Lambda = \Lambda _1\cup \Lambda _2$
, we obtain an S-hyperbolic action
$\Lambda = \Lambda _1\cup \Lambda _2$
, we obtain an S-hyperbolic action
which restricts on
![]() $\Lambda $
to Example 7.4. (When the group
$\Lambda $
to Example 7.4. (When the group
![]() $\Gamma _1$
is free, such an action is studied in detail by Choi and Goldman [Reference Choi and Goldman9]; see also [Reference Stecker and Treib34] for a greater generalization of the Choi–Goldman construction.)
$\Gamma _1$
is free, such an action is studied in detail by Choi and Goldman [Reference Choi and Goldman9]; see also [Reference Stecker and Treib34] for a greater generalization of the Choi–Goldman construction.)
Below is a more general version of the preceding construction. Recall that the set
![]() $\mathrm {Hom}^{\tau }(\Gamma ,G)$
of
$\mathrm {Hom}^{\tau }(\Gamma ,G)$
of
![]() ${\tau _{\mathrm {mod}}}$
-Anosov representations
${\tau _{\mathrm {mod}}}$
-Anosov representations
![]() $\Gamma \to G$
forms an open subset of the representation variety
$\Gamma \to G$
forms an open subset of the representation variety
![]() $\mathrm {Hom}(\Gamma ,G)$
(see Corollary 6.14). Let
$\mathrm {Hom}(\Gamma ,G)$
(see Corollary 6.14). Let
![]() $\Gamma =\pi _1(S_g)$
(
$\Gamma =\pi _1(S_g)$
(
![]() $g\ge 2$
) and
$g\ge 2$
) and
![]() $G=\mathrm {PSL}(n,\mathbb {R})$
(
$G=\mathrm {PSL}(n,\mathbb {R})$
(
![]() $n\ge 3$
). We will consider two types of simplices
$n\ge 3$
). We will consider two types of simplices
![]() ${\tau _{\mathrm {mod}}}$
for the Lie group G:
${\tau _{\mathrm {mod}}}$
for the Lie group G:
-
•
 ${\sigma _{\mathrm {mod}}}$
; the corresponding flag manifold
${\sigma _{\mathrm {mod}}}$
; the corresponding flag manifold
 $\mathrm {Flag}({\sigma _{\mathrm {mod}}})$
consists of full flags in
$\mathrm {Flag}({\sigma _{\mathrm {mod}}})$
consists of full flags in
 $\mathbb {R}^n$
.
$\mathbb {R}^n$
. -
•
 ${\tau _{\mathrm {mod}}}$
of the type ‘pointed hyperplanes’; the corresponding flag manifold
${\tau _{\mathrm {mod}}}$
of the type ‘pointed hyperplanes’; the corresponding flag manifold
 $\mathrm {Flag}({\tau _{\mathrm {mod}}})$
consists of pairs
$\mathrm {Flag}({\tau _{\mathrm {mod}}})$
consists of pairs
 $V_1\subset V_{n-1} \subset \mathbb {R}^n$
of lines contained in hyperplanes in
$V_1\subset V_{n-1} \subset \mathbb {R}^n$
of lines contained in hyperplanes in
 $\mathbb {R}^n$
.
$\mathbb {R}^n$
.
In both cases, we have a natural fibration
![]() $q: \mathrm {Flag}({\tau _{\mathrm {mod}}})\to P(\mathbb {R}^n)$
sending each flag to the line in the flag.
$q: \mathrm {Flag}({\tau _{\mathrm {mod}}})\to P(\mathbb {R}^n)$
sending each flag to the line in the flag.
Example 7.10 (Hitchin and Barbot representations)
The Hitchin representations are
![]() ${\sigma _{\mathrm {mod}}}$
-Anosov representations belonging to a connected component
${\sigma _{\mathrm {mod}}}$
-Anosov representations belonging to a connected component
![]() $\mathrm {Hom}^{\mathrm {Hit}}(\Gamma ,G)$
of
$\mathrm {Hom}^{\mathrm {Hit}}(\Gamma ,G)$
of
![]() $\mathrm {Hom}^{\sigma }(\Gamma ,G)$
containing a representation
$\mathrm {Hom}^{\sigma }(\Gamma ,G)$
containing a representation
where the first map is a Fuchsian representation of
![]() $\Gamma $
and the second an irreducible embedding of
$\Gamma $
and the second an irreducible embedding of
![]() $\mathrm {PSL}(2,\mathbb {R})$
.
$\mathrm {PSL}(2,\mathbb {R})$
.
We may also consider the standard reducible embedding
![]() $\iota :\mathrm {SL}(2,\mathbb {R})\hookrightarrow \mathrm {SL}(n,\mathbb {R})$
given by
$\iota :\mathrm {SL}(2,\mathbb {R})\hookrightarrow \mathrm {SL}(n,\mathbb {R})$
given by
![]() . Let
. Let
![]() $\varphi :\Gamma \hookrightarrow \mathrm {PSL}(2,\mathbb {R})$
be a Fuchsian representation and
$\varphi :\Gamma \hookrightarrow \mathrm {PSL}(2,\mathbb {R})$
be a Fuchsian representation and
![]() $\tilde {\varphi }:\Gamma \hookrightarrow \mathrm {SL}(2,\mathbb {R})$
one of the
$\tilde {\varphi }:\Gamma \hookrightarrow \mathrm {SL}(2,\mathbb {R})$
one of the
![]() $2g$
lifts of
$2g$
lifts of
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $p:\mathrm {SL}(n,\mathbb {R})\to \mathrm {PSL}(n,\mathbb {R})$
denote the covering map, which is of degree
$p:\mathrm {SL}(n,\mathbb {R})\to \mathrm {PSL}(n,\mathbb {R})$
denote the covering map, which is of degree
![]() $2$
if and only if n is even. Representations of the form
$2$
if and only if n is even. Representations of the form
are
![]() ${\tau _{\mathrm {mod}}}$
-Anosov, where
${\tau _{\mathrm {mod}}}$
-Anosov, where
![]() ${\tau _{\mathrm {mod}}}$
has the type of pointed hyperplanes. Let
${\tau _{\mathrm {mod}}}$
has the type of pointed hyperplanes. Let
![]() $\mathrm {Hom}^{\mathrm {Bar}}(\Gamma ,G)$
be the union of connected components of
$\mathrm {Hom}^{\mathrm {Bar}}(\Gamma ,G)$
be the union of connected components of
![]() $\mathrm {Hom}^{\tau }(\Gamma ,G)$
containing such representations. We say representations in
$\mathrm {Hom}^{\tau }(\Gamma ,G)$
containing such representations. We say representations in
![]() $\mathrm {Hom}^{\mathrm {Bar}}(\Gamma ,G)$
are of Barbot type; see [Reference Barbot2] for the case
$\mathrm {Hom}^{\mathrm {Bar}}(\Gamma ,G)$
are of Barbot type; see [Reference Barbot2] for the case
![]() $n=3$
.
$n=3$
.
Let
![]() $\rho :\Gamma \to \mathrm {PSL}(n,\mathbb {R})$
be a Hitchin representation. It is known [Reference Labourie28] that the projection
$\rho :\Gamma \to \mathrm {PSL}(n,\mathbb {R})$
be a Hitchin representation. It is known [Reference Labourie28] that the projection
![]() $q\circ \psi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\sigma _{\mathrm {mod}}})\to P^{n-1}(\mathbb {R})$
of the asymptotic embedding
$q\circ \psi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\sigma _{\mathrm {mod}}})\to P^{n-1}(\mathbb {R})$
of the asymptotic embedding
![]() $\psi $
is a hyperconvex curve. This curve is homotopically trivial if and only if n is odd. On the other hand, if
$\psi $
is a hyperconvex curve. This curve is homotopically trivial if and only if n is odd. On the other hand, if
![]() $\rho $
is of Barbot type, the curve
$\rho $
is of Barbot type, the curve
![]() $q\circ \psi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})\to P^{n-1}(\mathbb {R})$
is always homotopically nontrivial.
$q\circ \psi :\partial _{\infty }\Gamma \to \mathrm {Flag}({\tau _{\mathrm {mod}}})\to P^{n-1}(\mathbb {R})$
is always homotopically nontrivial.
We now lift to the space of oriented full flags (resp. oriented line-hyperplane flags). Accordingly, we lift the action of
![]() $\Gamma $
on the sphere
$\Gamma $
on the sphere
![]() $S^{n-1}$
. The preimage
$S^{n-1}$
. The preimage
![]() $\Lambda $
of
$\Lambda $
of
![]() $(q\circ \psi )(\partial _{\infty }\Gamma )$
in
$(q\circ \psi )(\partial _{\infty }\Gamma )$
in
![]() $S^{n-1}$
is either a Jordan curve or a disjoint union of two Jordan curves, with the 2-fold equivariant covering map
$S^{n-1}$
is either a Jordan curve or a disjoint union of two Jordan curves, with the 2-fold equivariant covering map
The result is an S-hyperbolic action
![]() $\tilde \rho : \Gamma \to \mathrm {Diff}(S^n)$
, where
$\tilde \rho : \Gamma \to \mathrm {Diff}(S^n)$
, where
![]() $\tilde \rho (\Gamma )$
is contained in the image of the group
$\tilde \rho (\Gamma )$
is contained in the image of the group
![]() $\mathrm {SL}(n,\mathbb {R})$
in
$\mathrm {SL}(n,\mathbb {R})$
in
![]() $\mathrm {Diff}(S^n)$
. The restrictions of the
$\mathrm {Diff}(S^n)$
. The restrictions of the
![]() $\Gamma $
-actions to
$\Gamma $
-actions to
![]() $\Lambda $
are as in Example 7.3 (with
$\Lambda $
are as in Example 7.3 (with
![]() $k=2$
) and Example 7.4.
$k=2$
) and Example 7.4.
Example 7.11 (Embedded product examples)
We embed Example 7.8 in the action of
![]() $\mathrm {SL}(4,\mathbb {R})$
on
$\mathrm {SL}(4,\mathbb {R})$
on
![]() $P^3(\mathbb {R})$
. Consider
$P^3(\mathbb {R})$
. Consider
![]() $G_1\times G_2= \mathrm {SL}(2,\mathbb {R})\times \mathrm {SL}(2,\mathbb {R})< G= \mathrm {SL}(4,\mathbb {R})$
. The action of
$G_1\times G_2= \mathrm {SL}(2,\mathbb {R})\times \mathrm {SL}(2,\mathbb {R})< G= \mathrm {SL}(4,\mathbb {R})$
. The action of
![]() $G_1\times G_2$
on
$G_1\times G_2$
on
![]() $\mathbb {R}^4$
is reducible, preserving a direct sum decomposition
$\mathbb {R}^4$
is reducible, preserving a direct sum decomposition
where
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are two-dimensional subspaces and
$V_2$
are two-dimensional subspaces and
![]() $G_i$
acts trivially on
$G_i$
acts trivially on
![]() $V_{3-k}$
for
$V_{3-k}$
for
![]() $k=1,2$
. Let
$k=1,2$
. Let
![]() $\tau $
be an involution of
$\tau $
be an involution of
![]() $\mathbb {R}^4$
swapping
$\mathbb {R}^4$
swapping
![]() $V_1$
and
$V_1$
and
![]() $V_2$
. For
$V_2$
. For
![]() $i=1,2$
, take
$i=1,2$
, take
![]() $\Gamma _k< G_k$
to be an infinite (possibly elementary) convex-cocompact subgroup with the limit set
$\Gamma _k< G_k$
to be an infinite (possibly elementary) convex-cocompact subgroup with the limit set
![]() $\Lambda _k\subset P(V_k)$
. Then the subgroup
$\Lambda _k\subset P(V_k)$
. Then the subgroup
![]() $\Gamma = \Gamma _1 \times \Gamma _2< G$
acts on
$\Gamma = \Gamma _1 \times \Gamma _2< G$
acts on
![]() $P^3(\mathbb {R})$
preserving the union
$P^3(\mathbb {R})$
preserving the union
![]() $\Lambda =\Lambda _1\sqcup \Lambda _2\subset P(V_1)\sqcup P(V_2)$
. We equip
$\Lambda =\Lambda _1\sqcup \Lambda _2\subset P(V_1)\sqcup P(V_2)$
. We equip
![]() $P^3(\mathbb {R})$
with its standard Riemannian metric. The action
$P^3(\mathbb {R})$
with its standard Riemannian metric. The action
is S-hyperbolic and restricts on
![]() $\Lambda $
to Example 7.8. As in Example 7.8, taking
$\Lambda $
to Example 7.8. As in Example 7.8, taking
![]() $\Gamma _1=\Gamma _2$
and an index two extension
$\Gamma _1=\Gamma _2$
and an index two extension
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Gamma _1\times \Gamma _2$
we can extend this action to an S-hyperbolic action minimal on
$\Gamma _1\times \Gamma _2$
we can extend this action to an S-hyperbolic action minimal on
![]() $\Lambda $
using the involution
$\Lambda $
using the involution
![]() $\tau $
.
$\tau $
.
7.5 Algebraically stable but not convex-cocompact
We provide an example to the claim made in Remark 4.7 that for groups with torsion the implication (4
![]() $\Rightarrow $
1) in Sullivan’s paper [Reference Sullivan35] is false.
$\Rightarrow $
1) in Sullivan’s paper [Reference Sullivan35] is false.
Example 7.12 (Quasi-conformally stable nonconvex-cocompact subgroups of
 $\mathrm {PSL}(2,\mathbb {C})$
)
$\mathrm {PSL}(2,\mathbb {C})$
)
We recall also that a von Dyck group
![]() $D(p,q,r)$
is given by the presentation
$D(p,q,r)$
is given by the presentation
Such groups are called hyperbolic (resp. parabolic, elliptic) if the number
is
![]() $<1$
(resp.
$<1$
(resp.
![]() $=1$
,
$=1$
,
![]() $>1$
). Depending on the type
$>1$
). Depending on the type
![]() $D(p,q,r)$
can be embedded (uniquely up to conjugation) as a discrete cocompact subgroup of isometries of hyperbolic plane (if
$D(p,q,r)$
can be embedded (uniquely up to conjugation) as a discrete cocompact subgroup of isometries of hyperbolic plane (if
![]() $\chi <1$
), a discrete cocompact subgroup of the group
$\chi <1$
), a discrete cocompact subgroup of the group
![]() $\mathrm {Aff}({\mathbb {C}})$
of complex affine transformations of
$\mathrm {Aff}({\mathbb {C}})$
of complex affine transformations of
![]() $\mathbb {C}$
(if
$\mathbb {C}$
(if
![]() $\chi =1$
), or is finite and embeds in the group of isometries of the 2-sphere (if
$\chi =1$
), or is finite and embeds in the group of isometries of the 2-sphere (if
![]() $\chi>1$
).
$\chi>1$
).
Let
![]() $\Gamma _k$
(
$\Gamma _k$
(
![]() $k=1,2$
) be two discrete elementary subgroups of
$k=1,2$
) be two discrete elementary subgroups of
![]() $\mathrm {Aff}(\mathbb {C})<\mathrm {PSL}(2,\mathbb {C})$
isomorphic to parabolic von Dyck groups
$\mathrm {Aff}(\mathbb {C})<\mathrm {PSL}(2,\mathbb {C})$
isomorphic to parabolic von Dyck groups
These groups consist of elliptic and parabolic elements and are virtually free abelian of rank 2; hence, they cannot be contained in a convex-cocompact group. Subgroups of
![]() $\mathrm {PSL}(2,\mathbb {C})$
isomorphic to von Dyck groups are (locally) rigid. One can choose embeddings of the groups
$\mathrm {PSL}(2,\mathbb {C})$
isomorphic to von Dyck groups are (locally) rigid. One can choose embeddings of the groups
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
into
$\Gamma _2$
into
![]() $\mathrm {PSL}(2,\mathbb {C})$
such that they generate a free product
$\mathrm {PSL}(2,\mathbb {C})$
such that they generate a free product
which is geometrically finite and every parabolic element of
![]() $\Gamma $
is conjugate into one of the free factors. (The group
$\Gamma $
is conjugate into one of the free factors. (The group
![]() $\Gamma $
is obtained via the Klein combination of
$\Gamma $
is obtained via the Klein combination of
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
, see [Reference Kapovich21, §4.18] for example). The discontinuity domain
$\Gamma _2$
, see [Reference Kapovich21, §4.18] for example). The discontinuity domain
![]() $\Omega $
of
$\Omega $
of
![]() $\Gamma $
in
$\Gamma $
in
![]() $P^1(\mathbb {C})$
is connected and the quotient orbifold
$P^1(\mathbb {C})$
is connected and the quotient orbifold
![]() ${\mathcal O}= \Omega /\Gamma $
is a sphere with six cone points of the orders
${\mathcal O}= \Omega /\Gamma $
is a sphere with six cone points of the orders
![]() $p_i$
,
$p_i$
,
![]() $q_i$
and
$q_i$
and
![]() $r_i$
(
$r_i$
(
![]() $i=1,2$
).
$i=1,2$
).
Being geometrically finite, the group
![]() $\Gamma $
is relatively stable (relative its parabolic elements): let
$\Gamma $
is relatively stable (relative its parabolic elements): let
denote the relative representation variety, which is the subvariety in the representation variety defined by the condition that images of parabolic elements of
![]() $\Gamma $
are again parabolic. Let
$\Gamma $
are again parabolic. Let
![]() $\iota _{\Gamma }:\Gamma \to \mathrm {PSL}(2,\mathbb {C})$
denote the identity embedding. Then there is a small neighborhood U of
$\iota _{\Gamma }:\Gamma \to \mathrm {PSL}(2,\mathbb {C})$
denote the identity embedding. Then there is a small neighborhood U of
![]() $\iota _{\Gamma }$
in
$\iota _{\Gamma }$
in
![]() $\mathrm {Hom}_{\mathrm {par}}(\Gamma ,\mathrm {PSL}(2,\mathbb {C}))$
which consists entirely of faithful geometrically finite representations which are, moreover, given by quasi-conformal conjugations of
$\mathrm {Hom}_{\mathrm {par}}(\Gamma ,\mathrm {PSL}(2,\mathbb {C}))$
which consists entirely of faithful geometrically finite representations which are, moreover, given by quasi-conformal conjugations of
![]() $\Gamma $
. Since the subgroups
$\Gamma $
. Since the subgroups
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
are rigid, there is a neighborhood V of
$\Gamma _2$
are rigid, there is a neighborhood V of
![]() $\iota _{\Gamma }$
such that
$\iota _{\Gamma }$
such that
It follows that the action of
![]() $\Gamma $
on its limit set is structurally stable in
$\Gamma $
on its limit set is structurally stable in
![]() $\mathrm {PSL}(2,\mathbb {C})$
, in particular, algebraically stable. However,
$\mathrm {PSL}(2,\mathbb {C})$
, in particular, algebraically stable. However,
![]() $\Gamma $
is not convex-cocompact. Lastly, the group
$\Gamma $
is not convex-cocompact. Lastly, the group
![]() $\Gamma $
is not rigid, the (complex) dimension of the character variety
$\Gamma $
is not rigid, the (complex) dimension of the character variety
near
![]() $[\iota _{\Gamma }]$
equals the (complex) dimension of the Teichmüller space of
$[\iota _{\Gamma }]$
equals the (complex) dimension of the Teichmüller space of
![]() ${\mathcal O}$
, which is
${\mathcal O}$
, which is
![]() $3$
.
$3$
.
On the other hand, one can show that if
![]() $\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is a finitely generated discrete subgroup which is not a lattice and contains no parabolic von Dyck subgroups, then algebraic stability of
$\Gamma <\mathrm {PSL}(2,\mathbb {C})$
is a finitely generated discrete subgroup which is not a lattice and contains no parabolic von Dyck subgroups, then algebraic stability of
![]() $\Gamma $
implies quasi-convexity of
$\Gamma $
implies quasi-convexity of
![]() $\Gamma $
. We refer the reader to the paper by Matsuzaki [Reference Matsuzaki32] for the precise description of structurally stable finitely generated Kleinian subgroups of
$\Gamma $
. We refer the reader to the paper by Matsuzaki [Reference Matsuzaki32] for the precise description of structurally stable finitely generated Kleinian subgroups of
![]() $\mathrm {PSL}(2,\mathbb {C})$
.
$\mathrm {PSL}(2,\mathbb {C})$
.
Acknowledgments
We thank Bernhard Leeb and Inkang Kim for their interest and encouragement. We are grateful to the referee for reading the manuscript extremely carefully and providing many valuable comments that helped us to clarify and streamline the exposition. We incorporated our result on uniform lattices in the present paper as per the referee’s suggestion as well.
M. Kapovich was partly supported by the NSF grant DMS-16-04241, by KIAS (the Korea Institute for Advanced Study) through the KIAS scholar program, and by a Simons Foundation Fellowship, grant number 391602. S. Kim was supported by the grants NRF-2015R1D1A1A09058742 and NRF-2018R1D1A1B07043321. J. Lee thanks Jeju National University for its hospitality during his visit; he was supported by the grants NRF-2014R1A2A2A01005574, NRF-2017R1A2A2A05001002, and NRF-2019R1F1A1047703.
Competing Interests
None.


















