I. INTRODUCTION
Nowadays, to satisfy the requirement of ubiquitous wireless communications anytime, anywhere, and anyone, more and more new devices are being developed exponentially [1]. In order to support the data traffic due to more and more devices subscribed, 5G wireless communication is expected to achieve 1000 times high mobile data volume [Reference Osseiran2]. However, the microwave spectrum allocation cannot satisfy the huge amount of the 5G wireless communication; therefore, the untapped frequency such as the millimeter band (mmWave) is expected to mitigate the burden [Reference Rappaport3]. Generally, mmWave wireless communication is only analyzed under the background noise. However, the impulsive noise (IN) due to the monitoring applications, ignitions of mobile vehicles [Reference Willig, Matheus and Wolisz4, Reference Ma, So and Gunawan5] also increases the bit error rate (BER) which causes the problem of the connectivity reliability and increases the transmission latency in the event of packet loss [Reference Juwono, Guo, Huang and Wong6] in a harsh industrial environment [Reference Shhab, Rizaner, Ulusoy and Amca7, Reference Cheffena8] which requires low latency and high reliability. Therefore, it is vital to mitigate the impact of the IN in the ultra-reliable low-latency communication (URLLC) [Reference Shafi9, Reference Popovski, Trillingsgaard, Simeone and Durisi10].
Orthogonal frequency division multiplexing (OFDM) technology is widely utilized in many wireless applications including ISDB-T [Reference Takada and Saito11] and 5G [Reference Andrews12]. A OFDM system achieves high spectral efficiency and robustness with multipath fading and IN [Reference Ghosh13]. However, the IN is unneglectable when the interference power of the IN is very large [Reference Ghosh13].
Blanking, clipping, and the combination of the blanking and clipping are the conventional methods to reduce the impact of the IN [Reference Tseng, Han, Mow, Chang and Vinck14–Reference Epple and Schnell18]. The drawback of these methods is degradation of the performance when the useful signal is mistaken as the IN. Therefore, it is challenging to obtain the optimal threshold in order to judge the true useful signal or the IN. Zhidkov [Reference Zhidkov17] has proposed a method to find the theoretical threshold value and Epple and Schnell [Reference Epple and Schnell18] further proposed a method using an adaptive threshold to mitigate the impact of the IN. However, these methods require the parameters of the IN model. On the other hand, Miyamoto et al. [Reference Miyamoto, Katayama and Morinaga19] have proposed the maximum likelihood sequence estimation (MLSE) decoding which compares the received signal with all possible candidates and decides the best signal to improve the performance of single carrier systems over the environments with large IN. Although the system delivers good performance, the complexity is very high. Especially, the complexity of OFDM with MLSE increases exponentially with the number of subcarriers. As a matter of fact, SML has been proposed in [Reference Takahashi, Hamamura and Tachikawa20] to improve the performance of OFDM and Hou and Hase [Reference Hou and Hase21] further show that SML-based OFDM can reconstruct the original signal even if only successive time-domain symbols are missing due to packet loss and the assumption is that noise only includes additive white Gaussian noise (AWGN) noise.
We propose a OFDM receiver utilizing the combination of suboptimal MLSE and blanking (SMLB) to improve the performance with an acceptable complexity. In addition, the proposed system utilizes constant false alarm rate (CFAR) [Reference Skolnik22] to obtain the location of the IN by distinguishing the mixed signal including transmitted signal, background noise, and the IN term [Reference Zahedpour, Ferdosizadeh, Marvasti, Mohimani and Babaie-Zadeh23, Reference Zahedpour, Feizi, Amini, Ferdosizadeh and Marvasti24]. On the other hand, suboptimal MLSE (SML) is utilized in the frequency domain to reconstruct the signal after blanking the time-domain signal. The simulated results show that the proposed system has better performance compared to that of the conventional OFDM with blanking when the power ratio of the IN to the background noise is large in both non-fading and fading channel models.
The remainder of the paper is organized as follows. Section II describes the structure of the system model. The proposed receiver is explained in detail in Section III. Section IV shows the simulated results over the IN environment including the non-multipath and multipath fading channel. Finally, the above-mentioned content is concluded in Section V.
II. SYSTEM MODEL
Let $\mathbf {X}_p=[x_{p}(0),\ldots ,x_{p}(N-1)]^{T}$![]() represent the M-QAM modulated data stream in the frequency domain with $N$
represent the M-QAM modulated data stream in the frequency domain with $N$![]() subcarriers in the $p$
subcarriers in the $p$![]() th OFDM symbol. As Fig. 1 shows that the modulated data bits are transmitted through inverse fast Fourier transform and cyclic prefix (CP) to obtain the time domain symbols $\mathbf {s}_p=[s_{p}(N-N_{cp}), \ldots, s_{p}(N-1), s_{p}(0),\ldots ,s_{p}(N-1)]^{T}$
th OFDM symbol. As Fig. 1 shows that the modulated data bits are transmitted through inverse fast Fourier transform and cyclic prefix (CP) to obtain the time domain symbols $\mathbf {s}_p=[s_{p}(N-N_{cp}), \ldots, s_{p}(N-1), s_{p}(0),\ldots ,s_{p}(N-1)]^{T}$![]() . Here $N_{cp}$
. Here $N_{cp}$![]() is the length of CP and the power of the transmitted signal $\sigma _s^{2}$
is the length of CP and the power of the transmitted signal $\sigma _s^{2}$![]() is calculated as $({1}/{2})E\{|\mathbf {s}_p|^{2}\}$
is calculated as $({1}/{2})E\{|\mathbf {s}_p|^{2}\}$![]() .
.

Fig. 1. Structure of the proposed system.
In this paper, Bernoulli–Gaussian (BG) [Reference Fernandes, Finamore, Ribeiro, Marina and Karamachoski25] is utilized as the IN model for the convenience of analyzing the performance of the proposed system. Note that it can be extended to the other famous IN models such as Middleton Class A model, Gaussian mixture model [Reference Shongwey, Vinck and Ferreira26, Reference Curuk27]. The noise in this paper is given by
where $\mathbf {w}_p=[w_{p}(0),\ldots , w_{p}(N-1)]^{T}$![]() is the background noise and $\mathbf {i}_p=[i_{p}(0),\ldots , i_{p}(N-1)]^{T}$
is the background noise and $\mathbf {i}_p=[i_{p}(0),\ldots , i_{p}(N-1)]^{T}$![]() is the IN which is expressed as
is the IN which is expressed as
Here, $g_{p}(k)$![]() is the complex white Gaussian noise with zero mean and $\alpha \sigma _g^{2}$
is the complex white Gaussian noise with zero mean and $\alpha \sigma _g^{2}$![]() variance (i.e. $\alpha$
variance (i.e. $\alpha$![]() shows that how larger the IN is than the background noise). $b_{p}(k)$
shows that how larger the IN is than the background noise). $b_{p}(k)$![]() is the Bernoulli process with probability $G(b_{p}(k) = 1) = q$
is the Bernoulli process with probability $G(b_{p}(k) = 1) = q$![]() (i.e. $G(b_{p}(k) = 0) = 1 - q$
(i.e. $G(b_{p}(k) = 0) = 1 - q$![]() ). The noise can be generated by the probability density function of the BG which is described as
). The noise can be generated by the probability density function of the BG which is described as
where $q$![]() is the probability of the IN occurrence and $\mathcal {N}(\mathbf {n}_p, 0, \sigma _m^{2})$
is the probability of the IN occurrence and $\mathcal {N}(\mathbf {n}_p, 0, \sigma _m^{2})$![]() follows the Gaussian distribution.
follows the Gaussian distribution.
III. PROPOSED RECEIVER
At the receiver side, the received symbols $\mathbf {y_p}$![]() are expressed as
are expressed as
where $\mathbf {h}_p = [h_{p}(0), h_{p}(1), 0, \ldots , 0]^{T}$![]() is the channel impulse response for the two-path Rayleigh fading model. If the received symbol's power is greater than the threshold obtained by the CFAR detector, then the symbol is blanked. Here, the threshold can be derived based on the variance of the received symbols $\sigma _r^{2}$
is the channel impulse response for the two-path Rayleigh fading model. If the received symbol's power is greater than the threshold obtained by the CFAR detector, then the symbol is blanked. Here, the threshold can be derived based on the variance of the received symbols $\sigma _r^{2}$![]() and the probability of false-alarm ($P_{fa}$
and the probability of false-alarm ($P_{fa}$![]() ). The assumption of the system is that OFDM signal can be modeled as a complex Gaussian process with Rayleigh envelope distribution when the number of subcarriers is sufficient large [Reference Zhidkov17] in the case of only AWGN exists. Based on [Reference Zhidkov17], the received symbols $|\mathbf {y}_p|$
). The assumption of the system is that OFDM signal can be modeled as a complex Gaussian process with Rayleigh envelope distribution when the number of subcarriers is sufficient large [Reference Zhidkov17] in the case of only AWGN exists. Based on [Reference Zhidkov17], the received symbols $|\mathbf {y}_p|$![]() follow the Rayleigh distribution. The $P_{fa}$
follow the Rayleigh distribution. The $P_{fa}$![]() of $|\mathbf {y}_p|$
of $|\mathbf {y}_p|$![]() is expressed as
is expressed as
where $T_{B}$![]() is the blanking threshold. Therefore, $T_{B}$
is the blanking threshold. Therefore, $T_{B}$![]() can be obtained as
can be obtained as
given $F_{Pfa}$![]() . The blanked symbols are described as
. The blanked symbols are described as

After removing CP and accomplishing FFT, we utilize SML to reconstruct the original symbols. The output of SML can be represented as
with $\mathbf {Z}_p=[z(0),\ldots , z(N-1)]^{T}$![]() , $\hat {\mathbf {X}}_p=[\hat {x}(0),\ldots, \hat {x}(N-1)]^{T}$
, $\hat {\mathbf {X}}_p=[\hat {x}(0),\ldots, \hat {x}(N-1)]^{T}$![]() and $\hat {x}(i)\in \{-1, 1\}$
and $\hat {x}(i)\in \{-1, 1\}$![]() for BPSK. Here we assume that the channel is perfectly detected. Therefore, $\mathbf {H}_p$
for BPSK. Here we assume that the channel is perfectly detected. Therefore, $\mathbf {H}_p$![]() can be written as
can be written as

As we know, the computational complexity of MLSE used in the OFDM system increases exponentially as $N^{P}$![]() with the number of subcarriers $N$
with the number of subcarriers $N$![]() and the number of constellation subsets $P$
and the number of constellation subsets $P$![]() (i.e. $P \in \{-1, 1\}$
(i.e. $P \in \{-1, 1\}$![]() for BPSK). In order to reduce the complexity, the proposed receiver utilizes SML whose complexity increases linearly as $MP$
for BPSK). In order to reduce the complexity, the proposed receiver utilizes SML whose complexity increases linearly as $MP$![]() by limiting the candidate constellation points to a given number $M$
by limiting the candidate constellation points to a given number $M$![]() in every iteration.
in every iteration.
We define $\hat {\mathbf {X}}^{(i)(j)}$![]() as the $j$
as the $j$![]() th candidate constellation points of the $i$
th candidate constellation points of the $i$![]() th iteration process. Note that we omit the subscript $p$
th iteration process. Note that we omit the subscript $p$![]() from the above-mentioned parameters for the convenience of analyzing the impact of SML. The steps of SML can be described as follows:
from the above-mentioned parameters for the convenience of analyzing the impact of SML. The steps of SML can be described as follows:
Step 1: Assume that $P$
 is the number of constellation subsets of $\{-1, 1\}$
is the number of constellation subsets of $\{-1, 1\}$ for BPSK. We define $N$
for BPSK. We define $N$ points as $\hat {\mathbf {X}}^{(1)(u)}=[\hat {x}(0),\ldots ,\hat {x}(U-1),\ldots ,0]$
points as $\hat {\mathbf {X}}^{(1)(u)}=[\hat {x}(0),\ldots ,\hat {x}(U-1),\ldots ,0]$ with $\hat {x}(k)\in \{-1, 1\}$
with $\hat {x}(k)\in \{-1, 1\}$ and $k\in [0,\ldots ,U-1]$
and $k\in [0,\ldots ,U-1]$ . In other words, there are $P^{U}$
. In other words, there are $P^{U}$ kinds of $\hat {\mathbf {X}}^{(1)(u)}$
kinds of $\hat {\mathbf {X}}^{(1)(u)}$ (i.e. $u\in [1,\ldots ,P^{U}]$
(i.e. $u\in [1,\ldots ,P^{U}]$ ). Note that $U$
). Note that $U$ denotes the number of candidate constellation points in the first-iteration process. $\hat {\mathbf {Z}}_u^{(1)}$
denotes the number of candidate constellation points in the first-iteration process. $\hat {\mathbf {Z}}_u^{(1)}$ = $[z_u^{(1)}(0),\ldots , z_u^{(1)}(N-1)]$
= $[z_u^{(1)}(0),\ldots , z_u^{(1)}(N-1)]$ are presented as
(10)\begin{align} \hat{\mathbf{Z}}_u^{(1)}=\mathbf{H}\hat{\mathbf{X}}^{(1)(u)}. \end{align}Therefore, the Euclidian distances $d_u^{(1)}$
are presented as
(10)\begin{align} \hat{\mathbf{Z}}_u^{(1)}=\mathbf{H}\hat{\mathbf{X}}^{(1)(u)}. \end{align}Therefore, the Euclidian distances $d_u^{(1)}$
 between $\hat {\mathbf {Z}}_u^{(1)}$
between $\hat {\mathbf {Z}}_u^{(1)}$ and received samples $\mathbf {Z}$
and received samples $\mathbf {Z}$ are evaluated as
(11)\begin{align} d_u^{(1)}=\sum_{l=0}^{U-1}|\hat{z}_u^{(1)}(l)-z(l)|. \end{align}Here there are $P^{U}$
are evaluated as
(11)\begin{align} d_u^{(1)}=\sum_{l=0}^{U-1}|\hat{z}_u^{(1)}(l)-z(l)|. \end{align}Here there are $P^{U}$
 kinds of $\hat {\mathbf {Z}}_u^{(1)}$
kinds of $\hat {\mathbf {Z}}_u^{(1)}$ generated. After sorting $d_u^{(1)}$
generated. After sorting $d_u^{(1)}$ by ascending order, the corresponding first $M (M < P^{U})$
by ascending order, the corresponding first $M (M < P^{U})$ $\hat {\mathbf {Z}}_u^{(1)}$
$\hat {\mathbf {Z}}_u^{(1)}$ are selected to continue to the next iteration as $\hat {\mathbf {Z}}^{(1)}_{(r)}$
are selected to continue to the next iteration as $\hat {\mathbf {Z}}^{(1)}_{(r)}$ $(r = 1,\ldots ,M)$
$(r = 1,\ldots ,M)$ with corresponding $\hat {\mathbf {X}}^{(1)(u)}$
with corresponding $\hat {\mathbf {X}}^{(1)(u)}$ which are stored as $\hat {\mathbf {X}}^{(1)(r)}$
which are stored as $\hat {\mathbf {X}}^{(1)(r)}$ $(r = 1,\ldots ,M)$
$(r = 1,\ldots ,M)$ .
.Step 2: Redefine the $N$
 samples $\hat {\mathbf {X}}^{(2)(u)}$
samples $\hat {\mathbf {X}}^{(2)(u)}$ $(u=1,\ldots ,MP)$
$(u=1,\ldots ,MP)$ as $\hat {\mathbf {X}}^{(2)(u)}=$
as $\hat {\mathbf {X}}^{(2)(u)}=$ [$\hat {\mathbf {X}}^{(1)(r)},\hat {x}(i),0,\ldots ,0$
[$\hat {\mathbf {X}}^{(1)(r)},\hat {x}(i),0,\ldots ,0$ ] and $\hat {x}(i)\in \{-1, 1\}$
] and $\hat {x}(i)\in \{-1, 1\}$ . Therefore, $MP$
. Therefore, $MP$ kinds of vector $\hat {\mathbf {Z}}_u^{(2)}= [\hat {z}_u^{(2)}(0)$
kinds of vector $\hat {\mathbf {Z}}_u^{(2)}= [\hat {z}_u^{(2)}(0)$ , $\ldots \hat {z}_u^{(2)}(N-1)]$
, $\ldots \hat {z}_u^{(2)}(N-1)]$ are presented as
(12)\begin{align} \hat{\mathbf{Z}}_u^{(2)}=\mathbf{H}\hat{\mathbf{X}}^{(2)(u)}. \end{align}The Euclidian distances $d_u^{(2)} (u = 0,\ldots ,MP-1)$
are presented as
(12)\begin{align} \hat{\mathbf{Z}}_u^{(2)}=\mathbf{H}\hat{\mathbf{X}}^{(2)(u)}. \end{align}The Euclidian distances $d_u^{(2)} (u = 0,\ldots ,MP-1)$
 between $\hat {\mathbf {Z}}_u^{(2)}$
between $\hat {\mathbf {Z}}_u^{(2)}$ and the received samples $\mathbf {Z}$
and the received samples $\mathbf {Z}$ are evaluated by
(13)\begin{align} d_u^{(2)}=\sum_{l=0}^{U}|\hat{z}_u^{(2)}(l)-z(l)|. \end{align}The first $M$
are evaluated by
(13)\begin{align} d_u^{(2)}=\sum_{l=0}^{U}|\hat{z}_u^{(2)}(l)-z(l)|. \end{align}The first $M$
 $\hat {\mathbf {Z}}_u^{(2)}$
$\hat {\mathbf {Z}}_u^{(2)}$ , which are smaller Euclidian distances, are selected as $\hat {\mathbf {Z}}^{(2)}_{(r)}(r = 1,\ldots ,M)$
, which are smaller Euclidian distances, are selected as $\hat {\mathbf {Z}}^{(2)}_{(r)}(r = 1,\ldots ,M)$ from $MP$
from $MP$ kinds of $\hat {\mathbf {Z}}_u^{(2)}$
kinds of $\hat {\mathbf {Z}}_u^{(2)}$ with corresponding $\hat {\mathbf {X}}^{(2)(u)}$
with corresponding $\hat {\mathbf {X}}^{(2)(u)}$ which are stored as $\hat {\mathbf {X}}^{(2)(r)}=$
which are stored as $\hat {\mathbf {X}}^{(2)(r)}=$ $[\hat {x}(0),\ldots ,\hat {x}(U-1),\hat {x}(U)$
$[\hat {x}(0),\ldots ,\hat {x}(U-1),\hat {x}(U)$ ]$(r = 1,\ldots ,M)$
]$(r = 1,\ldots ,M)$ .
.Step 3: $MP$
 kinds of $\hat {\mathbf {Z}}_u^{(N-U+1)}$
kinds of $\hat {\mathbf {Z}}_u^{(N-U+1)}$ are obtained by repeating step 2 $(N-U)$
are obtained by repeating step 2 $(N-U)$ times. Finally, the vector $\hat {\mathbf {X}}^{(N-U+1)(1)}$
times. Finally, the vector $\hat {\mathbf {X}}^{(N-U+1)(1)}$ , which is the minimum Euclidian distance, is the desired result.
, which is the minimum Euclidian distance, is the desired result.
IV. PERFORMANCE EVALUATION AND DISCUSSION
A) Proposed receiver for the non-multipath fading channel
The $P_{fa}$![]() versus threshold and BER performance versus threshold are described in Fig. 2. The proposed system can obtain better performance than that of the conventional blanking system in certain range. For example, Fig. 2(a) shows that the best BER of the conventional blanking system is $9.4 \times 10^{-5}$
versus threshold and BER performance versus threshold are described in Fig. 2. The proposed system can obtain better performance than that of the conventional blanking system in certain range. For example, Fig. 2(a) shows that the best BER of the conventional blanking system is $9.4 \times 10^{-5}$![]() , whereas the best BER of the proposed system is $7.8 \times 10^{-8}$
, whereas the best BER of the proposed system is $7.8 \times 10^{-8}$![]() (i.e. $N = 128$
(i.e. $N = 128$![]() ). Thus, in Fig. 2(b), the BER of the proposal can reach $2.0 \times 10^{-4}$
). Thus, in Fig. 2(b), the BER of the proposal can reach $2.0 \times 10^{-4}$![]() (i.e. $N = 128$
(i.e. $N = 128$![]() ) compared to that of the conventional blanking system whose BER is $5.4 \times 10^{-3}$
) compared to that of the conventional blanking system whose BER is $5.4 \times 10^{-3}$![]() in the optimal threshold. The numerous simulated results showed that it is the optimal threshold when $P_{fa}$
in the optimal threshold. The numerous simulated results showed that it is the optimal threshold when $P_{fa}$![]() is about $1.0 \times 10^{-3}$
is about $1.0 \times 10^{-3}$![]() (i.e. $q = 0.01$
(i.e. $q = 0.01$![]() ) and $P_{fa}$
) and $P_{fa}$![]() is about $1.0 \times 10^{-2}$
is about $1.0 \times 10^{-2}$![]() (i.e. $q = 0.1$
(i.e. $q = 0.1$![]() ) given Eb/No = 20 dB. Implicitly, the proposed system has best BER value with $P_{fa} = 1.0 \times 10^{-3}$
) given Eb/No = 20 dB. Implicitly, the proposed system has best BER value with $P_{fa} = 1.0 \times 10^{-3}$![]() in Fig. 3(a) and $P_{fa} = 1.0 \times 10^{-2}$
in Fig. 3(a) and $P_{fa} = 1.0 \times 10^{-2}$![]() in Fig. 3(b) when Eb/No = 20 dB. In addition, the BER performance with $N = 128$
in Fig. 3(b) when Eb/No = 20 dB. In addition, the BER performance with $N = 128$![]() is better than that of $N = 64$
is better than that of $N = 64$![]() in both systems.
in both systems.
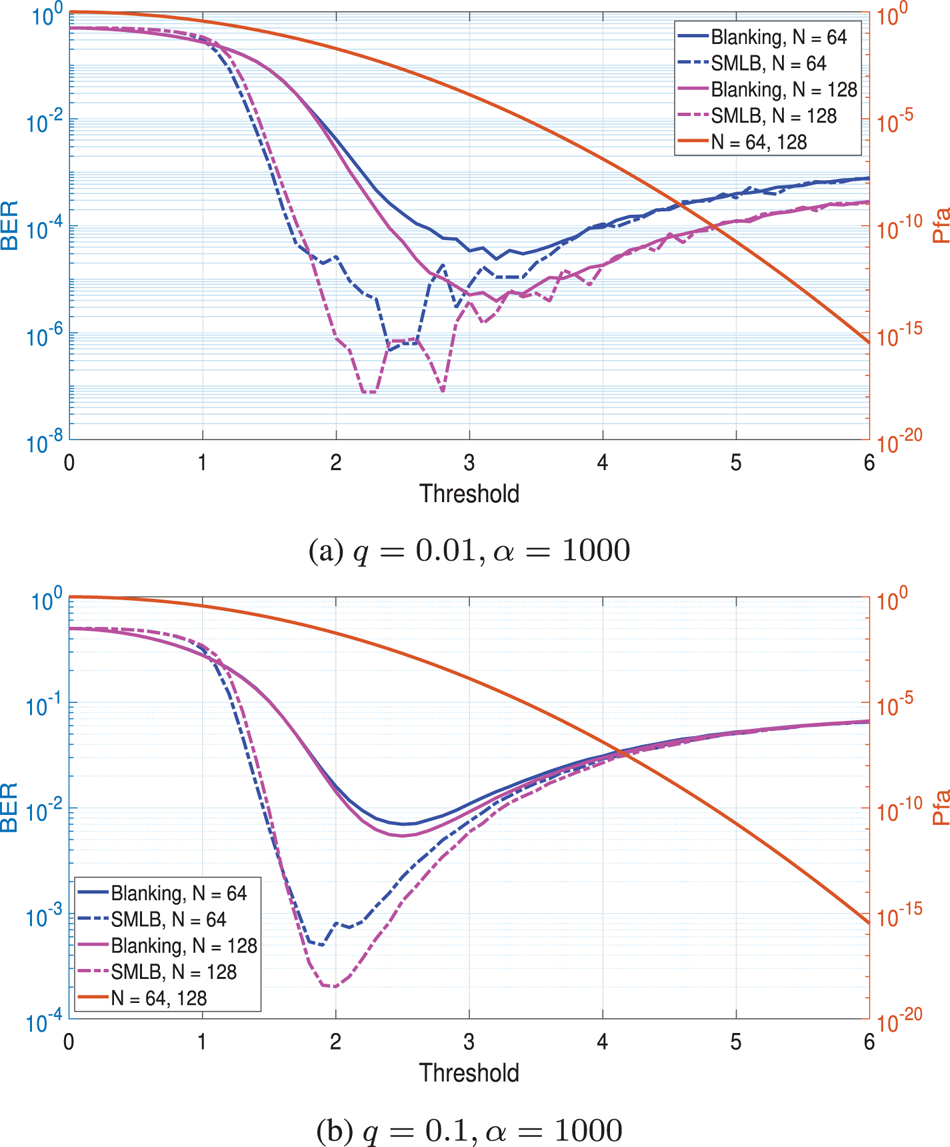
Fig. 2. $P_{fa}$![]() versus threshold, BER performance versus threshold for comparison of the conventional blanking system and the proposed system without CFAR detector in the non-multipath fading channel with $q = 0.01, 0.1$
versus threshold, BER performance versus threshold for comparison of the conventional blanking system and the proposed system without CFAR detector in the non-multipath fading channel with $q = 0.01, 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() given Eb/No = 20 dB when $N = 64, 128$
given Eb/No = 20 dB when $N = 64, 128$![]() . (a) $q = 0.01, \alpha = 1000$
. (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.

Fig. 3. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system in the non-multipath fading channel with $q = 0.01, 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() given $P_{fa}$
given $P_{fa}$![]() ($P_{fa}$
($P_{fa}$![]() = 0.001 and 0.01). (a) $q = 0.01, \alpha = 1000$
= 0.001 and 0.01). (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.
Figure 3 shows the performance of the proposed system over the non-multipath fading channel. The proposed system can obtain better performance compared to that of the conventional with or without blanking and clipping process. For example, in Fig. 3(a), the proposed system can obtain about 10 dB Eb/No improvement to achieve BER = as $1.9 \times 10^{-5}$![]() when $P_{fa}$
when $P_{fa}$![]() = 0.001. On the other hand, the curve in Fig. 3(b) is increasing upward after Eb/No = 15 dB, but it is still better than that of the conventional system. The reason is that when Eb/No becomes larger, the power of the Gaussian noise becomes smaller, however the IN and the expected signal are mixed due to large $\alpha$
= 0.001. On the other hand, the curve in Fig. 3(b) is increasing upward after Eb/No = 15 dB, but it is still better than that of the conventional system. The reason is that when Eb/No becomes larger, the power of the Gaussian noise becomes smaller, however the IN and the expected signal are mixed due to large $\alpha$![]() although the expected signal can be separated from the background noise. In addition, the performance of the OFDM with blanking may be better than that of OFDM with clipping (e.g. Fig. 3(b)) which has similar conclusion to [Reference Zhidkov15]. Note that SML itself does not have an impact on the performance in IN environment. As a matter of fact, Hou and Hase [Reference Hou and Hase21] have mentioned that a partial duration of the OFDM symbols (i.e. add zeros at the end of the received partial signal) can be recovered by SML under the assumption of only AWGN noise exists. Namely, the combination of SML and zero addition which is used to replace the missing part can improve the performance in the AWGN noise. In our case, the blanked part which is regarded as the IN is set to zero (i.e. the other part is only affected by AWGN), SML recovers the blanked signal.
although the expected signal can be separated from the background noise. In addition, the performance of the OFDM with blanking may be better than that of OFDM with clipping (e.g. Fig. 3(b)) which has similar conclusion to [Reference Zhidkov15]. Note that SML itself does not have an impact on the performance in IN environment. As a matter of fact, Hou and Hase [Reference Hou and Hase21] have mentioned that a partial duration of the OFDM symbols (i.e. add zeros at the end of the received partial signal) can be recovered by SML under the assumption of only AWGN noise exists. Namely, the combination of SML and zero addition which is used to replace the missing part can improve the performance in the AWGN noise. In our case, the blanked part which is regarded as the IN is set to zero (i.e. the other part is only affected by AWGN), SML recovers the blanked signal.
Figure 4 shows the BER performance of the proposed system versus conventional with and without blanking system when $q = 0.1$![]() and different $\alpha$
and different $\alpha$![]() . The simulated results show that the proposed system has more ability to improve the performance with increasing $\alpha$
. The simulated results show that the proposed system has more ability to improve the performance with increasing $\alpha$![]() compared to that of the conventional system. When $\alpha$
compared to that of the conventional system. When $\alpha$![]() is small, namely, it is difficult to distinguish the difference between the symbols affected by only background noise or IN. The OFDM with blanking and the proposed system cannot mitigate the impact of the IN. However, when $\alpha$
is small, namely, it is difficult to distinguish the difference between the symbols affected by only background noise or IN. The OFDM with blanking and the proposed system cannot mitigate the impact of the IN. However, when $\alpha$![]() is large, the proposed system can further improve the BER performance of the OFDM with the blanking system. In addition, generally, moderate or high $q$
is large, the proposed system can further improve the BER performance of the OFDM with the blanking system. In addition, generally, moderate or high $q$![]() and $\alpha$
and $\alpha$![]() are more valuable to discuss since IN is a dominant factor to affect the performance of the system.
are more valuable to discuss since IN is a dominant factor to affect the performance of the system.
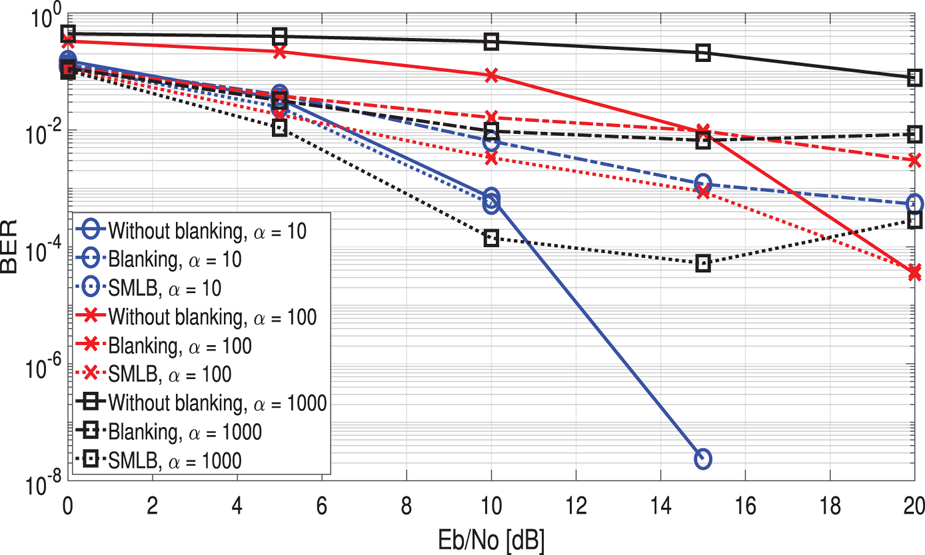
Fig. 4. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system in the non-multipath fading channel with $q = 0.1$![]() and $\alpha = 10, 100, 1000$
and $\alpha = 10, 100, 1000$![]() given $P_{fa} = 0.01$
given $P_{fa} = 0.01$![]() .
.
On the other hand, the proposed system can adjust the number of candidates (i.e. $M$![]() = 32 in this paper) to meet the demand of the trade-off between the BER performance and complexity. The complexity of the proposed system is $P^{U + k} \times (N - U - k)(MP)$
= 32 in this paper) to meet the demand of the trade-off between the BER performance and complexity. The complexity of the proposed system is $P^{U + k} \times (N - U - k)(MP)$![]() . Note that $M$
. Note that $M$![]() is the number of the candidates in every iteration, $P$
is the number of the candidates in every iteration, $P$![]() is the number of the constellation, $U$
is the number of the constellation, $U$![]() is the initial number of subcarriers utilized, $N$
is the initial number of subcarriers utilized, $N$![]() is the number of the subcarriers, and $k$
is the number of the subcarriers, and $k$![]() is the $(k + 1)$
is the $(k + 1)$![]() th iteration where the number of candidates is less than $M$
th iteration where the number of candidates is less than $M$![]() . In this paper, the complexity of the proposed system is $2^{5} \times (123 \times 32 \times 2)$
. In this paper, the complexity of the proposed system is $2^{5} \times (123 \times 32 \times 2)$![]() with $M = 32, P = 2, N = 128$
with $M = 32, P = 2, N = 128$![]() , and $U = 3$
, and $U = 3$![]() . When $M = 16$
. When $M = 16$![]() , the complexity is $2^{4} \times (124 \times 16 \times 2)$
, the complexity is $2^{4} \times (124 \times 16 \times 2)$![]() etc. Figure 5(a) shows that when $q = 0.01, \alpha = 1000$
etc. Figure 5(a) shows that when $q = 0.01, \alpha = 1000$![]() , the BER performance of the system with $M = 8, 16$
, the BER performance of the system with $M = 8, 16$![]() is almost the same as that of the system with $M = 32$
is almost the same as that of the system with $M = 32$![]() . When $q = 0.1$
. When $q = 0.1$![]() as described in Fig. 5(b), the proposed system has worse degradation with $M$
as described in Fig. 5(b), the proposed system has worse degradation with $M$![]() decreasing (i.e. $P_{fa}$
decreasing (i.e. $P_{fa}$![]() = 0.01), however, the proposed system still has better performance than that of the conventional blanking scheme.
= 0.01), however, the proposed system still has better performance than that of the conventional blanking scheme.

Fig. 5. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system using different number of candidates ($M$![]() ) in the non-multipath fading channel with $q = 0.01, 0.1$
) in the non-multipath fading channel with $q = 0.01, 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() given $P_{fa}$
given $P_{fa}$![]() ($P_{fa}$
($P_{fa}$![]() = 0.001 and 0.01) when $N = 128$
= 0.001 and 0.01) when $N = 128$![]() . (a) $q = 0.01, \alpha = 1000$
. (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.
Besides $M$![]() , $U$
, $U$![]() is another parameter of the SML method. When $U \leqslant \log _2{M}$
is another parameter of the SML method. When $U \leqslant \log _2{M}$![]() , the performance or complexity of system is the same as that of the system with $U = \log _2{M}$
, the performance or complexity of system is the same as that of the system with $U = \log _2{M}$![]() , since the removed possible candidates start from the case that the number of candidates is larger than $M$
, since the removed possible candidates start from the case that the number of candidates is larger than $M$![]() . When $U > \log _2{M}$
. When $U > \log _2{M}$![]() , the complexity increases with larger $U$
, the complexity increases with larger $U$![]() . The BER performance versus Eb/No with different $U$
. The BER performance versus Eb/No with different $U$![]() is described in Fig. 6. The simulated results show that small or moderate $U$
is described in Fig. 6. The simulated results show that small or moderate $U$![]() has no effect on the performance of the system whether moderate or high $q$
has no effect on the performance of the system whether moderate or high $q$![]() and $\alpha$
and $\alpha$![]() . For high $U$
. For high $U$![]() , the complexity of the system is approaching to that of the system using MLSE. Therefore, it is not meaningful from the view of SML concept.
, the complexity of the system is approaching to that of the system using MLSE. Therefore, it is not meaningful from the view of SML concept.

Fig. 6. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system using different initial number of subcarriers ($U$![]() ) in the non-multipath fading channel with $q = 0.01, 0.1$
) in the non-multipath fading channel with $q = 0.01, 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() given $P_{fa}$
given $P_{fa}$![]() ($P_{fa}$
($P_{fa}$![]() = 0.001 and 0.01) when $N = 128$
= 0.001 and 0.01) when $N = 128$![]() . (a) $q = 0.01, \alpha = 1000$
. (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.
B) Proposed receiver for the multipath fading channel
Figure 7 describes the $P_{fa}$![]() versus threshold and BER performance versus threshold in the two-path Rayleigh fading channel. The simulated results show that the proposed system can further improve the BER performance of OFDM with blanking when the appropriate threshold is chosen.
versus threshold and BER performance versus threshold in the two-path Rayleigh fading channel. The simulated results show that the proposed system can further improve the BER performance of OFDM with blanking when the appropriate threshold is chosen.
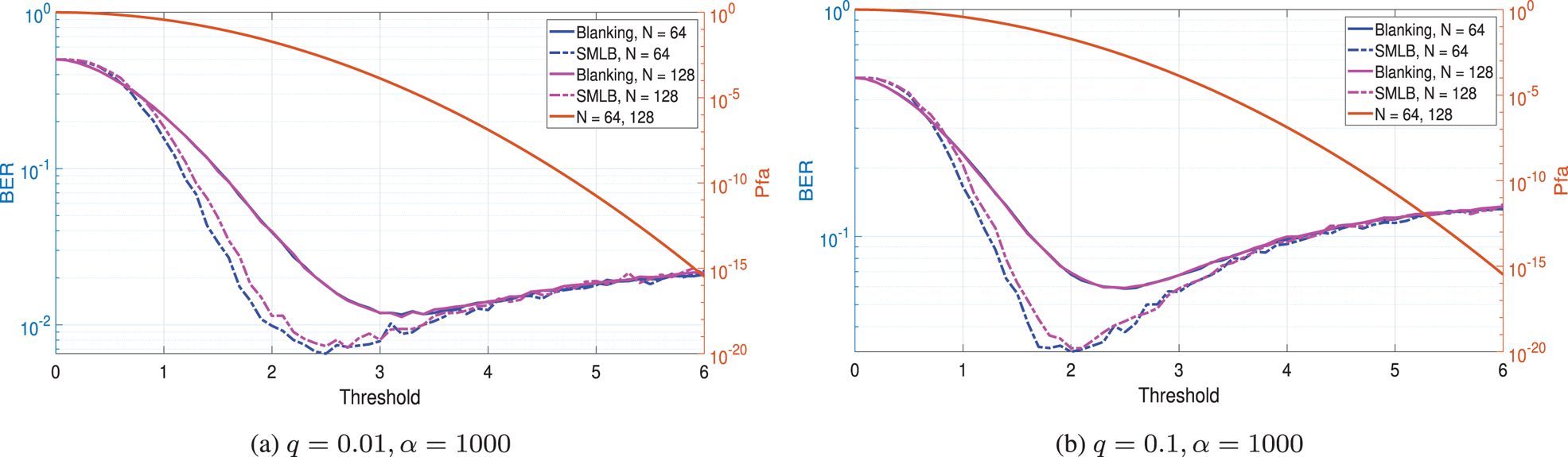
Fig. 7. $P_{fa}$![]() versus threshold, BER performance versus threshold for comparison of the conventional blanking system and the proposed system without CFAR detector in the two-path Rayleigh fading channel with $q = 0.01, 0.1$
versus threshold, BER performance versus threshold for comparison of the conventional blanking system and the proposed system without CFAR detector in the two-path Rayleigh fading channel with $q = 0.01, 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() given Eb/No = 20 dB when $N = 64,128$
given Eb/No = 20 dB when $N = 64,128$![]() . (a) $q = 0.01, \alpha = 1000$
. (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.
The parameter and configuration of the proposed system in the two-path Rayleigh fading channel are shown in Table 1. Figure 8 shows that when $\alpha = 1000$![]() , the proposed system has better performance than that of the conventional with or without blanking and clipping system. For example, the proposed system can achieve about 7 dB Eb/No improvement with BER = $2 \times 10^{-2}$
, the proposed system has better performance than that of the conventional with or without blanking and clipping system. For example, the proposed system can achieve about 7 dB Eb/No improvement with BER = $2 \times 10^{-2}$![]() given $P_{fa}$
given $P_{fa}$![]() = 0.001 in Fig. 8(a). Therefore, the proposed system can achieve the performance improvement by adjusting $P_{fa}$
= 0.001 in Fig. 8(a). Therefore, the proposed system can achieve the performance improvement by adjusting $P_{fa}$![]() value when $\alpha$
value when $\alpha$![]() is very large.
is very large.

Fig. 8. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system in the two-path Rayleigh fading channel with $q = 0.01, 0.1$![]() and $\alpha = 10, 1000$
and $\alpha = 10, 1000$![]() given $P_{fa}$
given $P_{fa}$![]() ($P_{fa}$
($P_{fa}$![]() = 0.001 and 0.01). (a) $q = 0.01, \alpha = 1000$
= 0.001 and 0.01). (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.
Table 1. Parameter and configuration of the proposed system

$(U, M)$![]() : $U$
: $U$![]() is the number of subcarriers used in the first iteration and $M$
is the number of subcarriers used in the first iteration and $M$![]() is the number of the candidate values in every iteration.
is the number of the candidate values in every iteration.
Figure 9 describes the performance of the proposed system with $\alpha$![]() varying in the fading channel. When $\alpha = 10$
varying in the fading channel. When $\alpha = 10$![]() , blanking method is not useful, however, SMLB method can improve the performance of the blanking. When $\alpha = 100$
, blanking method is not useful, however, SMLB method can improve the performance of the blanking. When $\alpha = 100$![]() , the performance is close to that of the system without blanking. The proposed system can achieve about 5 dB Eb/No improvement with BER = $2 \times 10^{-2}$
, the performance is close to that of the system without blanking. The proposed system can achieve about 5 dB Eb/No improvement with BER = $2 \times 10^{-2}$![]() given $P_{fa}$
given $P_{fa}$![]() = 0.01 when $\alpha = 1000$
= 0.01 when $\alpha = 1000$![]() . Therefore, the proposed system is able to obtain better performance than that of the system with or without blanking.
. Therefore, the proposed system is able to obtain better performance than that of the system with or without blanking.
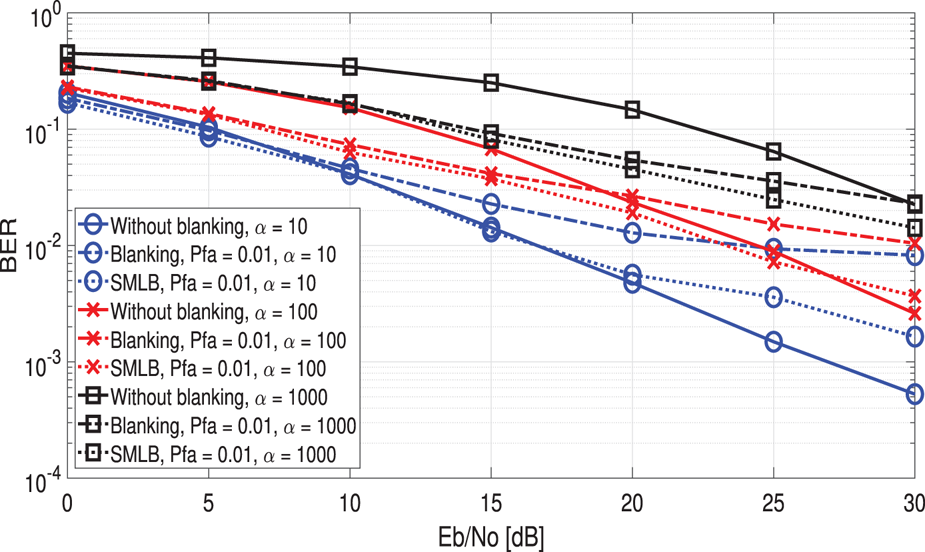
Fig. 9. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system in the two-path Rayleigh fading channel with $q = 0.1$![]() and $\alpha = 10, 100, 1000$
and $\alpha = 10, 100, 1000$![]() given $P_{fa}$
given $P_{fa}$![]() ($P_{fa}$
($P_{fa}$![]() = 0.01).
= 0.01).
In Fig. 10, the performance of the proposed system with $M = 8$![]() is almost the same as that of the system with $M = 32$
is almost the same as that of the system with $M = 32$![]() whether $q = 0.01$
whether $q = 0.01$![]() or $q = 0.1$
or $q = 0.1$![]() . Therefore, the complexity can be further reduced compared to that of the system with $M = 32$
. Therefore, the complexity can be further reduced compared to that of the system with $M = 32$![]() in the Rayleigh fading channel.
in the Rayleigh fading channel.

Fig. 10. BER performance versus Eb/No for comparison of the conventional with or without blanking system and the proposed system using different number of candidates ($M$![]() ) in the two-path Rayleigh fading channel with $q = 0.01, 0.1$
) in the two-path Rayleigh fading channel with $q = 0.01, 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() given $P_{fa}$
given $P_{fa}$![]() ($P_{fa}$
($P_{fa}$![]() = 0.001 and 0.01) when $N = 128$
= 0.001 and 0.01) when $N = 128$![]() . (a) $q = 0.01, \alpha = 1000$
. (a) $q = 0.01, \alpha = 1000$![]() . (b) $q = 0.1, \alpha = 1000$
. (b) $q = 0.1, \alpha = 1000$![]() .
.
C) Application of the proposed receiver in the 5G systems
Juwono et al. [Reference Juwono, Guo, Huang and Wong6] show that IN besides background noise is also one of the factors which affects the performance of the system in a harsh industrial factory which requires low latency and high reliability, namely, it refers to the URLLC which is mainly utilized for automatic factory, real-time remote control [Reference Durisi, Koch and Popovski28]. It is challenging since IN results in the high BER which causes the problem of the connectivity reliability and severe transmission latency in the event of packet loss. As a matter of fact, OFDM can cope well with the IN when the noise power is moderate. However, IN results in the more errors even OFDM system in the high probability of IN occurrence (high $q$![]() ) and high IN power (i.e. it is proportional to $\alpha$
) and high IN power (i.e. it is proportional to $\alpha$![]() ). The simulated results showed that the proposed system can further improve the performance of the conventional blanking system even if the probability of IN occurrence and IN power are very high (e.g. $q = 0.1$
). The simulated results showed that the proposed system can further improve the performance of the conventional blanking system even if the probability of IN occurrence and IN power are very high (e.g. $q = 0.1$![]() and $\alpha = 1000$
and $\alpha = 1000$![]() ) at the same time. Therefore, the proposed system is useful to mitigate the degradation of the system in harsh industrial factory at the acceptable cost of the complexity.
) at the same time. Therefore, the proposed system is useful to mitigate the degradation of the system in harsh industrial factory at the acceptable cost of the complexity.
V. CONCLUSION
In this paper, we proposed an SMLB-based OFDM receiver to mitigate the impact of the IN. The simulated results showed that the proposed system can further improve the performance of OFDM with blanking for high frequent IN occurrence (high $q$![]() ) and high IN power (large $\alpha$
) and high IN power (large $\alpha$![]() ) with appropriate threshold. We pointed out that the proposed system can achieve the trade-off between the performance and the complexity by adjusting the $M$
) with appropriate threshold. We pointed out that the proposed system can achieve the trade-off between the performance and the complexity by adjusting the $M$![]() value. It was effective to mitigate the degradation of the system in harsh industrial factory at the acceptable cost of the complexity.
value. It was effective to mitigate the degradation of the system in harsh industrial factory at the acceptable cost of the complexity.
FINANCIAL SUPPORT
This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
CONFLICT OF INTEREST
None.
Chengbo Liu received her B.S. degree from Shenyang Normal University, China, in 2013 and her M.E. degree in Information Science from the Nara Institute of Science and Technology (NAIST), Japan, in 2017. She is currently pursuing her Ph.D. degree at NAIST. Her current research interests include signal processing of OFDM and MIMO systems.
Na Chen received her Ph.D. degree in 2017 and B.S. degree in 2011 from the Beijing University of Posts and Telecommunications, China. She was a visiting scholar with the University of Texas at Arlington, USA, from September 2015 to September 2016. She is currently with the Nara Institute of Science and Technology, Japan, as an assistant professor. She has been an IEEE and ACM member since 2013, and IEICE member since 2018. Her research interest includes signal processing, wireless communications, and multimedia communication. And her current work focuses on the intelligent signal processing, massive MIMO, and radio over fiber.
Minoru Okada received his B.E. degree in communications engineering from the University of Electro-Communications, Tokyo, Japan, in 1990. He received his M.E. and Ph.D. degrees in communications engineering from Osaka University, Osaka, Japan, in 1992 and 1998, respectively. From 1993 to 2000, he was a Research Associate at Osaka University. From 1999 to 2000, he was a Visiting Research Fellow at the University of Southampton, UK. In 2000, he joined the Graduate School of Information Science, Nara Institute of Science and Technology, Nara, Japan, as an Associate Professor and became a Professor in 2006. His research interest is wireless communications, including WLAN, digital broadcasting, and satellite communications. Dr. Okada is a member of the Institute of Image, Information, and Television Engineers of Japan (ITEJ), the Institute of Television Engineers of Japan, the Institute of Electrical, Information, and Communication Engineers of Japan (IEICE), and the Information Processing Society of Japan (IPSJ).
Yafei Hou received his Ph.D. degrees from Fudan University, China and the Kochi University of Technology (KUT), Japan in 2007. He was a postdoctoral research fellow at Ryukoku University, Japan from August 2007 to September 2010. He was a research scientist at Wave Engineering Laboratories, ATR Institute International, Japan from October 2010 to March 2014. He was an Assistant Professor at the Graduate School of Information Science, Nara Institute of Science and Technology, Japan from April 2014 to March 2017. He became an Assistant Professor at the Graduate School of Natural Science and Technology, Okayama University, Japan from April 2017. He is a guest research scientist at Wave Engineering Laboratories, ATR Institute International, Japan from April 2014. His research interests are communication systems, wireless networks, and signal processing. He has received IEICE (the Institute of Electronics, Information and Communication Engineers) Communications Society Best Paper Awards in 2016, 2020 and Best Tutorial Paper Award in 2017. Dr. Hou is a senior member of IEEE and member of IEICE.





































































