Article contents
The Lehmer Polynomial and Pretzel Links
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we find a formula for the Alexander polynomial 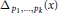 ${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$ of pretzel knots and links with
${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$ of pretzel knots and links with 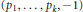 $\left( {{p}_{1}},...,{{p}_{k}},-1 \right)$ twists, where
$\left( {{p}_{1}},...,{{p}_{k}},-1 \right)$ twists, where 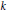 $k$ is odd and
$k$ is odd and 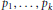 ${{p}_{1}},...,{{p}_{k}}$ are positive integers. The polynomial
${{p}_{1}},...,{{p}_{k}}$ are positive integers. The polynomial 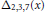 ${{\Delta }_{2,3,7}}\left( x \right)$ is the well-known Lehmer polynomial, which is conjectured to have the smallest Mahler measure among all monic integer polynomials. We confirm that
${{\Delta }_{2,3,7}}\left( x \right)$ is the well-known Lehmer polynomial, which is conjectured to have the smallest Mahler measure among all monic integer polynomials. We confirm that 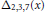 ${{\Delta }_{2,3,7}}\left( x \right)$ has the smallest Mahler measure among the polynomials arising as
${{\Delta }_{2,3,7}}\left( x \right)$ has the smallest Mahler measure among the polynomials arising as 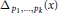 ${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$ .
${{\Delta }_{p1,...,{{p}_{k}}\left( x \right)}}$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001
References
[Boyd]
Boyd, D. W., Speculations concerning the range of Mahler's measure. Canad. Math. Bull. (4) 24 (1981), 453–469.Google Scholar
[C-W]
Cannon, J. and Wagreich, P., Growth functions of surface groups. Math. Ann. 293 (1992), 239–257.Google Scholar
[Floy]
Floyd, W. J., Growth of planar Coxeter groups, P.V. numbers, and Salem numbers. Math. Ann. 293 (1992), 475–483.Google Scholar
[F-P]
Floyd, W. J. and Plotnick, S. P., Symmetries of planar growth functions of Coxeter groups. Invent. Math. 93 (1988), 501–543.Google Scholar
[Kir]
Kirby, R., Problems in Low-Dimensional Topology. In: Geometric Topology (ed.W.H. Kazez), Stud. Adv. Math., Amer.Math. Soc., 1997.Google Scholar
[Leh]
Lehmer, D. H., Factorization of certain cyclotomic functions. Ann. of Math. 34 (1933), 461–469.Google Scholar
[Lev]
Levine, J., Polynomial invariants of knots in codimension 2. Ann. of Math. 2 84 (1966), 537–554.Google Scholar
[Smy]
Smyth, C. J., On the product of the conjugates outside the unit circle of an algebraic integer. Bull. London Math. Soc. 3 (1971), 169–175.Google Scholar

