1. Introduction
Let J be a finite set and
![]() $(A_i+v_i)_{i \in J}$
a tuple of contractive affine self-maps on
$(A_i+v_i)_{i \in J}$
a tuple of contractive affine self-maps on
![]() ${\mathbb{R}}^2$
, where we have written
${\mathbb{R}}^2$
, where we have written
![]() $A+v$
to denote the affine map
$A+v$
to denote the affine map
![]() $x \mapsto Ax+v$
defined on
$x \mapsto Ax+v$
defined on
![]() ${\mathbb{R}}^2$
for all matrices
${\mathbb{R}}^2$
for all matrices
![]() $A \in M_2({\mathbb{R}})$
and translation vectors
$A \in M_2({\mathbb{R}})$
and translation vectors
![]() $v \in {\mathbb{R}}^2$
. If the affine maps
$v \in {\mathbb{R}}^2$
. If the affine maps
![]() $A_i+v_i$
do not have a common fixed point, then we call such a tuple an affine iterated function system. We also write
$A_i+v_i$
do not have a common fixed point, then we call such a tuple an affine iterated function system. We also write
![]() $f_i = A_i+v_i$
for all
$f_i = A_i+v_i$
for all
![]() $i \in J$
and note that the associated tuple of matrices
$i \in J$
and note that the associated tuple of matrices
![]() $(A_i)_{i \in J}$
is an element of
$(A_i)_{i \in J}$
is an element of
![]() $M_2({\mathbb{R}})^J$
.
$M_2({\mathbb{R}})^J$
.
A classical result of Hutchinson [
Reference Hutchinson18
] shows that for each affine iterated function system
![]() $(f_i)_{i \in J}$
there exists a unique non-empty compact set
$(f_i)_{i \in J}$
there exists a unique non-empty compact set
![]() $X^{\prime} \subset {\mathbb{R}}^2$
, called the self-affine set, such that
$X^{\prime} \subset {\mathbb{R}}^2$
, called the self-affine set, such that
In this paper, if
![]() $I = \{i \in J \,:\, A_i \text{ is invertible}\}$
is non-empty, then the self-affine set
$I = \{i \in J \,:\, A_i \text{ is invertible}\}$
is non-empty, then the self-affine set
![]() $X \subset X^{\prime}$
associated to
$X \subset X^{\prime}$
associated to
![]() $(f_i)_{i \in I}$
is called invertible, and if
$(f_i)_{i \in I}$
is called invertible, and if
![]() $J \setminus I$
is non-empty, then the self-affine set X
′ associated to
$J \setminus I$
is non-empty, then the self-affine set X
′ associated to
![]() $(f_i)_{i \in J}$
is called non-invertible. Bárány, Hochman and Rapaport [
Reference Bárány, Hochman and Rapaport2
] and Hochman and Rapaport [
Reference Hochman and Rapaport17
] have recently shown that the Hausdorff dimension reaches a natural upper bound, the affinity dimension, on a large deterministic class of invertible self-affine sets.
$(f_i)_{i \in J}$
is called non-invertible. Bárány, Hochman and Rapaport [
Reference Bárány, Hochman and Rapaport2
] and Hochman and Rapaport [
Reference Hochman and Rapaport17
] have recently shown that the Hausdorff dimension reaches a natural upper bound, the affinity dimension, on a large deterministic class of invertible self-affine sets.
In our main result, Theorem 1·1 below, part (i) shows that generically under a separation condition the dimensions of X
′ and X agree when they are at least 1. Furthermore, if the dimension of X is strictly less than 1, then part (ii) demonstrates that generically the dimensions of X
′ and X are distinct. Regarding part (iii), let us first recall that Marstrand’s projection theorem [
Reference Marstrand24
] gives
![]() ${\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X^{\prime})) = \min\{1,{\textrm{dim}_{\textrm{H}}}(X^{\prime})\}$
for Lebesgue almost all
${\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X^{\prime})) = \min\{1,{\textrm{dim}_{\textrm{H}}}(X^{\prime})\}$
for Lebesgue almost all
![]() $V \in {\mathbb{RP}^{1}}$
. Although the equality holds for generic V, it is often difficult to say whether a particular V satisfies it. The purpose of part (iii) is to verify that the orthogonal complement of the kernel of one of the rank one matrices is such a direction.
$V \in {\mathbb{RP}^{1}}$
. Although the equality holds for generic V, it is often difficult to say whether a particular V satisfies it. The purpose of part (iii) is to verify that the orthogonal complement of the kernel of one of the rank one matrices is such a direction.
The precise definitions of the assumptions used in the theorem will be given in coming sections.
Theorem 1·1. Suppose that X′ and X are the planar self-affine sets associated to affine iterated function systems
![]() $(A_i+v_i)_{i \in J}$
and
$(A_i+v_i)_{i \in J}$
and
![]() $(A_i+v_i)_{i \in I}$
such that
$(A_i+v_i)_{i \in I}$
such that
![]() $A_i \in GL_2({\mathbb{R}})$
for all
$A_i \in GL_2({\mathbb{R}})$
for all
![]() $i \in I \subset J$
, respectively.
$i \in I \subset J$
, respectively.
-
(i) If
 $(A_i)_{i \in I}$
is strictly affine and strongly irreducible such that
$(A_i)_{i \in I}$
is strictly affine and strongly irreducible such that
 ${\textrm{dim}_{\textrm{aff}}}((A_{i})_{i \in I}) \geqslant 1$
and X satisfies the strong open set condition, then for all
${\textrm{dim}_{\textrm{aff}}}((A_{i})_{i \in I}) \geqslant 1$
and X satisfies the strong open set condition, then for all \begin{align*} {\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) &= {\textrm{dim}_{\textrm{H}}}(X), \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X^{\prime})) &= 1 \end{align*}
\begin{align*} {\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) &= {\textrm{dim}_{\textrm{H}}}(X), \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X^{\prime})) &= 1 \end{align*}
 $V \in {\mathbb{RP}^{1}}$
.
$V \in {\mathbb{RP}^{1}}$
.
-
(ii) If
 $(A_i)_{i \in J}$
is dominated or irreducible such that
$(A_i)_{i \in J}$
is dominated or irreducible such that
 $\max_{i \in J} \|A_i\| \lt 1/2$
, contains a rank one matrix, and
$\max_{i \in J} \|A_i\| \lt 1/2$
, contains a rank one matrix, and
 ${\textrm{dim}_{\textrm{aff}}}((A_i)_{i \in I}) \lt 1$
, then for
${\textrm{dim}_{\textrm{aff}}}((A_i)_{i \in I}) \lt 1$
, then for \begin{equation*} {\textrm{dim}_{\textrm{H}}}(X_{\mathsf{v}}^{\prime}) \gt {\overline{\textrm{dim}}_{\textrm{M}}}(X_{\mathsf{v}}) \end{equation*}
\begin{equation*} {\textrm{dim}_{\textrm{H}}}(X_{\mathsf{v}}^{\prime}) \gt {\overline{\textrm{dim}}_{\textrm{M}}}(X_{\mathsf{v}}) \end{equation*}
 ${\mathcal{L}}^{2\# J}$
-almost all translation vectors
${\mathcal{L}}^{2\# J}$
-almost all translation vectors
 $\mathsf{v} = (v_i)_{i \in J} \in ({\mathbb{R}}^2)^{\# J}$
.
$\mathsf{v} = (v_i)_{i \in J} \in ({\mathbb{R}}^2)^{\# J}$
.
-
(iii) If
 $(A_i)_{i \in J}$
contains a rank one matrix,
$(A_i)_{i \in J}$
contains a rank one matrix,
 $(A_i)_{i \in I}$
is strictly affine and strongly irreducible such that
$(A_i)_{i \in I}$
is strictly affine and strongly irreducible such that
 ${\textrm{dim}_{\textrm{aff}}}((A_i)_{i \in I}) \lt 1$
, and X satisfies the strong open set condition, then there exists a rank one matrix A in
${\textrm{dim}_{\textrm{aff}}}((A_i)_{i \in I}) \lt 1$
, and X satisfies the strong open set condition, then there exists a rank one matrix A in
 ${\mathsf{A}}$
such that
${\mathsf{A}}$
such that  \begin{equation*} {\textrm{dim}_{\textrm{H}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) \leqslant 1. \end{equation*}
\begin{equation*} {\textrm{dim}_{\textrm{H}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) \leqslant 1. \end{equation*}
We remark that Bárány and Körtvélyesi [ Reference Bárány and Körtvélyesi5 ] have recently continued the above study. They have demonstrated that if the affinity dimension is strictly less than one, then there exist two large parameter sets for the defining matrices so that in the first one, the Hausdorff dimension of the non-invertible self-affine set equals the affinity dimension, and in the second one, the Hausdorff dimension is strictly smaller than the affinity dimension. This observation proposes that determining the Hausdorff dimension in this situation requires a better understanding of the geometry.
The remainder of the paper is organised as follows. In Section 2, we compare the behaviour of the pressures and study the continuity. In particular, for dominated and irreducible matrices, we completely characterise the continuity of the pressure in the non-invertible case. In Section 3, we uncover how the study of non-invertible self-affine sets is connected to the theory of sub-self-affine and inhomogeneous self-affine sets, and prove the main result.
2. Products of matrices
2·1. Rank one matrices
We denote the collection of all
![]() $2 \times 2$
matrices with real entries by
$2 \times 2$
matrices with real entries by
![]() $M_2({\mathbb{R}})$
, the general linear group of degree 2 over
$M_2({\mathbb{R}})$
, the general linear group of degree 2 over
![]() ${\mathbb{R}}$
by
${\mathbb{R}}$
by
![]() $GL_2({\mathbb{R}}) \subset M_2({\mathbb{R}})$
, and the orthogonal group in dimension 2 over
$GL_2({\mathbb{R}}) \subset M_2({\mathbb{R}})$
, and the orthogonal group in dimension 2 over
![]() ${\mathbb{R}}$
by
${\mathbb{R}}$
by
![]() $O_2({\mathbb{R}}) \subset GL_2({\mathbb{R}})$
. A matrix
$O_2({\mathbb{R}}) \subset GL_2({\mathbb{R}})$
. A matrix
![]() $A \in GL_2({\mathbb{R}})$
is called proximal if it has two real eigenvalues with different absolute values. If
$A \in GL_2({\mathbb{R}})$
is called proximal if it has two real eigenvalues with different absolute values. If
![]() $A \in M_2({\mathbb{R}})$
, then the singular values of A are defined to be the non-negative square roots of the eigenvalues of the positive-semidefinite matrix
$A \in M_2({\mathbb{R}})$
, then the singular values of A are defined to be the non-negative square roots of the eigenvalues of the positive-semidefinite matrix
![]() ${A^\top}A$
and are denoted by
${A^\top}A$
and are denoted by
![]() $\alpha_1(A)$
and
$\alpha_1(A)$
and
![]() $\alpha_2(A)$
in non-increasing order. Recall that the rank of A is the number of non-zero singular values of A. The identities
$\alpha_2(A)$
in non-increasing order. Recall that the rank of A is the number of non-zero singular values of A. The identities
![]() $\alpha_1(A)=\|A\|$
and
$\alpha_1(A)=\|A\|$
and
![]() $\alpha_1(A)\alpha_2(A) = |\det(A)|$
for all
$\alpha_1(A)\alpha_2(A) = |\det(A)|$
for all
![]() $A \in M_2({\mathbb{R}})$
are standard, as is the identity
$A \in M_2({\mathbb{R}})$
are standard, as is the identity
![]() $\alpha_2(A)=\|A^{-1}\|^{-1}$
in the case where A is invertible. For each
$\alpha_2(A)=\|A^{-1}\|^{-1}$
in the case where A is invertible. For each
![]() $A \in M_2({\mathbb{R}})$
and
$A \in M_2({\mathbb{R}})$
and
![]() $s \geqslant 0$
we define the singular value function by setting
$s \geqslant 0$
we define the singular value function by setting
 \begin{equation*} \varphi^s(A)= \begin{cases} \alpha_1(A)^s, &\text{if } 0 \leqslant s \leqslant 1, \\[4pt] \alpha_1(A)\alpha_2(A)^{s-1}, &\text{if } 1 \lt s \leqslant 2, \\[4pt] |\det(A)|^{s/2}, &\text{if } 2 \lt s \lt \infty, \end{cases}\end{equation*}
\begin{equation*} \varphi^s(A)= \begin{cases} \alpha_1(A)^s, &\text{if } 0 \leqslant s \leqslant 1, \\[4pt] \alpha_1(A)\alpha_2(A)^{s-1}, &\text{if } 1 \lt s \leqslant 2, \\[4pt] |\det(A)|^{s/2}, &\text{if } 2 \lt s \lt \infty, \end{cases}\end{equation*}
where we interpret
![]() $0^0 = 1$
. The value
$0^0 = 1$
. The value
![]() ${\varphi}^s(A)$
represents a measurement of the s-dimensional volume of the image of the Euclidean unit ball under A. Since
${\varphi}^s(A)$
represents a measurement of the s-dimensional volume of the image of the Euclidean unit ball under A. Since
![]() $\alpha_1(A)\alpha_2(A)^{s-1} = \alpha_1(A)^{2-s}|\det(A)|^{s-1}$
for all
$\alpha_1(A)\alpha_2(A)^{s-1} = \alpha_1(A)^{2-s}|\det(A)|^{s-1}$
for all
![]() $1 \lt s \leqslant 2$
, the inequality
$1 \lt s \leqslant 2$
, the inequality
![]() $\varphi^s(AB) \leqslant \varphi^s(A)\varphi^s(B)$
is valid for all
$\varphi^s(AB) \leqslant \varphi^s(A)\varphi^s(B)$
is valid for all
![]() $s \geqslant 0$
. In other words, the singular value function is sub-multiplicative.
$s \geqslant 0$
. In other words, the singular value function is sub-multiplicative.
Note that if
![]() $A \in M_2({\mathbb{R}})$
has rank one, then
$A \in M_2({\mathbb{R}})$
has rank one, then
![]() ${\varphi}^s(A) = 0$
for all
${\varphi}^s(A) = 0$
for all
![]() $s\gt1$
. Recalling that A has rank zero if and only if A is the zero matrix, we see that
$s\gt1$
. Recalling that A has rank zero if and only if A is the zero matrix, we see that
![]() ${\varphi}^s(A)=0$
for all
${\varphi}^s(A)=0$
for all
![]() $s \gt 0$
. Let us next recall that rank one matrices are projections. Let
$s \gt 0$
. Let us next recall that rank one matrices are projections. Let
![]() ${\mathbb{RP}^{1}}$
be the real projective line, that is, the set of all lines through the origin in
${\mathbb{RP}^{1}}$
be the real projective line, that is, the set of all lines through the origin in
![]() ${\mathbb{R}}^2$
. If
${\mathbb{R}}^2$
. If
![]() $V,W \in {\mathbb{RP}^{1}}$
, then the projection
$V,W \in {\mathbb{RP}^{1}}$
, then the projection
![]() ${\textrm{proj}}_V^W \colon {\mathbb{R}}^2 \to V$
is the linear map such that
${\textrm{proj}}_V^W \colon {\mathbb{R}}^2 \to V$
is the linear map such that
![]() ${\textrm{proj}}_V^W|_V=\textrm{Id}|_V$
and
${\textrm{proj}}_V^W|_V=\textrm{Id}|_V$
and
![]() $\ker({\textrm{proj}}_V^W)=W$
. Furthermore, the orthogonal projection
$\ker({\textrm{proj}}_V^W)=W$
. Furthermore, the orthogonal projection
![]() ${\textrm{proj}}_V^{V^\bot}$
onto the subspace V is denoted by
${\textrm{proj}}_V^{V^\bot}$
onto the subspace V is denoted by
![]() ${\textrm{proj}}_V$
. The following lemma is well known. But, as the proof is short, we provide the reader with full details.
${\textrm{proj}}_V$
. The following lemma is well known. But, as the proof is short, we provide the reader with full details.
Lemma 2·1. A matrix
![]() $A \in M_2({\mathbb{R}})$
has rank one if and only if there exist
$A \in M_2({\mathbb{R}})$
has rank one if and only if there exist
![]() $v,w \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
such that
$v,w \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
such that
![]() $A = vw^\top$
. In this case,
$A = vw^\top$
. In this case,
 \begin{equation*} A = \begin{cases} \langle v,w \rangle{\textrm{proj}}_{{\textrm{im}}(A)}^{\ker(A)}, & if\ \textit{A}\ is\ not\ nilpotent, \\[4pt] |v||w|R{\textrm{proj}}_{\ker(A)^\perp}, & if\ \textit{A}\ is\ nilpotent, \end{cases} \end{equation*}
\begin{equation*} A = \begin{cases} \langle v,w \rangle{\textrm{proj}}_{{\textrm{im}}(A)}^{\ker(A)}, & if\ \textit{A}\ is\ not\ nilpotent, \\[4pt] |v||w|R{\textrm{proj}}_{\ker(A)^\perp}, & if\ \textit{A}\ is\ nilpotent, \end{cases} \end{equation*}
where
![]() $R \in O_2({\mathbb{R}})$
is a rotation by an angle
$R \in O_2({\mathbb{R}})$
is a rotation by an angle
![]() $\pi/2$
. In particular, A(X) is bi-Lipschitz equivalent to
$\pi/2$
. In particular, A(X) is bi-Lipschitz equivalent to
![]() ${\textrm{proj}}_{\ker(A)^\bot}(X)$
for all
${\textrm{proj}}_{\ker(A)^\bot}(X)$
for all
![]() $X \subset {\mathbb{R}}^2$
.
$X \subset {\mathbb{R}}^2$
.
Proof. Let us first prove the characterisation of rank one matrices. If
![]() $A = vw^\top$
for some
$A = vw^\top$
for some
![]() $v,w \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
, then
$v,w \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
, then
![]() $Ax = vw^\top x = \langle w,x \rangle v$
for all
$Ax = vw^\top x = \langle w,x \rangle v$
for all
![]() $x \in {\mathbb{R}}^2$
. Therefore, A maps every x to a scalar multiple of v,
$x \in {\mathbb{R}}^2$
. Therefore, A maps every x to a scalar multiple of v,
![]() ${\textrm{rank}}(A)=1$
, and
${\textrm{rank}}(A)=1$
, and
![]() ${\textrm{im}}(A) = {\textrm{span}}(v)$
. If
${\textrm{im}}(A) = {\textrm{span}}(v)$
. If
![]() $x \in {\textrm{span}}(w)^\bot$
, then
$x \in {\textrm{span}}(w)^\bot$
, then
![]() $Ax = vw^\top x = \langle w,x \rangle v = 0$
and
$Ax = vw^\top x = \langle w,x \rangle v = 0$
and
![]() $\ker(A)={\textrm{span}}(w)^\bot$
. Conversely, if
$\ker(A)={\textrm{span}}(w)^\bot$
. Conversely, if
![]() ${\textrm{rank}}(A)=1$
, then there is
${\textrm{rank}}(A)=1$
, then there is
![]() $v \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
such that Ax is a scalar multiple of v for all
$v \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
such that Ax is a scalar multiple of v for all
![]() $x \in {\mathbb{R}}^2$
. In particular, this is true when
$x \in {\mathbb{R}}^2$
. In particular, this is true when
![]() $x = (1,0)$
and
$x = (1,0)$
and
![]() $x = (0, 1)$
. That is, there are
$x = (0, 1)$
. That is, there are
![]() $w_1,w_2 \in {\mathbb{R}} \setminus \{0\}$
such that
$w_1,w_2 \in {\mathbb{R}} \setminus \{0\}$
such that
![]() $A(1,0)=w_1v$
and
$A(1,0)=w_1v$
and
![]() $A(0, 1)=w_2v$
. In other words,
$A(0, 1)=w_2v$
. In other words,
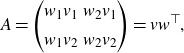 \begin{equation*} A = \begin{pmatrix} w_1v_1 & w_2v_1 \\[4pt] w_1v_2 & w_2v_2 \end{pmatrix} = vw^\top, \end{equation*}
\begin{equation*} A = \begin{pmatrix} w_1v_1 & w_2v_1 \\[4pt] w_1v_2 & w_2v_2 \end{pmatrix} = vw^\top, \end{equation*}
where
![]() $w = (w_1,w_2) \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
.
$w = (w_1,w_2) \in {\mathbb{R}}^2 \setminus \{(0,0)\}$
.
Let us then show that a rank one matrix A is a projection. If A is not nilpotent, then
![]() ${\textrm{span}}(v) = {\textrm{im}}(A) \ne \ker(A) = {\textrm{span}}(w)^\bot$
. Since
${\textrm{span}}(v) = {\textrm{im}}(A) \ne \ker(A) = {\textrm{span}}(w)^\bot$
. Since
![]() $Ax = vw^\top x = \langle x,w \rangle v$
and it is easy to see that
$Ax = vw^\top x = \langle x,w \rangle v$
and it is easy to see that
for all
![]() $x \in {\mathbb{R}}^2$
, we have shown the first case. If A is nilpotent, then
$x \in {\mathbb{R}}^2$
, we have shown the first case. If A is nilpotent, then
![]() ${\textrm{span}}(v) = {\textrm{im}}(A) = \ker(A) = {\textrm{span}}(w)^\bot$
. Since
${\textrm{span}}(v) = {\textrm{im}}(A) = \ker(A) = {\textrm{span}}(w)^\bot$
. Since
![]() $Rw/|w| = v/|v|$
, where
$Rw/|w| = v/|v|$
, where
![]() $R \in O_2({\mathbb{R}})$
is a rotation by an angle
$R \in O_2({\mathbb{R}})$
is a rotation by an angle
![]() $\pi/2$
, we have
$\pi/2$
, we have
and hence,
as claimed.
Since the last claim follows immediately from the the fact that a rank one matrix is a projection, we have finished the proof.
2·2. Pressure
Let J be a finite set and
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
be a tuple of matrices. We say that
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
be a tuple of matrices. We say that
![]() ${\mathsf{A}}$
is irreducible if there does not exist
${\mathsf{A}}$
is irreducible if there does not exist
![]() $V \in {\mathbb{RP}^{1}}$
such that
$V \in {\mathbb{RP}^{1}}$
such that
![]() $A_iV \subset V$
for all
$A_iV \subset V$
for all
![]() $i \in J$
; otherwise
$i \in J$
; otherwise
![]() ${\mathsf{A}}$
is reducible. Note that the irreducibility is equivalent to the property that the matrices in
${\mathsf{A}}$
is reducible. Note that the irreducibility is equivalent to the property that the matrices in
![]() ${\mathsf{A}}$
do not have a common eigenvector. Therefore,
${\mathsf{A}}$
do not have a common eigenvector. Therefore,
![]() ${\mathsf{A}}$
is reducible if and only if the matrices in
${\mathsf{A}}$
is reducible if and only if the matrices in
![]() ${\mathsf{A}}$
can simultaneously be presented (in some coordinate system) as upper triangular matrices. The tuple
${\mathsf{A}}$
can simultaneously be presented (in some coordinate system) as upper triangular matrices. The tuple
![]() ${\mathsf{A}}$
is strongly irreducible if there does not exist a finite set
${\mathsf{A}}$
is strongly irreducible if there does not exist a finite set
![]() $\mathcal{V} \subset {\mathbb{RP}^{1}}$
such that
$\mathcal{V} \subset {\mathbb{RP}^{1}}$
such that
![]() $A_i\mathcal{V}=\mathcal{V}$
for all
$A_i\mathcal{V}=\mathcal{V}$
for all
![]() $i\in J$
.
$i\in J$
.
We call a proper subset
![]() ${\mathcal{C}}\subset{\mathbb{RP}^{1}}$
a multicone if it is a finite union of closed non-trivial projective intervals. We say that
${\mathcal{C}}\subset{\mathbb{RP}^{1}}$
a multicone if it is a finite union of closed non-trivial projective intervals. We say that
![]() ${\mathsf{A}}$
is dominated if each matrix
${\mathsf{A}}$
is dominated if each matrix
![]() $A_i$
is non-zero and there exists a multicone
$A_i$
is non-zero and there exists a multicone
![]() ${\mathcal{C}}\subset{\mathbb{RP}^{1}}$
such that
${\mathcal{C}}\subset{\mathbb{RP}^{1}}$
such that
![]() $A_i{\mathcal{C}}\subset{\mathcal{C}}^o$
for all
$A_i{\mathcal{C}}\subset{\mathcal{C}}^o$
for all
![]() $i \in J$
, where
$i \in J$
, where
![]() ${\mathcal{C}}^o$
is the interior of
${\mathcal{C}}^o$
is the interior of
![]() ${\mathcal{C}}$
. Conversely, if a multicone
${\mathcal{C}}$
. Conversely, if a multicone
![]() ${\mathcal{C}}\subset{\mathbb{RP}^{1}}$
satisfies such a condition, then we say that
${\mathcal{C}}\subset{\mathbb{RP}^{1}}$
satisfies such a condition, then we say that
![]() ${\mathcal{C}}$
is a strongly invariant multicone for
${\mathcal{C}}$
is a strongly invariant multicone for
![]() ${\mathsf{A}}$
. For example, the first quadrant is strongly invariant for any tuple of positive matrices. Note that a dominated tuple is not necessarily irreducible and vice versa. If
${\mathsf{A}}$
. For example, the first quadrant is strongly invariant for any tuple of positive matrices. Note that a dominated tuple is not necessarily irreducible and vice versa. If
![]() ${\mathsf{A}} \in GL_2({\mathbb{R}})^J$
is dominated and irreducible, then, by [
Reference Bárány, Käenmäki and Yu4
, lemma 2·10],
${\mathsf{A}} \in GL_2({\mathbb{R}})^J$
is dominated and irreducible, then, by [
Reference Bárány, Käenmäki and Yu4
, lemma 2·10],
![]() ${\mathsf{A}}$
is strongly irreducible.
${\mathsf{A}}$
is strongly irreducible.
We let
![]() $J^*$
denote the set of all finite words
$J^*$
denote the set of all finite words
![]() $\{ \varnothing \} \cup \bigcup_{n \in {\mathbb{N}}} J^n$
, where
$\{ \varnothing \} \cup \bigcup_{n \in {\mathbb{N}}} J^n$
, where
![]() $\varnothing$
satisfies
$\varnothing$
satisfies
![]() $\varnothing{\texttt{i}} = {\texttt{i}}\varnothing = {\texttt{i}}$
for all
$\varnothing{\texttt{i}} = {\texttt{i}}\varnothing = {\texttt{i}}$
for all
![]() ${\texttt{i}} \in J^*$
. For notational convenience, we set
${\texttt{i}} \in J^*$
. For notational convenience, we set
![]() $J^0 = \{ \varnothing \}$
. The set
$J^0 = \{ \varnothing \}$
. The set
![]() $J^{\mathbb{N}}$
is the collection of all infinite words. We define the left shift
$J^{\mathbb{N}}$
is the collection of all infinite words. We define the left shift
![]() $\sigma \colon J^{\mathbb{N}} \to J^{\mathbb{N}}$
by setting
$\sigma \colon J^{\mathbb{N}} \to J^{\mathbb{N}}$
by setting
![]() $\sigma{\texttt{i}} = i_2i_3\cdots$
for all
$\sigma{\texttt{i}} = i_2i_3\cdots$
for all
![]() ${\texttt{i}} = i_1i_2\cdots \in J^{\mathbb{N}}$
. The concatenation of two words
${\texttt{i}} = i_1i_2\cdots \in J^{\mathbb{N}}$
. The concatenation of two words
![]() ${\texttt{i}} \in J^*$
and
${\texttt{i}} \in J^*$
and
![]() ${\texttt{j}} \in J^* \cup J^{\mathbb{N}}$
is denoted by
${\texttt{j}} \in J^* \cup J^{\mathbb{N}}$
is denoted by
![]() ${\texttt{i}}{\texttt{j}} \in J^* \cup J^{\mathbb{N}}$
and the length of
${\texttt{i}}{\texttt{j}} \in J^* \cup J^{\mathbb{N}}$
and the length of
![]() ${\texttt{i}} \in J^* \cup J^{\mathbb{N}}$
is denoted by
${\texttt{i}} \in J^* \cup J^{\mathbb{N}}$
is denoted by
![]() $|{\texttt{i}}|$
. If
$|{\texttt{i}}|$
. If
![]() ${\texttt{j}} \in J^* \cup J^{\mathbb{N}}$
and
${\texttt{j}} \in J^* \cup J^{\mathbb{N}}$
and
![]() $1 \leqslant n \lt |{\texttt{j}}|$
, then we define
$1 \leqslant n \lt |{\texttt{j}}|$
, then we define
![]() ${\texttt{j}}|_n$
to be the unique word
${\texttt{j}}|_n$
to be the unique word
![]() ${\texttt{i}} \in J^n$
for which
${\texttt{i}} \in J^n$
for which
![]() ${\texttt{i}}{\texttt{k}} = {\texttt{j}}$
for some
${\texttt{i}}{\texttt{k}} = {\texttt{j}}$
for some
![]() ${\texttt{k}} \in J^* \cup J^{\mathbb{N}}$
. Write
${\texttt{k}} \in J^* \cup J^{\mathbb{N}}$
. Write
![]() ${\texttt{i}}|_0 = \varnothing$
. If
${\texttt{i}}|_0 = \varnothing$
. If
![]() ${\texttt{i}} \in J^* \setminus \{\varnothing\}$
, then
${\texttt{i}} \in J^* \setminus \{\varnothing\}$
, then
![]() ${\texttt{i}}^- = {\texttt{i}}|_{|{\texttt{i}}|-1}$
is the word obtained from
${\texttt{i}}^- = {\texttt{i}}|_{|{\texttt{i}}|-1}$
is the word obtained from
![]() ${\texttt{i}}$
by deleting its last element. Furthermore, if
${\texttt{i}}$
by deleting its last element. Furthermore, if
![]() ${\texttt{i}} \in J^n$
for some
${\texttt{i}} \in J^n$
for some
![]() $n \in {\mathbb{N}}$
, then we set
$n \in {\mathbb{N}}$
, then we set
![]() $[{\texttt{i}}] = \{{\texttt{j}} \in J^{\mathbb{N}} \,:\, {\texttt{j}}|_n={\texttt{i}}\}$
. The set
$[{\texttt{i}}] = \{{\texttt{j}} \in J^{\mathbb{N}} \,:\, {\texttt{j}}|_n={\texttt{i}}\}$
. The set
![]() $[{\texttt{i}}]$
is called a cylinder set. We write
$[{\texttt{i}}]$
is called a cylinder set. We write
![]() $A_{\texttt{i}} = A_{i_1} \cdots A_{i_n}$
for all
$A_{\texttt{i}} = A_{i_1} \cdots A_{i_n}$
for all
![]() ${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
![]() $n \in {\mathbb{N}}$
. We say that
$n \in {\mathbb{N}}$
. We say that
![]() $\mathsf{A} \in GL_2({\mathbb{R}})^J$
is strictly affine if there is
$\mathsf{A} \in GL_2({\mathbb{R}})^J$
is strictly affine if there is
![]() ${\texttt{i}} \in I^*$
such that
${\texttt{i}} \in I^*$
such that
![]() $A_{\texttt{i}}$
is proximal. Recall that
$A_{\texttt{i}}$
is proximal. Recall that
![]() $A \in GL_2({\mathbb{R}})$
is proximal if it has two real eigenvalues with different absolute values. By [
Reference Bárány, Käenmäki and Morris3
, corollary 2·4], a dominated tuple in
$A \in GL_2({\mathbb{R}})$
is proximal if it has two real eigenvalues with different absolute values. By [
Reference Bárány, Käenmäki and Morris3
, corollary 2·4], a dominated tuple in
![]() $GL_2({\mathbb{R}})^J$
is strictly affine.
$GL_2({\mathbb{R}})^J$
is strictly affine.
If
![]() $\Gamma \subset J^{\mathbb{N}}$
is a non-empty compact set such that
$\Gamma \subset J^{\mathbb{N}}$
is a non-empty compact set such that
![]() $\sigma(\Gamma) \subset \Gamma$
, then we define
$\sigma(\Gamma) \subset \Gamma$
, then we define
![]() $\Gamma_n = \{{\texttt{i}}|_n \in J^n \,:\, {\texttt{i}} \in \Gamma\}$
and
$\Gamma_n = \{{\texttt{i}}|_n \in J^n \,:\, {\texttt{i}} \in \Gamma\}$
and
![]() $\Gamma_* = \bigcup_{n \in {\mathbb{N}}} \Gamma_n$
. We keep denoting
$\Gamma_* = \bigcup_{n \in {\mathbb{N}}} \Gamma_n$
. We keep denoting
![]() $(I^{\mathbb{N}})_n$
and
$(I^{\mathbb{N}})_n$
and
![]() $(I^{\mathbb{N}})_*$
by
$(I^{\mathbb{N}})_*$
by
![]() $I^n$
and
$I^n$
and
![]() $I^*$
, respectively, for all
$I^*$
, respectively, for all
![]() $I \subset J$
and
$I \subset J$
and
![]() $n \in {\mathbb{N}}$
. Given a tuple
$n \in {\mathbb{N}}$
. Given a tuple
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
of matrices, we define for each such
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
of matrices, we define for each such
![]() $\Gamma \subset J^{\mathbb{N}}$
and
$\Gamma \subset J^{\mathbb{N}}$
and
![]() $s \geqslant 0$
the pressure by setting
$s \geqslant 0$
the pressure by setting
The assumption
![]() $\sigma(\Gamma) \subset \Gamma$
guarantees that if
$\sigma(\Gamma) \subset \Gamma$
guarantees that if
![]() ${\texttt{i}} \in J^m$
and
${\texttt{i}} \in J^m$
and
![]() ${\texttt{j}} \in J^n$
such that
${\texttt{j}} \in J^n$
such that
![]() ${\texttt{i}}{\texttt{j}} \in \Gamma_{m+n}$
, then
${\texttt{i}}{\texttt{j}} \in \Gamma_{m+n}$
, then
![]() ${\texttt{i}} \in \Gamma_m$
and
${\texttt{i}} \in \Gamma_m$
and
![]() ${\texttt{j}} \in \Gamma_n$
. Therefore, as the singular value function is sub-multiplicative, the sequence
${\texttt{j}} \in \Gamma_n$
. Therefore, as the singular value function is sub-multiplicative, the sequence
![]() $(\log\sum_{{\texttt{i}} \in \Gamma_n} {\varphi}^s(A_{\texttt{i}}))_{n \in {\mathbb{N}}}$
is sub-additive and hence, the limit above exists or is
$(\log\sum_{{\texttt{i}} \in \Gamma_n} {\varphi}^s(A_{\texttt{i}}))_{n \in {\mathbb{N}}}$
is sub-additive and hence, the limit above exists or is
![]() $-\infty$
by Fekete’s lemma.
$-\infty$
by Fekete’s lemma.
Let
![]() ${\mathsf{A}}$
be a tuple of strictly contractive matrices and
${\mathsf{A}}$
be a tuple of strictly contractive matrices and
![]() $\Gamma \subset J^{\mathbb{N}}$
be a non-empty compact set such that
$\Gamma \subset J^{\mathbb{N}}$
be a non-empty compact set such that
![]() $\sigma(\Gamma) \subset \Gamma$
. Since
$\sigma(\Gamma) \subset \Gamma$
. Since
![]() ${\varphi}^s(A_i) \leqslant {\varphi}^t(A_i) \max_{k \in J}\|A_k\|^{(s-t)}$
for all
${\varphi}^s(A_i) \leqslant {\varphi}^t(A_i) \max_{k \in J}\|A_k\|^{(s-t)}$
for all
![]() $i \in J$
, we see that
$i \in J$
, we see that
![]() $P(\Gamma,{\mathsf{A}},s) \leqslant P(\Gamma,{\mathsf{A}},t) + (s-t) \log\max_{k \in J}\|A_k\|$
for all
$P(\Gamma,{\mathsf{A}},s) \leqslant P(\Gamma,{\mathsf{A}},t) + (s-t) \log\max_{k \in J}\|A_k\|$
for all
![]() $s \gt t \geqslant 0$
. Since
$s \gt t \geqslant 0$
. Since
![]() ${\mathsf{A}}$
consists only of strictly contractive matrices, we have
${\mathsf{A}}$
consists only of strictly contractive matrices, we have
![]() $\max_{k \in J}\|A_k\|\lt 1$
and hence, the pressure
$\max_{k \in J}\|A_k\|\lt 1$
and hence, the pressure
![]() $P(\Gamma,{\mathsf{A}},s)$
is strictly decreasing as a function of s whenever it is finite. Notice also that
$P(\Gamma,{\mathsf{A}},s)$
is strictly decreasing as a function of s whenever it is finite. Notice also that
![]() $P(\Gamma,{\mathsf{A}},0) = \lim_{n \to \infty} ({1}/{n}) \log \#\Gamma_n \geqslant 0$
and
$P(\Gamma,{\mathsf{A}},0) = \lim_{n \to \infty} ({1}/{n}) \log \#\Gamma_n \geqslant 0$
and
![]() $\lim_{s \to \infty} P(\Gamma,{\mathsf{A}},s) = -\infty$
. In this case, we define the affinity dimension by setting
$\lim_{s \to \infty} P(\Gamma,{\mathsf{A}},s) = -\infty$
. In this case, we define the affinity dimension by setting
Notice that if the pressure
![]() $s \mapsto P(\Gamma,{\mathsf{A}},s)$
is continuous at
$s \mapsto P(\Gamma,{\mathsf{A}},s)$
is continuous at
![]() $s_0 = {\textrm{dim}_{\textrm{aff}}}(\Gamma,{\mathsf{A}})$
, then
$s_0 = {\textrm{dim}_{\textrm{aff}}}(\Gamma,{\mathsf{A}})$
, then
![]() $P(\Gamma,{\mathsf{A}},s_0) = 0$
.
$P(\Gamma,{\mathsf{A}},s_0) = 0$
.
We are interested in the properties of the pressure
as a function of s and the affinity dimension
![]() ${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) = {\textrm{dim}_{\textrm{aff}}}(J^{\mathbb{N}},{\mathsf{A}})$
. To that end, let us introduce some further notation. Let
${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) = {\textrm{dim}_{\textrm{aff}}}(J^{\mathbb{N}},{\mathsf{A}})$
. To that end, let us introduce some further notation. Let
![]() $I = \{i \in J \,:\, A_i \text{ is invertible}\}$
. In this case, we trivially have that
$I = \{i \in J \,:\, A_i \text{ is invertible}\}$
. In this case, we trivially have that
is a compact subset of
![]() $J^{\mathbb{N}}$
and satisfies
$J^{\mathbb{N}}$
and satisfies
![]() $\sigma(I^{\mathbb{N}}) = I^{\mathbb{N}}$
. Therefore, the pressure
$\sigma(I^{\mathbb{N}}) = I^{\mathbb{N}}$
. Therefore, the pressure
![]() $P(I^{\mathbb{N}},{\mathsf{A}},s)$
is well-defined for all
$P(I^{\mathbb{N}},{\mathsf{A}},s)$
is well-defined for all
![]() $s \geqslant 0$
. We also define
$s \geqslant 0$
. We also define
It is easy to see that
![]() $\Sigma$
is a compact subset of
$\Sigma$
is a compact subset of
![]() $J^{\mathbb{N}}$
and satisfies
$J^{\mathbb{N}}$
and satisfies
![]() $\sigma(\Sigma) \subset \Sigma$
. Indeed, if
$\sigma(\Sigma) \subset \Sigma$
. Indeed, if
![]() ${\texttt{j}} \in \sigma(\Sigma)$
, then there is
${\texttt{j}} \in \sigma(\Sigma)$
, then there is
![]() ${\texttt{i}} \in \Sigma$
such that
${\texttt{i}} \in \Sigma$
such that
![]() ${\texttt{j}} = \sigma{\texttt{i}}$
and
${\texttt{j}} = \sigma{\texttt{i}}$
and
![]() $A_{{\texttt{i}}|_n} \ne 0$
for all
$A_{{\texttt{i}}|_n} \ne 0$
for all
![]() $n \in {\mathbb{N}}$
. As clearly
$n \in {\mathbb{N}}$
. As clearly
![]() $A_{\sigma{\texttt{i}}|_n} \ne 0$
for all
$A_{\sigma{\texttt{i}}|_n} \ne 0$
for all
![]() $n \in {\mathbb{N}}$
, we see that
$n \in {\mathbb{N}}$
, we see that
![]() ${\texttt{j}} = \sigma{\texttt{i}} \in \Sigma$
as claimed. Hence, also the pressure
${\texttt{j}} = \sigma{\texttt{i}} \in \Sigma$
as claimed. Hence, also the pressure
![]() $P(\Sigma,{\mathsf{A}},s)$
is well-defined for all
$P(\Sigma,{\mathsf{A}},s)$
is well-defined for all
![]() $s \geqslant 0$
. Observe that the inclusion
$s \geqslant 0$
. Observe that the inclusion
![]() $\sigma(\Sigma) \subset \Sigma$
can be strict: if
$\sigma(\Sigma) \subset \Sigma$
can be strict: if
![]() $J = \{0,1\}$
and
$J = \{0,1\}$
and
 \begin{equation*} A_0 = \begin{pmatrix} 0 & \quad 1 \\[4pt] 0 & \quad 0 \end{pmatrix}, \qquad A_1 = \begin{pmatrix} 0 & \quad 0 \\[4pt] 0 & \quad 1 \end{pmatrix},\end{equation*}
\begin{equation*} A_0 = \begin{pmatrix} 0 & \quad 1 \\[4pt] 0 & \quad 0 \end{pmatrix}, \qquad A_1 = \begin{pmatrix} 0 & \quad 0 \\[4pt] 0 & \quad 1 \end{pmatrix},\end{equation*}
then
![]() $\Sigma = \{0111\cdots, 111\cdots\}$
and
$\Sigma = \{0111\cdots, 111\cdots\}$
and
![]() $\sigma(\Sigma) = \{111\cdots\}$
.
$\sigma(\Sigma) = \{111\cdots\}$
.
Lemma 2·2. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
, then
$\max_{i \in J} \|A_i\| \lt 1$
, then
 \begin{equation*} P({\mathsf{A}},s) = \begin{cases} \log \# J, &\text{if } s = 0, \\[4pt] P(\Sigma,{\mathsf{A}},s), &\text{if } 0 \lt s \leqslant 1, \\[4pt] P(I^{\mathbb{N}},{\mathsf{A}},s), &\text{if } 1 \lt s \lt \infty. \end{cases} \end{equation*}
\begin{equation*} P({\mathsf{A}},s) = \begin{cases} \log \# J, &\text{if } s = 0, \\[4pt] P(\Sigma,{\mathsf{A}},s), &\text{if } 0 \lt s \leqslant 1, \\[4pt] P(I^{\mathbb{N}},{\mathsf{A}},s), &\text{if } 1 \lt s \lt \infty. \end{cases} \end{equation*}
Furthermore, the function
![]() $s \mapsto P({\mathsf{A}},s)$
is strictly decreasing on
$s \mapsto P({\mathsf{A}},s)$
is strictly decreasing on
![]() $[0,\infty)$
, continuous on (0, 1), and uniformly continuous on
$[0,\infty)$
, continuous on (0, 1), and uniformly continuous on
![]() $(1,\infty)$
whenever it is finite.
$(1,\infty)$
whenever it is finite.
Proof. Recall first that
![]() ${\varphi}^s(A) = \alpha_1(A)^s = \|A\|^s$
for all
${\varphi}^s(A) = \alpha_1(A)^s = \|A\|^s$
for all
![]() $0 \leqslant s \leqslant 1$
. Therefore, as we interpreted
$0 \leqslant s \leqslant 1$
. Therefore, as we interpreted
![]() $0^0=1$
, we have
$0^0=1$
, we have
Since
![]() $\alpha_1(A)\gt0$
if and only if
$\alpha_1(A)\gt0$
if and only if
![]() $A \in M_2({\mathbb{R}})$
is non-zero, we see that for each
$A \in M_2({\mathbb{R}})$
is non-zero, we see that for each
![]() $0 \lt s \leqslant 1$
the singular value function satisfies
$0 \lt s \leqslant 1$
the singular value function satisfies
![]() ${\varphi}^s(A_{\texttt{i}}) = \|A_{\texttt{i}}\|^s \gt 0$
if and only if
${\varphi}^s(A_{\texttt{i}}) = \|A_{\texttt{i}}\|^s \gt 0$
if and only if
![]() ${\texttt{i}} \in \Sigma_*$
. Therefore,
${\texttt{i}} \in \Sigma_*$
. Therefore,
![]() $P({\mathsf{A}},s) = P(\Sigma,{\mathsf{A}},s)$
for all
$P({\mathsf{A}},s) = P(\Sigma,{\mathsf{A}},s)$
for all
![]() $0 \lt s \leqslant 1$
. Furthermore, since
$0 \lt s \leqslant 1$
. Furthermore, since
![]() $\alpha_2(A)\gt0$
if and only if
$\alpha_2(A)\gt0$
if and only if
![]() $A \in GL_2({\mathbb{R}})$
, we have that for every
$A \in GL_2({\mathbb{R}})$
, we have that for every
![]() $1\lt s\lt \infty$
the singular value function satisfies
$1\lt s\lt \infty$
the singular value function satisfies
![]() ${\varphi}^s(A_{\texttt{i}})\gt0$
if and only if
${\varphi}^s(A_{\texttt{i}})\gt0$
if and only if
![]() ${\texttt{i}} \in I^*$
. This shows
${\texttt{i}} \in I^*$
. This shows
![]() $P({\mathsf{A}},s) = P(I^{\mathbb{N}},{\mathsf{A}},s)$
for all
$P({\mathsf{A}},s) = P(I^{\mathbb{N}},{\mathsf{A}},s)$
for all
![]() $1\lt s\lt \infty$
. The function
$1\lt s\lt \infty$
. The function
![]() $s \mapsto P({\mathsf{A}},s)$
has already seen strictly decreasing. The continuity on (0, 1) follows from [
Reference Feng and Shmerkin16
, theorem 1·2(3)] and the uniform continuity on
$s \mapsto P({\mathsf{A}},s)$
has already seen strictly decreasing. The continuity on (0, 1) follows from [
Reference Feng and Shmerkin16
, theorem 1·2(3)] and the uniform continuity on
![]() $(1,\infty)$
follows directly from [
Reference Käenmäki and Vilppolainen23
, lemma 2·1].
$(1,\infty)$
follows directly from [
Reference Käenmäki and Vilppolainen23
, lemma 2·1].
The following lemma characterises the continuity of the function
![]() $s \mapsto P({\mathsf{A}},s)$
at 0.
$s \mapsto P({\mathsf{A}},s)$
at 0.
Lemma 2·3. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
, then the function
$\max_{i \in J} \|A_i\| \lt 1$
, then the function
![]() $s \mapsto P({\mathsf{A}},s)$
is right-continuous at 0 if and only if the semigroup
$s \mapsto P({\mathsf{A}},s)$
is right-continuous at 0 if and only if the semigroup
![]() $\{A_{\texttt{i}} \,:\, {\texttt{i}} \in J^*\}$
does not contain rank zero matrices.
$\{A_{\texttt{i}} \,:\, {\texttt{i}} \in J^*\}$
does not contain rank zero matrices.
Proof. If the semigroup
![]() $\{A_{\texttt{i}} \,:\, {\texttt{i}} \in J^*\}$
does not contain rank zero matrices, then
$\{A_{\texttt{i}} \,:\, {\texttt{i}} \in J^*\}$
does not contain rank zero matrices, then
![]() $\Sigma = J^{\mathbb{N}}$
and the right-continuity at 0 is guaranteed by Lemma 2·2. If
$\Sigma = J^{\mathbb{N}}$
and the right-continuity at 0 is guaranteed by Lemma 2·2. If
![]() $A_{\texttt{i}}$
has rank zero for some
$A_{\texttt{i}}$
has rank zero for some
![]() ${\texttt{i}} \in J^n$
and
${\texttt{i}} \in J^n$
and
![]() $n \in {\mathbb{N}}$
, then clearly
$n \in {\mathbb{N}}$
, then clearly
![]() $\# \Sigma_n \lt \# J^n = (\# J)^n$
. Fix
$\# \Sigma_n \lt \# J^n = (\# J)^n$
. Fix
![]() $0 \lt s \leqslant 1$
and notice that Lemma 2·2 implies
$0 \lt s \leqslant 1$
and notice that Lemma 2·2 implies
and
where the limit exists by Lemma 2·2. In particular, the function
![]() $s \mapsto P({\mathsf{A}},s)$
is not right-continuous at 0.
$s \mapsto P({\mathsf{A}},s)$
is not right-continuous at 0.
The possible discontinuity at 1 has already been observed by Feng and Shmerkin [
Reference Feng and Shmerkin16
, remark 1·1]. In their example, the pressure is not finite when
![]() $s \gt 1$
, but it is easy to see that this is not a necessity. If
$s \gt 1$
, but it is easy to see that this is not a necessity. If
![]() $J = \{0,1\}$
and
$J = \{0,1\}$
and
 \begin{equation*} A_0 = \begin{pmatrix} 1 & 0 \\[4pt] 0 & 0 \end{pmatrix}, \qquad A_1 = \begin{pmatrix} 1 & 0 \\[4pt] 0 & 1 \end{pmatrix},\end{equation*}
\begin{equation*} A_0 = \begin{pmatrix} 1 & 0 \\[4pt] 0 & 0 \end{pmatrix}, \qquad A_1 = \begin{pmatrix} 1 & 0 \\[4pt] 0 & 1 \end{pmatrix},\end{equation*}
then, by lemma 2·2, for
![]() ${\mathsf{A}} = (A_0,A_1) \in M_2({\mathbb{R}})^J$
we have
${\mathsf{A}} = (A_0,A_1) \in M_2({\mathbb{R}})^J$
we have
![]() $P({\mathsf{A}},1) = \log 2$
and
$P({\mathsf{A}},1) = \log 2$
and
![]() $P({\mathsf{A}},s) = 0$
for all
$P({\mathsf{A}},s) = 0$
for all
![]() $s\gt1$
. The continuity of the function
$s\gt1$
. The continuity of the function
![]() $s \mapsto P({\mathsf{A}},s)$
at 1 will be characterised for dominated and irreducible tuples in Lemma 2·10.
$s \mapsto P({\mathsf{A}},s)$
at 1 will be characterised for dominated and irreducible tuples in Lemma 2·10.
Let us next determine when the pressure is finite. For that, we need the following definition. Given a tuple
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
of matrices, we define the joint spectral radius by setting
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
of matrices, we define the joint spectral radius by setting
As the operator norm is sub-multiplicative, the sequence
![]() $(\log \max_{{\texttt{i}} \in J^n} \|A_{\texttt{i}}\|)_{n \in {\mathbb{N}}}$
is sub-additive and hence, the limit above exists by Fekete’s lemma.
$(\log \max_{{\texttt{i}} \in J^n} \|A_{\texttt{i}}\|)_{n \in {\mathbb{N}}}$
is sub-additive and hence, the limit above exists by Fekete’s lemma.
Lemma 2·4. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
is dominated or irreducible, then
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
is dominated or irreducible, then
![]() ${\varrho}({\mathsf{A}}) \gt 0$
.
${\varrho}({\mathsf{A}}) \gt 0$
.
Proof. Let us first assume that
![]() ${\mathsf{A}}$
is dominated and
${\mathsf{A}}$
is dominated and
![]() ${\mathcal{C}} \subset {\mathbb{RP}^{1}}$
is a strongly invariant multicone for
${\mathcal{C}} \subset {\mathbb{RP}^{1}}$
is a strongly invariant multicone for
![]() ${\mathsf{A}}$
. Since there exists a multicone
${\mathsf{A}}$
. Since there exists a multicone
![]() ${\mathcal{C}}_0 \subset {\mathbb{RP}^{1}}$
such that
${\mathcal{C}}_0 \subset {\mathbb{RP}^{1}}$
such that
![]() $\bigcup_{{\texttt{i}} \in J^n} A_{\texttt{i}} {\mathcal{C}} \subset \bigcup_{i \in J} A_i {\mathcal{C}} \subset {\mathcal{C}}_0 \subset {\mathcal{C}}^o$
for all
$\bigcup_{{\texttt{i}} \in J^n} A_{\texttt{i}} {\mathcal{C}} \subset \bigcup_{i \in J} A_i {\mathcal{C}} \subset {\mathcal{C}}_0 \subset {\mathcal{C}}^o$
for all
![]() $n \in {\mathbb{N}}$
, we find, by applying [
Reference Bochi and Morris8
, lemma 2·2], a constant
$n \in {\mathbb{N}}$
, we find, by applying [
Reference Bochi and Morris8
, lemma 2·2], a constant
![]() $\kappa \gt 0$
such that
$\kappa \gt 0$
such that
for all
![]() $V \in {\mathcal{C}}_0$
and
$V \in {\mathcal{C}}_0$
and
![]() ${\texttt{i}} \in J^*$
. It follows that if
${\texttt{i}} \in J^*$
. It follows that if
![]() $V \in {\mathcal{C}}_0$
, then
$V \in {\mathcal{C}}_0$
, then
![]() $A_{\texttt{j}} V \in {\mathcal{C}}_0$
and
$A_{\texttt{j}} V \in {\mathcal{C}}_0$
and
![]() $\|A_{\texttt{i}} A_{\texttt{j}}\| \geqslant \|A_{\texttt{i}} A_{\texttt{j}} | V\| = \|A_{\texttt{i}}|A_{\texttt{j}} V\| \|A_{\texttt{j}}|V\| \geqslant \kappa^2\|A_{\texttt{i}}\|\|A_{\texttt{j}}\|$
for all
$\|A_{\texttt{i}} A_{\texttt{j}}\| \geqslant \|A_{\texttt{i}} A_{\texttt{j}} | V\| = \|A_{\texttt{i}}|A_{\texttt{j}} V\| \|A_{\texttt{j}}|V\| \geqslant \kappa^2\|A_{\texttt{i}}\|\|A_{\texttt{j}}\|$
for all
![]() ${\texttt{i}},{\texttt{j}} \in J^*$
. Therefore,
${\texttt{i}},{\texttt{j}} \in J^*$
. Therefore,
as claimed.
Although the proof in the irreducible case can be found in [
Reference Jungers19
, lemma 2·2], we present the full details for the convenience of the reader. Denote the unit circle by
![]() $S^1$
and suppose that for each
$S^1$
and suppose that for each
![]() $k \in {\mathbb{N}}$
there is
$k \in {\mathbb{N}}$
there is
![]() $x_k \in S^1$
such that for every
$x_k \in S^1$
such that for every
![]() $i \in J$
we have
$i \in J$
we have
![]() $|A_ix_k| \lt {1}/{k}$
. By the compactness of
$|A_ix_k| \lt {1}/{k}$
. By the compactness of
![]() $S^1$
, there is
$S^1$
, there is
![]() $x \in S^1$
such that
$x \in S^1$
such that
![]() $|A_ix|=0$
for all
$|A_ix|=0$
for all
![]() $i \in J$
. Choosing
$i \in J$
. Choosing
![]() $V = {\textrm{span}}(x) \in {\mathbb{RP}^{1}}$
, we see that
$V = {\textrm{span}}(x) \in {\mathbb{RP}^{1}}$
, we see that
![]() $A_iV = \{(0,0)\} \subset V$
for all
$A_iV = \{(0,0)\} \subset V$
for all
![]() $i \in J$
and
$i \in J$
and
![]() ${\mathsf{A}}$
is reducible.
${\mathsf{A}}$
is reducible.
It follows that there is
![]() $\delta \gt 0$
such that for every
$\delta \gt 0$
such that for every
![]() $x \in S^1$
there exists
$x \in S^1$
there exists
![]() $i \in J$
for which
$i \in J$
for which
![]() $|A_ix| \geqslant \delta$
. Let us next apply this inductively. Fix
$|A_ix| \geqslant \delta$
. Let us next apply this inductively. Fix
![]() $x_0 \in S^1$
and choose
$x_0 \in S^1$
and choose
![]() $i_1 \in J$
such that
$i_1 \in J$
such that
![]() $|A_{i_1}x_0| \geqslant \delta$
. Write
$|A_{i_1}x_0| \geqslant \delta$
. Write
![]() $x_1 = A_{i_1}x_0$
and choose
$x_1 = A_{i_1}x_0$
and choose
![]() $i_2 \in J$
such that
$i_2 \in J$
such that
![]() $|A_{i_2}({x_1}/{|x_1|})| \geqslant \delta$
whence
$|A_{i_2}({x_1}/{|x_1|})| \geqslant \delta$
whence
![]() $|A_{i_2}A_{i_1}x_0| = |A_{i_2}x_1| \geqslant \delta|x_1| = \delta|A_{i_1}x_0| \geqslant \delta^2$
. Continuing in this manner, we find for each
$|A_{i_2}A_{i_1}x_0| = |A_{i_2}x_1| \geqslant \delta|x_1| = \delta|A_{i_1}x_0| \geqslant \delta^2$
. Continuing in this manner, we find for each
![]() $n \in {\mathbb{N}}$
a word
$n \in {\mathbb{N}}$
a word
![]() ${\texttt{i}}_n \in J^n$
such that
${\texttt{i}}_n \in J^n$
such that
![]() $\|A_{{\texttt{i}}_n}\| \geqslant |A_{{\texttt{i}}_n} x_0| \geqslant \delta^n$
. Hence,
$\|A_{{\texttt{i}}_n}\| \geqslant |A_{{\texttt{i}}_n} x_0| \geqslant \delta^n$
. Hence,
as wished.
The following two lemmas characterise the finiteness of the pressure.
Lemma 2·5. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
, then the following five conditions are equivalent:
$\max_{i \in J} \|A_i\| \lt 1$
, then the following five conditions are equivalent:
-
(i)
 $P({\mathsf{A}},s) \gt -\infty$
for all
$P({\mathsf{A}},s) \gt -\infty$
for all
 $0 \leqslant s \leqslant 1$
;
$0 \leqslant s \leqslant 1$
; -
(ii)
 $\lim_{s \downarrow 0} P({\mathsf{A}},s) \gt -\infty$
;
$\lim_{s \downarrow 0} P({\mathsf{A}},s) \gt -\infty$
; -
(iii) there does not exist
 $n \in {\mathbb{N}}$
such that
$n \in {\mathbb{N}}$
such that
 $A_{\texttt{i}} = 0$
for all
$A_{\texttt{i}} = 0$
for all
 ${\texttt{i}} \in J^n$
;
${\texttt{i}} \in J^n$
; -
(iv) there exists
 ${\texttt{j}} \in J^{\mathbb{N}}$
such that
${\texttt{j}} \in J^{\mathbb{N}}$
such that
 $A_{{\texttt{j}}|_n} \ne 0$
for all
$A_{{\texttt{j}}|_n} \ne 0$
for all
 $n \in {\mathbb{N}}$
;
$n \in {\mathbb{N}}$
; -
(v)
 ${\varrho}({\mathsf{A}})\gt0$
.
${\varrho}({\mathsf{A}})\gt0$
.
Furthermore, all of these conditions hold if
![]() ${\mathsf{A}}$
is dominated or irreducible.
${\mathsf{A}}$
is dominated or irreducible.
Proof. Notice that the limit in (ii) exists by Lemma 2·2 and the implications (i)
![]() $\Rightarrow$
(ii) and (iv)
$\Rightarrow$
(ii) and (iv)
![]() $\Rightarrow$
(iii) are trivial. Let us first show the implication (ii)
$\Rightarrow$
(iii) are trivial. Let us first show the implication (ii)
![]() $\Rightarrow$
(iii). If (iii) does not hold, then there exists
$\Rightarrow$
(iii). If (iii) does not hold, then there exists
![]() $n_0 \in {\mathbb{N}}$
such that
$n_0 \in {\mathbb{N}}$
such that
![]() $A_{\texttt{i}} = 0$
for all
$A_{\texttt{i}} = 0$
for all
![]() ${\texttt{i}} \in J^{n_0}$
. Since now
${\texttt{i}} \in J^{n_0}$
. Since now
![]() $\|A_{\texttt{i}}\| = 0$
for all
$\|A_{\texttt{i}}\| = 0$
for all
![]() ${\texttt{i}} \in J^n$
and
${\texttt{i}} \in J^n$
and
![]() $n \geqslant n_0$
, we see that
$n \geqslant n_0$
, we see that
![]() $P({\mathsf{A}},s) = -\infty$
for all
$P({\mathsf{A}},s) = -\infty$
for all
![]() $s\gt0$
and (ii) cannot hold.
$s\gt0$
and (ii) cannot hold.
Let us then show the implication (iii)
![]() $\Rightarrow$
(iv). If (iv) does not hold, then for every
$\Rightarrow$
(iv). If (iv) does not hold, then for every
![]() ${\texttt{j}} \in J^{\mathbb{N}}$
there is
${\texttt{j}} \in J^{\mathbb{N}}$
there is
![]() $n({\texttt{j}}) \in {\mathbb{N}}$
such that
$n({\texttt{j}}) \in {\mathbb{N}}$
such that
![]() $A_{{\texttt{j}}|_{n({\texttt{j}})}} = 0$
. By compactness of
$A_{{\texttt{j}}|_{n({\texttt{j}})}} = 0$
. By compactness of
![]() $J^{\mathbb{N}}$
, there exist
$J^{\mathbb{N}}$
, there exist
![]() $M \in {\mathbb{N}}$
and
$M \in {\mathbb{N}}$
and
![]() ${\texttt{j}}_1,\ldots,{\texttt{j}}_M \in J^{\mathbb{N}}$
such that
${\texttt{j}}_1,\ldots,{\texttt{j}}_M \in J^{\mathbb{N}}$
such that
![]() $\{[{\texttt{j}}_i|_{n({\texttt{j}}_i)}]\}_{i=1}^M$
still covers
$\{[{\texttt{j}}_i|_{n({\texttt{j}}_i)}]\}_{i=1}^M$
still covers
![]() $J^{\mathbb{N}}$
. Choosing
$J^{\mathbb{N}}$
. Choosing
![]() $n = \max_{i \in \{1,\ldots,M\}} n({\texttt{j}}_i)$
, we see that for every
$n = \max_{i \in \{1,\ldots,M\}} n({\texttt{j}}_i)$
, we see that for every
![]() ${\texttt{i}} \in J^n$
there is
${\texttt{i}} \in J^n$
there is
![]() $i \in \{1,\ldots,M\}$
such that
$i \in \{1,\ldots,M\}$
such that
![]() $A_{\texttt{i}} = A_{{\texttt{j}}_i|_{n({\texttt{j}}_i)}}A_{\sigma^{n({\texttt{j}}_i)}{\texttt{i}}} = 0$
and (iii) cannot hold.
$A_{\texttt{i}} = A_{{\texttt{j}}_i|_{n({\texttt{j}}_i)}}A_{\sigma^{n({\texttt{j}}_i)}{\texttt{i}}} = 0$
and (iii) cannot hold.
Since
![]() ${\mathsf{A}}$
is a tuple of strictly contractive matrices, the function
${\mathsf{A}}$
is a tuple of strictly contractive matrices, the function
![]() $s \mapsto P({\mathsf{A}},s)$
is strictly decreasing whenever it is finite. Therefore, we have
$s \mapsto P({\mathsf{A}},s)$
is strictly decreasing whenever it is finite. Therefore, we have
![]() $P({\mathsf{A}},s) \geqslant P({\mathsf{A}},1) \geqslant \log {\varrho}({\mathsf{A}})$
for all
$P({\mathsf{A}},s) \geqslant P({\mathsf{A}},1) \geqslant \log {\varrho}({\mathsf{A}})$
for all
![]() $0 \leqslant s \leqslant 1$
and hence, we have the implication (v)
$0 \leqslant s \leqslant 1$
and hence, we have the implication (v)
![]() $\Rightarrow$
(i). Therefore, to conclude the proof, it suffices to show the implication (iii)
$\Rightarrow$
(i). Therefore, to conclude the proof, it suffices to show the implication (iii)
![]() $\Rightarrow$
(v) and also verify condition (v) when
$\Rightarrow$
(v) and also verify condition (v) when
![]() ${\mathsf{A}}$
is dominated or irreducible. While the latter is immediately assured by Lemma 2·4, we also see that to prove the former, we may assume that
${\mathsf{A}}$
is dominated or irreducible. While the latter is immediately assured by Lemma 2·4, we also see that to prove the former, we may assume that
![]() ${\mathsf{A}}$
is reducible. This means that, after possibly a change of basis, the matrices
${\mathsf{A}}$
is reducible. This means that, after possibly a change of basis, the matrices
![]() $A_i$
in
$A_i$
in
![]() ${\mathsf{A}}$
are of the form
${\mathsf{A}}$
are of the form
 \begin{equation*} A_i = \begin{pmatrix} a_i & b_i \\[4pt] 0 & c_i \end{pmatrix} \end{equation*}
\begin{equation*} A_i = \begin{pmatrix} a_i & b_i \\[4pt] 0 & c_i \end{pmatrix} \end{equation*}
for all
![]() $i \in J$
. Since
$i \in J$
. Since
![]() $A_i(1,0) = a_i(1,0)$
and
$A_i(1,0) = a_i(1,0)$
and
![]() $A_i(({b_i}/({c_i-a_i})),1) = c_i(({b_i}/({c_i-a_i})),1)$
when
$A_i(({b_i}/({c_i-a_i})),1) = c_i(({b_i}/({c_i-a_i})),1)$
when
![]() $a_i \ne c_i$
, we see that
$a_i \ne c_i$
, we see that
![]() $\max\{|a_i|,|c_i|\} \leqslant \|A_i\|$
for all
$\max\{|a_i|,|c_i|\} \leqslant \|A_i\|$
for all
![]() $i \in J$
. As the product of upper triangular matrices is upper triangular with diagonal entries obtained as products of the corresponding diagonal entries, we also have
$i \in J$
. As the product of upper triangular matrices is upper triangular with diagonal entries obtained as products of the corresponding diagonal entries, we also have
![]() $\max\{|a_{i_1} \cdots a_{i_n}|, |c_{i_1} \cdots c_{i_n}|\} \leqslant \|A_{\texttt{i}}\|$
for all
$\max\{|a_{i_1} \cdots a_{i_n}|, |c_{i_1} \cdots c_{i_n}|\} \leqslant \|A_{\texttt{i}}\|$
for all
![]() ${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
![]() $n \in {\mathbb{N}}$
. Therefore, if condition (v) does not hold i.e.
$n \in {\mathbb{N}}$
. Therefore, if condition (v) does not hold i.e.
![]() ${\varrho}({\mathsf{A}}) = 0$
, then
${\varrho}({\mathsf{A}}) = 0$
, then
and, similarly,
![]() $\max_{i \in J} |c_i| = 0$
. In other words, the diagonal entries in all of the matrices
$\max_{i \in J} |c_i| = 0$
. In other words, the diagonal entries in all of the matrices
![]() $A_i$
are zero. Thus,
$A_i$
are zero. Thus,
![]() $A_{\texttt{i}} = 0$
for all
$A_{\texttt{i}} = 0$
for all
![]() ${\texttt{i}} \in J^2$
and condition (iii) does not hold.
${\texttt{i}} \in J^2$
and condition (iii) does not hold.
Lemma 2·6. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
, then the following five conditions are equivalent:
$\max_{i \in J} \|A_i\| \lt 1$
, then the following five conditions are equivalent:
-
(i)
 $P(I^{\mathbb{N}},{\mathsf{A}},s) \gt -\infty$
for all
$P(I^{\mathbb{N}},{\mathsf{A}},s) \gt -\infty$
for all
 $s \geqslant 0$
;
$s \geqslant 0$
; -
(ii)
 $P({\mathsf{A}},s) \gt -\infty$
for all
$P({\mathsf{A}},s) \gt -\infty$
for all
 $s \geqslant 0$
;
$s \geqslant 0$
; -
(iii)
 $\lim_{s \downarrow 1} P({\mathsf{A}},s) \gt -\infty$
;
$\lim_{s \downarrow 1} P({\mathsf{A}},s) \gt -\infty$
; -
(iv) there does not exist
 $n \in {\mathbb{N}}$
such that
$n \in {\mathbb{N}}$
such that
 $A_{\texttt{i}}$
has rank at most one for all
$A_{\texttt{i}}$
has rank at most one for all
 ${\texttt{i}} \in J^n$
;
${\texttt{i}} \in J^n$
; -
(v) there exists
 $j \in J$
such that
$j \in J$
such that
 $A_j \in GL_2({\mathbb{R}})$
.
$A_j \in GL_2({\mathbb{R}})$
.
Proof. Notice that the limit in (iii) exists by Lemma 2·2 and the implications (i)
![]() $\Rightarrow$
(ii) and (ii)
$\Rightarrow$
(ii) and (ii)
![]() $\Rightarrow$
(iii) are trivial. Let us first show the implication (iii)
$\Rightarrow$
(iii) are trivial. Let us first show the implication (iii)
![]() $\Rightarrow$
(iv). If (iv) does not hold, then there exists
$\Rightarrow$
(iv). If (iv) does not hold, then there exists
![]() $n_0 \in {\mathbb{N}}$
such that
$n_0 \in {\mathbb{N}}$
such that
![]() $A_{\texttt{i}}$
has rank at most one for all
$A_{\texttt{i}}$
has rank at most one for all
![]() ${\texttt{i}} \in J^{n_0}$
. It follows that for every
${\texttt{i}} \in J^{n_0}$
. It follows that for every
![]() ${\texttt{i}} \in J^n$
and
${\texttt{i}} \in J^n$
and
![]() $n \geqslant n_0$
the rank of
$n \geqslant n_0$
the rank of
![]() $A_{\texttt{i}}$
is at most one as it is bounded above by the rank of
$A_{\texttt{i}}$
is at most one as it is bounded above by the rank of
![]() $A_{{\texttt{i}}|_{n_0}}$
. Therefore, as
$A_{{\texttt{i}}|_{n_0}}$
. Therefore, as
![]() ${\varphi}^s(A_{\texttt{i}}) = 0$
for all
${\varphi}^s(A_{\texttt{i}}) = 0$
for all
![]() ${\texttt{i}} \in J^n$
,
${\texttt{i}} \in J^n$
,
![]() $n \geqslant n_0$
, and
$n \geqslant n_0$
, and
![]() $s\gt1$
, we have
$s\gt1$
, we have
![]() $P({\mathsf{A}},s) = -\infty$
for all
$P({\mathsf{A}},s) = -\infty$
for all
![]() $s\gt1$
and (iii) cannot hold.
$s\gt1$
and (iii) cannot hold.
Let us then show the implication (iv)
![]() $\Rightarrow$
(v). If (v) does not hold, then
$\Rightarrow$
(v). If (v) does not hold, then
![]() $A_j$
has rank at most one for all
$A_j$
has rank at most one for all
![]() $j \in J$
. It follows that for every
$j \in J$
. It follows that for every
![]() ${\texttt{i}} \in J^n$
and
${\texttt{i}} \in J^n$
and
![]() $n \in {\mathbb{N}}$
the rank of
$n \in {\mathbb{N}}$
the rank of
![]() $A_{\texttt{i}}$
is at most one and (iv) cannot hold.
$A_{\texttt{i}}$
is at most one and (iv) cannot hold.
Finally, let us show the implication (v)
![]() $\Rightarrow$
(i). The condition (v) implies that
$\Rightarrow$
(i). The condition (v) implies that
![]() $A_{{\texttt{j}}|_n} \in GL_2({\mathbb{R}})$
for all
$A_{{\texttt{j}}|_n} \in GL_2({\mathbb{R}})$
for all
![]() $n \in {\mathbb{N}}$
where
$n \in {\mathbb{N}}$
where
![]() ${\texttt{j}} = jj\cdots \in J^{\mathbb{N}}$
. Since
${\texttt{j}} = jj\cdots \in J^{\mathbb{N}}$
. Since
![]() ${\varphi}^s(A_{{\texttt{j}}|_n}) \geqslant \alpha_2(A_{{\texttt{j}}|_n}) \geqslant \alpha_2(A_j)^n \gt 0$
for all
${\varphi}^s(A_{{\texttt{j}}|_n}) \geqslant \alpha_2(A_{{\texttt{j}}|_n}) \geqslant \alpha_2(A_j)^n \gt 0$
for all
![]() $n \in {\mathbb{N}}$
and
$n \in {\mathbb{N}}$
and
![]() $s \geqslant 0$
, we see that
$s \geqslant 0$
, we see that
![]() $P(I^{\mathbb{N}},{\mathsf{A}},s) \geqslant \log\alpha_2(A_j) \gt -\infty$
for all
$P(I^{\mathbb{N}},{\mathsf{A}},s) \geqslant \log\alpha_2(A_j) \gt -\infty$
for all
![]() $s \geqslant 0$
as wished.
$s \geqslant 0$
as wished.
2·3. Equilibrium states
Let
![]() ${\mathcal{M}}_\sigma(J^{\mathbb{N}})$
be the collection of all
${\mathcal{M}}_\sigma(J^{\mathbb{N}})$
be the collection of all
![]() $\sigma$
-invariant Borel probability measures on
$\sigma$
-invariant Borel probability measures on
![]() $J^{\mathbb{N}}$
. If
$J^{\mathbb{N}}$
. If
![]() $0 \lt s \leqslant 1$
, then we say that a measure
$0 \lt s \leqslant 1$
, then we say that a measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is s-Gibbs-type if there exists a constant
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is s-Gibbs-type if there exists a constant
![]() $C \geqslant 1$
such that
$C \geqslant 1$
such that
for all
![]() ${\texttt{i}} \in J^n$
and
${\texttt{i}} \in J^n$
and
![]() $n \in {\mathbb{N}}$
.
$n \in {\mathbb{N}}$
.
Lemma 2·7. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
and is dominated or irreducible, then for every
$\max_{i \in J} \|A_i\| \lt 1$
and is dominated or irreducible, then for every
![]() $0 \lt s \leqslant 1$
there exist a unique ergodic s-Gibbs-type measure
$0 \lt s \leqslant 1$
there exist a unique ergodic s-Gibbs-type measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
.
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
.
Proof. Recall first that, by Lemma 2·5, the pressure
![]() $P({\mathsf{A}},s)$
is finite for all
$P({\mathsf{A}},s)$
is finite for all
![]() $0 \lt s \leqslant 1$
. If
$0 \lt s \leqslant 1$
. If
![]() ${\mathsf{A}}$
is irreducible, then the existence of the claimed measure
${\mathsf{A}}$
is irreducible, then the existence of the claimed measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
follows immediately from [
Reference Feng and Käenmäki15
, proposition 1·2]. We may thus assume that
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
follows immediately from [
Reference Feng and Käenmäki15
, proposition 1·2]. We may thus assume that
![]() ${\mathsf{A}}$
is dominated. Fix
${\mathsf{A}}$
is dominated. Fix
![]() $0 \lt s \leqslant 1$
and notice that, by (2), there exist
$0 \lt s \leqslant 1$
and notice that, by (2), there exist
![]() $\kappa \gt 0$
and a multicone
$\kappa \gt 0$
and a multicone
![]() ${\mathcal{C}}_0 \subset {\mathbb{RP}^{1}}$
such that
${\mathcal{C}}_0 \subset {\mathbb{RP}^{1}}$
such that
![]() $\|A_{\texttt{i}}|V\| \geqslant \kappa\|A_{\texttt{i}}\|$
for all
$\|A_{\texttt{i}}|V\| \geqslant \kappa\|A_{\texttt{i}}\|$
for all
![]() $V \in {\mathcal{C}}_0$
and
$V \in {\mathcal{C}}_0$
and
![]() ${\texttt{i}} \in J^*$
. Fixing
${\texttt{i}} \in J^*$
. Fixing
![]() $V \in {\mathcal{C}}_0$
, we see that
$V \in {\mathcal{C}}_0$
, we see that
 \begin{equation*} \log\|A_{{\texttt{i}}|_n}\|^s + \log\kappa^s \leqslant \sum_{k=0}^{n-1} \log\|A_{\sigma^k {\texttt{i}}|_1}|A_{\sigma{\texttt{i}}}V\|^s \leqslant \log\|A_{{\texttt{i}}|_n}\|^s \end{equation*}
\begin{equation*} \log\|A_{{\texttt{i}}|_n}\|^s + \log\kappa^s \leqslant \sum_{k=0}^{n-1} \log\|A_{\sigma^k {\texttt{i}}|_1}|A_{\sigma{\texttt{i}}}V\|^s \leqslant \log\|A_{{\texttt{i}}|_n}\|^s \end{equation*}
for all
![]() ${\texttt{i}} \in J^{\mathbb{N}}$
and
${\texttt{i}} \in J^{\mathbb{N}}$
and
![]() $n \in {\mathbb{N}}$
. By [
Reference Bowen10
, theorems 1·7 and 1·16], there exist an ergodic measure
$n \in {\mathbb{N}}$
. By [
Reference Bowen10
, theorems 1·7 and 1·16], there exist an ergodic measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
and a constant
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
and a constant
![]() $C \geqslant 1$
such that
$C \geqslant 1$
such that
for all
![]() ${\texttt{i}} \in J^n$
and
${\texttt{i}} \in J^n$
and
![]() $n \in {\mathbb{N}}$
; see also [
Reference Bárány, Käenmäki and Yu4
, lemma 2·12]. The uniqueness of
$n \in {\mathbb{N}}$
; see also [
Reference Bárány, Käenmäki and Yu4
, lemma 2·12]. The uniqueness of
![]() $\mu_K$
is now evident as two different ergodic measures are mutually singular.
$\mu_K$
is now evident as two different ergodic measures are mutually singular.
If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
is dominated, then it follows from (2) that
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
is dominated, then it follows from (2) that
![]() $\|A_{\texttt{i}}\| \geqslant \kappa^{2(n-1)}\|A_{i_1}\| \cdots \|A_{i_n}\| \geqslant \kappa^{2(n-1)}\min_{i \in J}\|A_i\|^n \gt 0$
for all
$\|A_{\texttt{i}}\| \geqslant \kappa^{2(n-1)}\|A_{i_1}\| \cdots \|A_{i_n}\| \geqslant \kappa^{2(n-1)}\min_{i \in J}\|A_i\|^n \gt 0$
for all
![]() ${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
![]() $n \in {\mathbb{N}}$
. Hence the semigroup
$n \in {\mathbb{N}}$
. Hence the semigroup
![]() $\{A_{\texttt{i}} \,:\, {\texttt{i}} \in J^*\}$
does not contain rank zero matrices and, by Lemma 2·3, the function
$\{A_{\texttt{i}} \,:\, {\texttt{i}} \in J^*\}$
does not contain rank zero matrices and, by Lemma 2·3, the function
![]() $s \mapsto P({\mathsf{A}},s)$
is right-continuous at 0. Furthermore, if there are no rank zero matrices, then
$s \mapsto P({\mathsf{A}},s)$
is right-continuous at 0. Furthermore, if there are no rank zero matrices, then
![]() $\Sigma = J^{\mathbb{N}}$
and the s-Gibbs-type measure
$\Sigma = J^{\mathbb{N}}$
and the s-Gibbs-type measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is fully supported on
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is fully supported on
![]() $J^{\mathbb{N}}$
. If
$J^{\mathbb{N}}$
. If
![]() ${\mathsf{A}}$
is irreducible, then
${\mathsf{A}}$
is irreducible, then
![]() $\mu_K$
is supported only on
$\mu_K$
is supported only on
![]() $\Sigma$
.
$\Sigma$
.
Given
![]() $\mu \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
and
$\mu \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
and
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
, we define for each
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
, we define for each
![]() $s \geqslant 0$
the energy by setting
$s \geqslant 0$
the energy by setting
The limit above exists or is
![]() $-\infty$
again by Fekete’s lemma. Recall that the entropy of
$-\infty$
again by Fekete’s lemma. Recall that the entropy of
![]() $\mu$
is
$\mu$
is
It is well known that
for all
![]() $\mu \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
and
$\mu \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
and
![]() $s \geqslant 0$
; for example, see [
Reference Käenmäki and Vilppolainen23
, section 3]. A measure
$s \geqslant 0$
; for example, see [
Reference Käenmäki and Vilppolainen23
, section 3]. A measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is an s-equilibrium state if it satisfies
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is an s-equilibrium state if it satisfies
The following lemma shows the uniqueness of the equilibrium state in dominated and irreducible cases.
Lemma 2·8. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
and is dominated or irreducible, then for every
$\max_{i \in J} \|A_i\| \lt 1$
and is dominated or irreducible, then for every
![]() $0 \lt s \leqslant 1$
the ergodic s-Gibbs-type measure
$0 \lt s \leqslant 1$
the ergodic s-Gibbs-type measure
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is the unique s-equilibrium state.
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
is the unique s-equilibrium state.
Proof. Fix
![]() $0 \lt s \leqslant 1$
and let
$0 \lt s \leqslant 1$
and let
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
be the ergodic s-Gibbs-type measure. Since, by Lemmas 2·7 and 2·5,
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
be the ergodic s-Gibbs-type measure. Since, by Lemmas 2·7 and 2·5,
 \begin{align*} h(\mu_K) + \Lambda(\mu_K,{\mathsf{A}},s) &= \lim_{n \to \infty} \frac{1}{n} \sum_{{\texttt{i}} \in \Sigma_n} \mu_K([{\texttt{i}}]) \log \frac{\|A_{\texttt{i}}\|^s}{\mu_K([{\texttt{i}}])} \\[4pt] &= \lim_{n \to \infty} \frac{1}{n} \sum_{{\texttt{i}} \in \Sigma_n} \mu_K([{\texttt{i}}]) \log e^{nP({\mathsf{A}},s)} = P({\mathsf{A}},s) \gt -\infty, \end{align*}
\begin{align*} h(\mu_K) + \Lambda(\mu_K,{\mathsf{A}},s) &= \lim_{n \to \infty} \frac{1}{n} \sum_{{\texttt{i}} \in \Sigma_n} \mu_K([{\texttt{i}}]) \log \frac{\|A_{\texttt{i}}\|^s}{\mu_K([{\texttt{i}}])} \\[4pt] &= \lim_{n \to \infty} \frac{1}{n} \sum_{{\texttt{i}} \in \Sigma_n} \mu_K([{\texttt{i}}]) \log e^{nP({\mathsf{A}},s)} = P({\mathsf{A}},s) \gt -\infty, \end{align*}
we see that
![]() $\mu_K$
is an s-equilibrium state. As
$\mu_K$
is an s-equilibrium state. As
![]() $\mu_K$
is ergodic, the uniqueness follows from [
Reference Käenmäki and Vilppolainen23
, theorem 3·6].
$\mu_K$
is ergodic, the uniqueness follows from [
Reference Käenmäki and Vilppolainen23
, theorem 3·6].
If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
contains an invertible matrix, then
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
contains an invertible matrix, then
![]() $I \ne \emptyset$
and, by Lemma 2·6,
$I \ne \emptyset$
and, by Lemma 2·6,
![]() $P(I^{\mathbb{N}},{\mathsf{A}},s) \gt -\infty$
for all
$P(I^{\mathbb{N}},{\mathsf{A}},s) \gt -\infty$
for all
![]() $s \geqslant 0$
. In this case, regardless of domination and irreducibility, it follows from [
Reference Käenmäki20
, Theorem 4·1] that for every
$s \geqslant 0$
. In this case, regardless of domination and irreducibility, it follows from [
Reference Käenmäki20
, Theorem 4·1] that for every
![]() $s \gt 0$
there exists an ergodic measure
$s \gt 0$
there exists an ergodic measure
![]() $\nu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
supported on
$\nu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
supported on
![]() $I^{\mathbb{N}}$
such that
$I^{\mathbb{N}}$
such that
Note that such a measure is not necessarily unique; see [ Reference Bochi and Morris9 , Reference Feng and Käenmäki15 , Reference Käenmäki and Morris22 , Reference Käenmäki and Vilppolainen23 ].
Lemma 2·9. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
, contains a rank one matrix, and is dominated or irreducible, then
$\max_{i \in J} \|A_i\| \lt 1$
, contains a rank one matrix, and is dominated or irreducible, then
for all
![]() $0 \leqslant s \leqslant 1$
.
$0 \leqslant s \leqslant 1$
.
Proof. Since
![]() ${\mathsf{A}}$
is dominated or irreducible, Lemma 2·5 shows that
${\mathsf{A}}$
is dominated or irreducible, Lemma 2·5 shows that
![]() $P({\mathsf{A}},s) \gt -\infty$
for all
$P({\mathsf{A}},s) \gt -\infty$
for all
![]() $0 \leqslant s \leqslant 1$
. Notice that, by Lemma 2·2,
$0 \leqslant s \leqslant 1$
. Notice that, by Lemma 2·2,
![]() $P(I^{\mathbb{N}},{\mathsf{A}},0) = \log\# I \lt \log\# J = P({\mathsf{A}},0)$
and we may fix
$P(I^{\mathbb{N}},{\mathsf{A}},0) = \log\# I \lt \log\# J = P({\mathsf{A}},0)$
and we may fix
![]() $0 \lt s \leqslant 1$
. Therefore, by Lemma 2·8, there exists unique
$0 \lt s \leqslant 1$
. Therefore, by Lemma 2·8, there exists unique
![]() $\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
such that
$\mu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
such that
Furthermore, by Lemma 2·7,
![]() $\mu_K$
satisfies
$\mu_K$
satisfies
for all
![]() ${\texttt{i}} \in \Sigma_n$
and
${\texttt{i}} \in \Sigma_n$
and
![]() $n \in {\mathbb{N}}$
, where
$n \in {\mathbb{N}}$
, where
![]() $C \geqslant 1$
is a constant. In particular, if
$C \geqslant 1$
is a constant. In particular, if
![]() $A_k$
is a rank one matrix in
$A_k$
is a rank one matrix in
![]() ${\mathsf{A}}$
, then
${\mathsf{A}}$
, then
![]() $\mu_K([k]) \gt 0$
.
$\mu_K([k]) \gt 0$
.
If
![]() ${\mathsf{A}}$
does not contain invertible matrices, then trivially
${\mathsf{A}}$
does not contain invertible matrices, then trivially
![]() $P(I^{\mathbb{N}},{\mathsf{A}},s) = -\infty$
for all
$P(I^{\mathbb{N}},{\mathsf{A}},s) = -\infty$
for all
![]() $s \gt 0$
and there is nothing to prove. We may thus assume that
$s \gt 0$
and there is nothing to prove. We may thus assume that
![]() ${\mathsf{A}}$
contains an invertible matrix. Therefore, by (5), there exists a measure
${\mathsf{A}}$
contains an invertible matrix. Therefore, by (5), there exists a measure
![]() $\nu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
supported on
$\nu_K \in {\mathcal{M}}_\sigma(J^{\mathbb{N}})$
supported on
![]() $I^{\mathbb{N}}$
such that
$I^{\mathbb{N}}$
such that
Since
![]() $A_k$
is not invertible and
$A_k$
is not invertible and
![]() $\nu_K$
is supported on
$\nu_K$
is supported on
![]() $I^{\mathbb{N}}$
, we have
$I^{\mathbb{N}}$
, we have
![]() $\nu_K([k]) = 0$
. As
$\nu_K([k]) = 0$
. As
![]() $\mu_K$
is the unique measure in
$\mu_K$
is the unique measure in
![]() ${\mathcal{M}}_\sigma(J^{\mathbb{N}})$
satisfying (6) and
${\mathcal{M}}_\sigma(J^{\mathbb{N}})$
satisfying (6) and
![]() $\mu_K([k]) \gt \nu_K([k])$
, we see that
$\mu_K([k]) \gt \nu_K([k])$
, we see that
![]() $\nu_K$
does not satisfy (6) and therefore, by (7),
$\nu_K$
does not satisfy (6) and therefore, by (7),
as claimed.
The following lemma characterises the continuity of the function
![]() $s \mapsto P({\mathsf{A}},s)$
at 1.
$s \mapsto P({\mathsf{A}},s)$
at 1.
Lemma 2·10. If
![]() ${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
${\mathsf{A}} = (A_i)_{i \in J} \in M_2({\mathbb{R}})^J$
satisfies
![]() $\max_{i \in J} \|A_i\| \lt 1$
and is dominated or irreducible, then the function
$\max_{i \in J} \|A_i\| \lt 1$
and is dominated or irreducible, then the function
![]() $s \mapsto P({\mathsf{A}},s)$
is continuous at 1 if and only if
$s \mapsto P({\mathsf{A}},s)$
is continuous at 1 if and only if
![]() ${\mathsf{A}}$
does not contain rank one matrices.
${\mathsf{A}}$
does not contain rank one matrices.
Proof. If
![]() ${\mathsf{A}}$
does not contain rank one matrices, then it contains only invertible or rank zero matrices. By Lemma 2·2, rank zero matrices do not have any effect on the value of the pressure
${\mathsf{A}}$
does not contain rank one matrices, then it contains only invertible or rank zero matrices. By Lemma 2·2, rank zero matrices do not have any effect on the value of the pressure
![]() $P({\mathsf{A}},s)$
when
$P({\mathsf{A}},s)$
when
![]() $s \gt 0$
. Therefore, rank zero matrices have no impact on the continuity at 1 and we may assume that
$s \gt 0$
. Therefore, rank zero matrices have no impact on the continuity at 1 and we may assume that
![]() ${\mathsf{A}} \in GL_2({\mathbb{R}})^J$
. But in this case, the continuity follows from [
Reference Käenmäki and Vilppolainen23
, lemma 2·1].
${\mathsf{A}} \in GL_2({\mathbb{R}})^J$
. But in this case, the continuity follows from [
Reference Käenmäki and Vilppolainen23
, lemma 2·1].
Let us then assume that
![]() ${\mathsf{A}}$
contains a rank one matrix. If
${\mathsf{A}}$
contains a rank one matrix. If
![]() ${\mathsf{A}}$
does not contain invertible matrices, then, as the function
${\mathsf{A}}$
does not contain invertible matrices, then, as the function
![]() $s \mapsto P({\mathsf{A}},s)$
is strictly decreasing, Lemma 2·6 implies that
$s \mapsto P({\mathsf{A}},s)$
is strictly decreasing, Lemma 2·6 implies that
![]() $P({\mathsf{A}},s) = -\infty$
for all
$P({\mathsf{A}},s) = -\infty$
for all
![]() $s \gt 1$
. Furthermore, since
$s \gt 1$
. Furthermore, since
![]() ${\mathsf{A}}$
is dominated or irreducible, Lemma 2·5 shows that
${\mathsf{A}}$
is dominated or irreducible, Lemma 2·5 shows that
![]() $P({\mathsf{A}},s) \gt -\infty$
for all
$P({\mathsf{A}},s) \gt -\infty$
for all
![]() $0 \leqslant s \leqslant 1$
and the function
$0 \leqslant s \leqslant 1$
and the function
![]() $s \mapsto P({\mathsf{A}},s)$
is discontinuous at 1. We may thus assume that
$s \mapsto P({\mathsf{A}},s)$
is discontinuous at 1. We may thus assume that
![]() ${\mathsf{A}}$
contains an invertible matrix. By Lemma 2·6, we thus have
${\mathsf{A}}$
contains an invertible matrix. By Lemma 2·6, we thus have
![]() $P(I^{\mathbb{N}},{\mathsf{A}},s) \gt -\infty$
for all
$P(I^{\mathbb{N}},{\mathsf{A}},s) \gt -\infty$
for all
![]() $s \geqslant 0$
. Recall that, by [
Reference Käenmäki and Vilppolainen23
, lemma 2·1], the function
$s \geqslant 0$
. Recall that, by [
Reference Käenmäki and Vilppolainen23
, lemma 2·1], the function
![]() $s \mapsto P(I^{\mathbb{N}},{\mathsf{A}},s)$
is continuous at 1. Therefore, by Lemma 2·2, showing
$s \mapsto P(I^{\mathbb{N}},{\mathsf{A}},s)$
is continuous at 1. Therefore, by Lemma 2·2, showing
proves the function
![]() $s \mapsto P({\mathsf{A}},s)$
discontinuous at 1. But, as
$s \mapsto P({\mathsf{A}},s)$
discontinuous at 1. But, as
![]() ${\mathsf{A}}$
contains a rank one matrix, this follows immediately from Lemma 2·9.
${\mathsf{A}}$
contains a rank one matrix, this follows immediately from Lemma 2·9.
3. Dimension of non-invertible self-affine sets
Recall that J is a finite set and the affine iterated function system is a tuple
![]() $(f_i)_{i \in J}$
of contractive affine self-maps on
$(f_i)_{i \in J}$
of contractive affine self-maps on
![]() ${\mathbb{R}}^2$
not having a common fixed point. We write
${\mathbb{R}}^2$
not having a common fixed point. We write
![]() $f_i = A_i+v_i$
for all
$f_i = A_i+v_i$
for all
![]() $i \in J$
, where
$i \in J$
, where
![]() $A_i \in M_2({\mathbb{R}})$
and
$A_i \in M_2({\mathbb{R}})$
and
![]() $v_i \in {\mathbb{R}}^2$
, and
$v_i \in {\mathbb{R}}^2$
, and
![]() $f_{\texttt{i}} = f_{i_1} \circ \cdots \circ f_{i_n}$
for all
$f_{\texttt{i}} = f_{i_1} \circ \cdots \circ f_{i_n}$
for all
![]() ${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
![]() $n \in {\mathbb{N}}$
. We let
$n \in {\mathbb{N}}$
. We let
![]() $f_\varnothing = \textrm{Id}$
to be the identity map. Note that the associated tuple of matrices
$f_\varnothing = \textrm{Id}$
to be the identity map. Note that the associated tuple of matrices
![]() $(A_i)_{i \in J}$
is an element of
$(A_i)_{i \in J}$
is an element of
![]() $M_2({\mathbb{R}})^J$
and satisfies
$M_2({\mathbb{R}})^J$
and satisfies
![]() $\max_{i \in J}\|A_i\|\lt 1$
.
$\max_{i \in J}\|A_i\|\lt 1$
.
If
![]() $I = \{i \in J \,:\, A_i \text{ is invertible}\}$
is non-empty, then the invertible self-affine set X is associated to
$I = \{i \in J \,:\, A_i \text{ is invertible}\}$
is non-empty, then the invertible self-affine set X is associated to
![]() $(f_i)_{i \in I}$
, and if
$(f_i)_{i \in I}$
, and if
![]() $J \setminus I$
is non-empty, then the non-invertible self-affine set X
′ is associated to
$J \setminus I$
is non-empty, then the non-invertible self-affine set X
′ is associated to
![]() $(f_i)_{i \in J}$
. Recall the defining property (1) of a self-affine set. We use the convention that whenever we speak about a self-affine set, then it is automatically accompanied with a tuple of affine maps which defines it. This makes it possible to write that e.g. “a non-invertible self-affine set is dominated” which obviously then means that “the associated tuple
$(f_i)_{i \in J}$
. Recall the defining property (1) of a self-affine set. We use the convention that whenever we speak about a self-affine set, then it is automatically accompanied with a tuple of affine maps which defines it. This makes it possible to write that e.g. “a non-invertible self-affine set is dominated” which obviously then means that “the associated tuple
![]() ${\mathsf{A}} = (A_i)_{i \in J}$
of matrices in
${\mathsf{A}} = (A_i)_{i \in J}$
of matrices in
![]() $M_2({\mathbb{R}})^J$
is dominated”.
$M_2({\mathbb{R}})^J$
is dominated”.
The study of non-invertible self-affine sets is connected to the theory of sub-self-affine sets. If the canonical projection
![]() $\pi \colon J^{\mathbb{N}} \to {\mathbb{R}}^2$
is defined such that
$\pi \colon J^{\mathbb{N}} \to {\mathbb{R}}^2$
is defined such that
for all
![]() ${\texttt{i}} = i_1i_2\cdots \in J^{\mathbb{N}}$
, then we write
${\texttt{i}} = i_1i_2\cdots \in J^{\mathbb{N}}$
, then we write
![]() $X^{\prime\prime} = \pi(\Sigma)$
, where
$X^{\prime\prime} = \pi(\Sigma)$
, where
![]() $\Sigma = \{{\texttt{i}} \in J^{\mathbb{N}} \,:\, A_{{\texttt{i}}|_n}$
is non-zero for all
$\Sigma = \{{\texttt{i}} \in J^{\mathbb{N}} \,:\, A_{{\texttt{i}}|_n}$
is non-zero for all
![]() $n \in {\mathbb{N}}\}$
. Observe that
$n \in {\mathbb{N}}\}$
. Observe that
![]() $X = \pi(I^{\mathbb{N}}) \subset X^{\prime\prime} \subset \pi(J^{\mathbb{N}}) = X^{\prime}$
and, as
$X = \pi(I^{\mathbb{N}}) \subset X^{\prime\prime} \subset \pi(J^{\mathbb{N}}) = X^{\prime}$
and, as
![]() $\sigma(\Sigma) \subset \Sigma$
, the set X” is sub-self-affine, i.e.
$\sigma(\Sigma) \subset \Sigma$
, the set X” is sub-self-affine, i.e.
see [
Reference Käenmäki and Vilppolainen23
]. The study is also connected to inhomogeneous self-affine sets. If
![]() $C \subset {\mathbb{R}}^2$
is compact, then there exists a unique non-empty compact set
$C \subset {\mathbb{R}}^2$
is compact, then there exists a unique non-empty compact set
![]() $X_C \subset {\mathbb{R}}^2$
such that
$X_C \subset {\mathbb{R}}^2$
such that
The set
![]() $X_C$
is called the inhomogeneous self-affine set with condensation C. Such sets were introduced by Barnsley and Demko [
Reference Barnsley and Demko7
] and they have been studied for example in [
Reference Baker, Fraser and Máthé1
,
Reference Barnsley6
,
Reference Burrell11
,
Reference Burrell and Fraser12
,
Reference Käenmäki and Lehrbäck21
]. Note that
$X_C$
is called the inhomogeneous self-affine set with condensation C. Such sets were introduced by Barnsley and Demko [
Reference Barnsley and Demko7
] and they have been studied for example in [
Reference Baker, Fraser and Máthé1
,
Reference Barnsley6
,
Reference Burrell11
,
Reference Burrell and Fraser12
,
Reference Käenmäki and Lehrbäck21
]. Note that
![]() $X_\emptyset$
is the invertible self-affine set X.
$X_\emptyset$
is the invertible self-affine set X.
Lemma 3·1. If X′ and X are non-invertible and invertible planar self-affine sets, respectively, and X” is the associated sub-self-affine set defined in (8), then
![]() $X^{\prime} \setminus X^{\prime\prime}$
is countable and
$X^{\prime} \setminus X^{\prime\prime}$
is countable and
where
![]() $X_C$
is the inhomogeneous self-affine set with condensation
$X_C$
is the inhomogeneous self-affine set with condensation
![]() $C = \bigcup_{i \in J \setminus I} f_i(X^{\prime})$
.
$C = \bigcup_{i \in J \setminus I} f_i(X^{\prime})$
.
Proof. Let us first show that
![]() $X^{\prime} \setminus X^{\prime\prime}$
is countable. Writing
$X^{\prime} \setminus X^{\prime\prime}$
is countable. Writing
![]() $v_{\texttt{i}} = \sum_{k=1}^n A_{{\texttt{i}}|_{k-1}}v_{i_k}$
, we see that
$v_{\texttt{i}} = \sum_{k=1}^n A_{{\texttt{i}}|_{k-1}}v_{i_k}$
, we see that
![]() $f_{\texttt{i}} = A_{\texttt{i}} + v_{\texttt{i}}$
for all
$f_{\texttt{i}} = A_{\texttt{i}} + v_{\texttt{i}}$
for all
![]() ${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
${\texttt{i}} = i_1 \cdots i_n \in J^n$
and
![]() $n \in {\mathbb{N}}$
. Let
$n \in {\mathbb{N}}$
. Let
![]() ${\texttt{i}} \in J^{\mathbb{N}} \setminus \Sigma$
and choose
${\texttt{i}} \in J^{\mathbb{N}} \setminus \Sigma$
and choose
![]() $n_0({\texttt{i}}) = \min\{n \in {\mathbb{N}} \,:\, A_{{\texttt{i}}|_n}$
is zero
$n_0({\texttt{i}}) = \min\{n \in {\mathbb{N}} \,:\, A_{{\texttt{i}}|_n}$
is zero
![]() $\}$
. Since
$\}$
. Since
![]() $v_{{\texttt{i}}|_{n+1}} = \sum_{k=1}^{n+1} A_{{\texttt{i}}|_{k-1}}v_{i_k} = A_{{\texttt{i}}|_n} v_{i_{n+1}} + \sum_{k=1}^n A_{{\texttt{i}}|_{k-1}}v_{i_k} = v_{{\texttt{i}}|_n}$
for all
$v_{{\texttt{i}}|_{n+1}} = \sum_{k=1}^{n+1} A_{{\texttt{i}}|_{k-1}}v_{i_k} = A_{{\texttt{i}}|_n} v_{i_{n+1}} + \sum_{k=1}^n A_{{\texttt{i}}|_{k-1}}v_{i_k} = v_{{\texttt{i}}|_n}$
for all
![]() $n \geqslant n_0({\texttt{i}})$
, a simple induction shows that
$n \geqslant n_0({\texttt{i}})$
, a simple induction shows that
for all
![]() $n \geqslant n_0({\texttt{i}})$
. As
$n \geqslant n_0({\texttt{i}})$
. As
![]() $J^{\mathbb{N}} \setminus \Sigma$
is clearly separable, there exist countably many infinite words
$J^{\mathbb{N}} \setminus \Sigma$
is clearly separable, there exist countably many infinite words
![]() ${\texttt{i}}_1,{\texttt{i}}_2,\ldots \in J^{\mathbb{N}} \setminus \Sigma$
such that
${\texttt{i}}_1,{\texttt{i}}_2,\ldots \in J^{\mathbb{N}} \setminus \Sigma$
such that
![]() $J^{\mathbb{N}} \setminus \Sigma \subset \bigcup_{k \in {\mathbb{N}}} [{\texttt{i}}_k|_{n_0({\texttt{i}}_k)}]$
. It follows that
$J^{\mathbb{N}} \setminus \Sigma \subset \bigcup_{k \in {\mathbb{N}}} [{\texttt{i}}_k|_{n_0({\texttt{i}}_k)}]$
. It follows that
is countable.
Let us then prove the claimed equalities. Noting that the argument of [ Reference Snigireva26 , lemma 3·9] works also in the self-affine setting, we have
To prove the remaining equality, let us first show that
![]() $X^{\prime} \subset X_C$
. To that end, fix
$X^{\prime} \subset X_C$
. To that end, fix
![]() $x \in X^{\prime}$
. By (9), we have
$x \in X^{\prime}$
. By (9), we have
![]() $X \subset X_C$
and we may assume that
$X \subset X_C$
and we may assume that
![]() $x \in X^{\prime} \setminus X$
. But this implies that there exist
$x \in X^{\prime} \setminus X$
. But this implies that there exist
![]() ${\texttt{i}} \in I^*$
and
${\texttt{i}} \in I^*$
and
![]() $i \in J \setminus I$
such that
$i \in J \setminus I$
such that
![]() $x \in f_{{\texttt{i}} i}(X^{\prime})$
. Since, again by (9),
$x \in f_{{\texttt{i}} i}(X^{\prime})$
. Since, again by (9),
we have shown that
![]() $X^{\prime} \subset X_C$
. The inclusion
$X^{\prime} \subset X_C$
. The inclusion
![]() $X_C \subset X^{\prime}$
follows immediately from (9) since we trivially have
$X_C \subset X^{\prime}$
follows immediately from (9) since we trivially have
![]() $X \subset X^{\prime}$
and
$X \subset X^{\prime}$
and
![]() $f_{\texttt{i}}(C) \subset X^{\prime}$
for all
$f_{\texttt{i}}(C) \subset X^{\prime}$
for all
![]() ${\texttt{i}} \in I^*$
. Thus
${\texttt{i}} \in I^*$
. Thus
![]() $X^{\prime} = X_C$
as claimed.
$X^{\prime} = X_C$
as claimed.
We are interested in the dimension of the non-invertible self-affine set. Relying on (1), the non-invertible self-affine set X
′ can naturally be covered by the sets
![]() $f_{\texttt{i}}(B)$
, where B is a ball containing X
′. Note that such sets are ellipses or line segments, depending on whether the associated matrix is invertible or has rank one. Each set
$f_{\texttt{i}}(B)$
, where B is a ball containing X
′. Note that such sets are ellipses or line segments, depending on whether the associated matrix is invertible or has rank one. Each set
![]() $f_{\texttt{i}}(B)$
can be covered by one ball of radius
$f_{\texttt{i}}(B)$
can be covered by one ball of radius
![]() $\alpha_1(A_{\texttt{i}}){\textrm{diam}}(B)$
or by
$\alpha_1(A_{\texttt{i}}){\textrm{diam}}(B)$
or by
![]() $\alpha_1(A_{\texttt{i}})/\alpha_2(A_{\texttt{i}})$
many balls of radius
$\alpha_1(A_{\texttt{i}})/\alpha_2(A_{\texttt{i}})$
many balls of radius
![]() $\alpha_2(A_{\texttt{i}}){\textrm{diam}}(B)$
. This motivates us to study the limiting behaviour of sums
$\alpha_2(A_{\texttt{i}}){\textrm{diam}}(B)$
. This motivates us to study the limiting behaviour of sums
![]() $\sum_{{\texttt{i}} \in J^n} {\varphi}^s(A_{\texttt{i}})$
and hence, the pressure
$\sum_{{\texttt{i}} \in J^n} {\varphi}^s(A_{\texttt{i}})$
and hence, the pressure
![]() $P({\mathsf{A}},s)$
.
$P({\mathsf{A}},s)$
.
Recall that the upper Minkowski dimension
![]() ${\overline{\textrm{dim}}_{\textrm{M}}}$
is an upper bound for the Hausdorff dimension
${\overline{\textrm{dim}}_{\textrm{M}}}$
is an upper bound for the Hausdorff dimension
![]() ${\textrm{dim}_{\textrm{H}}}$
for all compact sets; see [
Reference Mattila25
, section 5·3]. The following lemma, generalising [
Reference Falconer14
, theorem 5·4], shows that the affinity dimension is an upper bound for the upper Minkowski dimension for all non-invertible self-affine sets.
${\textrm{dim}_{\textrm{H}}}$
for all compact sets; see [
Reference Mattila25
, section 5·3]. The following lemma, generalising [
Reference Falconer14
, theorem 5·4], shows that the affinity dimension is an upper bound for the upper Minkowski dimension for all non-invertible self-affine sets.
Lemma 3·2. If X′ is a planar self-affine set, then
Proof. We may assume that
![]() ${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) \lt 2$
as otherwise there is nothing to prove. Let
${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) \lt 2$
as otherwise there is nothing to prove. Let
![]() $k \in \{0,1\}$
be such that
$k \in \{0,1\}$
be such that
![]() $k \leqslant {\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) \lt k+1$
. Fix
$k \leqslant {\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) \lt k+1$
. Fix
![]() ${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) \lt s \lt k+1$
and notice that
${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) \lt s \lt k+1$
and notice that
![]() $P({\mathsf{A}},s) \lt 0$
. By [
Reference Falconer14
, proposition 4·1], we thus have
$P({\mathsf{A}},s) \lt 0$
. By [
Reference Falconer14
, proposition 4·1], we thus have
Let B be a ball containing X ′. By scaling and translating, we may assume that B is the unit ball. Write
for all
![]() $0\lt r\lt 1$
. If
$0\lt r\lt 1$
. If
![]() ${\texttt{j}} \in J^{\mathbb{N}}$
, then
${\texttt{j}} \in J^{\mathbb{N}}$
, then
![]() $\alpha_{k+1}(A_{{\texttt{j}}|_0}) = \alpha_{k+1}(\textrm{Id}) = 1$
and
$\alpha_{k+1}(A_{{\texttt{j}}|_0}) = \alpha_{k+1}(\textrm{Id}) = 1$
and
![]() $\alpha_{k+1}(A_{{\texttt{j}}|_n}) \to 0$
as
$\alpha_{k+1}(A_{{\texttt{j}}|_n}) \to 0$
as
![]() $n \to \infty$
. Therefore, for each
$n \to \infty$
. Therefore, for each
![]() $0\lt r\lt 1$
there exists unique
$0\lt r\lt 1$
there exists unique
![]() $n \in {\mathbb{N}}$
such that
$n \in {\mathbb{N}}$
such that
![]() ${\texttt{j}}|_n \in {\mathcal{C}}_r$
and the collection
${\texttt{j}}|_n \in {\mathcal{C}}_r$
and the collection
![]() $\{[{\texttt{i}}] \,:\, {\texttt{i}} \in {\mathcal{C}}_r\}$
of pairwise disjoint cylinder sets is a cover of
$\{[{\texttt{i}}] \,:\, {\texttt{i}} \in {\mathcal{C}}_r\}$
of pairwise disjoint cylinder sets is a cover of
![]() $J^{\mathbb{N}}$
.
$J^{\mathbb{N}}$
.
Fix
![]() $0\lt r\lt 1$
and
$0\lt r\lt 1$
and
![]() ${\texttt{i}} \in {\mathcal{C}}_r$
, and observe that
${\texttt{i}} \in {\mathcal{C}}_r$
, and observe that
![]() $f_{\texttt{i}}(B)$
is an ellipse with semi-axes
$f_{\texttt{i}}(B)$
is an ellipse with semi-axes
![]() $\alpha_1(A_{\texttt{i}})$
and
$\alpha_1(A_{\texttt{i}})$
and
![]() $\alpha_2(A_{\texttt{i}})$
. Since
$\alpha_2(A_{\texttt{i}})$
. Since
![]() $\alpha_{k+1}(A_{\texttt{i}}) \leqslant r \lt \alpha_{k+1}(A_{{\texttt{i}}^-})$
, the set
$\alpha_{k+1}(A_{\texttt{i}}) \leqslant r \lt \alpha_{k+1}(A_{{\texttt{i}}^-})$
, the set
![]() $f_{\texttt{i}}(B)$
is covered by
$f_{\texttt{i}}(B)$
is covered by
 \begin{equation*} \begin{cases} 4, &\text{if } k=0, \\[4pt] 4\max\{r^{-1}\alpha_1(A_{\texttt{i}}),1\}, &\text{if } k=1 \end{cases} \end{equation*}
\begin{equation*} \begin{cases} 4, &\text{if } k=0, \\[4pt] 4\max\{r^{-1}\alpha_1(A_{\texttt{i}}),1\}, &\text{if } k=1 \end{cases} \end{equation*}
many balls of radius r. Notice that
![]() $\max\{r^{-1}\alpha_1(A_{\texttt{i}}),1\} \leqslant r^{-1}\alpha_1(A_{{\texttt{i}}^-})$
and hence,
$\max\{r^{-1}\alpha_1(A_{\texttt{i}}),1\} \leqslant r^{-1}\alpha_1(A_{{\texttt{i}}^-})$
and hence,
![]() $f_{\texttt{i}}(B)$
can be covered by
$f_{\texttt{i}}(B)$
can be covered by
![]() $4{\varphi}^k(A_{{\texttt{i}}^-})r^{-k}$
many balls of radius r. Write
$4{\varphi}^k(A_{{\texttt{i}}^-})r^{-k}$
many balls of radius r. Write
and observe that
for all
![]() ${\texttt{i}} \in {\mathcal{C}}_r$
. Recalling (10), we thus have
${\texttt{i}} \in {\mathcal{C}}_r$
. Recalling (10), we thus have
 \begin{equation} \begin{split} \sum_{{\texttt{i}} \in {\mathcal{C}}_r} N_{\texttt{i}}(r) & \leqslant 4r^{-s}\sum_{{\texttt{i}} \in {\mathcal{C}}_r} {\varphi}^s(A_{{\texttt{i}}^-}) = 4r^{-s}\sum_{{\texttt{j}} \in J^*} \sum_{{\texttt{i}} \in {\mathcal{C}}_r \,:\, {\texttt{i}}^- = {\texttt{j}}} {\varphi}^s({\mathsf{A}}_{{\texttt{j}}}) \\[4pt] & \leqslant 4r^{-s}\sum_{{\texttt{j}} \in J^*} \# J {\varphi}^s(A_{\texttt{j}}) \leqslant 4M\# Jr^{-s}. \end{split} \end{equation}
\begin{equation} \begin{split} \sum_{{\texttt{i}} \in {\mathcal{C}}_r} N_{\texttt{i}}(r) & \leqslant 4r^{-s}\sum_{{\texttt{i}} \in {\mathcal{C}}_r} {\varphi}^s(A_{{\texttt{i}}^-}) = 4r^{-s}\sum_{{\texttt{j}} \in J^*} \sum_{{\texttt{i}} \in {\mathcal{C}}_r \,:\, {\texttt{i}}^- = {\texttt{j}}} {\varphi}^s({\mathsf{A}}_{{\texttt{j}}}) \\[4pt] & \leqslant 4r^{-s}\sum_{{\texttt{j}} \in J^*} \# J {\varphi}^s(A_{\texttt{j}}) \leqslant 4M\# Jr^{-s}. \end{split} \end{equation}
Since
![]() $\{[{\texttt{i}}] \,:\, {\texttt{i}} \in {\mathcal{C}}_r\}$
is a covering of
$\{[{\texttt{i}}] \,:\, {\texttt{i}} \in {\mathcal{C}}_r\}$
is a covering of
![]() $J^{\mathbb{N}}$
, it follows that
$J^{\mathbb{N}}$
, it follows that
![]() $\{f_{\texttt{i}}(B) \,:\, {\texttt{i}} \in {\mathcal{C}}_r\}$
is a covering of X
′. Hence X
′ can be covered by
$\{f_{\texttt{i}}(B) \,:\, {\texttt{i}} \in {\mathcal{C}}_r\}$
is a covering of X
′. Hence X
′ can be covered by
![]() $\sum_{{\texttt{i}} \in {\mathcal{C}}_r} N_{\texttt{i}}(r)$
many balls of radius r. This together with (11) gives
$\sum_{{\texttt{i}} \in {\mathcal{C}}_r} N_{\texttt{i}}(r)$
many balls of radius r. This together with (11) gives
![]() ${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) \leqslant s$
. The proof is finished by letting
${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) \leqslant s$
. The proof is finished by letting
![]() $s \downarrow {\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})$
.
$s \downarrow {\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})$
.
It is easy to construct examples of self-affine sets having dimension strictly less than the affinity dimension. For example, several self-affine carpets have this property. Nevertheless, the classical result of Falconer [ Reference Falconer14 , theorem 5·3] shows that, perhaps rather surprisingly, the Hausdorff dimension of a non-invertible self-affine set equals the affinity dimension for Lebesgue-almost every choice of translation vectors.
Theorem 3·3. If
![]() $X_{\mathsf{v}}^{\prime}$
is a planar self-affine set and
$X_{\mathsf{v}}^{\prime}$
is a planar self-affine set and
![]() ${\mathsf{A}}$
satisfies
${\mathsf{A}}$
satisfies
![]() $\max_{i \in J}\|A_i\|\lt 1/2$
, then
$\max_{i \in J}\|A_i\|\lt 1/2$
, then
for
![]() ${\mathcal{L}}^{2 \#J}$
-almost all translation vectors
${\mathcal{L}}^{2 \#J}$
-almost all translation vectors
![]() $\mathsf{v} = (v_i)_{i \in J} \in ({\mathbb{R}}^2)^{\#J}$
.
$\mathsf{v} = (v_i)_{i \in J} \in ({\mathbb{R}}^2)^{\#J}$
.
Originally, Falconer assumed that the matrices are invertible and their norms are bounded above by
![]() $1/3$
. Solomyak [
Reference Solomyak27
] relaxed the bound to
$1/3$
. Solomyak [
Reference Solomyak27
] relaxed the bound to
![]() $1/2$
which, by the example of Edgar [
Reference Edgar13
], is known to be the best possible. To see that
$1/2$
which, by the example of Edgar [
Reference Edgar13
], is known to be the best possible. To see that
![]() $\min\{2,{\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})\}$
in Theorem 3·3 is a lower bound for the Hausdorff dimension also when the matrices are non-invertible, by Lemma 2·2 it suffices to notice that [
Reference Falconer14
, lemma 2·2] remains valid for all parameters s strictly less than the rank of the matrix.
$\min\{2,{\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})\}$
in Theorem 3·3 is a lower bound for the Hausdorff dimension also when the matrices are non-invertible, by Lemma 2·2 it suffices to notice that [
Reference Falconer14
, lemma 2·2] remains valid for all parameters s strictly less than the rank of the matrix.
Recently a deterministic class of invertible self-affine sets were found for which the Hausdorff dimension equals the affinity dimension. We say that X satisfies the open set condition if there exists a non-empty open set
![]() $U \subset {\mathbb{R}}^2$
such that
$U \subset {\mathbb{R}}^2$
such that
![]() $f_i(U) \cap f_j(U) = \emptyset$
and
$f_i(U) \cap f_j(U) = \emptyset$
and
![]() $f_i(U) \subset U$
for all
$f_i(U) \subset U$
for all
![]() $i,j \in I$
with
$i,j \in I$
with
![]() $i \ne j$
. If such a set U also intersects X, then we say that X satisfies the strong open set condition. The following breakthrough result for self-affine sets is proven by Bárány, Hochman and Rapaport [
Reference Bárány, Hochman and Rapaport2
, theorems 1·1 and 7·1]:
$i \ne j$
. If such a set U also intersects X, then we say that X satisfies the strong open set condition. The following breakthrough result for self-affine sets is proven by Bárány, Hochman and Rapaport [
Reference Bárány, Hochman and Rapaport2
, theorems 1·1 and 7·1]:
Theorem 3·4. If X is an invertible strictly affine strongly irreducible planar self-affine set satisfying the strong open set condition, then
 \begin{align*} {\textrm{dim}_{\textrm{H}}}(X) &= \min\{2,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\}, \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X)) &= \min\{1,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} \end{align*}
\begin{align*} {\textrm{dim}_{\textrm{H}}}(X) &= \min\{2,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\}, \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X)) &= \min\{1,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} \end{align*}
for all
![]() $V \in {\mathbb{RP}^{1}}$
.
$V \in {\mathbb{RP}^{1}}$
.
We emphasise that Theorem 3·4 uses the assumption that the affine iterated function system consists only of invertible maps. It is currently not known whether the result holds also with non-invertible maps. We also remark that Hochman and Rapaport [ Reference Hochman and Rapaport17 ] have recently managed to relax the assumptions of the result. They showed that the strong open set condition can be replaced by exponential separation, a separation condition which allows overlapping.
The following three propositions collect our dimension results for non-invertible self-affine sets.
Proposition 3·5. Suppose that X′ and X are non-invertible and invertible planar self-affine sets, respectively. If
 \begin{align*} {\textrm{dim}_{\textrm{H}}}(X) &= \min\{2,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} \geqslant 1, \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X)) &= \min\{1,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} = 1 \end{align*}
\begin{align*} {\textrm{dim}_{\textrm{H}}}(X) &= \min\{2,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} \geqslant 1, \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X)) &= \min\{1,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} = 1 \end{align*}
for all
![]() $V \in {\mathbb{RP}^{1}}$
, then
$V \in {\mathbb{RP}^{1}}$
, then
![]() ${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}(X)$
and
${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}(X)$
and
![]() ${\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X^{\prime}))=1$
for all
${\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X^{\prime}))=1$
for all
![]() $V \in {\mathbb{RP}^{1}}$
.
$V \in {\mathbb{RP}^{1}}$
.
Proof. To simplify notation, write
![]() $s = {\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})$
. If
$s = {\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})$
. If
![]() $1 \lt s \lt \infty$
, then Lemma 2·2 shows that
$1 \lt s \lt \infty$
, then Lemma 2·2 shows that
![]() ${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) = s \geqslant 1$
. If
${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) = s \geqslant 1$
. If
![]() $s=1$
, then we get
$s=1$
, then we get
![]() $P({\mathsf{A}},t) = P(I^{\mathbb{N}},{\mathsf{A}},t) \lt 0 = P(I^{\mathbb{N}},{\mathsf{A}},1) \leqslant P({\mathsf{A}},1)$
for all
$P({\mathsf{A}},t) = P(I^{\mathbb{N}},{\mathsf{A}},t) \lt 0 = P(I^{\mathbb{N}},{\mathsf{A}},1) \leqslant P({\mathsf{A}},1)$
for all
![]() $1\lt t\lt \infty$
and we again have
$1\lt t\lt \infty$
and we again have
![]() ${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) = s \geqslant 1$
. Therefore, by Lemma 3·2, we have
${\textrm{dim}_{\textrm{aff}}}({\mathsf{A}}) = s \geqslant 1$
. Therefore, by Lemma 3·2, we have
![]() ${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) \leqslant \min\{2,{\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})\} = \min\{2,s\} = {\textrm{dim}_{\textrm{H}}}(X) \leqslant {\textrm{dim}_{\textrm{H}}}(X^{\prime})$
. To finish the proof, notice that
${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) \leqslant \min\{2,{\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})\} = \min\{2,s\} = {\textrm{dim}_{\textrm{H}}}(X) \leqslant {\textrm{dim}_{\textrm{H}}}(X^{\prime})$
. To finish the proof, notice that
![]() $1 = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X)) \leqslant {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X^{\prime})) \leqslant 1$
for all
$1 = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X)) \leqslant {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X^{\prime})) \leqslant 1$
for all
![]() $V \in {\mathbb{RP}^{1}}$
.
$V \in {\mathbb{RP}^{1}}$
.
Proposition 3·6. Suppose that X′ and X are non-invertible and invertible planar self-affine sets, respectively. If X′ is dominated or irreducible,
![]() ${\mathsf{A}}$
contains a rank one matrix,
${\mathsf{A}}$
contains a rank one matrix,
![]() ${\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}}) \lt 1$
, and
${\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}}) \lt 1$
, and
then
![]() ${\textrm{dim}_{\textrm{H}}}(X^{\prime}) \gt {\overline{\textrm{dim}}_{\textrm{M}}}(X)$
.
${\textrm{dim}_{\textrm{H}}}(X^{\prime}) \gt {\overline{\textrm{dim}}_{\textrm{M}}}(X)$
.
Proof. To simplify notation, write
![]() $s={\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})$
. Since
$s={\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})$
. Since
![]() $s \lt 1$
, Lemma 2·9 implies that
$s \lt 1$
, Lemma 2·9 implies that
![]() $0 = P(I^{\mathbb{N}},{\mathsf{A}},s) \lt P({\mathsf{A}},s)$
. Therefore, as Lemmas 2·5 and 2·2 guarantee the continuity of the pressure, we have
$0 = P(I^{\mathbb{N}},{\mathsf{A}},s) \lt P({\mathsf{A}},s)$
. Therefore, as Lemmas 2·5 and 2·2 guarantee the continuity of the pressure, we have
![]() $s \lt {\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})$
. Therefore, by Lemma 3·2, we have
$s \lt {\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})$
. Therefore, by Lemma 3·2, we have
![]() ${\overline{\textrm{dim}}_{\textrm{M}}}(X) \leqslant s \lt \min\{2,{\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})\} = {\textrm{dim}_{\textrm{H}}}(X^{\prime})$
.
${\overline{\textrm{dim}}_{\textrm{M}}}(X) \leqslant s \lt \min\{2,{\textrm{dim}_{\textrm{aff}}}({\mathsf{A}})\} = {\textrm{dim}_{\textrm{H}}}(X^{\prime})$
.
Proposition 3·7. Suppose that X′ and X are non-invertible and invertible planar self-affine sets, respectively. If
![]() ${\mathsf{A}}$
contains a rank one matrix and
${\mathsf{A}}$
contains a rank one matrix and
for all
![]() $V \in {\mathbb{RP}^{1}}$
, then there exists a rank one matrix A in
$V \in {\mathbb{RP}^{1}}$
, then there exists a rank one matrix A in
![]() ${\mathsf{A}}$
such that
${\mathsf{A}}$
such that
![]() ${\textrm{dim}_{\textrm{H}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) \leqslant 1$
.
${\textrm{dim}_{\textrm{H}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) \leqslant 1$
.
Proof. To simplify notation, write
![]() $s = {\textrm{dim}_{\textrm{H}}}(X)$
. By Lemma 3·1, the non-invertible self-affine set can be expressed as an inhomogeneous self-affine set,
$s = {\textrm{dim}_{\textrm{H}}}(X)$
. By Lemma 3·1, the non-invertible self-affine set can be expressed as an inhomogeneous self-affine set,
where
![]() $C = \bigcup_{i \in J \setminus I} f_i(X^{\prime})$
. Therefore, by the countable stability of Hausdorff dimension,
$C = \bigcup_{i \in J \setminus I} f_i(X^{\prime})$
. Therefore, by the countable stability of Hausdorff dimension,
 \begin{equation} \begin{split} {\textrm{dim}_{\textrm{H}}}(X^{\prime}) &= \max\{s, \sup_{{\texttt{i}} \in I^*}{\textrm{dim}_{\textrm{H}}}(f_{\texttt{i}}(C))\} \\[4pt] &= \max\{s, {\textrm{dim}_{\textrm{H}}}(C)\} = \max\{s, \max_{i \in J \setminus I}{\textrm{dim}_{\textrm{H}}}(A_i(X^{\prime}))\}. \end{split} \end{equation}
\begin{equation} \begin{split} {\textrm{dim}_{\textrm{H}}}(X^{\prime}) &= \max\{s, \sup_{{\texttt{i}} \in I^*}{\textrm{dim}_{\textrm{H}}}(f_{\texttt{i}}(C))\} \\[4pt] &= \max\{s, {\textrm{dim}_{\textrm{H}}}(C)\} = \max\{s, \max_{i \in J \setminus I}{\textrm{dim}_{\textrm{H}}}(A_i(X^{\prime}))\}. \end{split} \end{equation}
Let A be a rank one matrix in
![]() ${\mathsf{A}}$
such that
${\mathsf{A}}$
such that
![]() ${\textrm{dim}_{\textrm{H}}}(A(X^{\prime})) = \max_{i \in J \setminus I}{\textrm{dim}_{\textrm{H}}}(A_i(X^{\prime}))$
. Since, by the assumption and Lemma 2·1,
${\textrm{dim}_{\textrm{H}}}(A(X^{\prime})) = \max_{i \in J \setminus I}{\textrm{dim}_{\textrm{H}}}(A_i(X^{\prime}))$
. Since, by the assumption and Lemma 2·1,
![]() $s = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X)) \leqslant {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) = {\textrm{dim}_{\textrm{H}}}(A(X^{\prime}))$
, the claim follows from (12).
$s = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X)) \leqslant {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) = {\textrm{dim}_{\textrm{H}}}(A(X^{\prime}))$
, the claim follows from (12).
We are now ready to prove the main result. The proof basically just applies Theorems 3·3 and 3·4 in the above propositions.
Proof of Theorem 1·1. (i) Since, by Theorem 3·4, we have
 \begin{align*} {\textrm{dim}_{\textrm{H}}}(X) &= \min\{2,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} \geqslant 1, \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X)) &= \min\{1,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} = 1 \end{align*}
\begin{align*} {\textrm{dim}_{\textrm{H}}}(X) &= \min\{2,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} \geqslant 1, \\[4pt] {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{V}(X)) &= \min\{1,{\textrm{dim}_{\textrm{aff}}}(I^{\mathbb{N}},{\mathsf{A}})\} = 1 \end{align*}
for all
![]() $V \in {\mathbb{RP}^{1}}$
, Proposition 3·5 implies
$V \in {\mathbb{RP}^{1}}$
, Proposition 3·5 implies
![]() ${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}(X)$
and
${\overline{\textrm{dim}}_{\textrm{M}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}(X)$
and
![]() ${\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X^{\prime}))=1$
for all
${\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_V(X^{\prime}))=1$
for all
![]() $V \in {\mathbb{RP}^{1}}$
.
$V \in {\mathbb{RP}^{1}}$
.
(ii) Since, by Theorem 3·3, we have
for
![]() ${\mathcal{L}}^{2 \#J}$
-almost all
${\mathcal{L}}^{2 \#J}$
-almost all
![]() $\mathsf{v} \in ({\mathbb{R}}^2)^{\#J}$
, Proposition 3·6 implies
$\mathsf{v} \in ({\mathbb{R}}^2)^{\#J}$
, Proposition 3·6 implies
![]() ${\textrm{dim}_{\textrm{H}}}(X^{\prime}_{\mathsf{v}}) \gt {\overline{\textrm{dim}}_{\textrm{M}}}(X_{\mathsf{v}})$
for
${\textrm{dim}_{\textrm{H}}}(X^{\prime}_{\mathsf{v}}) \gt {\overline{\textrm{dim}}_{\textrm{M}}}(X_{\mathsf{v}})$
for
![]() ${\mathcal{L}}^{2 \#J}$
-almost all
${\mathcal{L}}^{2 \#J}$
-almost all
![]() $\mathsf{v} \in ({\mathbb{R}}^2)^{\#J}$
.
$\mathsf{v} \in ({\mathbb{R}}^2)^{\#J}$
.
(iii) Since, by Theorem 3·4, we have
for all
![]() $V \in {\mathbb{RP}^{1}}$
, Proposition 3·7 implies that there exists a rank one matrix A in
$V \in {\mathbb{RP}^{1}}$
, Proposition 3·7 implies that there exists a rank one matrix A in
![]() ${\mathsf{A}}$
such that
${\mathsf{A}}$
such that
![]() ${\textrm{dim}_{\textrm{H}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) \leqslant 1$
.
${\textrm{dim}_{\textrm{H}}}(X^{\prime}) = {\textrm{dim}_{\textrm{H}}}({\textrm{proj}}_{\ker(A)^\bot}(X^{\prime})) \leqslant 1$
.
Acknowledgements
The authors thank De-Jun Feng for pointing out Lemma 3·2.



