Flexible production technology, between crystal sugar and ethanol, is common in the current Brazilian sugar cane processing industry (Goldemberg, Coelho, and Guardabassi Reference Goldemberg, Coelho and Guardabassi2008, Bastian-Pinto, Brandão and Hahn Reference Bastian-Pinto, Brandão and Hahn2009, Drabik et al. Reference Drabik, de Gorter, Just and Timilsina2015). Although flexible ethanol-sugar plants do not yet operate in the United States, there are efforts underway to commercialize a flexible energy beet-ethanol biorefinery that can produce industrial sugar juice or ethanol, and co-products, in a single facility, in both California and North Dakota (McGrath and Townsend Reference McGrath and Townsend2015, Wamisho, Ripplinger and DeLaporte Reference Wamisho, Ripplinger and De Laporte2015).
A flexible plant configuration allows a biorefinery owner to exercise the option to switch between alternative modes of production in response to changing market conditions. The option to switch between different production processes has value and depends on the market price and cost of production, as well as the correlation between ethanol and sugar juice prices. Thus, the option of choosing between ethanol and sugar juice is equivalent to the option to exchange one risky asset for another (Black and Scholes Reference Black and Scholes1973, Merton Reference Merton1973, Margrabe Reference Margrabe1978, Dixit and Pindyck Reference Dixit and Pindyck1994), and for our study the values of ethanol and sugar are assumed to be the two assets to be exchanged. Although this operational flexibility enhances the biorefinery's ability to cope with output price uncertainty and volatility, the profitability and economic viability of the energy beet biorefinery investment decision is uncertain given several economic factors, including the interaction of the price of energy beets, ethanol, and sugar juice, as well as the competitive environment in which ethanol and sugar are produced.
The purpose of this paper is to design a real-options framework to quantify the real-option value of a flexible biorefinery and evaluate optimal decision rules for switching between the ethanol and sugar modes of production in a single facility. The study implements a real-options pricing approach to compute the threshold prices that signal biorefinery owners to switch between sugar juice and ethanol production, based on current and perspective biochemical processing technology and expected prices for the two outputs in the U.S. Northern Plains product and input markets. Uncertainty within the model arises from the prices of ethanol and sugar, modeled jointly as correlated geometric Brownian motion (GBM) stochastic processes. Comparative statics are used to analyze the effect of changes in parameters of underlying stochastic variables, by taking into account both the drift and volatility of ethanol and sugar prices, and their correlation parameter. GBM results are also compared with mean reversion (MR) process results.
One advantage a flexible biorefinery has over dedicated conventional biofuel plants is its ability to reduce the technical and financial risks associated with new technology deployment through diversification of outputs. In addition, empirical results in Brazilian flex-plants showed the flexible production process of ethanol and sugar added option value due to hedging of ethanol and sugar to each other when there was volatility in market prices of ethanol and sugar (Bastian-Pinto, Brandão, and Hahn Reference Bastian-Pinto, Brandão and Hahn2009).
Ethanol production from sugar beet, sugarcane, and sweet sorghum feedstock are all potential advanced biofuel candidates (Shapouri, Salassi, and Fairbanks Reference Shapouri, Salassi and Fairbanks2006, Outlaw et al. Reference Outlaw, Ribera, Richardson, Silva, Bryant and Steven2007, Coyle Reference Coyle2010, Linton et al. Reference Linton, Miller, Little, Petrolia and Coble2011). Although energy beetsFootnote 1 are specific to the United States, sugar beets are used in Europe for ethanol and sugar production. The energy beet processing plant in this study is designed to produce ethanol, but the plant owner has the option to sell sugar juice as an intermediate feedstock if it is more profitable. The proposed biorefinery has the flexibility to produce ethanol, and/or industrial sugar along with beet pulp and stillage powder as co-products. Figure 1 illustrates the representative biorefinery plant structure and process model of energy beet conversion into ethanol and industrial sugar juice.

Figure 1. Energy Beet to Industrial Sugar, Beet Pulp and Ethanol Process Model (Wamisho et al. Reference Wamisho, Ripplinger and De Laporte2015).
The analysis of flexible switching-option projects has been addressed using contingent claims analysis and dynamic programming (Kulatilaka Reference Kulatilaka1988, Reference Kulatilaka1993, Trigeorgis Reference Trigeorgis1990, Triantis and Hodder Reference Triantis and Hodder1990, Kulatilaka and Trigeorgis Reference Kulatilaka and Trigeorgis1994, Kogut and Kulatilaka Reference Kogut and Kulatilaka1994, He and Pindyck Reference He and Pindyck1992). Kulatilaka (Reference Kulatilaka1988) used a stochastic dynamic programming model to value the options of flexibility arising from the ability to switch between modes of production in flexible manufacturing systems (FMS). Sethi (Reference Sethi and Sethi1990) analyzed process flexibility in different configurations of dedicated and flexible equipment when demand for two products is uncertain. An extensive literature review on flexibility in the manufacturing sector can be found in the early work of Sethi and Sethi (Reference Sethi and Sethi1990). In addition, Trigeorgis (Reference Trigeorgis1990) demonstrated how an option-pricing approach may be used to value managerial flexibility in flexible plant operations. Most importantly flexible technology provides the firm with a hedge against demand uncertainty, but at a higher investment cost than nonflexible alternatives (Van Mieghem Reference Van Mieghem1998, Fine and Freund Reference Fine and Freund1990).
The decision to invest in a new flex beet ethanol refinery is a dynamic process, affected largely by volatility in prices of ethanol, sugar, and feedstock; irreversible investments; and the policy environment in which ethanol industry functions. Because beet ethanol refinery investments have large sunk costs and plant operations in an uncertain market environment, potential investors can delay investment decisions until additional price, cost, and policy information is available (Hossiso and Ripplinger Reference Hossiso and Ripplinger2016). Evaluating investment projects using the conventional discounted cash flow techniques such as the net-present value (NPV) and break-even value approach may result in biased outcomes. One of the most important limitations of NPV is that it fails to adequately account for managerial flexibility, and the risk and uncertainty of future cash flows, including ethanol and major input prices as well as sunk cost. The NPV investment decision rule is based on the Marshallian concept of the theory of entry and exit. In essence, the drawbacks of this methodology are that it ignores the opportunity cost of waiting for new information, and that it assumes that future cash flows follow a constant pattern that can be accurately predicted. Overall, the NPV approach is not flexible when an investment is irreversible and the decision to invest can be postponed (Dixit Reference Dixit1989, Pindyck Reference Pindyck1991, Dixit and Pindyck Reference Dixit and Pindyck1994).
Recent literature uses real options techniques to analyze key factors affecting ethanol investment decisions including government subsidy policies, economic factors, and strategic interactions in the ethanol industry sector in the United States and Canada (Schmitt et al. Reference Schmit, Luo and Tauer2009, Reference Schmit, Luo and Conrad2011, Gonzalez, Karali and Wetzstein 2012, Cai and Stiegert 2014, Thome and Lin 2015, Lin and Yi Reference Lin and Yi2015a, Reference Lin and Yi2015b, Yi, Lin and Thome Reference Yi, Lin and Thome2015). However, all of these studies analyzed investment on dedicated configurations mostly in ethanol plants producing ethanol and its co-products. The study most closely related to our analysis, by Bastian-Pinto, Brandão and Hahn (Reference Bastian-Pinto, Brandão and Hahn2009), analyzed the production switching option available to a Brazilian flexible sugar–ethanol plant. Additionally, Tareen, Wetzstein, and Duffield (Reference Tareen, Wetzstein and Duffield2000), and Vedenov, Duffield, and Wetzstein (Reference Vedenov, Duffield and Wetzstein2006) used a real-options approach to determine the threshold prices at which transportation fuel purchasers should shift from petroleum diesel to biodiesel, or from conventional gasoline to ethanol blends, respectively. Methodologically, our paper is closely related to the broader real options value approach by Dixit and Pindyck (Reference Dixit and Pindyck1994), and the framework of the empirical model is adapted from Tareen et al. (Reference Tareen, Wetzstein and Duffield2000) and Vedenov et al. (Reference Vedenov, Duffield and Wetzstein2006).
The application of switching options techniques to flexible ethanol plant investment analysis makes several important contributions to the literature and to potential flexible ethanol investors. In addition, our real-options framework demonstrates the role of ethanol and sugar price uncertainty in determining the optimal switching threshold boundary. To best of our knowledge, the real-options framework has not been applied to flexible ethanol plants in the United States. Most analysis so far has been generally limited to investment projects that are dedicated to specific products. Therefore, the results of this analysis provide valuable information for potential investors and policymakers, given that policy interests regarding biofuel industry expansion are shifting toward development of flexible biofuel plants. Finally, the switching option compares two alternative stochastic price evolution processes (GBM and MR) for two competing output choices.
The remainder of the paper is organized as follows. Section 2 reviews policy and market environment of ethanol production and consumption in the United States and Brazil. Section 3 constructs the analytical model to compute switching threshold prices and decision rules for switching options. Section 4 depicts the construction of data and stochastic-process parameters. The last two sections present results and discuss the empirical analysis, and conclusions and policy implications of the study.
Overview of Ethanol Policy and Market Environment in the United States and Brazil
This section provides an overview of the ethanol industry structure and policy environments in the United States and Brazil. In the current biofuel market, the United States and Brazil are the two leading ethanol producing countries. In 2015, global ethanol production topped 25.7 billion gallons (bg), with the United States and Brazil producing 58 and 28 percent of this quantity, respectively (RFA 2016). For the most part, biofuel policies and market factors in both countries have reshaped the global market demand and supply of ethanol and the competitiveness of biofuel industry.
In the United States, the Energy Independence and Security Act of 2007 (EISA 2007) played a key role in solidifying investments in renewable energy and the biobased economy. The main goal of the EISA was reducing foreign oil dependence and greenhouse gas emissions (GHGs), promoting a clean-energy economy and supporting rural economy by providing several subsidies in the form of tax credits and renewable fuel mandates. The U.S. mandates and tax credits policies, along with spikes in crude oil prices, propelled rapid expansion of ethanol production and consumption. For example, from 2001 to 2015, production of ethanol jumped from 1.8 to 13.7 billion gallons per year (bgy), and the United States becoming the largest net exporter of ethanol since 2010 (RFA 2016, Nebraska Energy Office 2016). In 2015 alone, the United States exported some 856 million gallons of ethanol. As of July 2016, installed production capacity at U.S. plants was 15.6 bg, with operating refineries producing 15.1 bgy, with expansion plans for an additional 162.0 million gallons (Nebraska Energy Office 2016). Given the installed capacity, it is feasible for the United States biofuel industry to produce the annual conventional ethanol mandates target set for 2015 and beyond by the Renewable Fuel Standard (RFS2).
The Brazilian National Alcohol Program (PROÁLCOOL) was implemented to reduce imported foreign oil after the 1970s oil shock. PROÁLCOOL provided various subsidies including a 20 percent mandated blend of ethanol in Brazilian motor fuels, and subsidized loans to invest in ethanol facilities. Additionally, Brazil develops pure and flexible ethanol cars, and various infrastructure-facilitating ethanol production and consumption, to keep ethanol prices competitive with gasoline (Goldemberg Reference Goldemberg2006, UNICA 2010). Currently in Brazil, there are about 300 flex plants that can adjust their mix of ethanol and sugar within a production year from 65–35 percent, depending on the predominant economic conditions (UNICA 2010, Drabik et al. Reference Drabik, de Gorter, Just and Timilsina2015).
Ethanol supply-side expansion continued even after the PROÁLCOOL program ended in the 1990s. From 2008 to 2014, sugarcane area increased 35 percent. Sugarcane now accounts for 14 percent of Brazil's total cropland (Valdes, Hjort, and Seeley Reference Goldemberg, Coelho and Guardabassi2016). Most importantly, Brazil still has enormous capacity for future expansion of sugarcane acreage without competing with food-crop acreage (Goldemberg et al. Reference Goldemberg, Coelho and Guardabassi2008, Nassar et al. Reference Nassar, Rudorff, Antoniazzi, de Aguiar, Bacchi and Adami2008, Crago et al. Reference Crago, Khanna, Barton, Guiliani and Amaral2010), Meanwhile in the United States, any expansion of corn as well as dedicated energy-crop acreage for ethanol production must come largely through reduction in the acreage of other crops (Crago et al. Reference Crago, Khanna, Barton, Guiliani and Amaral2010). Thus, Brazil has the potential to expand ethanol exports more rapidly than any other country by diverting more sugarcane into ethanol production (Valdes, Hjort, and Seeley Reference Valdes, Hjort and Seeley2016).
Feedstock cost comprises have the largest share of total ethanol production cost, and it is crucial for ethanol industry to be competitive in the transportation fuel market. Various studies indicate that Brazil has the lowest ethanol production costs relative to other ethanol-producing countries, including the United States, with corn ethanol, making its sugarcane ethanol competitive in the global ethanol market (e.g., Martines-Filho et al. Reference Martines-Filho, Burnquist and Vian2006, Organisation for Economic Co-operation and Development 2006). The reported relative cost advantages vary by study, from 32 percent (Crago et al. Reference Crago, Khanna, Barton, Guiliani and Amaral2010) for the 2006–2008 period to 58 percent lower than for corn ethanol produced in the United States. This cost advantage is largely attributed to cost of land in Brazil being significantly lower than in the United States (Cargo et al. 2010, Valdes Reference Valdes2011). However, when transport cost of sugarcane ethanol from Brazil is factored and co-product credits for corn ethanol are taken into account, the cost of imported sugarcane ethanol at the United States port is 17 percent higher than corn ethanol (Crago et al. Reference Crago, Khanna, Barton, Guiliani and Amaral2010).
Ethanol yield from each feedstock shows that Brazilian sugarcane provides 713 gallons of ethanol per acre compared to 427 gallons for corn ethanol in the United States. (Shapouri, Salassi, and Fairbanks Reference Shapouri, Salassi and Fairbanks2006, Valdes Reference Valdes2011). However, energy beet trial results in North Dakota show that beet ethanol provides 757 gallons of ethanol per acre (Wamisho et al. Reference Wamisho, Ripplinger and De Laporte2015), implying the possibility of obtaining more ethanol from sugar beets per unit of land than corn. In addition, the production of ethanol from sugar is very straightforward because the substrate is a solution of simple sugar molecules rather than a large solid polymer of starch. As such, sugar-based processes require less unit operations than starch- or cellulose-based production processes. These two attributes have implications for reduction of life cycle GHGs relative to gasoline fuel.
A study on the tradeoff between ethanol and sugar production in Brazil that occurs in a sugarcane processing flex-plant showed that a change in Brazilian ethanol policy or a shock in world sugar markets can affect United States ethanol and corn prices (Drabik et al. Reference Drabik, de Gorter, Just and Timilsina2015). Recent analysis shows that there is a positive impact on prices of ethanol and sugar in Brazil as a result of higher gasoline prices, blending fuel mandates, and ethanol tax exemptions (de Gorter et al. Reference de Gorter, Drabik, Kliauga and Timilsina2013). Overall, the market prices of sugarcane and corn ethanol depend largely on a combination of each country's ethanol policies, including blender's tax credits and mandates, the price of gasoline, and the substitutability between gasoline and ethanol (Crago et al. Reference Crago, Khanna, Barton, Guiliani and Amaral2010, Serra et al. Reference Serra, Zilberman and Gil2011, Drabik et al. Reference Drabik, de Gorter, Just and Timilsina2015). For example, higher gasoline prices, blending fuel mandates, and ethanol tax exemptions increase ethanol and sugar prices (de Gorter et al. Reference de Gorter, Drabik, Kliauga and Timilsina2013). Because Brazilian and U.S. ethanol prices have become linked, a change in Brazilian ethanol policy or a shock in world sugar markets can now affect U.S. ethanol and corn prices (Gorter et al. Reference de Gorter, Drabik, Kliauga and Timilsina2013, Drabik et al. Reference Drabik, de Gorter, Just and Timilsina2015).
Empirical Model
Assume that a representative biorefinery owner decides to invest in a flexible beet ethanol plant that produces ethanol and sugar juice, at the beginning of the time horizon [0, T]. Each output results in a different stream of cash flows to the biorefinery owner. In certain kinds of analyses, this means that, based on the information about the project values available at that time, the project with the highest NPV is undertaken. However, because the future prices of ethanol and sugar are uncertain, the present value analysis does not account for managerial flexibility and uncertainty arising from price volatility. The real-options method, in which a refinery owner is assumed to have the flexibility to switch between ethanol and sugar, addresses some of the limitations of NPV-based analysis. The real options payoff for the flexible beet biorefinery plants is specified as:
Where E t denotes the expectation operator conditional on information available at time t under the risk-neutral measure. Expectations E t (π e ) and E t (π s ) are expected profits from producing ethanol and sugar at time t, respectively, considering the mode choice decision at time T 2. T is the terminal year for a planning horizon, and r is the discount rate.
For ease of analytical tractability, we make a few key assumptions. First, the total capital cost and dedicated labor and management remain constant for the flexible plant, irrespective of which outputs are produced. We also assume once the investment decision is made, it cannot be reversed later (i.e., sunk costs cannot be fully recovered) (Dixit and Pindyck Reference Dixit and Pindyck1994). Second, we assume that switching between ethanol and sugar does not require much plant modification and is done without incurring any adjustment costs. Thus, we define flexibility as the capability of switching between the alternative modes of production at no cost. To this end, a switching option can be exercised in each period without cost (after the initial cost of investment is made in a flexible plant). Third, given the way the energy beet ethanol plant is expected to operate in the market, we assume that the price of ethanol and sugar are the two stochastic state variables that affect the option value of switching production at time t. Although energy beet feedstock is a critical variable determining the profit uncertainty of the biorefinery, currently there are no market prices for this feedstock to determine the stochastic nature of this input. Finally, given the lack of historical market price series for sugar juice, raw beet sugar prices are used as a proxy indicator to recover stochastic process parameters for valuation of the option of producing industrial sugar juice.
Based on the above assumptions, the decision to switch to alternative modes of production is made based on the price of ethanol and sugar juice. For analytical convenience, we collapse equation (1) into price space. Hence the expected present value, V, of switching from ethanol to sugar juice at the current prices is derived as:
 $$V = E \mathop\int \limits_0^T {e^{ - rt}[P_e(t) - P_s(t)]dt} $$
$$V = E \mathop\int \limits_0^T {e^{ - rt}[P_e(t) - P_s(t)]dt} $$
Where P e (t) and P s (t) are the price of ethanol and sugar at time t, respectively. This discounted present value is the difference in revenue over the life of the plant, given that all other costs associated with plant operation remain the same across the two alternative products. The analytical model in the section to follow is based on Dixit and Pindyck's (Reference Dixit and Pindyck1994) real-options value approach and the mathematical layout is directly adapted from Tareen et al. (Reference Tareen, Wetzstein and Duffield2000), and Vedenov et al. (2006).
If we assume the stochastic variables evolve according to GBM, the stochastic equations for the ethanol and sugar price variables are defined by the following stochastic equations:
where dP
e
and dP
s
represent the change in the prices of ethanol (P
e
) and sugar(P
s
), respectively, subscript ‘e’ and ‘s’ denote ethanol and sugar, respectively, η
e
and η
s
are drift rates, σ
e
and σ
s
are the standard deviations (volatility) of prices, dz
e
and dz
s
are the increments of the Wiener processes of P
e
and P
s
with
![]() $dz_e = \varepsilon _{te}\sqrt {dt} $
and
$dz_e = \varepsilon _{te}\sqrt {dt} $
and
![]() $dz_s = \varepsilon _{ts}\sqrt {dt} $
, respectively. ε
te
and ε
ts
are drawn from the standard normal distribution N(0,1). The increment of a Wiener process is dz with
$dz_s = \varepsilon _{ts}\sqrt {dt} $
, respectively. ε
te
and ε
ts
are drawn from the standard normal distribution N(0,1). The increment of a Wiener process is dz with
![]() $E\lsqb dz_e^2 \rsqb = E\lsqb dz_s^2 \rsqb = dt$
and E[dz
e
, dz
s
] = ρ
es
dt, where ρ
es
denotes the correlation coefficient between P
e
and P
s
, where
$E\lsqb dz_e^2 \rsqb = E\lsqb dz_s^2 \rsqb = dt$
and E[dz
e
, dz
s
] = ρ
es
dt, where ρ
es
denotes the correlation coefficient between P
e
and P
s
, where
![]() $\rho _{es} = {{\rm cov} \lpar dz_e\comma \; dz_s\rpar } /\/\! \sqrt{{\rm var} \lpar dz_e\rpar \comma \; {\rm var} \lpar dz_s\rpar }$
$\rho _{es} = {{\rm cov} \lpar dz_e\comma \; dz_s\rpar } /\/\! \sqrt{{\rm var} \lpar dz_e\rpar \comma \; {\rm var} \lpar dz_s\rpar }$
Using equations (3) and (4), the expected value of the price of ethanol and sugar at time t can be derived as
where P e (0) and P s (0) are the current prices of ethanol and sugar, respectively. Substituting equation (5) into (2) and performing the integration over time yields the discounted present value of revenue maximizing by switching to the sugar mode of production is given in equation (6).
This option to switch to sugar juice mode of production has no return until the time of switching, so the only return from holding the option to switch is its expected capital appreciation, E[dF]. The Bellman equation for determining the optimal threshold equates to the total expected return on investment as presented in equation (7).
Equation (7) implies that, over a time interval dt, the total expected return on the investment opportunity, rF(V i )dt, is equal to its expected rate of capital appreciation (Dixit and Pindyck, Reference Dixit and Pindyck1994 p. 140). Expanding dF using Ito's lemma and substituting equations (3) and (4) results in a partial differential equation for V, with P e and P s as independent variables, gives us
 $$\eqalign{& \displaystyle{1 \over 2}\lpar {\sigma _e^2 P_{\,p_e}^2 V_{\,p_ep_e} + 2\rho \sigma _e\sigma _sP_{\,p_e}P_{\,p_s}V_{\,p_sp_e} + \sigma _s^2 P_{\,p_s}^2 V_{\,p_sp_s}} \rpar \cr & \quad+ \eta _eP_{\,p_e}V_{\,p_e} + \eta _sP_{\,p_s}V_{\,p_s} - rF = 0} $$
$$\eqalign{& \displaystyle{1 \over 2}\lpar {\sigma _e^2 P_{\,p_e}^2 V_{\,p_ep_e} + 2\rho \sigma _e\sigma _sP_{\,p_e}P_{\,p_s}V_{\,p_sp_e} + \sigma _s^2 P_{\,p_s}^2 V_{\,p_sp_s}} \rpar \cr & \quad+ \eta _eP_{\,p_e}V_{\,p_e} + \eta _sP_{\,p_s}V_{\,p_s} - rF = 0} $$
Equation (8) can be reduced to an ordinary second-order linear differential equation by implementing the homogeneity of the value function in both prices:
Where Φ = P
e
/P
s
and
![]() $\sigma ^2 = \sigma _e^2 - 2 \rho \sigma _e \sigma _s + \sigma _s^2 $
$\sigma ^2 = \sigma _e^2 - 2 \rho \sigma _e \sigma _s + \sigma _s^2 $
The general solution to equation (10) is
Where
![]() $A \prec 0$
, B = 0,
$A \prec 0$
, B = 0,
![]() $\beta \succ 1$
,
$\beta \succ 1$
,
![]() $\alpha \prec 0$
.
$\alpha \prec 0$
.
The value of A and B are constants to be determined, and β and α are the roots of the quadratic equation (Dixit and Pindyck Reference Dixit and Pindyck1994, p. 217). The value-matching condition is
The corresponding smooth-pasting conditions are
Solving equations (12) and (13) yields equation (4), i.e., the optimal switching threshold price:
Where
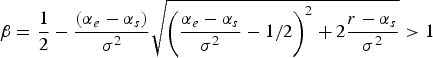 $\beta = \displaystyle{1 \over 2} - \displaystyle{{(\alpha _e - \alpha _s)} \over {\sigma ^2}} \sqrt{{{\left(\displaystyle{{\alpha _e - \alpha _s} \over {\sigma ^2}} - {1 / 2}\right)}^2} + {2\displaystyle{{r - \alpha _s} \over {\sigma ^2}}}} \gt 1$
,
$\beta = \displaystyle{1 \over 2} - \displaystyle{{(\alpha _e - \alpha _s)} \over {\sigma ^2}} \sqrt{{{\left(\displaystyle{{\alpha _e - \alpha _s} \over {\sigma ^2}} - {1 / 2}\right)}^2} + {2\displaystyle{{r - \alpha _s} \over {\sigma ^2}}}} \gt 1$
,
The optimal decision rule for switching to sugar production mode is when its price P
s
is greater than the threshold value
![]() $P_s^ {\ast}$
, otherwise the biorefinery plants owner is more profitable continue producing ethanol.
$P_s^ {\ast}$
, otherwise the biorefinery plants owner is more profitable continue producing ethanol.
Data and Model Parameters
Historical ethanol and sugar price series are used to parameterize the stochastic processes from January, 2000 to December, 2014. Ethanol prices are obtained from the Nebraska Energy Office (2016), representing average rack (wholesale) prices (FOB Omaha, NE). Monthly wholesale refined beet sugar prices for the Midwest market are obtained from the U.S. Department of Agriculture's Economic Research Service (USDA-ERS 2015). The nominal ethanol price series is deflated into real terms using the urban consumer price index (U.S. Department of Labor's Bureau of Labor Statistics 2015), whereas producer price indices for corn sweeteners and sugar are used to deflate the nominal sugar price series (USDA-ERS 2015). Figure 2 shows how ethanol and raw sugar prices have evolved over time.

Figure 2. Historical Monthly Ethanol and Refined Raw Beet Sugar Price
An Augmented Dickey–Fuller (ADF) test is applied to determine if the ethanol and sugar price processes follow a random walk or have a unit root. The null hypothesis is that the dP e and dP s variables contain a unit root, and the alternative is that both variables were generated by a stationary process. GBM requires dP e and dP s in equations (3) and (4) to have a unit root. We conduct two different types of tests: the null hypothesis including a drift term with and without the time trend (see Table 1). The t-test results for the ethanol price series support rejection of the presence of a unit root at all significance levels for the regression with a time trend. Under random walk, without the time trend, we can reject the null hypothesis of a unit root at all significance levels of the log of ethanol price. However, considering a random walk with a time trend, we cannot reject the null hypothesis that ethanol price exhibits a unit root at any significance level. Test results for the sugar price series indicate that we cannot reject the presence of a unit root at all significance levels for the regression, with and without a time trend. However, regression without a time trend shows mixed results. The tests do not reject the presence of unit root at the 99-percent confidence interval. The ADF test results showed only weak arguments against the presence of unit roots in ethanol price series. Failure to reject the random walk hypothesis does not necessarily preclude the existence of autoregression (MR) in the variable of interest (Dixit and Pindyck Reference Dixit and Pindyck1994). The stochastic processes for ethanol and sugar are determined through Itô’s lemma (Dixit and Pindyck Reference Dixit and Pindyck1994). Thus, we use GBM processes in our baseline model, and later compare with MR processes results.
Table 1. Augmented Dickey-Fuller (ADF) test for Unit Root test

Note: CV represents critical value.
If we assume that the market price of ethanol and sugar evolves exogenously over time through GBM as in eqns. (3) and (4), which is the continuous-time formulation of the random walk, then lnP follows a Brownian motion with drift parameter
![]() $\eta = \beta - \displaystyle{1 \over 2}\sigma ^2$
, and volatility, σ. The total derivative of lnP is given as:
$\eta = \beta - \displaystyle{1 \over 2}\sigma ^2$
, and volatility, σ. The total derivative of lnP is given as:
Where P represents the vector of sugar and ethanol prices. We run regression for each price series independently and compute each drift as
![]() $\eta = \hat \beta - 0.5\sigma ^2$
, and volatility (σ), of ethanol and sugar along with their correlation coefficients, ρ. The volatility parameter for both price series are the root mean square errors (RMSE) from the regression estimation results of equation (15).
$\eta = \hat \beta - 0.5\sigma ^2$
, and volatility (σ), of ethanol and sugar along with their correlation coefficients, ρ. The volatility parameter for both price series are the root mean square errors (RMSE) from the regression estimation results of equation (15).
On the other hand, the simplest form of the MR process is the single factor Ornstein-Uhlenbeck process that assumes the random variable will revert to a long-term average, as described by equation (16) below:
Where P is the vector log of ethanol and sugar prices, ϕ is the MR coefficient,
![]() $\bar P$
is the log of the long-term mean price, σ is the volatility of the price process, and dz is the Weiner process.
$\bar P$
is the log of the long-term mean price, σ is the volatility of the price process, and dz is the Weiner process.
From the regression, the mean-reversion coefficient is computed as
![]() $\varphi = \displaystyle{{ - \ln \lpar \beta + 1\rpar } \over {\Delta t}}$
, the volatility is
$\varphi = \displaystyle{{ - \ln \lpar \beta + 1\rpar } \over {\Delta t}}$
, the volatility is
 $\sigma = \sigma _\varepsilon \sqrt {\displaystyle{{2\ln \lpar \beta _1 + 1\rpar } \over {\Delta t\lsqb {\lpar \beta _1 + 1\rpar }^2 - 1\rsqb }}} $
and long-term mean price (
$\sigma = \sigma _\varepsilon \sqrt {\displaystyle{{2\ln \lpar \beta _1 + 1\rpar } \over {\Delta t\lsqb {\lpar \beta _1 + 1\rpar }^2 - 1\rsqb }}} $
and long-term mean price (
![]() $\bar P$
) is computed as
$\bar P$
) is computed as
![]() $\bar P = \exp \left[{ - \displaystyle{{\beta _0} \over {\beta _1}} + \displaystyle{{\sigma ^2} \over {2\eta}}} \right]$
. Where σ
ε is the variance of the regressions’ errors as obtained as a root mean square error (RMSE) from the regression estimation results of equation (15). For both GBM and MR models, the correlation coefficient, ρ, between the prices of ethanol and sugar is calculated as the correlation between the first differences in logged ethanol and sugar prices.
$\bar P = \exp \left[{ - \displaystyle{{\beta _0} \over {\beta _1}} + \displaystyle{{\sigma ^2} \over {2\eta}}} \right]$
. Where σ
ε is the variance of the regressions’ errors as obtained as a root mean square error (RMSE) from the regression estimation results of equation (15). For both GBM and MR models, the correlation coefficient, ρ, between the prices of ethanol and sugar is calculated as the correlation between the first differences in logged ethanol and sugar prices.
To investigate the effect of increasing ethanol price volatility starting late 2006 (see Figure 2), the sample is split into two periods; January 2000–December 2014 is the full sample period, and August 2006–December 2014 is the subsample period. Point estimates of β, volatility and drift parameters for both sample periods under GBM and MR processes are presented in Tables 2 and 3, respectively. For example, point estimates of β in the full and subsample periods for ethanol are −0.043 and −0.153 and are statistically significant at the 95 percent confidence interval. For sugar, the point estimates of β are −0.01 and −0.025, but are not statistically significant at all levels.
Table 2. Regression results for deflated prices of sugar and ethanol

Standard errors in parentheses, + p < 0.10, * p < 0.05, ** p < 0.01, *** p < 0.001.
Table 3. Baseline Stochastic process parameters of GBM and MR in full and subsample period

In fact, historical prices of ethanol and raw sugar are positively correlated as indicated by our estimation results (0.17 and 0.25). In response to this possibility, we later test the sensitivity of our results to the effect of different values of correlation, including negative correlation between the two-price series. Consistent with the observation in Figure 1, the price of ethanol has higher volatility than that of sugar, or a ton of energy beets, regardless of type of stochastic process and data samples assumed.
To compare relative switching threshold prices, we first compute the ethanol equivalent break-even price of industrial sugar juice based on the mass and material balances of a ton of energy beets. A ton of energy beets produces 328 pounds of raw, thick juice, or 26.2 gallons of ethanol. In the process model, Figure 1, the raw, thick juice can be converted into industrial sugar juice or/and to ethanol. The unit cost of juice production is $2.17 per gallon. This unit cost of sugar juice is the same, whether the biorefinery plant prefers the ethanol or industrial sugar juice production mode. Details of the operating and investment costs in our representative flexible energy beet biorefinery are reported in Table 4. The fermentation, distillation, and dehydration process produces ethanol and stillage powder, and the unit cost for this process is estimated at $0.093/gal. Thick sugar can be preserved and stored as thick juice under controlled acidic and alkaline conditions (Vargas-Ramirez et al. Reference Vargas-Ramirez, Haagenson, Pryor and Wiesenborn2013, Reference Vargas-Ramirez, Haagenson, Pryor and Wiesenborn2016) before it is fully converted into industrial sugar juice. Industrial sugars are carbohydrates that can be used to produce value-added products (Vargas-Ramirez et al. Reference Vargas-Ramirez, Haagenson, Pryor and Wiesenborn2016). The costs associated with conditioning chemicals and storage in the conversion process is estimated to be $0.011/gal ethanol equivalent (Vargas-Ramirez et al. Reference Vargas-Ramirez, Haagenson, Pryor and Wiesenborn2013, Reference Vargas-Ramirez, Haagenson, Pryor and Wiesenborn2016). Thus, the break-even price of sugar juice (P s ) is $2.17 per gallon.
Table 4. Deterministic Bases Case Operating Cash Flow

Source: Wamisho, Ripplinger and De Laporte (Reference Wamisho, Ripplinger and De Laporte2015).
Note: Pulp credits = $ 0.398 per gallon. Break-even price of thick juice is the sum of all costs less costs of chemical, enzyme, and denaturant. The cost of chemical that comprises sulfuric acid and alkaline for conditioning raw thick juice and storage is converted from Vargas-Ramirez et al. (2015).
The beet pulp produced as a byproduct is obtained irrespective of which production model the biorefinery employs. Hence, the beet pulp credits, $0.398 per gallon, is not included in the break-even calculation to compare the cost of industrial sugar juice and ethanol production. As such, adding the beet pulp credits in both sides of the output is equivalently cancelled out again. These assumptions greatly simplify the analysis and allow a direct comparison of the stochastic prices of ethanol and sugar juice. We assume that the flexible biorefinery has a useful economic life of ten years with a discount rate of 8.25 percent per annum. For the case of ethanol production, the costs of enzymes, chemicals and denaturants are the differences compared to industrial sugar juice.
Empirical Results and Discussion
This paper presents the empirical results in three distinct sections. The first section discusses the results from the baseline solution, while the second section presents results from the sensitivity analysis using key parameters. The third section provides the relative competiveness of sugar beet versus corn ethanol, and investigates the broader market and policy that surrounds biofuels ethanol.
Because we assume that the switching option decision is made on an annual basis, the real-options switching threshold prices are calculated after converting monthly drift and volatility parameters to annual equivalents, assuming that both the drift rate and variance of the increments of a Brownian motion are linear in time. Due to the lack of statistical significance of the β parameter on sugar price, the baseline threshold switching price is obtained, considering the drift rate of sugar as zero. These switching threshold prices are the price levels above which it becomes economically optimal to switch to sugar juice. Thus, the optimal decision rule is to switch to sugar juice if the optimal threshold price (
![]() $P_s^ {\ast} $
) is greater than $2.17 per gallon. If
$P_s^ {\ast} $
) is greater than $2.17 per gallon. If
![]() $P_s^ {\ast}$
is equal to $2.17 per gallon the biorefinery owner is indifferent to switching between the two modes of production. As described in the methodology section, because there is no historical market price for sugar juice, we rely on the break-even value of sugar juice that is measured in ethanol equivalents as a price reference to make switching decisions.
$P_s^ {\ast}$
is equal to $2.17 per gallon the biorefinery owner is indifferent to switching between the two modes of production. As described in the methodology section, because there is no historical market price for sugar juice, we rely on the break-even value of sugar juice that is measured in ethanol equivalents as a price reference to make switching decisions.
Baseline Results
The baseline results for the full and subsample periods show that the switching threshold prices (
![]() $P_s^{\ast} $
) are $6.54 and $5.07 per gallon, respectively, which are far greater than $2.17 per gallon, the break-even price of sugar juice (Table 4). These switching threshold prices are calculated based on risk-free interest rates of 8.25 percent, 10-year plant life, an average ethanol market price of $2.17 per gallon taken from last seven years (2009–2015), and assuming the drift rate for the sugar price process is zero. We additionally run sensitivity analyses to explore if the planning horizon affects switching threshold prices. Results in Table 5 illustrate that optimal threshold prices increase as the length of the time horizon increases, in the full sample, implying that longer time horizons do not increase the expected returns for switching. Although, the optimal switching threshold prices are still greater than the break-even price of sugar juice, threshold prices fall as the length of planning horizon increases, using the subsample data. This shows the significant effect that volatility has on threshold prices. When volatility is higher, as in the subsample, switching appears advantageous as the time horizon expands, but when volatility is lower, as in the full sample, maintaining the status quo becomes more likely.
$P_s^{\ast} $
) are $6.54 and $5.07 per gallon, respectively, which are far greater than $2.17 per gallon, the break-even price of sugar juice (Table 4). These switching threshold prices are calculated based on risk-free interest rates of 8.25 percent, 10-year plant life, an average ethanol market price of $2.17 per gallon taken from last seven years (2009–2015), and assuming the drift rate for the sugar price process is zero. We additionally run sensitivity analyses to explore if the planning horizon affects switching threshold prices. Results in Table 5 illustrate that optimal threshold prices increase as the length of the time horizon increases, in the full sample, implying that longer time horizons do not increase the expected returns for switching. Although, the optimal switching threshold prices are still greater than the break-even price of sugar juice, threshold prices fall as the length of planning horizon increases, using the subsample data. This shows the significant effect that volatility has on threshold prices. When volatility is higher, as in the subsample, switching appears advantageous as the time horizon expands, but when volatility is lower, as in the full sample, maintaining the status quo becomes more likely.
Table 5. Switching Threshold Prices ($/gallon) for Ethanol and Sugar Juice under GBM

Effects of Planning Horizon and Sugar Price Drift Rates
We run sensitivity analyses to further calculate the threshold prices for alternative combinations of time horizons and drift rates. As presented on Table 2, point estimates of β for sugar are −0.01 and −0.021 in the full and subsample data. We estimated the baseline threshold prices assuming the drift rate of sugar price is zero, because β parameters on the sugar price series are not statistically significant. For the purposes of comparative statistics, we conducted the analysis with the assumption that the nonzero drift rates of the sugar price are 0.013 and 0.005 in full and subsample periods, respectively (see Table 3). With a positive sugar drift rate, switching threshold prices are $6.91 and $5.28 per gallon, which are not far from the results we obtained under a zero sugar drift rate. With the above positive drift rate of sugar prices, and 20- and 30-year planning horizons, the switching prices increase in the full sample data. However, threshold prices still fall in the subsample period to $4.24 and $3.80 per gallon (Table 5).
All threshold prices based on the subsample period are less than the results obtained using full sample data, irrespective of whether we use zero or positive sugar price drift rates. The low level of threshold prices is due to that fact that under full sample data the drift rate of ethanol is negative, implying that the expected rate of return from producing ethanol starts to decline with a negative drift rate. In addition, in the full sample data, the variance ratio of the prices of ethanol relative to sugar is higher, making the biorefinery start to switch away from a product that is highly volatile. Previous studies showed that higher relative price volatility will increase the value of flexibility and create increased investment in flexible technologies (Kulatilaka Reference Kulatilaka1988, Due and Hennessy Reference Du and Hennessy2008). However, we do not find that the higher relative price volatility of ethanol with respect to sugar prices induces switching to alternative mode of production, given the parameters used for our study. However, Vedenov, Duffield, and Wetzstein (Reference Vedenov, Duffield and Wetzstein2006) pointed out that effects of the volatility parameters of each product on threshold prices are indeterminate, implying that an increase in price volatility of ethanol and/or sugar may increase or decrease threshold prices (
![]() $P_s^{\ast} $
), depending on the magnitude of the two volatility ratios and on the sign of the two price correlations. Overall, the threshold switching prices are all above the break-even price of sugar juice (P
s
), indicating that switching to sugar juice production mode is still not economically optimal, given the drift rate of sugar and the planning horizons examined.
$P_s^{\ast} $
), depending on the magnitude of the two volatility ratios and on the sign of the two price correlations. Overall, the threshold switching prices are all above the break-even price of sugar juice (P
s
), indicating that switching to sugar juice production mode is still not economically optimal, given the drift rate of sugar and the planning horizons examined.
Effects of Ethanol Price Drift Rates
Comparative statistics analysis is also used to explore how threshold prices changes with a change in the drift rate of ethanol prices. Figure 3 depicts how option threshold prices change relative to ethanol price drift rates, keeping the volatility parameter of sugar constant, and taking the positive drift rates for sugar prices in Table 5. The horizontal line in Figure 3 depicts the break-even value of sugar juice, $2.17 per gallon. Our sensitivity analysis results indicate that switching to sugar mode is only economical at a point where the drift rate of ethanol prices is extremely negative. For example, when the drift rate falls to −0.15, the threshold price becomes $1.39 and $1.60 per gallon under the full and subsample periods, respectively. However, as the drift rate increasesFootnote 2 , threshold prices start to increase and reach the point where switching to sugar juice is no longer economical. At a drift rate of −0.05, in the full sample period, the threshold price is $2.17 per gallon. Note that the drift rate is a trend rate of growth in the market price of ethanol and sugar juice, and a positive and increasing drift rate is expected to improve the profitability of the ethanol and sugar juice investment.

Figure 3. Switching Threshold Prices Relative to Ethanol Drift Rates under GBM Process
The threshold prices in the two sample periods follow different optimal paths, and so does the rate at which threshold prices grow. To this end, our results show that flexibility is worth little as the profit from one output (ethanol) looks as if it dominates the others (sugar juice).
Effects of Different Stochastic Processes
In this section, we investigate the effects of different stochastic processes by comparing the switching threshold price obtained under MR processes relative to GBM. Although the parameter values of GBM and MR are not completely comparable. We present the threshold price results of MR in Table 6. Under MR, the baseline threshold prices are about $3.1 per gallon of ethanol, with both positive and zero drift rates of sugar prices (Table 6). This price is less than half the value obtained under the GMB model.
Table 6. Switching Threshold Prices ($/gallon) for Ethanol and Sugar Juice under MR

Further analysis using distant time horizon does little to affect the switching decision, given that the threshold prices are still greater than the break-even value of sugar juice (Table 6). The baseline results obtained under MR show that the switching threshold price follows distinct patterns compared to GBM. The results imply that the use of GBM significantly overestimates the value of the switching option due to the variance of GBM, which increases in proportion to time, unlike the bounded variance of a mean reverting process.
Effects of Ethanol and Sugar Price Correlations
So far we have used positive price correlations between ethanol and sugar: 0.17 and 0.25 from the full and subsample data period, implying that the two-price series are more likely to move in the same direction. We now run sensitivity analyses based on the MR process model to examine how threshold prices change for different values correlations between ethanol and sugar prices, along with three terminal periods: 10, 20, and 30 yearsFootnote 3 . Figure 4 plots the threshold switching prices versus the correlation between ethanol and sugar price processes under MR. Although Figure 4 illustrates that switching threshold prices fall rapidly as the correlation between the two prices diminishes in all three terminal periods, none of the threshold prices are equal to $2.17, to signal switching away from ethanol to industrial sugar production. Note again if the switching threshold is greater than $2.17/gal., the biorefinery owner may decide to switch from ethanol to sugar juice mode.

Figure 4. Switching Threshold Prices Relative to Correlation of Ethanol and Sugar Prices under MR Process
Figure 4 shows that switching threshold prices decrease when ethanol and sugar prices move independently. Conversely, they continue to increase if they become highly negatively correlated, implying that switching away from ethanol is not economical with all possible correlation values. The results imply that under the current ethanol and sugar markets and technological representation of a biorefinery, investing in a flexible biorefinery is not economically optimal. The future market conditions may change the fundamentals of investing in flexible biorefinery plants in the United States.
Relative Competitiveness of Beet-Based Ethanol
In this section, we explore the competitive position of beet ethanol relative to the conventional corn ethanol, assuming that the biorefinery plants are producing only ethanol and co-products. We first compute the Marshallian entry (W h ) and exit (W l ) gross margins of beet ethanol using W h = ω + δK, and exit gross margin, W l = ω − δK, assuming that the right-hand side is the annualized full cost of making and operating the investment. Here ω is the sum of all operating costs less beet feedstock cost, δ is the interest rate and K is the fixed capital. In our study, the value of ω and K are $0.514 and $3.25 per gallon, respectively. Thus, the full cost ω + δK serves as the entry trigger, and the nonbeet operating cost ω as the exit trigger gross margin threshold for making an investment decision. We find the entry and exit gross margins to be $0.84 and $0.20 per gallon, respectively. In this range, an idle firm does not invest, and an active firm does not exit. The ethanol refinery will generate a flow of operating profit equal to P − ω per period, where P is the firm's ethanol gross margin ($/gallon). It is apparent that investors will likely put forward the capital required to build and operate a plant if conversion margins are large enough. Margins are primarily determined by feedstock costs. Interested readers can refer Hossiso and Ripplinger (Reference Hossiso and Ripplinger2016) study for further analysis.
An instructive way to compare the competitive advantage of beet ethanol relative to conventional corn ethanol is to examine historical gross margin of corn ethanol to our model results. To help with the intuition, we consider first calculating the historical beet ethanol gross margin ($/gallon), taking past sugar beet and pulp prices. We then overlay the gross margins of corn and beet ethanol on the Marshallian entry and exit gross margins (Figure 5). We define beet ethanol gross margin as a sum of prices of ethanol and beet pulp minus beet price. Likewise, we define corn ethanol gross margin as sum of the prices of ethanol and distiller dried grain (DDG) less corn price. Figure 5 displays the gross margins of corn and beet ethanol overlaid on the Marshallian entry and exit gross marginsFootnote 4 .

Figure 5. Historical Beet and Corn Gross Margins Overlaid on Beet NPV Entry and Exit Trigger Margins
Figure 5 shows that the gross margins of the corn and beet ethanol tend to follow similar trends. However, the gross margins in a few time periods diverge, an indication of the variations in corn and beet feedstock prices. From 2000 to 2008, gross margins of corn ethanol were greater than that of beet before it fell in 2008 and 2009. The historical gross margins of beet ethanol are above our baseline Marshallian entry gross margin for many periods, an indication that there were few time periods that would have supported beet ethanol plant investment (Figure 5). Out of the 180 studied months, there are only 46 months that the Marshallian entry gross margin (0.84 $/gal) was greater than that of actual corn ethanol gross margins. Apparently, the time periods where beet margin was greater than that of corn were in 2008–2009, and after 2013, ethanol prices were above $2.00/gal. In part, the per-ton prices of beets fell from a historically high $67 in 2012 to an averaged $39 in 2013–2015. Overall, corn ethanol has a cost advantage over beet ethanol because of the relative advantage of the competitive pricing of corn over sugar beet feedstock. For example, from 2010–2015, the average gross margin for corn was $0.99, with beets at $0.92 per gallon.
However, Marshallian NPV entry trigger margins do not account for volatility and risk associated with price and costs. An NPV entry trigger margin at $0.84/gal would have signaled investments in energy beet ethanol in many time periods given that its value is greater than that of ethanol gross margins. On the exit side, several time periods would have supported a plant exit. It is apparent that narrow gross margins could tighten ethanol plant profitability, and in the long run, this condition could decrease the value of the ethanol plant.
To understand the relative cost advantages of U.S. beets and corn, and Brazilian sugarcane ethanol, we must first understand the share of each feedstock cost to ethanol production cost. A three-way comparison among Brazilian sugarcane, U.S. corn, and beet feedstock shows that a Brazilian sugarcane feedstock has the greatest cost advantage over the other feedstocks. Depending on the production year, for example, feedstock is 63% for U.S. beets (Wamisho, Ripplinger, and De Laporte Reference Wamisho, Ripplinger and De Laporte2015), 68% for U.S. corn (Iowa State University 2016), and 60% Brazilian sugarcane (UNICA 2010, Valdes Reference Valdes2011)Footnote 5 . To compare, the average 2005–2008 total cost of ethanol production for Brazilian sugarcane was $1.20 per gallon, corn ethanol $1.81, and beet ethanol $2.257 per gallon (Valdes Reference Valdes2011, Wamisho, Ripplinger, and De Laporte, Reference Wamisho, Ripplinger and De Laporte2015, Iowa State University 2016).
Looking forward, market and government policy factors including ethanol tax credits, mandates, and blend walls are critical to induce investment on beet ethanol in the U.S. biofuels industry. Regarding the market, the prices of ethanol and beet feedstock will be critical to determine the future of beet ethanol, most importantly as an octane enhancer complement with gasoline will likely continue induce demands, and any decrease in gasoline prices would result in an increase in ethanol for fuel blending. Conversely, as a substitute for gasoline, a fall in gasoline price reduces consumption of ethanol, as oil refiners become reluctant to blend the mandated volume of ethanol with gasoline. The net effect could depend on the relative strength of the two offsetting influences, measured via demand and supply elasticities of ethanol and gasoline (Pouliot and Babcock. Reference Pouliot and Babcock2014, Valdes, Hjort, and Seeley 2016).
For conventional corn ethanol, prices of corn declined almost by half from averaged $6.67 in 2012 to $3.65 per bushel in 2016, making feedstock cost cheaper to corn refineries. However, an ethanol plant profitability spreadsheet covering January 2015–July 2016 showed that net returns on overall costs for ethanol producers were negative for 12 out of the 16 months (Iowa State University (ISU) 2016). The fall in net return is largely attributed to the recent sharp decline in gasoline prices where ethanol prices followed suit. For example, from January 2015 to June 2016, the average ethanol price was $1.57 per gallon. Thus, given current ethanol market conditions, it is likely that the price of ethanol cannot cover the costs of capital, feedstock, and conversion of beet ethanol.
It is likely that the price of feedstock, and prices of ethanol and crude oil co-move in the U.S. fuel market, and any volatility in the prices of crude oil specifically affect investment in new beet ethanol. In July 2016, crude oil prices averaged $40 per barrel, the lowest level since 2009. This was more than 59 percent lower than the July 2009 average. In fact, oil prices may not rise to $100 per barrel in the near future, given the global oil supply and demand. Indeed, lower gasoline prices can affect U.S. ethanol trade because availability for exports depends largely on the amount of ethanol that is produced beyond the RFS2 (Valdes et al. 2016).
The ethanol blend wall is also likely to limit the future growth of corn ethanol, given that the market for conventional corn ethanol is approaching the current a blend wall (E-10) limit set by RFS2. In 2015, actual U.S. production of fuel ethanol reached a total of 14.8 bg, while that year, about 140.43 bg of gasoline were consumed, making ethanol volumetric share of total U.S. motor gasoline supply just greater than the 10 percent blend wall (E-10) limit (Energy Information Administration (EIA), 2016). In 2015, the statutory requirement for renewable fuel under RFS2 was 16.28 bg. Notwithstanding, in 2015 there was a fall in gasoline consumption, about 1.5 percent less than the record high of consumed in 2007 (EIA 2016). The fall in gasoline demand is partly attributed to increased fuel efficiency and decreased annual vehicle miles traveled (Valdes et al. 2016). Given the E-10 blend wall limit and corn ethanol production capacity, there will be a thin market for beet ethanol unless it is going to fill the advanced biofuel requirement category. However, the presence of flexible production option allows the flexible beet ethanol plants to easily switch to the production of sugar or vice versa, allowing a hedge against the uncertainty in gasoline prices, overall demand, and E-10 blend wall.
With respect to the ethanol tax credits and mandates, beet and corn ethanol are likely to compete in a differentiated ethanol market, should beet ethanol be designated as an advanced biofuel. Most importantly, beet ethanol plant investors would certainly benefit from a $1.01 per gallon tax credits for refiners blending cellulosic and advanced biofuels with gasoline. In addition to the tax credits, the advanced biofuel consumption mandates requirement set by RFS2 will critically determine the amount of advanced biofuel to be blended in transportation fuel. For 2016 and beyond, the mandates require one bgy of advanced biofuel to be blended into U.S. transportation fuel. Under the current market conditions, it is unlikely the U.S. biofuels industry will be able to produce advanced biofuel domestically to meet the expanding RFS2 advanced biofuel mandates because investment in advanced biofuel plants lags behind schedule (Schnepf and Yacobucci Reference Schnepf and Yacobucci2013). Thus far, a large portion of the advanced biofuel mandates has been filled by imported Brazilian sugarcane ethanol, even when domestic production of total ethanol is greater than consumption. Beet ethanol can potentially be substituted for imported Brazilian sugarcane ethanol and fulfill the continued expansion of advanced biofuel requirement, should the EPA designate beet ethanol as an advanced biofuel.
Conclusion and Implication of the Findings
This study develops a real-options approach to compute the optimal switching threshold prices in a flexible biorefinery plant that has the option to produce sugar juice or ethanol. We use GBM to describe the dynamic processes of the underlying uncertain state variables and the switching option, and later compare results from GBM with MR. The main result of the analysis is that the threshold prices are higher than the break-even price of sugar juice for various scenario across all the sample periods. Given the ethanol price patterns and parameters we obtained from historical ethanol and sugar prices, the study concludes that switching from ethanol to sugar juice is not an economically sound decision. However, further sensitivity analysis shows that switching to sugar juice production is optimal if the drift rate of ethanol is extremely low.
Relative to a MR, threshold prices from GBM are biased upward in all sensitivity analysis runs. In addition, analysis based on MR shows that threshold prices change insignificantly with a change in planning horizons and drift rates of sugar price processes. We also found that higher ethanol price volatility relative to sugar prices does not induce switching to sugar production. Should prices of sugar and ethanol begin to decouple as the markets for energy beet sugar juice and ethanol develops, future correlation may have an important role in ethanol and sugar market dynamics. Finally, results show that the model predictions are sensitive to assumptions about the stochastic evolution processes of ethanol and sugar prices.
In summary, key challenges potential beet biofuel investors are likely to face are large upfront costs and investment uncertainty regarding availability and cost of beet feedstock, and logistic and policy uncertainty with respect to designating beet ethanol as advanced biofuel. In addition, it is likely that the recent fall in price of crude oil and thus ethanol over time could be a disincentive for entry of new beet ethanol plants in the mid- to long term, unless there are government subsidies in the form of tax credits and volumetric mandates requirements. However, investment in flexible plants would provide a firm with a hedge against demand uncertainty, and each product serves as natural hedge in ethanol and sugar market, depending on the relative price volatility of the two products.
Along with market factors, existing U.S. ethanol policies including mandates, tax credits, and blend wall limits, potentially determine investment in beet ethanol. The existing 10 percent (E10) blend wall limit becomes an obstacle for future ethanol capacity expansion given that actual ethanol production is already greater than the physical blend limit of the U.S. transportation fuel, implying that a future market for new ethanol will become difficult unless investment in infrastructure for E-15 and E-85 is made to accommodate additional ethanol. Conversely, investments in advanced biofuel and cellulosic ethanol plants lag behind the schedule laid out in the RFS2 mandates, therefore supporting investments in flexible beet ethanol could potentially fill the domestic market for advanced biofuel.
While our empirical analysis has certainly advanced our understanding of the flexible ethanol plant, an important feasibility and policy question is: What factors are critical to draw investments in flexible ethanol plants? We believe that beyond the market factors, government ethanol subsidy policies in the form of tax credits, creating a guaranteed market, government research and development (R&D), grants, and loan guarantees could help promote the investment in flexible beet ethanol. Thus far, investment in the U.S. ethanol industry is largely driven by various government incentives and production and consumption mandates provision (Epplin et al. Reference Epplin, Clark, Roberts and Hwang2007, Babcock, Marette and Tréguer Reference Babcock, Marette and Tréguer2010, Wetzstein Reference Wetzstein2010, Schmit et al. Reference Schmit, Luo and Conrad2011, Yi, Lin and Thome 2015). For example, Schmit et al. (Reference Schmit, Luo and Conrad2011) found that in the absence of ethanol policies, much of the recent rush in ethanol plant expansion would have not existed. Yi, Lin and Thome (2015) found that the RFS is a critically important policy for supporting the sustainability of corn-based fuel ethanol production, and that investment and entry subsidies are more effective than production subsidies.
From a policy perspective, our results likely offer important insights and contributions to the empirical literature. Future growth in biofuel production is likely to come from a variety of alternative feedstock sources to corn starch, including cellulosic, agricultural waste, and biomass, to meet the RFS2 mandates of 21 bg of advanced biofuel. The introduction of flexible beet ethanol plants would give an extra competitive edge for the U.S. biofuel industry and enable firms to choose an optimal combination of sugar juice and ethanol production, depending on the predominant economic conditions. The commercialization of flexible biorefineries in the United States is possible, as long as market conditions, technology choices, and policy support for biofuel and sugar products are favorable.












