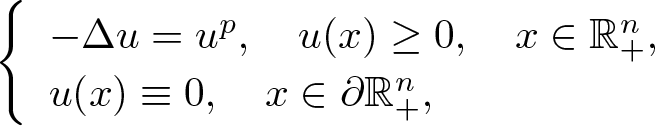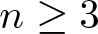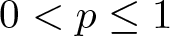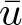1. Introduction
There are some typical nonlinear Liouville theorems about the Lane–Emden equation
which go back to J. Serrin in the 1970s. In 1981, Gidas and Spruck [Reference Gidas and Spruck11] proved that equation (1.1) has no nontrivial non-negative classical solution if ![]() $n\geq2$ and
$n\geq2$ and  $p \lt \frac{n+2}{(n-2)_+}$.
$p \lt \frac{n+2}{(n-2)_+}$.
However, a full answer to the existence of classical solutions for Lane–Emden equation (1.1) is currently not available for proper subdomains of ![]() $\mathbb{R}^n$. This is so even for the Dirichlet problem
$\mathbb{R}^n$. This is so even for the Dirichlet problem
 \begin{equation}
\left\{
\begin{array}{ll}
-\Delta u=u^{p},\quad u(x)\geq0,~x\in\mathbb{R}^n_+, \\
u(x)\equiv0,\quad x\in\partial\mathbb{R}^n_+.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
-\Delta u=u^{p},\quad u(x)\geq0,~x\in\mathbb{R}^n_+, \\
u(x)\equiv0,\quad x\in\partial\mathbb{R}^n_+.
\end{array}
\right.
\end{equation} where ![]() $\mathbb{R}^n_+$ is the half space
$\mathbb{R}^n_+$ is the half space
despite its long history and the large number of works on that problem, see e.g. [Reference Chen, Lin and Zou5–Reference Dupaigne, Sirakov and Souplet7, Reference Fang and Chen9, Reference Gidas and Spruck10].
Since the half space is the simplest unbounded domain with an unbounded boundary and performing a blow-up close to the boundary for some elliptic equations in a smooth domain leads to the Lane–Emden equation in a half space, studying the elliptic equations in half space is very meaningful.
Combining moving planes argument with Kelvin transform, Gidas and Spruck [Reference Gidas and Spruck10] reduces the Dirichlet problem (P) to the one-dimensional case and then proved that (P) has no solutions in half space ![]() $\mathbb{R}^n_+$, provided
$\mathbb{R}^n_+$, provided  $1 \lt p \leq \frac{n+2}{n-2}$.
$1 \lt p \leq \frac{n+2}{n-2}$.
The question of existence of bounded solutions of the Dirichlet problem for (P) in half space was fully answered by Chen et al. [Reference Chen, Lin and Zou5]. By selecting a good auxiliary function involving derivatives of u and using convexity considerations, the authors proved that (P) has no bounded solutions for any ![]() $1 \lt p \lt +\infty$.
$1 \lt p \lt +\infty$.
We notice that the condition p > 1 is indispensable in these Liouville-type theorems for the Lane–Emden equation [Reference Chen, Lin and Zou5–Reference Dupaigne, Sirakov and Souplet7, Reference Fang and Chen9, Reference Gidas and Spruck10] in half space and fractional Lane–Emden equation [Reference Chen, Fang and Yang3] in half space. To our knowledge, the non-existence of non-negative solutions of (P) in ![]() $\mathbb{R}^n_+$ is completely open in the sublinear range
$\mathbb{R}^n_+$ is completely open in the sublinear range ![]() $0 \lt p \leq1$. Here, we study this range and prove that
$0 \lt p \leq1$. Here, we study this range and prove that
Theorem 1.1 Assume that ![]() $n\geq3$ and
$n\geq3$ and ![]() $0 \lt p \leq 1$. If
$0 \lt p \leq 1$. If  $u\in C^{2}(\mathbb{R}^n_+)\cap C(\overline{\mathbb{R}^n_+})$ is a non-negative solution of (P), then
$u\in C^{2}(\mathbb{R}^n_+)\cap C(\overline{\mathbb{R}^n_+})$ is a non-negative solution of (P), then ![]() $u \equiv 0$.
$u \equiv 0$.
Remark 1.2. The author believe that using a process similar to proving Theorem 1.1, the Liouville result also holds for n = 2. This requires changing the fundamental solution of ![]() $-\Delta$ to
$-\Delta$ to  $\ln\frac{1}{|x|}$, the comparison function ϕ defined in (3.10) to
$\ln\frac{1}{|x|}$, the comparison function ϕ defined in (3.10) to ![]() $x_2^r+\ln|x|$ for
$x_2^r+\ln|x|$ for ![]() $r\in(0,1)$, and making some corresponding adjustments.
$r\in(0,1)$, and making some corresponding adjustments.
Very recently, Montoro, Muglia, and Sciunzi [Reference Montoro, Muglia and Sciunzi13, Reference Montoro, Muglia and Sciunzi14] provided a classification result for positive solutions to (P) for ![]() $n\geq1$ in singular case:
$n\geq1$ in singular case: ![]() $p \lt -1$ and non-existence of positive solutions to (P) for
$p \lt -1$ and non-existence of positive solutions to (P) for ![]() $n\geq1$ in the case:
$n\geq1$ in the case: ![]() $-1\leq p \lt 0$. Theorem 1.1 together with [Reference Gidas and Spruck10] and the results in [Reference Montoro, Muglia and Sciunzi13, Reference Montoro, Muglia and Sciunzi14] provide a complete description of the solution to the Lane–Emden problem in
$-1\leq p \lt 0$. Theorem 1.1 together with [Reference Gidas and Spruck10] and the results in [Reference Montoro, Muglia and Sciunzi13, Reference Montoro, Muglia and Sciunzi14] provide a complete description of the solution to the Lane–Emden problem in ![]() $\mathbb{R}^n_+$ (P).
$\mathbb{R}^n_+$ (P).
The main innovation of this article:
To use the comparison principle (see § 2), the low bound of the Lipschitz coefficient
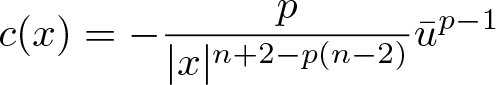 \begin{equation*}
c(x)=-\frac{p}{|x|^{n+2-p(n-2)}}\bar{u}^{p-1}
\end{equation*}
\begin{equation*}
c(x)=-\frac{p}{|x|^{n+2-p(n-2)}}\bar{u}^{p-1}
\end{equation*} is required. Due to p < 1, we need some low bound of ![]() $\bar{u}$ for the sublinear problem in half space. Different with the whole space problem, for
$\bar{u}$ for the sublinear problem in half space. Different with the whole space problem, for ![]() $|x|$ large,
$|x|$ large,  $C\frac{1}{|x|^{n-2}}$ is only the upper bound of the Kelvin transformation
$C\frac{1}{|x|^{n-2}}$ is only the upper bound of the Kelvin transformation ![]() $\bar{u}$ but not the low bound for the Dirichlet problem on half space.
$\bar{u}$ but not the low bound for the Dirichlet problem on half space.
To overcome this difficulty, by establishing an equivalent integral equation, we obtain a lower bound  $\bar{u}(x)\geq C\frac{x_n}{|x|^{n}}$ for
$\bar{u}(x)\geq C\frac{x_n}{|x|^{n}}$ for ![]() $|x|$ large. Based on the suitable lower bound of
$|x|$ large. Based on the suitable lower bound of ![]() $\bar{u}$, we find a new comparison function
$\bar{u}$, we find a new comparison function  $\phi(x)=\frac{1}{|x|^q}+x_n^r$ and then use the maximum principle based on comparisons to find that u only depends on xn. Then, based on this and the equivalent integral equation, we prove the non-existence of non-negative solutions.
$\phi(x)=\frac{1}{|x|^q}+x_n^r$ and then use the maximum principle based on comparisons to find that u only depends on xn. Then, based on this and the equivalent integral equation, we prove the non-existence of non-negative solutions.
2. Preliminaries
Proposition 2.1. (Strong Maximum Principle, [Reference Gilbarg and Trudinger12])
Consider a domain ![]() $\Omega\subset\mathbb{R}^n$ and define
$\Omega\subset\mathbb{R}^n$ and define
 \begin{equation*}L = -\Delta +\sum\limits_{i}b_i\partial_i + c,\end{equation*}
\begin{equation*}L = -\Delta +\sum\limits_{i}b_i\partial_i + c,\end{equation*} where bi and c are bounded on Ω. Suppose that ![]() $u\in C^2(\Omega) \cap C(\overline{\Omega})$ satisfies
$u\in C^2(\Omega) \cap C(\overline{\Omega})$ satisfies ![]() $Lu \geq 0$ and
$Lu \geq 0$ and ![]() $u \geq 0$ in Ω. If u vanishes at some point in Ω, then
$u \geq 0$ in Ω. If u vanishes at some point in Ω, then ![]() $u \equiv 0$ in Ω. In particular, if there exists a point on
$u \equiv 0$ in Ω. In particular, if there exists a point on ![]() $\partial\Omega$, where u > 0, then u > 0 in Ω.
$\partial\Omega$, where u > 0, then u > 0 in Ω.
Proposition 2.2. (Hopf’s Lemma, § 9.5 Lemma 1 in [Reference Evans8])
Let B be a ball in ![]() $\mathbb{R}^n$ and consider the elliptic operator
$\mathbb{R}^n$ and consider the elliptic operator
where c is bounded in B. Assume further that ![]() $u\in C^2(B) \cap C^1(\overline{B})$ satisfies
$u\in C^2(B) \cap C^1(\overline{B})$ satisfies ![]() $Lu \geq 0$ in B. If there exists
$Lu \geq 0$ in B. If there exists ![]() $x\in \partial B$ such that
$x\in \partial B$ such that
then one has  $\frac{\partial u}{\partial\nu}(x^0) \lt 0$ for any outward pointing directional derivative ν and, in particular,
$\frac{\partial u}{\partial\nu}(x^0) \lt 0$ for any outward pointing directional derivative ν and, in particular, ![]() $\nabla u(x^0) \neq 0$.
$\nabla u(x^0) \neq 0$.
Proposition 2.3. (Comparison Principle)
Assume that Ω is a domain. Let ϕ be a positive function on ![]() $\bar{\Omega}$ satisfying
$\bar{\Omega}$ satisfying
Assume that ![]() $w\in C^2(\Omega) \cap C(\bar{\Omega})$ solves
$w\in C^2(\Omega) \cap C(\bar{\Omega})$ solves
 \begin{equation}
\left\{
\begin{array}{ll}
-\Delta w+c(x)w\geq 0,~~x\in\Omega, \\
w\geq 0,\quad x\in\partial\Omega.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
-\Delta w+c(x)w\geq 0,~~x\in\Omega, \\
w\geq 0,\quad x\in\partial\Omega.
\end{array}
\right.
\end{equation}If
and
 \begin{equation}
\liminf\limits_{|x|\to\infty, x\in\Omega}\frac{w(x)}{\phi(x)} \geq 0,
\end{equation}
\begin{equation}
\liminf\limits_{|x|\to\infty, x\in\Omega}\frac{w(x)}{\phi(x)} \geq 0,
\end{equation} then ![]() $w\geq 0$ in Ω.
$w\geq 0$ in Ω.
Proof. The Comparison Principle can be found in [Reference Chen and Li4, Theorem 4.1]. For the convenience of readers, we provide its proof.
Suppose that there is a point ![]() $x\in\Omega$ such that
$x\in\Omega$ such that ![]() $w(x) \lt 0$. Let
$w(x) \lt 0$. Let  $\tilde{w}(x)=\frac{w(x)}{\phi(x)}$. By
$\tilde{w}(x)=\frac{w(x)}{\phi(x)}$. By ![]() $\phi(x) \gt 0$ and condition (2.2),
$\phi(x) \gt 0$ and condition (2.2), ![]() $\tilde{w}$ has a minimum point
$\tilde{w}$ has a minimum point ![]() $x^o\in\Omega$ such that
$x^o\in\Omega$ such that ![]() $\tilde{w}(x^o) \lt 0$. By straight calculation,
$\tilde{w}(x^o) \lt 0$. By straight calculation,
 \begin{equation}
-\Delta \tilde{w}(x)=2\nabla \tilde{w}\cdot\frac{\nabla\phi}{\phi}+\left(-\Delta w(x)+\frac{\Delta\phi}{\phi}w\right)\frac{1}{\phi}.
\end{equation}
\begin{equation}
-\Delta \tilde{w}(x)=2\nabla \tilde{w}\cdot\frac{\nabla\phi}{\phi}+\left(-\Delta w(x)+\frac{\Delta\phi}{\phi}w\right)\frac{1}{\phi}.
\end{equation} On the one hand, since xo is the minimum point of ![]() $\tilde{w}$, then
$\tilde{w}$, then
Then by (2.3), we get
 \begin{equation}-\Delta w(x^o)+\frac{\Delta\phi}{\phi}w(x^o)\leq 0.\end{equation}
\begin{equation}-\Delta w(x^o)+\frac{\Delta\phi}{\phi}w(x^o)\leq 0.\end{equation} On the other hand, by ![]() $w(x^o) \lt 0$ and the assumption of the proposition,
$w(x^o) \lt 0$ and the assumption of the proposition,
 \begin{equation*}-\Delta w(x^o)+\frac{\Delta\phi}{\phi}w(x^o)\geq -\Delta w(x^o)+\lambda(x^o)w(x^o) \gt -\Delta w(x^o)+c(x^o)w(x^o)\geq0.\end{equation*}
\begin{equation*}-\Delta w(x^o)+\frac{\Delta\phi}{\phi}w(x^o)\geq -\Delta w(x^o)+\lambda(x^o)w(x^o) \gt -\Delta w(x^o)+c(x^o)w(x^o)\geq0.\end{equation*}This contradicts (2.4).
Remark 2.4. From the proof of proposition 2.3 (Comparison Principle), one can see that condition (2.1) is required only at the points where ![]() $\tilde{w}$ attains its minimum.
$\tilde{w}$ attains its minimum.
The idea in the following arguments is similar to that in the proof of [Reference Chen, Fang and Yang3, Theorem 4.1].
Proposition 2.5. Assume that  $u\in C^{2}(\mathbb{R}^n_+)\cap C(\overline{\mathbb{R}^n_+})$ is a positive solution of problem (P). Then, u is also a solution of integral equation
$u\in C^{2}(\mathbb{R}^n_+)\cap C(\overline{\mathbb{R}^n_+})$ is a positive solution of problem (P). Then, u is also a solution of integral equation
 \begin{equation}
u(x) =\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy.
\end{equation}
\begin{equation}
u(x) =\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy.
\end{equation} Here, ![]() $G(x, y)$ is the Green function of
$G(x, y)$ is the Green function of ![]() $-\Delta$ on half space
$-\Delta$ on half space ![]() $\mathbb{R}^n_+$:
$\mathbb{R}^n_+$:
 \begin{equation*}G(x,y)=c_n\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{(|x-y|^2+4x_ny_n)^{\frac{n-2}{2}}}\right],~~c_n = \frac{\Gamma(\frac{n}{2}-1)}{4\pi^{\frac{n}{2}}}.\end{equation*}
\begin{equation*}G(x,y)=c_n\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{(|x-y|^2+4x_ny_n)^{\frac{n-2}{2}}}\right],~~c_n = \frac{\Gamma(\frac{n}{2}-1)}{4\pi^{\frac{n}{2}}}.\end{equation*}Proof. Let u be a positive solution of (P). First, we show that
 \begin{equation}
\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy \lt +\infty.
\end{equation}
\begin{equation}
\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy \lt +\infty.
\end{equation}Set
 \begin{equation*}v_R(x)=\int_{B_R(P_R)}G_R(x,y)u^{p}(y)dy,\end{equation*}
\begin{equation*}v_R(x)=\int_{B_R(P_R)}G_R(x,y)u^{p}(y)dy,\end{equation*} where ![]() $G_R(x, y)$ is the Green’s function on
$G_R(x, y)$ is the Green’s function on ![]() $B_R(P_R)$, and
$B_R(P_R)$, and ![]() $P_R =(0, \cdot\cdot\cdot, 0, R)$,
$P_R =(0, \cdot\cdot\cdot, 0, R)$,
 \begin{equation*}G_R(x,y)=c_n\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{\left(|x-y|^2+\left(R-\frac{|x-P_R|^2}{R}\right)\left(R-\frac{|y-P_R|^2}{R}\right)\right)^{\frac{n-2}{2}}}\right].\end{equation*}
\begin{equation*}G_R(x,y)=c_n\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{\left(|x-y|^2+\left(R-\frac{|x-P_R|^2}{R}\right)\left(R-\frac{|y-P_R|^2}{R}\right)\right)^{\frac{n-2}{2}}}\right].\end{equation*} Obviously, the Green’s function GR on ![]() $B_R(P_R)$ converges pointwise and monotonically to the Green’s function G on
$B_R(P_R)$ converges pointwise and monotonically to the Green’s function G on ![]() $\mathbb{R}^n_+$. From the assumption on u, one can see that, for each R > 0,
$\mathbb{R}^n_+$. From the assumption on u, one can see that, for each R > 0, ![]() $v_R(x)$ is well-defined and is continuous. Moreover,
$v_R(x)$ is well-defined and is continuous. Moreover,
 \begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta v_R(x)=u^p(x),~~x\in B_R(P_R), \\
v_R(x)= 0,\quad x\notin B_R(P_R).
\end{array}
\right.
\end{equation*}
\begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta v_R(x)=u^p(x),~~x\in B_R(P_R), \\
v_R(x)= 0,\quad x\notin B_R(P_R).
\end{array}
\right.
\end{equation*} Let ![]() $w_R(x) = u(x)-v_R(x)$, then
$w_R(x) = u(x)-v_R(x)$, then
 \begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta w_R(x)=0,~~x\in B_R(P_R), \\
w_R(x)\geq 0,\quad x\notin B_R(P_R).
\end{array}
\right.
\end{equation*}
\begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta w_R(x)=0,~~x\in B_R(P_R), \\
w_R(x)\geq 0,\quad x\notin B_R(P_R).
\end{array}
\right.
\end{equation*}Now, by the Maximum Principle [Reference Gilbarg and Trudinger12], we derive
Then, letting ![]() $R\to\infty$, we arrive at
$R\to\infty$, we arrive at
 \begin{equation*} u(x) \geq\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy:=v(x),\end{equation*}
\begin{equation*} u(x) \geq\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy:=v(x),\end{equation*}and thus, (2.6) holds. Here, v(x) satisfies
 \begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta v(x)=u^p(x),~~x\in \mathbb{R}^n_+, \\
v(x)= 0,\quad x\notin \mathbb{R}^n_+.
\end{array}
\right.
\end{equation*}
\begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta v(x)=u^p(x),~~x\in \mathbb{R}^n_+, \\
v(x)= 0,\quad x\notin \mathbb{R}^n_+.
\end{array}
\right.
\end{equation*} Setting ![]() $w =u -v$, we have
$w =u -v$, we have
 \begin{equation}
\left\{
\begin{array}{ll}
-\Delta w(x)=0,~~w(x)\geq0,~~x\in \mathbb{R}^n_+, \\
w(x)= 0,\quad x\notin \mathbb{R}^n_+.
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
-\Delta w(x)=0,~~w(x)\geq0,~~x\in \mathbb{R}^n_+, \\
w(x)= 0,\quad x\notin \mathbb{R}^n_+.
\end{array}
\right.
\end{equation}Based on Boundary Harnack Inequality [Reference Ancona1, Reference Bass and Burdzy2], the uniqueness of harmonic functions on half spaces is well known: either
or there is a constant c, such that
We will derive a contradiction in the latter case. In fact, in this case, we have
Denote ![]() $x =(x', x_n)$,
$x =(x', x_n)$, ![]() $y =(y', y_n) \in \mathbb{R}^{n-1} \times (0, +\infty)$. It follows from (2.8) that, for each fixed x and for sufficiently large R,
$y =(y', y_n) \in \mathbb{R}^{n-1} \times (0, +\infty)$. It follows from (2.8) that, for each fixed x and for sufficiently large R,
 \begin{align*}
u(x)& \geq v(x)=\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy\geq c\int_{\mathbb{R}^n_+}G(x,y)y_n^{p}dy\\ & \geq c\int_R^{+\infty}y_n^pdy_n\int_{\mathbb{R}^{n-1}}G(x,y)dy'.
\end{align*}
\begin{align*}
u(x)& \geq v(x)=\int_{\mathbb{R}^n_+}G(x,y)u^{p}(y)dy\geq c\int_{\mathbb{R}^n_+}G(x,y)y_n^{p}dy\\ & \geq c\int_R^{+\infty}y_n^pdy_n\int_{\mathbb{R}^{n-1}}G(x,y)dy'.
\end{align*}Notice that
 \begin{align}
& \int_{\mathbb{R}^{n-1}}G(x,y)dy'\\ & \quad =\int_{\mathbb{R}^{n-1}}\left[\frac{1}{(|x'-y'|^2+|x_n-y_n|^2)^{\frac{n-2}{2}}}-\frac{1}{(|x'-y'|^2+|x_n+y_n|^2)^{\frac{n-2}{2}}}\right]dy' \nonumber\\
& \quad = \int_{\mathbb{R}^{n-1}}\left[\frac{1}{(|x'-y'|^2)^{\frac{n-2}{2}}}-\frac{1}{(|x'-y'|^2+|x_n+y_n|^2)^{\frac{n-2}{2}}}\right]dy'\nonumber \\
& \quad \quad -\int_{\mathbb{R}^{n-1}}\left[\frac{1}{(|x'-y'|^2)^{\frac{n-2}{2}}}-\frac{1}{(|x'-y'|^2+|x_n-y_n|^2)^{\frac{n-2}{2}}}\right]dy'\nonumber \\
& \quad = C\left(|x_n+y_n|-|y_n-x_n|\right),
\end{align}
\begin{align}
& \int_{\mathbb{R}^{n-1}}G(x,y)dy'\\ & \quad =\int_{\mathbb{R}^{n-1}}\left[\frac{1}{(|x'-y'|^2+|x_n-y_n|^2)^{\frac{n-2}{2}}}-\frac{1}{(|x'-y'|^2+|x_n+y_n|^2)^{\frac{n-2}{2}}}\right]dy' \nonumber\\
& \quad = \int_{\mathbb{R}^{n-1}}\left[\frac{1}{(|x'-y'|^2)^{\frac{n-2}{2}}}-\frac{1}{(|x'-y'|^2+|x_n+y_n|^2)^{\frac{n-2}{2}}}\right]dy'\nonumber \\
& \quad \quad -\int_{\mathbb{R}^{n-1}}\left[\frac{1}{(|x'-y'|^2)^{\frac{n-2}{2}}}-\frac{1}{(|x'-y'|^2+|x_n-y_n|^2)^{\frac{n-2}{2}}}\right]dy'\nonumber \\
& \quad = C\left(|x_n+y_n|-|y_n-x_n|\right),
\end{align}where
 \begin{equation*}C=\int_{\mathbb{R}^{n-1}}\left(\frac{1}{|\xi|^{n-2}}-\frac{1}{(|\xi|^2+1)^{\frac{n-2}{2}}}\right)d\xi\in(0,+\infty).\end{equation*}
\begin{equation*}C=\int_{\mathbb{R}^{n-1}}\left(\frac{1}{|\xi|^{n-2}}-\frac{1}{(|\xi|^2+1)^{\frac{n-2}{2}}}\right)d\xi\in(0,+\infty).\end{equation*} Therefore, for ![]() $x_n \lt R$, we get
$x_n \lt R$, we get
 \begin{equation*}\nonumber
u(x)\geq cx_n\int_R^{+\infty}y_n^pdy_n=+\infty,
\end{equation*}
\begin{equation*}\nonumber
u(x)\geq cx_n\int_R^{+\infty}y_n^pdy_n=+\infty,
\end{equation*} which is a contradiction. Therefore, we must have ![]() $w\equiv0$, i.e., (2.5) holds.
$w\equiv0$, i.e., (2.5) holds.
3. Non-existence of positive solutions in the half space  $\mathbb{R}^n_+$
$\mathbb{R}^n_+$
We will employ the method of moving planes to prove the radial symmetry of u. However, without any decay conditions on u, we are not able to carry the method of moving planes on u directly. To overcome this difficulty, we employ the Kelvin transformation of u centred at ![]() $x^o\in\partial\mathbb{R}^n_+$,
$x^o\in\partial\mathbb{R}^n_+$,
 \begin{equation*}\bar{u}_{x^o}(x) = \frac{1}{|x-x^o|^{n-2}}u\left(\frac{x-x^o}{|x-x^o|^2}+x^o\right),~~\forall x \in \mathbb{R}^n\setminus\{x^o\}.\end{equation*}
\begin{equation*}\bar{u}_{x^o}(x) = \frac{1}{|x-x^o|^{n-2}}u\left(\frac{x-x^o}{|x-x^o|^2}+x^o\right),~~\forall x \in \mathbb{R}^n\setminus\{x^o\}.\end{equation*} Specifically, let ![]() $\bar{u}$ be the Kelvin transformation of u centred at the original point
$\bar{u}$ be the Kelvin transformation of u centred at the original point
 \begin{equation*}\bar{u}(x) = \frac{1}{|x|^{n-2}}u\left(\frac{x}{|x|^2}\right),~~\forall x \in \mathbb{R}^n\setminus\{0\}.\end{equation*}
\begin{equation*}\bar{u}(x) = \frac{1}{|x|^{n-2}}u\left(\frac{x}{|x|^2}\right),~~\forall x \in \mathbb{R}^n\setminus\{0\}.\end{equation*}Clearly,
 \begin{equation}\overline u(x)=O\left(\frac1{\vert x\vert^{n-2}}\right),\quad\vert x\vert\rightarrow\infty.\end{equation}
\begin{equation}\overline u(x)=O\left(\frac1{\vert x\vert^{n-2}}\right),\quad\vert x\vert\rightarrow\infty.\end{equation} Let u be the solution of (P). By direct calculation, the Kelvin transform ![]() $\bar{u}$ satisfies the equation
$\bar{u}$ satisfies the equation
 \begin{equation}
\left\{
\begin{array}{ll}
-\Delta\bar{u}=\frac{\bar{u}^{p}}{|x|^\tau},
~~x\in\mathbb{R}^n_+, \\
\bar{u}(x)\equiv0,\quad x\in\partial\mathbb{R}^n_+,
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{ll}
-\Delta\bar{u}=\frac{\bar{u}^{p}}{|x|^\tau},
~~x\in\mathbb{R}^n_+, \\
\bar{u}(x)\equiv0,\quad x\in\partial\mathbb{R}^n_+,
\end{array}
\right.
\end{equation} where ![]() $\tau=n+2-p(n-2)$.
$\tau=n+2-p(n-2)$.
For any real number λ, let
be the plane perpendicular to the ![]() $x_1$-axis. Let
$x_1$-axis. Let ![]() $\Sigma_{\lambda}$ be the region to the left of the plane Tλ
$\Sigma_{\lambda}$ be the region to the left of the plane Tλ
Denote
Set
According to equation (3.2),
 \begin{equation}
-\Delta w_\lambda(x)=\frac{\bar{u}^{p}(x^\lambda)}{|x^\lambda|^\tau}-\frac{\bar{u}^{p}(x)}{|x|^\tau}=\frac{1}{|x|^\tau}(\bar{u}^p(x^\lambda)-\bar{u}^p(x))+\bar{u}^p(x^\lambda)\left(\frac{1}{|x^\lambda|^\tau}-\frac{1}{|x|^\tau}\right).
\end{equation}
\begin{equation}
-\Delta w_\lambda(x)=\frac{\bar{u}^{p}(x^\lambda)}{|x^\lambda|^\tau}-\frac{\bar{u}^{p}(x)}{|x|^\tau}=\frac{1}{|x|^\tau}(\bar{u}^p(x^\lambda)-\bar{u}^p(x))+\bar{u}^p(x^\lambda)\left(\frac{1}{|x^\lambda|^\tau}-\frac{1}{|x|^\tau}\right).
\end{equation} For ![]() $x\in\Sigma_\lambda$ and
$x\in\Sigma_\lambda$ and ![]() $\lambda\leq0$, we have
$\lambda\leq0$, we have ![]() $|x^\lambda|\leq |x|$ and
$|x^\lambda|\leq |x|$ and
 \begin{equation}
-\Delta w_\lambda(x)\geq\frac{p}{|x|^\tau}\xi_\lambda^{p-1}w_\lambda(x),
\end{equation}
\begin{equation}
-\Delta w_\lambda(x)\geq\frac{p}{|x|^\tau}\xi_\lambda^{p-1}w_\lambda(x),
\end{equation} where ![]() $\xi_\lambda(x)$ is between
$\xi_\lambda(x)$ is between ![]() $\bar{u}(x^\lambda)$ and
$\bar{u}(x^\lambda)$ and ![]() $\bar{u}(x)$. For
$\bar{u}(x)$. For ![]() $0 \lt p\leq1$, if
$0 \lt p\leq1$, if ![]() $\bar{u}(x^\lambda)\leq\bar{u}(x)$, then
$\bar{u}(x^\lambda)\leq\bar{u}(x)$, then
 \begin{equation*}\frac{p}{|x|^\tau}\xi_\lambda^{p-1}w_\lambda(x)\geq \frac{p}{|x|^\tau}\bar{u}(x^\lambda)^{p-1}w_\lambda(x).\end{equation*}
\begin{equation*}\frac{p}{|x|^\tau}\xi_\lambda^{p-1}w_\lambda(x)\geq \frac{p}{|x|^\tau}\bar{u}(x^\lambda)^{p-1}w_\lambda(x).\end{equation*}Define
 \begin{equation*}
c(x)=-\frac{p}{|x|^\tau}\bar{u}(x^\lambda)^{p-1}.
\end{equation*}
\begin{equation*}
c(x)=-\frac{p}{|x|^\tau}\bar{u}(x^\lambda)^{p-1}.
\end{equation*} Assume ![]() $\lambda\leq0$,
$\lambda\leq0$, ![]() $x\in \Sigma_\lambda\setminus\{0^\lambda\}$ such that
$x\in \Sigma_\lambda\setminus\{0^\lambda\}$ such that ![]() $w_\lambda(x) \leq 0$. Then,
$w_\lambda(x) \leq 0$. Then,
Lemma 3.1. For ![]() $|x|$ large,
$|x|$ large,
 \begin{equation}
\bar{u}(x)\geq C\frac{x_n}{|x|^{n}}
\end{equation}
\begin{equation}
\bar{u}(x)\geq C\frac{x_n}{|x|^{n}}
\end{equation}and
 \begin{equation}
0 \gt c(x) \gt -\frac{Cx_n^{p-1}}{|x|^{2(p+1)}},
\end{equation}
\begin{equation}
0 \gt c(x) \gt -\frac{Cx_n^{p-1}}{|x|^{2(p+1)}},
\end{equation}where the constant C > 0 is independent of x and λ.
Proof. For ![]() $y\in B_1(2e_n)$, we have
$y\in B_1(2e_n)$, we have ![]() $u^p(y)\geq C$. Denote
$u^p(y)\geq C$. Denote ![]() $x^*=(x',-x_n)$, for
$x^*=(x',-x_n)$, for ![]() $|x| \lt 1$, by (2.5),
$|x| \lt 1$, by (2.5),
 \begin{align}
u(x)=&c_n\int_{\mathbb{R}^n_+}\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{(|x-y|^2+4x_ny_n)^{\frac{n-2}{2}}}\right] u^{q}(y) dy\nonumber\\
\geq& C\int_{B_1(2e_n)}\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{|x^*-y|^{n-2}}\right] dy.
\end{align}
\begin{align}
u(x)=&c_n\int_{\mathbb{R}^n_+}\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{(|x-y|^2+4x_ny_n)^{\frac{n-2}{2}}}\right] u^{q}(y) dy\nonumber\\
\geq& C\int_{B_1(2e_n)}\left[\frac{1}{|x-y|^{n-2}}-\frac{1}{|x^*-y|^{n-2}}\right] dy.
\end{align} Applying the mean value theorem to (3.8), we have for ![]() $|x| \lt 1$,
$|x| \lt 1$,
Then, for ![]() $|x|$ large,
$|x|$ large,
 \begin{equation*}
\bar{u}(x)=\frac{1}{|x|^{n-2}}u\left(\frac{x}{|x|^2}\right)\geq C\frac{x_n}{|x|^{n}}
\end{equation*}
\begin{equation*}
\bar{u}(x)=\frac{1}{|x|^{n-2}}u\left(\frac{x}{|x|^2}\right)\geq C\frac{x_n}{|x|^{n}}
\end{equation*}and
 \begin{equation*}0 \lt -c(x) \lt \frac{Cx_n^{p-1}}{|x|^{\tau+(p-1)n}}=\frac{Cx_n^{p-1}}{|x|^{n+2-p(n-2)+(p-1)n}}=\frac{Cx_n^{p-1}}{|x|^{2(p+1)}},\end{equation*}
\begin{equation*}0 \lt -c(x) \lt \frac{Cx_n^{p-1}}{|x|^{\tau+(p-1)n}}=\frac{Cx_n^{p-1}}{|x|^{n+2-p(n-2)+(p-1)n}}=\frac{Cx_n^{p-1}}{|x|^{2(p+1)}},\end{equation*}Lemma 3.2. (Decay at Infinity)
If w solves
 \begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta w+c(x)w\geq 0,~~\text{in}~ B_R^c, \\
w\geq 0,~~\text{on}~\partial B_R^c,
\end{array}
\right.
\end{equation*}
\begin{equation*}\nonumber
\left\{
\begin{array}{ll}
-\Delta w+c(x)w\geq 0,~~\text{in}~ B_R^c, \\
w\geq 0,~~\text{on}~\partial B_R^c,
\end{array}
\right.
\end{equation*} then ![]() $w\geq 0$ in
$w\geq 0$ in ![]() $B_R^c$.
$B_R^c$.
Proof. In order to get ‘Decay at infinity’ by proposition 2.3 (Comparison Principle), based on the low bound of c(x) (3.7), we construct a new comparison function. Let
 \begin{equation*}\tilde{w}_\lambda(x)=\tilde{w}(x)=\frac{w(x)}{\phi},\end{equation*}
\begin{equation*}\tilde{w}_\lambda(x)=\tilde{w}(x)=\frac{w(x)}{\phi},\end{equation*}where
 \begin{equation}
\phi(x)=x_n^r+\frac{1}{|x|^{q}},~\text{with}~0 \lt r \lt 1~\text{and}~0 \lt q \lt n-2.
\end{equation}
\begin{equation}
\phi(x)=x_n^r+\frac{1}{|x|^{q}},~\text{with}~0 \lt r \lt 1~\text{and}~0 \lt q \lt n-2.
\end{equation} For ![]() $|x| \gt R$, by calculation and using
$|x| \gt R$, by calculation and using ![]() $|x|\geq x_n \gt 0$,
$|x|\geq x_n \gt 0$,
 \begin{align}
-\Delta\phi(x)&=-\Delta (x_n^r)-\Delta \left(\frac{1}{|x|^{q}}\right)=\frac{r(1-r)}{x_n^{2-r}}+\frac{q(n-2-q)}{|x|^{2+q}}
\end{align}
\begin{align}
-\Delta\phi(x)&=-\Delta (x_n^r)-\Delta \left(\frac{1}{|x|^{q}}\right)=\frac{r(1-r)}{x_n^{2-r}}+\frac{q(n-2-q)}{|x|^{2+q}}
\end{align} \begin{align*}
\nonumber
&\geq \frac{r(1-r)}{x_n^{2-r}}\hspace{135pt}
\end{align*}
\begin{align*}
\nonumber
&\geq \frac{r(1-r)}{x_n^{2-r}}\hspace{135pt}
\end{align*} \begin{align*}
\nonumber
&\;\geq C\frac{1}{|x|^{2(p+1)}}\frac{1}{x_n^{1-p-r}}+C\frac{1}{|x|^{2(p+1)+q}}\frac{1}{x_n^{1-p}}
\end{align*}
\begin{align*}
\nonumber
&\;\geq C\frac{1}{|x|^{2(p+1)}}\frac{1}{x_n^{1-p-r}}+C\frac{1}{|x|^{2(p+1)+q}}\frac{1}{x_n^{1-p}}
\end{align*} \begin{align*}
\nonumber
&=C\frac{1}{|x|^{2(p+1)}}\frac{1}{x_n^{1-p}}\phi(x).\hspace{80pt}
\end{align*}
\begin{align*}
\nonumber
&=C\frac{1}{|x|^{2(p+1)}}\frac{1}{x_n^{1-p}}\phi(x).\hspace{80pt}
\end{align*}  $w(x)=O(\frac{1}{|x|^{n-2}})$ ensure that
$w(x)=O(\frac{1}{|x|^{n-2}})$ ensure that
 \begin{equation}
\lim\limits_{|x|\to\infty}\frac{w(x)}{\phi}=\lim\limits_{|x|\to\infty}w(x)\frac{|x|^q}{x_n^r|x|^q+1} =0.
\end{equation}
\begin{equation}
\lim\limits_{|x|\to\infty}\frac{w(x)}{\phi}=\lim\limits_{|x|\to\infty}w(x)\frac{|x|^q}{x_n^r|x|^q+1} =0.
\end{equation}Then, by proposition 2.3 (Comparison Principle), we get the conclusion.
Remark 3.3. If we choose ![]() $\phi(x)=x_n^r$, although (3.11) also holds,
$\phi(x)=x_n^r$, although (3.11) also holds,  $\lim\limits_{|x|\to\infty}\frac{w(x)}{\phi} =0$ is false. Here,
$\lim\limits_{|x|\to\infty}\frac{w(x)}{\phi} =0$ is false. Here,  $\lim\limits_{|x|\to\infty}\frac{w(x)}{\phi} =0$ ensure that
$\lim\limits_{|x|\to\infty}\frac{w(x)}{\phi} =0$ ensure that ![]() $\tilde{w}$ can attain its minimum, and thus, proposition 2.3 (Comparison Principle) works.
$\tilde{w}$ can attain its minimum, and thus, proposition 2.3 (Comparison Principle) works.
Lemma 3.4. For ![]() $0 \lt p\leq 1$, assume that
$0 \lt p\leq 1$, assume that  $u\in C^{2}(\mathbb{R}^n_+) \cap C(\overline{\mathbb{R}^n_+})$ is a solution of (P). Then, u(x) only depends on xn variable, i.e.,
$u\in C^{2}(\mathbb{R}^n_+) \cap C(\overline{\mathbb{R}^n_+})$ is a solution of (P). Then, u(x) only depends on xn variable, i.e., ![]() $u(x)=u(x_n)$.
$u(x)=u(x_n)$.
Proof. We employ the method of moving planes along any direction in ![]() $\mathbb{R}^{n-1}$ called the x 1 direction. Next, we will move the plane Tλ along the x 1 direction until λ = 0 to show that the positive solution is axially symmetric about the
$\mathbb{R}^{n-1}$ called the x 1 direction. Next, we will move the plane Tλ along the x 1 direction until λ = 0 to show that the positive solution is axially symmetric about the ![]() $x_n$-axis. We will go through the following two steps.
$x_n$-axis. We will go through the following two steps.
Step 1. We start from ![]() $-\infty$ to the right. In this step, we want to show that, for λ sufficiently negative,
$-\infty$ to the right. In this step, we want to show that, for λ sufficiently negative,
Otherwise, there exists some convergent sequence ![]() $\{x^k\}^\infty_{k=1}\subset \Sigma_\lambda$ such that
$\{x^k\}^\infty_{k=1}\subset \Sigma_\lambda$ such that
 \begin{equation}
\tilde{w}_\lambda(x^k)\to \inf\limits_{\Sigma_\lambda} \tilde{w}_\lambda(x) \lt 0,\quad
\text{as}~ k\to\infty.
\end{equation}
\begin{equation}
\tilde{w}_\lambda(x^k)\to \inf\limits_{\Sigma_\lambda} \tilde{w}_\lambda(x) \lt 0,\quad
\text{as}~ k\to\infty.
\end{equation}Note that
Thus, xk will not converge to the singular point ![]() $0^\lambda\in \Sigma_\lambda$. Thus, combining (3.1) implies that
$0^\lambda\in \Sigma_\lambda$. Thus, combining (3.1) implies that
Then, by the continuity of wλ, we obtain that
 \begin{equation}
\tilde{w}_\lambda(\hat{x}) = \inf\limits_{\Sigma_\lambda} \tilde{w}_\lambda(x) \lt 0.
\end{equation}
\begin{equation}
\tilde{w}_\lambda(\hat{x}) = \inf\limits_{\Sigma_\lambda} \tilde{w}_\lambda(x) \lt 0.
\end{equation}Therefore, ‘Decay at infinity’ implies that there exist R > 0 independent of λ such that
This is impossible since ![]() $\hat{x}\in\Sigma_\lambda$ and λ is sufficiently negative. Thus, (3.13) holds.
$\hat{x}\in\Sigma_\lambda$ and λ is sufficiently negative. Thus, (3.13) holds.
Step 2. Now, we move the plane Tλ towards the right, i.e., increasing the value of λ as long as the inequality (3.13) holds. Define
In the step, we will show that
Suppose ![]() $\lambda_0 \lt 0$, by the strong maximum principle (proposition 2.1), we either have
$\lambda_0 \lt 0$, by the strong maximum principle (proposition 2.1), we either have ![]() $w_{\lambda_0} \equiv 0$ or
$w_{\lambda_0} \equiv 0$ or
We can derive that the plane ![]() $T_{\lambda_0}$ can be moved further to the right. To be more rigorous, there exists some small
$T_{\lambda_0}$ can be moved further to the right. To be more rigorous, there exists some small ![]() $\epsilon_0 \gt 0$, such that, for
$\epsilon_0 \gt 0$, such that, for ![]() $\epsilon\in (0, \epsilon_0)$,
$\epsilon\in (0, \epsilon_0)$,
We delay proving (3.19). This inequality (3.19) contradicts with the definition of λ 0. Hence, (3.17) is valid.
Now, we prove (3.19). Suppose that (3.19) is violated for any ϵ > 0. Then, there exists a sequence of numbers ϵi tending to 0, and for each i, the corresponding negative minimum xi of ![]() $w_{\lambda_0+\epsilon_i}$. Let
$w_{\lambda_0+\epsilon_i}$. Let
 \begin{equation*}\tilde{w}_\lambda(x)=\frac{w_\lambda(x)}{\phi},\end{equation*}
\begin{equation*}\tilde{w}_\lambda(x)=\frac{w_\lambda(x)}{\phi},\end{equation*} where ![]() $\phi(x)$ defined in (3.10). By straight calculation,
$\phi(x)$ defined in (3.10). By straight calculation,
 \begin{equation}
-\Delta \tilde{w}_\lambda(x)=2\nabla \tilde{w}_\lambda\cdot\frac{\nabla\phi}{\phi}+\left(-\Delta w_\lambda(x)+\frac{\Delta\phi}{\phi}w_\lambda\right)\frac{1}{\phi}.
\end{equation}
\begin{equation}
-\Delta \tilde{w}_\lambda(x)=2\nabla \tilde{w}_\lambda\cdot\frac{\nabla\phi}{\phi}+\left(-\Delta w_\lambda(x)+\frac{\Delta\phi}{\phi}w_\lambda\right)\frac{1}{\phi}.
\end{equation} Notice that for any ![]() $\lambda\in\mathbb{R}$, the function
$\lambda\in\mathbb{R}$, the function ![]() $\tilde{w}_\lambda(x)$ tends to 0 as
$\tilde{w}_\lambda(x)$ tends to 0 as ![]() $|x|\to\infty$ since
$|x|\to\infty$ since  $\bar{u} \in O(\frac{1}{|x|^{n-2}})$. It follows that the function
$\bar{u} \in O(\frac{1}{|x|^{n-2}})$. It follows that the function ![]() $\tilde{w}_{\lambda_0+\epsilon_i}$ attains its negative minimum at some point
$\tilde{w}_{\lambda_0+\epsilon_i}$ attains its negative minimum at some point  $x^i \in \Sigma_{\lambda_0+\epsilon_i}$ for each
$x^i \in \Sigma_{\lambda_0+\epsilon_i}$ for each ![]() $i\in\mathbb{N}$. By Step 1, there exists R > 0 (independent of λ) such that
$i\in\mathbb{N}$. By Step 1, there exists R > 0 (independent of λ) such that
Then, there is a subsequence of ![]() $\{x^i \}$ (still denoted by
$\{x^i \}$ (still denoted by ![]() $\{x^i \}$), which converges to some point
$\{x^i \}$), which converges to some point ![]() $x^0\in\mathbb{R}^n_+$. Now, we have
$x^0\in\mathbb{R}^n_+$. Now, we have
 \begin{equation*}0 \leq \tilde{w}_{\lambda_0}(x^0) = \lim\limits_{i\to\infty}\tilde{w}_{\lambda_0+\epsilon_i}(x^i)\leq 0,~~
\nabla \tilde{w}_{\lambda_0}(x^0) = \lim\limits_{i\to\infty} \nabla \tilde{w}_{\lambda_0+\epsilon_i}(x^i) = 0.\end{equation*}
\begin{equation*}0 \leq \tilde{w}_{\lambda_0}(x^0) = \lim\limits_{i\to\infty}\tilde{w}_{\lambda_0+\epsilon_i}(x^i)\leq 0,~~
\nabla \tilde{w}_{\lambda_0}(x^0) = \lim\limits_{i\to\infty} \nabla \tilde{w}_{\lambda_0+\epsilon_i}(x^i) = 0.\end{equation*} That is,  $\tilde{w}_{\lambda_0}(x^0) = 0$ and
$\tilde{w}_{\lambda_0}(x^0) = 0$ and  $\nabla\tilde{w}_{\lambda_0}(x^0) = 0$. Now, we compute
$\nabla\tilde{w}_{\lambda_0}(x^0) = 0$. Now, we compute
 \begin{equation*}w_{\lambda_0}(x^0)=\tilde{w}_{\lambda_0}(x^0)\phi(x^0)=0,~~\nabla w_{\lambda_0}(x^0)=\phi(x^0)\nabla \tilde{w}_{\lambda_0}(x^0)+\tilde{w}_{\lambda_0}(x^0)\nabla\phi(x^0)=0.\end{equation*}
\begin{equation*}w_{\lambda_0}(x^0)=\tilde{w}_{\lambda_0}(x^0)\phi(x^0)=0,~~\nabla w_{\lambda_0}(x^0)=\phi(x^0)\nabla \tilde{w}_{\lambda_0}(x^0)+\tilde{w}_{\lambda_0}(x^0)\nabla\phi(x^0)=0.\end{equation*} Recalling (3.18), we see that  $x^0 \in \partial\Sigma_{\lambda_0}$. However, by Hopf’s Lemma (proposition 2.2), we have the outward normal derivative
$x^0 \in \partial\Sigma_{\lambda_0}$. However, by Hopf’s Lemma (proposition 2.2), we have the outward normal derivative  $\frac{\partial w_{\lambda_0}}{\partial\nu}(x^o) \lt 0$, which yields a contradiction. Thus, (3.19) holds.
$\frac{\partial w_{\lambda_0}}{\partial\nu}(x^o) \lt 0$, which yields a contradiction. Thus, (3.19) holds.
We have already pointed out earlier that (3.19) implies (3.17), then by (3.17)
Similarly, we can move the plane from near ![]() $+\infty$ to the left limiting position, and we have
$+\infty$ to the left limiting position, and we have
Combining (3.21) with (3.22), we can conclude
Since the direction of the ![]() $x_1$-axis is arbitrary, we derive that the solution
$x_1$-axis is arbitrary, we derive that the solution ![]() $\bar{u}(x)$ of (3.2) is axially symmetric about the
$\bar{u}(x)$ of (3.2) is axially symmetric about the ![]() $x_n$-axis.
$x_n$-axis.
Now, for any ![]() $x^0\in\partial\mathbb{R}^n_+$, let
$x^0\in\partial\mathbb{R}^n_+$, let ![]() $\bar{u}$ be the Kelvin transformation of u centred at x 0,
$\bar{u}$ be the Kelvin transformation of u centred at x 0,
 \begin{equation*}\bar{u}_{x^0}(x) = \frac{1}{|x-x^0|^{n-2}}u\left(\frac{x-x^0}{|x-x^0|^2}+x^0\right),~~\forall x \in \mathbb{R}^n\setminus\{x^0\}.\end{equation*}
\begin{equation*}\bar{u}_{x^0}(x) = \frac{1}{|x-x^0|^{n-2}}u\left(\frac{x-x^0}{|x-x^0|^2}+x^0\right),~~\forall x \in \mathbb{R}^n\setminus\{x^0\}.\end{equation*} Using an entirely similar argument, one can verify that ![]() $\bar{u}$ is axially symmetric about the line parallel to the xn axis and passing through x 0. For the arbitrariness of x 0, we can conclude that
$\bar{u}$ is axially symmetric about the line parallel to the xn axis and passing through x 0. For the arbitrariness of x 0, we can conclude that ![]() $\bar{u}$ is rotationally symmetric with respect to the line parallel to the xn axis. Choosing any two points x 1 and x 2 in
$\bar{u}$ is rotationally symmetric with respect to the line parallel to the xn axis. Choosing any two points x 1 and x 2 in ![]() $\mathbb{R}^n_+$ we have
$\mathbb{R}^n_+$ we have
Let z 0 be the projection of the midpoint  $x^0 = \frac{x^1+x^2}{2}$, where
$x^0 = \frac{x^1+x^2}{2}$, where ![]() $z^0\in\partial\mathbb{R}^n_+$. By the proof of above, we know
$z^0\in\partial\mathbb{R}^n_+$. By the proof of above, we know ![]() $\bar{u}$ is axially symmetric with respect to
$\bar{u}$ is axially symmetric with respect to ![]() $\overline{x^0z^0}$. Setting
$\overline{x^0z^0}$. Setting
 \begin{equation*}y^1 =\frac{x^1 - z^0}{|x^1 - z^0|^2} + z^0,~~
y^2 =\frac{x^2 - z^0}{|x^2 - z^0|^2} + z^0,\end{equation*}
\begin{equation*}y^1 =\frac{x^1 - z^0}{|x^1 - z^0|^2} + z^0,~~
y^2 =\frac{x^2 - z^0}{|x^2 - z^0|^2} + z^0,\end{equation*} it is easy to see ![]() $\bar{u}(y^1) = \bar{u}(y^2)$. Hence
$\bar{u}(y^1) = \bar{u}(y^2)$. Hence ![]() $u(x^1) = u(x^2)$. This implies that the positive solution of (P) only depends on xn variable, i.e.,
$u(x^1) = u(x^2)$. This implies that the positive solution of (P) only depends on xn variable, i.e., ![]() $u(x) = u(x_n)$. This completes the proof of lemma 3.4.
$u(x) = u(x_n)$. This completes the proof of lemma 3.4.
Proposition 3.5. If ![]() $u=u(x_n) \gt 0$, then
$u=u(x_n) \gt 0$, then
 \begin{equation*}u(x_n)=\int_{\mathbb{R}^n_+}G(x,y) u^{p}(y) dy=+\infty.\end{equation*}
\begin{equation*}u(x_n)=\int_{\mathbb{R}^n_+}G(x,y) u^{p}(y) dy=+\infty.\end{equation*}Proof. Let R > 0 be any fixed number. For ![]() $x_n \gt R$, by (2.9), we have
$x_n \gt R$, by (2.9), we have
 \begin{align*}
+\infty \gt u(x_n)\geq &\,C\int_0^{R} u^{q}(y_n)\text{d}y_n\int_{\mathbb{R}^{n-1}}G(x,y)dy' \\
\geq &\,C \int_0^{R} u^{q}(y_n)\left(|x_n+y_n|-|x_n-y_n|\right)dy_n \\
= &\,2C\int_0^{R} u^{q}(y_n)2y_ndy_n.
\end{align*}
\begin{align*}
+\infty \gt u(x_n)\geq &\,C\int_0^{R} u^{q}(y_n)\text{d}y_n\int_{\mathbb{R}^{n-1}}G(x,y)dy' \\
\geq &\,C \int_0^{R} u^{q}(y_n)\left(|x_n+y_n|-|x_n-y_n|\right)dy_n \\
= &\,2C\int_0^{R} u^{q}(y_n)2y_ndy_n.
\end{align*}This implies that
For ![]() $x_n\in(0,R)$, using (2.9) again, we obtain
$x_n\in(0,R)$, using (2.9) again, we obtain
 \begin{align}
+\infty \gt u(x_n)\geq &\,C\int_R^\infty u^{q}(y_n)dy_n\int_{\mathbb{R}^{n-1}}G(x,y)dy' \nonumber\\
\geq &\,C \int_R^\infty u^{q}(y_n)\left(|x_n+y_n|-|y_n-x_n|\right)dy_n\\
\geq &\,2Cx_n\int_R^\infty u^{q}(y_n) dy_n.\nonumber
\end{align}
\begin{align}
+\infty \gt u(x_n)\geq &\,C\int_R^\infty u^{q}(y_n)dy_n\int_{\mathbb{R}^{n-1}}G(x,y)dy' \nonumber\\
\geq &\,C \int_R^\infty u^{q}(y_n)\left(|x_n+y_n|-|y_n-x_n|\right)dy_n\\
\geq &\,2Cx_n\int_R^\infty u^{q}(y_n) dy_n.\nonumber
\end{align} Then by (3.24), for ![]() $x_n\in(0,R)$ we get
$x_n\in(0,R)$ we get
 \begin{equation}
+\infty \gt u(x_n)\geq Cx_n\int_R^\infty C_1^qdy_n= +\infty.
\end{equation}
\begin{equation}
+\infty \gt u(x_n)\geq Cx_n\int_R^\infty C_1^qdy_n= +\infty.
\end{equation}Proof of Theorem 1.1
Combining lemma 3.4, proposition 2.5, and proposition 3.5, we complete the proof of theorem 1.1.
Acknowledgements
The author would like to thank Professor Congming Li for many precious suggestions.
This work was partially supported by National Natural Science Foundation of China (NSFC) (11901532)and Shanghai Jiao Tong University Scientific and Technological Innovation Funds.