Published online by Cambridge University Press: 04 April 2014
The changes in a turbulent channel flow subjected to sinusoidal oscillations of wall flush-mounted rigid discs are studied by means of direct numerical simulations (DNS). The Reynolds number is
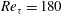 ${Re}_{\tau }=180$
, based on the friction velocity of the stationary-wall case and the half-channel height. The primary effect of the wall forcing is the sustained reduction of wall-shear stress, which reaches a maximum of 20 %. A parametric study on the disc diameter, maximum tip velocity, and oscillation period is presented, with the aim of identifying the optimal parameters which guarantee maximum drag reduction and maximum net energy saving, the latter computed by taking into account the power spent to actuate the discs. This may be positive and reaches 6 %. The Rosenblat viscous pump flow, namely the laminar flow induced by sinusoidal in-plane oscillations of an infinite disc beneath a quiescent fluid, is used to predict accurately the power spent for disc motion in the fully developed turbulent channel flow case and to estimate localized and transient regions over the disc surface subjected to the turbulent regenerative braking effect, for which the wall turbulence exerts work on the discs. The Fukagata–Iwamoto–Kasagi identity is employed effectively to show that the wall-friction reduction is due to two distinguished effects. One effect is linked to the direct shearing action of the near-wall oscillating-disc boundary layer on the wall turbulence, which causes the attenuation of the turbulent Reynolds stresses. The other effect is due to the additional disc-flow Reynolds stresses produced by the streamwise-elongated structures which form between discs and modulate slowly in time. The contribution to drag reduction due to turbulent Reynolds stress attenuation depends on the penetration thickness of the disc-flow boundary layer, while the contribution due to the elongated structures scales linearly with a simple function of the maximum tip velocity and oscillation period for the largest disc diameter tested, a result suggested by the Rosenblat flow solution. A brief discussion on the future applicability of the oscillating-disc technique is also presented.
${Re}_{\tau }=180$
, based on the friction velocity of the stationary-wall case and the half-channel height. The primary effect of the wall forcing is the sustained reduction of wall-shear stress, which reaches a maximum of 20 %. A parametric study on the disc diameter, maximum tip velocity, and oscillation period is presented, with the aim of identifying the optimal parameters which guarantee maximum drag reduction and maximum net energy saving, the latter computed by taking into account the power spent to actuate the discs. This may be positive and reaches 6 %. The Rosenblat viscous pump flow, namely the laminar flow induced by sinusoidal in-plane oscillations of an infinite disc beneath a quiescent fluid, is used to predict accurately the power spent for disc motion in the fully developed turbulent channel flow case and to estimate localized and transient regions over the disc surface subjected to the turbulent regenerative braking effect, for which the wall turbulence exerts work on the discs. The Fukagata–Iwamoto–Kasagi identity is employed effectively to show that the wall-friction reduction is due to two distinguished effects. One effect is linked to the direct shearing action of the near-wall oscillating-disc boundary layer on the wall turbulence, which causes the attenuation of the turbulent Reynolds stresses. The other effect is due to the additional disc-flow Reynolds stresses produced by the streamwise-elongated structures which form between discs and modulate slowly in time. The contribution to drag reduction due to turbulent Reynolds stress attenuation depends on the penetration thickness of the disc-flow boundary layer, while the contribution due to the elongated structures scales linearly with a simple function of the maximum tip velocity and oscillation period for the largest disc diameter tested, a result suggested by the Rosenblat flow solution. A brief discussion on the future applicability of the oscillating-disc technique is also presented.
Please note a has been issued for this article.