Despite the fact that in 1988 respected geneticist C. C. Li demonstrated that Hardy-Weinberg proportions can be maintained by non-random mating, and that the subject was worth further investigation, the genetics community maintains the pretence of ‘random mating’. This paper illustrates how a sample generated by non-random mating frequently can be perceived as coming from a population practising random mating.
The title of this article has been borrowed from the song in the musical Man of La Mancha. It expresses the notion of an unattainable ideal. Perfect random mating and Hardy-Weinberg proportions are unattainable in practice. As an abstraction it is not obvious how to define random mating for a finite population. This does not exclude Hardy’s law from practical application. Weinberg (Reference Weinberg1908) used the formulae to study the propensity to produce twins in a segment of the German population. The textbook presentation of the Hardy-Weinberg principle should be rewritten to include pseudo- and quasi-random mating.
Smith (Reference Smith1969, p. 200) expresses the traditional view of the Hardy-Weinberg law as follows: ‘Now married couples do not come together on a basis of their MN blood-groups, whatever other reasons they may have. So we may well expect that, as far as blood-groups are concerned, mating will be at random (“panmixia”)’. Following this assumption, Smith produces the frequency of couple MN, MM chosen at random from the population as P MN X P MM. Smith then finds the frequencies of a child drawn at random from the population to be the Hardy-Weinberg proportions.
Stark (Reference Stark2023) presents a concise genetics model that produces Hardy-Weinberg frequencies for an autosomal locus with two alleles, in one generation, starting from arbitrary frequencies. This model provides some justification for the fact that approximate Hardy-Weinberg proportions are often observed. In this model mating proportions are controlled by a single parameter h which allows flexibility. Setting h = 0 defines ‘random mating’. The object of this paper is to illustrate, by simulation, that it is difficult to distinguish random from non-random mating in samples of mating proportions generated by setting a non-zero value of h.
It appears that the details of Li’s paper are not well known. For this reason a brief outline is given in the next section. This is followed by the model of quasi-random mating, the simulation and a section that attempts to create an impression of how the genetics community views the Hardy-Weinberg law.
Pseudo-Random Mating
The Wikipedia version of the Hardy-Weinberg principle has obscured the basic simplicity of G. H. Hardy’s (Reference Hardy1908) original law. Also, it has diverted attention from the observation by C. C. Li (Reference Li1988) that Hardy-Weinberg proportions can be maintained by non-random mating which Li called ‘pseudo-random mating’. In Li’s notation random mating is defined by
![]() ${f_{ij}} = {f_i}{f_j}$
and non-random mating by
${f_{ij}} = {f_i}{f_j}$
and non-random mating by
![]() ${f_{ij}} = {f_i}{f_j} + {d_{ij}}$
, where
${f_{ij}} = {f_i}{f_j} + {d_{ij}}$
, where
![]() ${d_{ij}}$
is the deviation from random-mating frequency. Li (Reference Li1988) says: ‘The properties of panmixia are well known’ (p. 731).
${d_{ij}}$
is the deviation from random-mating frequency. Li (Reference Li1988) says: ‘The properties of panmixia are well known’ (p. 731).
C. C. Li (Reference Li1988) defined pseudo-random mating by means of the model shown in Table 1, with minimal explanation, except by pointing out that the mating proportions given can be shown to produce offspring in the same proportions as the parents. He says that Table 1 has the ‘pseudo-random mating property’ (p. 732). Table 1 does not have equal reciprocal mating frequencies, unlike Hardy’s model. Later, Li reaches the symmetrical model characterized by the condition c 33 = 4c 12, as dealt with in the next section. This condition reproduces any genotypic distribution.
Table 1. Algebraic mating proportions reproducing Hardy-Weinberg offspring devised by C. C. Li (Reference Li1988). The order of genotypes has been rearranged.

The mating proportions given in Table 1 follow Li’s prescription given in the first paragraph of the introduction above. The quantity x can be varied providing it conforms to the constraints of the table. Li considers other aspects of pseudo-random mating that do not change the main property of Table 1, which is that the offspring have the same genotypic proportions as the parents. The terms involving x cancel each other as can be shown by applying Mendel’s rule to the mating proportions. The other terms follow Hardy’s rule.
Other sets of coefficients for x can be found as explored by Li. The details of the logic involved may be the reason why the genetics community has not embraced Li’s findings. The other aspects of pseudo-random mating considered by Li are parental correlation, gametic independence and sib-sib correlation. Following Wright (Reference Wright1921), Li gives values 0, 1 and 2 to genotypes. Li makes an ambiguous comment: ‘Since there are an infinite number of possible pseudo-random mating patterns, we cannot be sure that none of them exists in nature’ (p. 733). Li concludes: ‘When we observe reasonable agreement with random mating expectations from a sample, we really could not be sure what the mating pattern might be in the population’ (p. 737).
Quasi-Random Mating
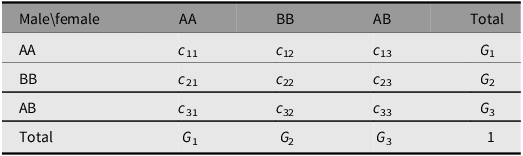
Consider an autosomal locus with two alleles A and B and genotypes AA, BB and AB numbered 1, 2 and 3. Mating pairs are formed in the current generation to produce offspring in the next. The proportions of the mating pairs are given symbolically in Table 2. The elements c ij are non-negative and symmetrical in value (c ij = c ji) and sum to 1.
Table 2. Symbolic mating proportions reproducing offspring
Suppose that the genotypic proportions are
F measures departure from Hardy-Weinberg form and the gene frequencies are
![]() $q = (2{G_1} + {G_3})/2;p = (2{G_2} + {G_3})/2 = 1 - q$
.
$q = (2{G_1} + {G_3})/2;p = (2{G_2} + {G_3})/2 = 1 - q$
.
The mating frequencies are
where
![]() ${e_1} = p(F - 1)/(q + Fp);{e_2} = q(F - 1)/(p + Fq);{e_3} = 1;$
and
${e_1} = p(F - 1)/(q + Fp);{e_2} = q(F - 1)/(p + Fq);{e_3} = 1;$
and
![]() $v = pq(1 - {F^2})/((q + Fp)(p + Fq)).$
For fixed q, v increases monotonically from zero to 1 as F decreases from 1 to zero.
$v = pq(1 - {F^2})/((q + Fp)(p + Fq)).$
For fixed q, v increases monotonically from zero to 1 as F decreases from 1 to zero.
The gene frequencies are not changed through the action of (1). Subject to constraints h can be chosen over a wide range allowing uncountable possibilities for varying the mating regime but still producing, in one generation, offspring distributed according to the Hardy-Weinberg formulae:
This can be verified by calculating the offspring frequencies by applying Mendel’s rule to (1):
A numerical example illustrating model (1) is given in Stark (Reference Stark2023).
The Simulation
The object of this note is to explore the question of whether a standard statistical test is likely to be able to identify a departure from random mating in a hypothetical collection of genetic data.
The performance of an estimator of h assuming that couples are formed following model (1) is studied by simulation. This is done by drawing random samples of couples and using the observed numbers of pairs of genotypes to calculate q and F from each sample and, using these values, to make a maximum likelihood estimate of h. It is assumed that the only information available is the number of pairs of each type and so estimates of q and F must first be made from these counts.
Denoting the random number of pairs of genotypes i and j by n ij, the likelihood of the sample is proportional to
Heuristic estimates of q and F are formed:
using the notation given above the estimates from each sample are
 $$\begin{gathered}q = (4{n_{11}} + 2{n_{12}} + 3{n_{13}} + 2{n_{21}} + {n_{23}} + 3{n_{31}} + {n_{32}} \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!+ 2{n_{33}})/(4N), \\ \end{gathered}$$
$$\begin{gathered}q = (4{n_{11}} + 2{n_{12}} + 3{n_{13}} + 2{n_{21}} + {n_{23}} + 3{n_{31}} + {n_{32}} \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!+ 2{n_{33}})/(4N), \\ \end{gathered}$$
and
where N is the number of couples in the sample. Using these estimates of q and F, taking the logarithm of expression (3), for each sample the maximum likelihood estimate of h is obtained. This is done by taking a fine grid of potential values of h and choosing the one of greatest likelihood.
Figure 1 illustrates a typical outcome, in this case by generating couples taking h = 1/200. The mean of the data displayed in the histogram is 0.005442 and the standard error is 0.0201. In this case 2500 couples were generated in each sample and 1000 estimates of h were made. Although this is of lesser interest the starting value of q = ¼ and of F = 1/3. The important point to note is that there is no clear distinction between h = 0 and values near this.

Figure 1. Histogram of estimates of h based on samples generated from a population value h = 1/200.
As Figure 1 illustrates, there is no reason why a test of goodness of fit might not contradict the Hardy-Weinberg expectation but may be underpinned by non-random mating.
Figure 2 gives an indication of the dependence of the estimate of h on the size of the sample of pairs of mating couples. The number of couples is plotted on the horizontal axis and the standard error of estimate on the vertical.

Figure 2. Simulated standard errors of estimates of h as a function of the size of samples of the number of couples N.
Grassroots
Wright (Reference Wright1959, p. 107) indicates the place of the Hardy-Weinberg principle as follows:
The theoretical genetics of populations may be considered to have begun with [Karl] Pearson’s demonstration that the 1:2:1 Mendelian ratio tends to maintain itself indefinitely in a large random-breeding population derived from F2 of a cross. A few years later Hardy and Weinberg independently pointed out that any array of gene frequencies at a locus (
![]() $\sum {{q_{{I_i}}}} {A_{{I_i}}}$
, where
$\sum {{q_{{I_i}}}} {A_{{I_i}}}$
, where
![]() ${A_{{I_i}}}$
is a particular allele at locus
${A_{{I_i}}}$
is a particular allele at locus
![]() ${A_I}$
and
${A_I}$
and
![]() ${q_{_{{I_i}}}}$
is its proportional frequency) tends to remain unchanged in a large self-contained population in the absence of disturbing factors such as mutation and selection, and thus that the frequency of the zygotes resulting from random mating becomes stable immediately after attainment of equality of gene frequencies in the sexes in the array
${q_{_{{I_i}}}}$
is its proportional frequency) tends to remain unchanged in a large self-contained population in the absence of disturbing factors such as mutation and selection, and thus that the frequency of the zygotes resulting from random mating becomes stable immediately after attainment of equality of gene frequencies in the sexes in the array
![]() ${\left( {\sum {{q_{{I_i}}}} {A_{{I_i}}}} \right)^2}$
for one locus. If mating is not at random, the zygotic array, in the absence of other disturbing factors, is given by
${\left( {\sum {{q_{{I_i}}}} {A_{{I_i}}}} \right)^2}$
for one locus. If mating is not at random, the zygotic array, in the absence of other disturbing factors, is given by
![]() $(1 - F){\left[ {\sum {{q_{{I_i}}}} {A_{{I_i}}}} \right]^2} + F{({q_{{I_i}}}{A_{{I_{_i}}}}{A_{{I_i}}})_{}}$
, where F is the inbreeding coefficient, defined as the correlation between uniting gametes with respect to additive effects.
$(1 - F){\left[ {\sum {{q_{{I_i}}}} {A_{{I_i}}}} \right]^2} + F{({q_{{I_i}}}{A_{{I_{_i}}}}{A_{{I_i}}})_{}}$
, where F is the inbreeding coefficient, defined as the correlation between uniting gametes with respect to additive effects.
This statement, which is typical of the genetics literature, conflates the essence of Hardy’s original deterministic abstraction with qualifications about real populations that would make them consistent with Hardy’s model. This leaves no room to accommodate Li’s pseudo-random mating or the quasi-random mating model.
Dobzhansky (Reference Dobzhansky1951) introduces the Hardy-Weinberg law by combining two strains of a sexual and cross-fertilizing organism that differ in a single gene AA and aa, that they interbreed at random, and that they are introduced in the proportions q of AA and (1−q) of aa. He asks the question, what will be the resulting Mendelizing population in the next and following generations. He says that the solution is the Hardy-Weinberg, or the binomial square, law. He adds: ‘If there is some breeding preference, such as a tendency towards inbreeding or self-fertilization, the relative frequencies of the homozygotes (AA and aa) and the heterozygotes (Aa) will be modified, but the gene frequencies, q and (1 – q), will still remain constant’ (p. 53).
Dobzhansky’s explanation is consistent with the standard textbook version of the Hardy-Weinberg law. Malécot (Reference Malécot1969) outlines population genetics theory in probabilistic terms, which permits him to switch between infinite and finite populations. ‘Panmixia’ is listed separately in the index and appears repeatedly in the book. One of the cases dealt with is described as follows: ‘The parents mate at random; the probability of finding a mate is the same for all individuals; and fecundity is the same for all couples. This is <<random mating>>, panmixia.’
Malécot (Reference Malécot1969) has a section dealing with the increase of coancestry in a finite population and gives the formulae for genotypic frequencies. He adds the footnote: ‘The above formulas are based on the assumption that there is only random inbreeding (consistent with panmixia)’ (p. 32).
With respect to variations in populations, Philip (Reference Philip1938, p. 198) writes: ‘It is possible … to decide genetically in some cases whether a population is inbred, or whether there is random mating.’ Philip’s method is to test against Pearson’s and Hardy’s law expressed as
u being the ‘ratio of the dominant gene A to the recessive gene a’.
Philip used the beetle Dermestes vulpinus, recording two characters, wing colour and pigment density. The alleles of the first character were dark (dominant) and light (recessive). The beetles were collected either as larvae, pupae, or imagines. An elaborate procedure was required to test for random mating. The analysis was based on 237 beetles. A backcross was used to separate the dark animals into homozygotes and heterozygotes. The almost perfect agreement between observed and expected frequencies was obtained by using the result of the backcross to estimate gene frequencies. Philip comments: ‘This fits well with the assumption of random mating if the relative distribution of the genes in the population is 18.7% for L and 81.3% for l)’ (p. 201). Malécot (Reference Malécot1969, p. 14) cites Philip (Reference Philip1938) for finding an example (the beetle above) of a natural population exhibiting Hardy’s law.
Haldane (Reference Haldane1938) cites Philip (Reference Philip1938) as obtaining indirect evidence concerning the mating system. Haldane’s comment, which is appropriate to Philip’s methodology is: ‘… we may find that the frequencies of the three genotypes are so close to those which would be expected from random mating that the divergences may be ascribed to chance’ (p. 213).
There is no single clear definition of ‘random mating’. It is applied to abstract settings for finite and infinite populations and real populations. Often it is assumed that no definition is needed since everybody understands what it means. In setting out his Fundamental Theorem of Natural Selection Fisher (Reference Fisher1930, p. 35) writes: ‘Since the theorem is exact for idealized populations … It will be sufficient … to consider the special case of a population mating and reproducing at random.’ Fisher does not say what this means but a definition is implicit when he gives the variance of a chance fluctuation in the gene frequency as that obtainable from the binomial distribution.
Uspenky (Reference Uspensky1937, pp. 9−11) chose Mendelian genetics to illustrate the application of probability to a branch of science. He used what he refers to as the classical definition of probability. In essence, if an event occurs in r out of n equally likely ways, its probability of occurrence is r/n. In Mendel’s case, if gametes are joined from two heterozygotes, the four possible outcomes each have probability ¼. Uspensky emphasizes the precision of this theory and contrasts it with the lack of an equally precise model to predict the sex ratio in humans. Uspensky does not consider the Hardy-Weinberg law.
Acknowledgment
I thank the reviewer for critical comments and constructive suggestions.
Financial support
None.
Competing interests
None.
Ethical standards
No experimental subjects were involved.
Publication ethics
Sources acknowledged.







