1 INTRODUCTION
The equation of state (EoS) of matter inside neutron stars has received a lot of attention over the last decades (Lattimer & Prakash Reference Lattimer and Prakash2004, Reference Lattimer and Prakash2007; Oertel et al. Reference Oertel, Hempel, Klähn and Typel2017). Besides black holes, neutron stars (usually observed as pulsars) are the most compact known objects in the universe. Their bulk features, such as mass and radius, strongly depend on the properties of matter in their interior and, hence, on the EoS.
With regards to mass determinations, the most precise measurements of masses are clustered around the Hulse–Taylor pulsar of 1.4M⊙ (Hulse & Taylor Reference Hulse and Taylor1975). However, accurate values of approximately 2 M⊙ have been determined very recently. This is the case of the PSR J1614−2230 of M = 1.97 ± 0.04M⊙ (Demorest et al. Reference Demorest, Pennucci, Ransom, Roberts and Hessels2010) and the PSR J0348+0432 of M = 2.01 ± 0.04M⊙ (Antoniadis et al. Reference Antoniadis2013).
As for radii, precise determinations do not yet exist due to the difficulties in modelling the X-ray spectra emitted by the atmosphere of a neutron star (Verbiest et al. Reference Verbiest2008; Ozel, Baym, & Guver Reference Ozel, Baym and Guver2010; Suleimanov et al. Reference Suleimanov, Poutanen, Revnivtsev and Werner2011; Lattimer & Lim Reference Lattimer and Lim2013; Steiner, Lattimer, & Brown Reference Steiner, Lattimer and Brown2013; Bogdanov Reference Bogdanov2013; Guver & Ozel Reference Guver and Ozel2013; Guillot et al. Reference Guillot, Servillat, Webb and Rutledge2013; Lattimer & Steiner Reference Lattimer and Steiner2014a; Poutanen et al. Reference Poutanen, Nattila, Kajava, Latvala, Galloway, Kuulkers and Suleimanov2014; Heinke et al. Reference Heinke2014; Guillot & Rutledge Reference Guillot and Rutledge2014; Ozel et al. Reference Ozel, Psaltis, Guver, Baym, Heinke and Guillot2016; Ozel & Psaltis Reference Ozel and Psaltis2015; Ozel & Freire Reference Ozel and Freire2016; Lattimer & Prakash Reference Lattimer and Prakash2016). Nevertheless, most of these analysis seem to favour small radii below 13 km (Fortin et al. Reference Fortin, Zdunik, Haensel and Bejger2015). High-precision X-ray space missions, such as the ongoing NICER (Neutron star Interior Composition ExploreR) (Arzoumanian et al. Reference Arzoumanian, Takahasi, den Herder and Bautz2014), will shed some light by offering simultaneous measurements of masses and radii (Watts et al. Reference Watts2016), whereas neutron-star radii are expected to be measured with a precision of 1 km by means of gravitational-wave signals coming from neutron-star mergers (Bauswein & Janka Reference Bauswein and Janka2012; Lackey & Wade Reference Lackey and Wade2015).
In view of these findings and future observations, it is opportune to analyse whether theoretical models for the EoS of dense matter can satisfy both the 2M⊙ maximum mass constraint and radii below 13 km. Moreover, these models should fulfil the saturation propertiesFootnote 1 of nuclear matter and finite nuclei (or atomic nuclei). On the one hand, in order to obtain small neutron star radii, a softening of the pressure of neutron matter, and hence of the nuclear symmetry energy, around 1–2 times saturation density n 0 (n 0 ≈ 0.16 fm−3) is required (Lattimer & Prakash Reference Lattimer and Prakash2007; Tsang et al. Reference Tsang2012; Ozel & Freire Reference Ozel and Freire2016). On the other hand, the total pressure should be stiff enough in order to sustain 2M⊙ neutron stars. Very few models can reconcile simultaneously both constraints (small radius and large masses) and, at the same time, produce a precise description of finite nuclei (Jiang, Li, & Fattoyev Reference Jiang, Li and Fattoyev2015; Horowitz & Piekarewicz Reference Horowitz and Piekarewicz2001a, Reference Horowitz and Piekarewicz2001b; Chen & Piekarewicz Reference Chen and Piekarewicz2015a; Sharma et al. Reference Sharma, Centelles, Viñas, Baldo and Burgio2015).
Furthermore, as density increases inside neutron stars, the transition from nuclear to hyperonic matter would be favoured energetically (Ambartsumyan & Saakyan Reference Ambartsumyan and Saakyan1960). Thus, the EoS softens as new degrees of freedom, hyperons, appear (Glendenning Reference Glendenning1982) leading to smaller neutron stars masses, below the 2M⊙ observations. This is known as the ‘hyperon puzzle’, whose solution requires a new mechanism to stiffen the EoS: stiffer hyperon–nucleon and/or hyperon–hyperon interactions, repulsive three-body forces with hyperons, new hadronic degrees of freedom that push the onset of appearance of hyperons to higher densities or the phase transition to quark matter below the hyperon onset [see ref. Chatterjee & Vidana (Reference Chatterjee and Vidana2016) and references herein].
In a recent paper (Tolos, Centelles, & Ramos Reference Tolos, Centelles and Ramos2017), we have obtained the EoS for the nucleonic and hyperonic inner core of neutron stars by reconciling the 2M⊙ mass observations with the recent analyses of radii below 13 km for neutron stars. Moreover, we have fulfilled the saturation properties of nuclear matter and finite nuclei (Tsang et al. Reference Tsang2012; Chen & Piekarewicz Reference Chen and Piekarewicz2014) as well as the recent constraints extracted from nuclear collective flow (Danielewicz, Lacey, & Lynch Reference Danielewicz, Lacey and Lynch2002) and kaon production (Fuchs et al. Reference Fuchs, Faessler, Zabrodin and Zheng2001; Lynch et al. Reference Lynch, Tsang, Zhang, Danielewicz, Famiano, Li and Steiner2009) in heavy-ion collisions (HICs). The study was performed in the relativistic mean-field (RMF) theory for describing both the nucleon and hyperon interactions and the EoS of the neutron star core. Two models were formulated, denoted as FSU2R (with nucleons) and FSU2H (with nucleons and hyperons), based on the nucleonic FSU2 model of Chen & Piekarewicz (Reference Chen and Piekarewicz2014).
In the present paper, we update the parameters of our two models in order to improve the behaviour of the EoS of pure neutron matter (PNM) at subsaturation densities by avoiding possible instabilities in the low-density region. We determine the properties at saturation of the modified interactions and we compare our results for the symmetry energy and the slope of the symmetry energy to recent experimental and theoretical determinations, while providing predictions for the neutron skin thickness of the 208Pb and 48Ca nuclei. Finally, we reinvestigate the mass–radius relationships for the two models, and estimate the impact on the neutron star masses, radii, and composition of the uncertainties in the hyperon–nucleon couplings.
The paper is organised as follows. In Section 2, we present the RMF model for the determination of the EoS in beta-equilibrated matter. In Section 3, we show the newly calibrated nucleonic FSU2R and hyperonic FSU2H models. Then, in Section 4, we display the results for the mass–radius relationship for neutron stars and in Section 5, we estimate the impact on the stellar properties of the uncertainties in the hyperon–nucleon couplings. We finally summarise our results in Section 6. Tables with numerical data of the EoSs are provided in the Appendix.
2 THEORETICAL FRAMEWORK
In the covariant field theory of hadronic matter, the baryons are treated as Dirac particles that interact through the exchange of mesons (Serot & Walecka Reference Serot and Walecka1986). The formalism has been in wide use over the last four decades for describing the properties of the nuclear EoS and of finite nuclei in a relativistic quantum framework. A contemporary formulation of the Lagrangian density of the theory (Serot & Walecka Reference Serot and Walecka1986, Reference Serot and Walecka1997; Glendenning Reference Glendenning2000; Chen & Piekarewicz Reference Chen and Piekarewicz2014) may be written in terms of the contributions from the baryons (b), leptons (l=e, μ), and mesons (m = σ, ω, ρ, and ϕ) as
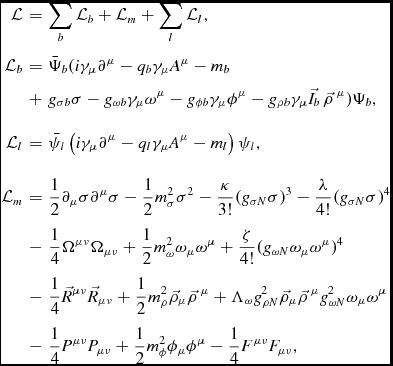 $$\begin{eqnarray}
{\cal L} &=& \sum _{b}{\cal L}_{b} + {\cal L}_{m}+ \sum _{l}{\cal L}_{l} , \nonumber \\
{\cal L}_{b}&=&\bar{\Psi }_{b}(i\gamma _{\mu }\partial ^{\mu }-q_{b}\gamma _{\mu }A^{\mu }- m_{b} \nonumber \\
&+& g_{\sigma b}\sigma -g_{\omega b}\gamma _{\mu }\omega ^{\mu }-g_{\phi b}\gamma _{\mu }\phi ^{\mu }-g_{\rho b}\gamma _{\mu }\vec{I}_b \, \vec{\rho \, }^{\mu } )\Psi _{b} , \nonumber \\
[2mm]{\cal L}_{l}&=& \bar{\psi }_{l}\left(i\gamma _{\mu }\partial ^{\mu }-q_{l}\gamma _{\mu }A^{\mu } -m_{l}\right)\psi _{l} ,\nonumber \\
[2mm]{\cal L}_{m}&=&\frac{1}{2}\partial _{\mu }\sigma \partial ^{\mu }\sigma -\frac{1}{2}m^{2}_{\sigma }\sigma ^{2} - \frac{\kappa }{3!} (g_{\sigma N}\sigma )^3 - \frac{\lambda }{4!} (g_{\sigma N}\sigma )^4 \nonumber \\
&-& \frac{1}{4}\Omega ^{\mu \nu } \Omega _{\mu \nu } +\frac{1}{2}m^{2}_{\omega }\omega _{\mu }\omega ^{\mu } + \frac{\zeta }{4!} (g_{\omega N}\omega _{\mu } \omega ^{\mu })^4 \nonumber \\
&-&\frac{1}{4} \vec{R}^{\mu \nu }\vec{R}_{\mu \nu }+\frac{1}{2}m^{2}_{\rho }\vec{\rho }_{\mu }\vec{\rho \, }^{\mu } + \Lambda _{\omega } g_{\rho N}^2 \vec{\rho }_{\mu }\vec{\rho \,}^{\mu } g_{\omega N}^2 \omega _{\mu } \omega ^{\mu } \nonumber \\
&-&\frac{1}{4} P^{\mu \nu }P_{\mu \nu }+\frac{1}{2}m^{2}_{\phi }\phi _{\mu }\phi ^{\mu } -\frac{1}{4} F^{\mu \nu }F_{\mu \nu } ,
\end{eqnarray}$$
$$\begin{eqnarray}
{\cal L} &=& \sum _{b}{\cal L}_{b} + {\cal L}_{m}+ \sum _{l}{\cal L}_{l} , \nonumber \\
{\cal L}_{b}&=&\bar{\Psi }_{b}(i\gamma _{\mu }\partial ^{\mu }-q_{b}\gamma _{\mu }A^{\mu }- m_{b} \nonumber \\
&+& g_{\sigma b}\sigma -g_{\omega b}\gamma _{\mu }\omega ^{\mu }-g_{\phi b}\gamma _{\mu }\phi ^{\mu }-g_{\rho b}\gamma _{\mu }\vec{I}_b \, \vec{\rho \, }^{\mu } )\Psi _{b} , \nonumber \\
[2mm]{\cal L}_{l}&=& \bar{\psi }_{l}\left(i\gamma _{\mu }\partial ^{\mu }-q_{l}\gamma _{\mu }A^{\mu } -m_{l}\right)\psi _{l} ,\nonumber \\
[2mm]{\cal L}_{m}&=&\frac{1}{2}\partial _{\mu }\sigma \partial ^{\mu }\sigma -\frac{1}{2}m^{2}_{\sigma }\sigma ^{2} - \frac{\kappa }{3!} (g_{\sigma N}\sigma )^3 - \frac{\lambda }{4!} (g_{\sigma N}\sigma )^4 \nonumber \\
&-& \frac{1}{4}\Omega ^{\mu \nu } \Omega _{\mu \nu } +\frac{1}{2}m^{2}_{\omega }\omega _{\mu }\omega ^{\mu } + \frac{\zeta }{4!} (g_{\omega N}\omega _{\mu } \omega ^{\mu })^4 \nonumber \\
&-&\frac{1}{4} \vec{R}^{\mu \nu }\vec{R}_{\mu \nu }+\frac{1}{2}m^{2}_{\rho }\vec{\rho }_{\mu }\vec{\rho \, }^{\mu } + \Lambda _{\omega } g_{\rho N}^2 \vec{\rho }_{\mu }\vec{\rho \,}^{\mu } g_{\omega N}^2 \omega _{\mu } \omega ^{\mu } \nonumber \\
&-&\frac{1}{4} P^{\mu \nu }P_{\mu \nu }+\frac{1}{2}m^{2}_{\phi }\phi _{\mu }\phi ^{\mu } -\frac{1}{4} F^{\mu \nu }F_{\mu \nu } ,
\end{eqnarray}$$
where Ψ
b
and ψ
l
stand for the baryonic and leptonic Dirac fields, respectively. The mesonic and electromagnetic field strength tensors are Ωμν = ∂μων − ∂νωμ,
![]() $\vec{R}_{\mu \nu }=\partial _{\mu }\vec{\rho }_{\nu }-\partial _{\nu }\vec{\rho }_{\mu }$
, P
μν = ∂μϕν − ∂νϕμ, and F
μν = ∂μ
A
ν − ∂ν
A
μ. The isospin operator is represented by the vector
$\vec{R}_{\mu \nu }=\partial _{\mu }\vec{\rho }_{\nu }-\partial _{\nu }\vec{\rho }_{\mu }$
, P
μν = ∂μϕν − ∂νϕμ, and F
μν = ∂μ
A
ν − ∂ν
A
μ. The isospin operator is represented by the vector
![]() $\vec{I}_b$
. The strong interaction coupling of a meson to a certain baryon is denoted by g (with N indicating nucleon) and the electromagnetic couplings by q, while the masses of the baryons, mesons, and leptons are denoted by m.
$\vec{I}_b$
. The strong interaction coupling of a meson to a certain baryon is denoted by g (with N indicating nucleon) and the electromagnetic couplings by q, while the masses of the baryons, mesons, and leptons are denoted by m.
The coupling constants of the above Lagrangian encode in an approximate way the complicated nuclear many-body dynamics. The g σN and g ωN couplings of the isoscalar σ and ω mesons to the nucleon determine the energy per particle and density of the nuclear matter saturation point, and, thus, are instrumental for the ground-state properties of finite nuclei. The g ρN coupling of the isovector ρ meson to the nucleon is key for the nuclear symmetry energy. Essentially, the symmetry energy measures the energy cost involved in changing all the protons into neutrons in nuclear matter (Li et al. Reference Li, Ramos, Verde and Vidana2014). Therefore, the g ρN coupling impacts on the properties of heavy neutron-rich nuclei and of neutron stars. The Lagrangian density (1), moreover, incorporates self-interactions of the meson fields. The σ-meson self-interactions, with the κ and λ couplings, were introduced by Boguta & Bodmer (Reference Boguta and Bodmer1977) and allowed for the first quantitatively successful descriptions of nuclear matter and finite nuclei within the relativistic theory. These couplings soften the EoS at moderate densities and allow one to obtain a realistic compressibility of nuclear matter (Boguta & Bodmer Reference Boguta and Bodmer1977; Boguta & Stoecker Reference Boguta and Stoecker1983) in agreement with the values extracted from experiments on nuclear giant resonances and HICs.Footnote 2 The quartic self-coupling ζ of the vector ω meson was introduced by Bodmer (Reference Bodmer1991). The ζ coupling must be non-negative to prevent abnormal solutions of the vector field equation of motion (Bodmer Reference Bodmer1991; Mueller & Serot Reference Mueller and Serot1996). It then implies an attractive non-linear interaction that softens the EoS for high densities (Bodmer Reference Bodmer1991), thereby directly affecting the structure and maximum mass of neutron stars (Mueller & Serot Reference Mueller and Serot1996). Finally, a mixed interaction between the ω and ρ mesons, with the coupling Λω, modulates the density dependence of the nuclear symmetry energy—which is related to the pressure of neutron matter—and influences the neutron radius of heavy nuclei and the radii of neutron stars (Horowitz & Piekarewicz Reference Horowitz and Piekarewicz2001a, Reference Horowitz and Piekarewicz2001b).
The Dirac equations for the different baryons and leptons are obtained from the Lagrangian density (1) as
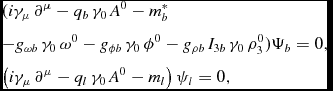 $$\begin{eqnarray}
&&(i\gamma _{\mu }\,\partial ^{\mu }-q_{b}\,{\gamma _{0}\,A^{0}}-m^{*}_{b} \nonumber \\
&&-g_{\omega b}\, \gamma _{0} \, \omega ^{0} -g_{\phi b} \,\gamma _{0}\, \phi ^{0} -g_{\rho b}\, I_{3 b}\, \gamma _{0} \,\rho _3^{0}) \Psi _{b}=0 , \nonumber \\
&&\left(i\gamma _{\mu }\,\partial ^{\mu }-q_{l}\,\gamma _{0} \,A^{0}-m_{l} \right) \psi _{l}=0 ,
\end{eqnarray}$$
$$\begin{eqnarray}
&&(i\gamma _{\mu }\,\partial ^{\mu }-q_{b}\,{\gamma _{0}\,A^{0}}-m^{*}_{b} \nonumber \\
&&-g_{\omega b}\, \gamma _{0} \, \omega ^{0} -g_{\phi b} \,\gamma _{0}\, \phi ^{0} -g_{\rho b}\, I_{3 b}\, \gamma _{0} \,\rho _3^{0}) \Psi _{b}=0 , \nonumber \\
&&\left(i\gamma _{\mu }\,\partial ^{\mu }-q_{l}\,\gamma _{0} \,A^{0}-m_{l} \right) \psi _{l}=0 ,
\end{eqnarray}$$
where the quantities
denote the effective masses of the baryons. Let us mention that only the time-like component of the vector fields and the third component of isospin have been written in Equation (2) due to the assumption of rotational invariance and charge conservation. The field equations of motion of the mesons follow from the respective Euler–Lagrange equations, see for example, Serot & Walecka (Reference Serot and Walecka1986). Altogether, the theory leads to a set of coupled non-linear field equations that involve strong couplings. The exact solution of these equations is extremely complicated if one attempts to quantise both the baryon fields and the meson fields. Physically, the baryons are the constituents of the nuclear medium, whereas the mesons are the carriers of the interaction between baryons. Thus, in order to be able to solve the equations of the theory, it is meaningful to replace the meson field operators by their expectation values, which then act as classical fields in which the baryons move. This approach is known as the RMF theory (Serot & Walecka Reference Serot and Walecka1986). Denoting the meson mean fields in uniform matter as
![]() $\bar{\sigma }= \langle \sigma \rangle$
,
$\bar{\sigma }= \langle \sigma \rangle$
,
![]() $\bar{\omega }=\langle \omega ^0\rangle$
,
$\bar{\omega }=\langle \omega ^0\rangle$
,
![]() $\bar{\rho }=\langle \rho _3^0\rangle$
, and
$\bar{\rho }=\langle \rho _3^0\rangle$
, and
![]() $\bar{\phi }=\langle \phi ^0\rangle$
, the mesonic equations of motion in the mean-field approximation for the uniform medium are
$\bar{\phi }=\langle \phi ^0\rangle$
, the mesonic equations of motion in the mean-field approximation for the uniform medium are
 $$\begin{eqnarray}
&&m_\sigma ^2 \, \bar{\sigma }+ \frac{\kappa }{2} g_{\sigma N}^3 \bar{\sigma }^2 + \frac{\lambda }{3!} g_{\sigma N}^4 \bar{\sigma }^3 = \sum _{b} g_{\sigma b} n_b^s , \nonumber \\
&& m_\omega ^2 \, \bar{\omega }+ \frac{\zeta }{3!} g_{\omega N}^4 \bar{\omega }^3 + 2 \Lambda _{\omega } g_{\rho N\,}^2 g_{\omega N}^2 \bar{\rho }^2 \bar{\omega }= \sum _{b} g_{\omega b} n_b , \nonumber \\
&& m_\rho ^2 \, \bar{\rho }+ 2 \Lambda _{\omega } g_{\rho N}^2 g_{\omega N}^2 \bar{\omega }^2 \bar{\rho }= \sum _{b} g_{\rho b} I_{3 b} n_b , \nonumber \\
&& m_\phi ^2 \bar{\phi }\, = \sum _{b} g_{\phi b} n_b ~,
\end{eqnarray}$$
$$\begin{eqnarray}
&&m_\sigma ^2 \, \bar{\sigma }+ \frac{\kappa }{2} g_{\sigma N}^3 \bar{\sigma }^2 + \frac{\lambda }{3!} g_{\sigma N}^4 \bar{\sigma }^3 = \sum _{b} g_{\sigma b} n_b^s , \nonumber \\
&& m_\omega ^2 \, \bar{\omega }+ \frac{\zeta }{3!} g_{\omega N}^4 \bar{\omega }^3 + 2 \Lambda _{\omega } g_{\rho N\,}^2 g_{\omega N}^2 \bar{\rho }^2 \bar{\omega }= \sum _{b} g_{\omega b} n_b , \nonumber \\
&& m_\rho ^2 \, \bar{\rho }+ 2 \Lambda _{\omega } g_{\rho N}^2 g_{\omega N}^2 \bar{\omega }^2 \bar{\rho }= \sum _{b} g_{\rho b} I_{3 b} n_b , \nonumber \\
&& m_\phi ^2 \bar{\phi }\, = \sum _{b} g_{\phi b} n_b ~,
\end{eqnarray}$$
where I 3b is the third component of the isospin of a given baryon, and we use the convention that for protons I 3p = +1/2. The quantities
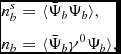 $$\begin{eqnarray}
n_b^s &=& \langle \bar{\Psi }_b \Psi _b \rangle , \nonumber \\
n_b &=& \langle \bar{\Psi }_b\gamma ^0 \Psi _b\rangle ,
\end{eqnarray}$$
$$\begin{eqnarray}
n_b^s &=& \langle \bar{\Psi }_b \Psi _b \rangle , \nonumber \\
n_b &=& \langle \bar{\Psi }_b\gamma ^0 \Psi _b\rangle ,
\end{eqnarray}$$
are, respectively, the scalar and vector densities for the b baryon. In terms of the baryonic and leptonic Fermi momenta, k Fb and k Fl, and of the respective Fermi energies
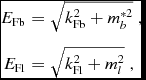 $$\begin{eqnarray}
E_{\text{Fb}}&=&\sqrt{k_{\text{Fb}}^{2}+m^{*2}_{b}} \ , \nonumber \\
E_{\text{Fl}}&=& \sqrt{k_{\text{Fl}}^{2}+m^{2}_{l} } \ ,
\end{eqnarray}$$
$$\begin{eqnarray}
E_{\text{Fb}}&=&\sqrt{k_{\text{Fb}}^{2}+m^{*2}_{b}} \ , \nonumber \\
E_{\text{Fl}}&=& \sqrt{k_{\text{Fl}}^{2}+m^{2}_{l} } \ ,
\end{eqnarray}$$
the scalar and vector densities for the baryons and the vector densities for the leptons are expressed as
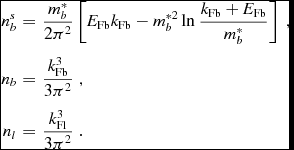 $$\begin{eqnarray}
n^{s}_{b}&=&\frac{m^{*}_{b}}{2\pi ^{2}} \left[E_{\text{Fb}}k_{\text{Fb}}-{m}^{*2}_{b}\ln \frac{k_{\text{Fb}}+E_{\text{Fb}}}{m^{*}_{b}} \right] \ , \nonumber \\
n_{b}&=&\frac{k_{\text{Fb}}^{3}}{3\pi ^{2}} \ , \nonumber \\
n_{l}&=&\frac{k_{\text{Fl}}^{3}}{3\pi ^{2}} \ .
\end{eqnarray}$$
$$\begin{eqnarray}
n^{s}_{b}&=&\frac{m^{*}_{b}}{2\pi ^{2}} \left[E_{\text{Fb}}k_{\text{Fb}}-{m}^{*2}_{b}\ln \frac{k_{\text{Fb}}+E_{\text{Fb}}}{m^{*}_{b}} \right] \ , \nonumber \\
n_{b}&=&\frac{k_{\text{Fb}}^{3}}{3\pi ^{2}} \ , \nonumber \\
n_{l}&=&\frac{k_{\text{Fl}}^{3}}{3\pi ^{2}} \ .
\end{eqnarray}$$
With the above ingredients, one can compute the energy density and the pressure of the system. The energy density is given by
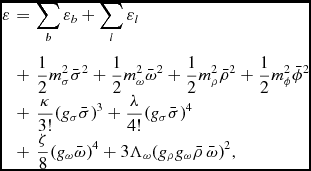 $$\begin{eqnarray}
\varepsilon &=&\sum _{b} \varepsilon _{b}+\sum _{l}\varepsilon _{l} \nonumber \\
&+&\frac{1}{2}m^{2}_{\sigma } \bar{\sigma }^{2}+\frac{1}{2}m^{2}_{\omega } \bar{\omega }^{2}+\frac{1}{2}m^{2}_{\rho } \bar{\rho }^{2} +\frac{1}{2}m^{2}_{\phi } \bar{\phi }^{2}\cr &+& \frac{\kappa }{3 !} (g_{\sigma } \bar{\sigma })^ 3+ \frac{\lambda }{4 !} (g_{\sigma } \bar{\sigma })^ 4 \cr &+& \frac{\zeta }{8} (g_{\omega } \bar{\omega })^4 + 3 \Lambda _{\omega } (g_{\rho } g_{\omega } \bar{\rho }\, \bar{\omega }) ^2 ,
\end{eqnarray}$$
$$\begin{eqnarray}
\varepsilon &=&\sum _{b} \varepsilon _{b}+\sum _{l}\varepsilon _{l} \nonumber \\
&+&\frac{1}{2}m^{2}_{\sigma } \bar{\sigma }^{2}+\frac{1}{2}m^{2}_{\omega } \bar{\omega }^{2}+\frac{1}{2}m^{2}_{\rho } \bar{\rho }^{2} +\frac{1}{2}m^{2}_{\phi } \bar{\phi }^{2}\cr &+& \frac{\kappa }{3 !} (g_{\sigma } \bar{\sigma })^ 3+ \frac{\lambda }{4 !} (g_{\sigma } \bar{\sigma })^ 4 \cr &+& \frac{\zeta }{8} (g_{\omega } \bar{\omega })^4 + 3 \Lambda _{\omega } (g_{\rho } g_{\omega } \bar{\rho }\, \bar{\omega }) ^2 ,
\end{eqnarray}$$
where the energy densities of baryons and leptons take the expressions
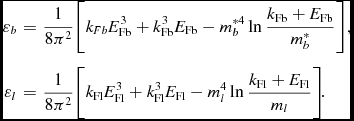 $$\begin{eqnarray}
\varepsilon _{b}& = &\frac{1}{8\pi ^ {2}}\bigg [k_{Fb}E_{\text{Fb}}^{3}+k_{\text{Fb}}^{3} E_{\text{Fb}} - {m}^{*4}_{b}\ln \frac{k_{\text{Fb}}+E_{\text{Fb}}}{{m}^{*}_{b}} \bigg ] , \nonumber \\
\varepsilon _{l}& = &\frac{1}{8\pi ^ {2}}\bigg [k_{\text{Fl}}E_{\text{Fl}}^{3}+k_{\text{Fl}}^{3} E_{\text{Fl}} - m^{4}_{l}\ln \frac{k_{\text{Fl}}+E_{\text{Fl}}}{m_{l}} \bigg ] \!.
\end{eqnarray}$$
$$\begin{eqnarray}
\varepsilon _{b}& = &\frac{1}{8\pi ^ {2}}\bigg [k_{Fb}E_{\text{Fb}}^{3}+k_{\text{Fb}}^{3} E_{\text{Fb}} - {m}^{*4}_{b}\ln \frac{k_{\text{Fb}}+E_{\text{Fb}}}{{m}^{*}_{b}} \bigg ] , \nonumber \\
\varepsilon _{l}& = &\frac{1}{8\pi ^ {2}}\bigg [k_{\text{Fl}}E_{\text{Fl}}^{3}+k_{\text{Fl}}^{3} E_{\text{Fl}} - m^{4}_{l}\ln \frac{k_{\text{Fl}}+E_{\text{Fl}}}{m_{l}} \bigg ] \!.
\end{eqnarray}$$
We note that in obtaining Equation (8) for the energy density, the equations of motion (4) were used to rewrite the contribution to ε of
![]() $\sum _{b} ( g_{\omega b} \bar{\omega }n_b + g_{\rho b} \bar{\rho }I_{3 b} n_b + g_{\phi b} \bar{\phi }n_b)$
. Finally, the pressure can be computed using the thermodynamic relation
$\sum _{b} ( g_{\omega b} \bar{\omega }n_b + g_{\rho b} \bar{\rho }I_{3 b} n_b + g_{\phi b} \bar{\phi }n_b)$
. Finally, the pressure can be computed using the thermodynamic relation
where the baryonic and leptonic chemical potentials are given by
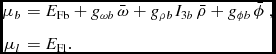 $$\begin{eqnarray}
\mu _{b}&=& E_{\text{Fb}}+g_{\omega b} \, \bar{\omega }+g_{\rho b} \,I_{3 b} \,\bar{\rho }+g_{\phi b} \,\bar{\phi }\ , \nonumber \\
\mu _{l} &=& E_{\text{Fl}}.
\end{eqnarray}$$
$$\begin{eqnarray}
\mu _{b}&=& E_{\text{Fb}}+g_{\omega b} \, \bar{\omega }+g_{\rho b} \,I_{3 b} \,\bar{\rho }+g_{\phi b} \,\bar{\phi }\ , \nonumber \\
\mu _{l} &=& E_{\text{Fl}}.
\end{eqnarray}$$
The cores of neutron stars harbour globally neutral matter that is in β-equilibrium. Therefore, the chemical potentials and the number densities of the different particles in a neutron star core are related by the conditions:
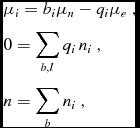 $$\begin{eqnarray}
&&\mu _i=b_i \mu _n- q_i \mu _e \ ,\nonumber \\
&&0=\sum _{b,l} q_i \, n_i \ , \nonumber \\
&& n=\sum _{b} n_i \ ,
\end{eqnarray}$$
$$\begin{eqnarray}
&&\mu _i=b_i \mu _n- q_i \mu _e \ ,\nonumber \\
&&0=\sum _{b,l} q_i \, n_i \ , \nonumber \\
&& n=\sum _{b} n_i \ ,
\end{eqnarray}$$
where b i and q i denote, respectively, the baryon number and the charge of the particle i. These relations, the Dirac equations (2) for the baryons and leptons, and the field equations (4) for the mesonic fields σ, ω, ρ, and ϕ, are to be solved self-consistently for a given total baryon density n. Once the chemical potential and the density of each species have been obtained at the given n, one can determine the energy density and pressure of the neutron star matter for each density.
3 MODELS FOR THE EQUATION OF STATE
From the Lagrangian (1), in Tolos et al. (Reference Tolos, Centelles and Ramos2017), we formulated the models FSU2R (with nucleons) and FSU2H (with nucleons and hyperons), with a motivation for accommodating massive enough stars and the new astrophysical measurements of small stellar radii within a self-consistent microscopic theory of the EoS for the core of neutron stars. Note that this type of approach is different from—but complementary to—the methods where the astrophysical and nuclear observables are mapped onto the EoS through piecewise parameterisations of the EoS (Raithel, Ozel, & Psaltis Reference Raithel, Ozel and Psaltis2016; Lattimer & Prakash Reference Lattimer and Prakash2016; Ozel & Freire Reference Ozel and Freire2016). To build our models, we started from the nucleonic FSU2 model of Chen & Piekarewicz (Reference Chen and Piekarewicz2014) that reproduces heavy neutron star masses but was not constrained to radii. The condition of small stellar radii imposed a soft nuclear symmetry energy in the theory. We showed that the resulting FSU2R and FSU2H models, besides the mentioned astrophysical constraints, can successfully describe the properties of finite nuclei and conform to the constraints on the nuclear EoS from kaon production and collective flow in HICs (Fuchs et al. Reference Fuchs, Faessler, Zabrodin and Zheng2001; Lynch et al. Reference Lynch, Tsang, Zhang, Danielewicz, Famiano, Li and Steiner2009; Danielewicz et al. Reference Danielewicz, Lacey and Lynch2002).
In the present work, we start by introducing a modification of the parameters of our models FSU2R and FSU2H of Tolos et al. (Reference Tolos, Centelles and Ramos2017) in order to refine the behaviour of the EoS of PNM in the region of subsaturation densities. We report the new version of the parameters in Table 1 (it should be mentioned that the form of the equations of motion remains the same irrespective of the specific values of the coupling constants). We have changed the value of the quartic isovector–vector coupling Λω of FSU2R and FSU2H from 0.05 in Tolos et al. (Reference Tolos, Centelles and Ramos2017) to 0.045. This has been done because it results in a symmetry energy that is a little stiffer than before and avoids a previous instability in the EoS of PNM for low subsaturation densities. As Λω has been changed, we have refitted accordingly the value of the coupling g 2 ρN between the ρ-meson and the nucleons to obtain the same good reproduction of binding energies and charge radii of finite nuclei as in Tolos et al. (Reference Tolos, Centelles and Ramos2017). The values of the other parameters of FSU2R and FSU2H are the same of Tolos et al. (Reference Tolos, Centelles and Ramos2017). Owing to the fact the Λω and g 2 ρN couplings only contribute in neutron-rich matter, the EoS of symmetric nuclear matter (SNM), composed of the same number of protons and neutrons, is identical to that of our models FSU2R and FSU2H in Tolos et al. (Reference Tolos, Centelles and Ramos2017).
Table 1. Parameters of the models FSU2R and FSU2H of this work. The mass of the nucleon is m N = 939 MeV.

We collect in Table 2 a few characteristic isoscalar and isovector properties at the nuclear matter saturation density n 0 for the present version of our models. In the work (Fortin et al. Reference Fortin, Zdunik, Haensel and Bejger2015), the authors derived the constraint 1.7 ≲ P(n 0) ≲ 2.8 MeV fm−3 for the pressure of neutron star matter at saturation density. They deduced this constraint from the results of the microscopic calculations of PNM performed by Hebeler et al. (Reference Hebeler, Lattimer, Pethick and Schwenk2013) using chiral two-nucleon and three-nucleon interactions, which are in good agreement with the results by Gandolfi, Carlson, & Reddy (Reference Gandolfi, Carlson and Reddy2012) from Quantum Monte Carlo calculations with the Argonne v 18 nucleon–nucleon potential plus three-nucleon forces. A narrower range 2.3 ≲ P(n 0) ≲ 2.6 MeV fm−3 was estimated more recently by Hagen et al. (Reference Hagen2015) from ab initio calculations of nuclear systems with chiral interactions. While our models FSU2R and FSU2H of Tolos et al. (Reference Tolos, Centelles and Ramos2017), with PNM pressures at saturation of 2.27 and 2.06 MeV fm−3, fulfil the constraint of Fortin et al. (Reference Fortin, Zdunik, Haensel and Bejger2015), they are somewhat below the constraint of Hagen et al. (Reference Hagen2015). Now, with the new parameterisation of our models, we are able to obtain PNM pressures at saturation density of 2.44 MeV fm−3 in FSU2R and of 2.30 MeV fm−3 in FSU2H (see Table 2) that are consistent with both the predictions from chiral forces derived by Fortin et al. (Reference Fortin, Zdunik, Haensel and Bejger2015) and Hagen et al. (Reference Hagen2015).
Table 2. Properties at saturation of the models FSU2R and FSU2H of this work. We show the saturation density (n 0), energy per particle (E/A), compressibility (K), and effective nucleon mass (m* N /mN ) in symmetric nuclear matter, as well as the symmetry energy (E sym), slope of the symmetry energy (L), curvature of the symmetry energy (K sym), and pressure of pure neutron matter (P PNM) at n 0.

The EoS of PNM of the present FSU2R and FSU2H models differs from the results we showed in Tolos et al. (Reference Tolos, Centelles and Ramos2017) almost only for densities in the low-density region n ≲ n 0, where the pressure of PNM is a little higher now. However, above saturation density, the pressures of our current parameters and those of Tolos et al. (Reference Tolos, Centelles and Ramos2017) are very similar. Consequently, compared with Tolos et al. (Reference Tolos, Centelles and Ramos2017), one may anticipate that the predictions for masses and radii of neutron stars will not be drastically affected.
The slope parameter L of the symmetry energy, i.e.,
![]() $\displaystyle L = 3 n_0 \Big ( \frac{\partial E_{\rm sym}(n)}{\partial n} \Big )_{n_0}$
, has become a standard reference in the literature for characterising the stiffness of the change of the nuclear symmetry energy E
sym(n) with density. In our original version of the FSU2R and FSU2H models shown in Tolos et al. (Reference Tolos, Centelles and Ramos2017), the value of the symmetry energy at saturation density was E
sym(n
0) = 30.2 MeV in both models, while the slope parameter was L = 44.3 MeV in FSU2R and L = 41 MeV in FSU2H. In the updated version of FSU2R and FSU2H of the present work, these properties become E
sym(n
0) = 30.7 MeV and L = 46.9 MeV in FSU2R and E
sym(n
0) = 30.5 MeV and L = 44.5 MeV in FSU2H (see Table 2). These values suggest a relatively soft nuclear symmetry energy. We have plotted in Figure 1 the ranges for E
sym(n
0) and L that have been estimated in several recent works through the analysis of a variety of nuclear data from terrestrial experiments, astrophysical observations, and theoretical calculations (Li & Han Reference Li and Han2013; Lattimer & Lim Reference Lattimer and Lim2013; Roca-Maza et al. Reference Roca-Maza, Viñas, Centelles, Agrawal, Colo’, Paar, Piekarewicz and Vretenar2015; Hagen et al. Reference Hagen2015; Oertel et al. Reference Oertel, Hempel, Klähn and Typel2017; Birkhan et al. Reference Birkhan2017). It can be seen that the predictions of FSU2R and FSU2H have an overlap with the majority of these ranges. We would like to remark that this is an a posteriori result, because the predicted values of E
sym(n
0) and L are the consequence (Tolos et al. Reference Tolos, Centelles and Ramos2017) of having adjusted the FSU2R and FSU2H parameter sets to reproduce neutron star radii of about 13 km, without sacrificing maximum masses of 2M⊙ nor the description of binding energies and charge radii of atomic nuclei. Hence, we interpret the reasonable agreement of our results with the multiple constraints in Figure 1 as hinting at the plausibility of the existence of neutron stars with relatively small radii.
$\displaystyle L = 3 n_0 \Big ( \frac{\partial E_{\rm sym}(n)}{\partial n} \Big )_{n_0}$
, has become a standard reference in the literature for characterising the stiffness of the change of the nuclear symmetry energy E
sym(n) with density. In our original version of the FSU2R and FSU2H models shown in Tolos et al. (Reference Tolos, Centelles and Ramos2017), the value of the symmetry energy at saturation density was E
sym(n
0) = 30.2 MeV in both models, while the slope parameter was L = 44.3 MeV in FSU2R and L = 41 MeV in FSU2H. In the updated version of FSU2R and FSU2H of the present work, these properties become E
sym(n
0) = 30.7 MeV and L = 46.9 MeV in FSU2R and E
sym(n
0) = 30.5 MeV and L = 44.5 MeV in FSU2H (see Table 2). These values suggest a relatively soft nuclear symmetry energy. We have plotted in Figure 1 the ranges for E
sym(n
0) and L that have been estimated in several recent works through the analysis of a variety of nuclear data from terrestrial experiments, astrophysical observations, and theoretical calculations (Li & Han Reference Li and Han2013; Lattimer & Lim Reference Lattimer and Lim2013; Roca-Maza et al. Reference Roca-Maza, Viñas, Centelles, Agrawal, Colo’, Paar, Piekarewicz and Vretenar2015; Hagen et al. Reference Hagen2015; Oertel et al. Reference Oertel, Hempel, Klähn and Typel2017; Birkhan et al. Reference Birkhan2017). It can be seen that the predictions of FSU2R and FSU2H have an overlap with the majority of these ranges. We would like to remark that this is an a posteriori result, because the predicted values of E
sym(n
0) and L are the consequence (Tolos et al. Reference Tolos, Centelles and Ramos2017) of having adjusted the FSU2R and FSU2H parameter sets to reproduce neutron star radii of about 13 km, without sacrificing maximum masses of 2M⊙ nor the description of binding energies and charge radii of atomic nuclei. Hence, we interpret the reasonable agreement of our results with the multiple constraints in Figure 1 as hinting at the plausibility of the existence of neutron stars with relatively small radii.
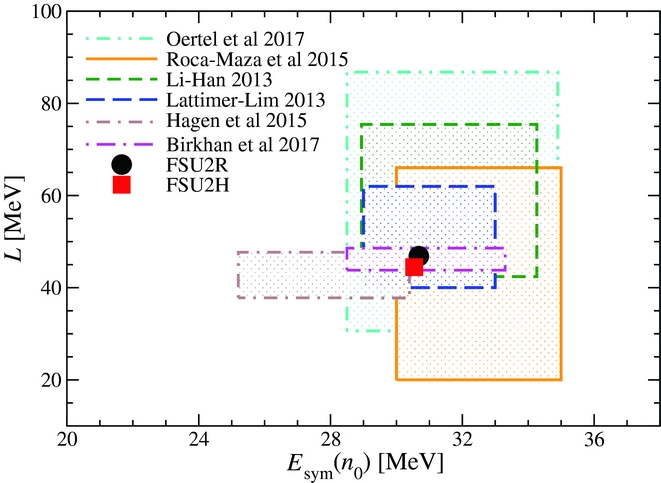
Figure 1. Slope of the symmetry energy (L) versus symmetry energy [E sym(n 0)] at the nuclear matter saturation density for the models FSU2R and FSU2H discussed in text. The shaded regions depict the determinations from Li & Han (Reference Li and Han2013), Lattimer & Lim (Reference Lattimer and Lim2013), Roca-Maza et al. (Reference Roca-Maza, Viñas, Centelles, Agrawal, Colo’, Paar, Piekarewicz and Vretenar2015), Hagen et al. (Reference Hagen2015), Oertel et al. (Reference Oertel, Hempel, Klähn and Typel2017), and Birkhan et al. (Reference Birkhan2017).
The neutron matter EoS is also strongly related with the neutron distribution in atomic nuclei. Models with softer symmetry energies produce a thinner neutron skin Δr np (difference between the rms radii of the neutron and proton density distributions) in nuclei (Alex Brown Reference Alex Brown2000; Horowitz & Piekarewicz Reference Horowitz and Piekarewicz2001a). Unfortunately, neutron densities and neutron radii are poorly known to date because the distribution of neutrons in a nucleus is hard to measure. Our present FSU2R and FSU2H models predict a neutron skin thickness of 0.15 fm in the neutron-rich nucleus 208Pb. This prediction is compatible with the range 0.13 ≲ Δr np ≲ 0.19 fm for 208Pb extracted in Roca-Maza et al. (Reference Roca-Maza, Viñas, Centelles, Agrawal, Colo’, Paar, Piekarewicz and Vretenar2015) from measurements of the electric dipole polarisability of nuclei, the value Δr np = 0.15 ± 0.03 fm determined from coherent pion photoproduction in 208Pb at the MAMI facility (Tarbert et al. Reference Tarbert2014), and the value Δr np = 0.302 ± 0.177 fm from parity violating electron scattering on 208Pb performed at JLab (Abrahamyan et al. Reference Abrahamyan2012; Horowitz et al. Reference Horowitz2012).Footnote 3 In the case of the lighter nucleus 48Ca, we find a neutron radius of 3.55 fm with FSU2R and of 3.57 fm with FSU2H, and a neutron skin of 0.166 fm with both models. The prediction is in good accord with the ranges 3.47–3.60 fm for the neutron radius and 0.12–0.15 fm for the neutron skin of 48Ca obtained in Hagen et al. (Reference Hagen2015) through ab initio calculations of the neutron distribution of 48Ca using nuclear interactions derived from chiral effective field theory; it also is in accord with the neutron skin of 0.14–0.20 fm for 48Ca found from the new measurement of the electric dipole polarisability in 48Ca (Birkhan et al. Reference Birkhan2017). Altogether, it appears that the properties of the symmetry energy of the proposed models for the EoS, which are motivated by reproducing small neutron star radii (see next section), are compatible within uncertainties with different empirical and theoretical extractions of these properties.
4 STELLAR PROPERTIES
Having access to the pressure and energy density of matter, we can compute the properties of neutron stars by solving the Tolman–Oppenheimer–Volkoff (TOV) equations (Oppenheimer & Volkoff Reference Oppenheimer and Volkoff1939). For static and spherically symmetric stars, the TOV equations read as
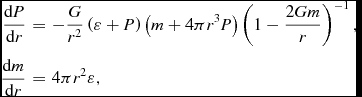 $$\begin{eqnarray}
\frac{\text{d}P}{\text{d}r}&=&-\frac{G}{r^2}\left(\varepsilon +P\right) \left(m+4\pi r^3 P\right)\left(1-\frac{2Gm}{r}\right)^{-1} , \nonumber \\
\frac{\text{d}m}{\text{d}r}&=&4 \pi r^2 \varepsilon ,
\end{eqnarray}$$
$$\begin{eqnarray}
\frac{\text{d}P}{\text{d}r}&=&-\frac{G}{r^2}\left(\varepsilon +P\right) \left(m+4\pi r^3 P\right)\left(1-\frac{2Gm}{r}\right)^{-1} , \nonumber \\
\frac{\text{d}m}{\text{d}r}&=&4 \pi r^2 \varepsilon ,
\end{eqnarray}$$
where r is the radial coordinate, m is the mass enclosed by a radius r, and G is the gravitational constant. For a given central density, the integration of these equations provides the corresponding mass and radius of the star. By repeating the calculation for different central densities, the mass–radius (M–R) relation of neutron stars can be obtained.
Indeed, to solve the TOV equations for a neutron star, we need the EoS of matter over a wide range of densities from the centre to the surface of the star. The structure of a neutron star is such that the heavy liquid core is surrounded by a thin solid crust (Shapiro & Teukolsky Reference Shapiro and Teukolsky1983; Haensel, Potekhin, & Yakovlev Reference Haensel, Potekhin and Yakovlev2006). The transition from the core to the crust occurs when the density of matter becomes lower than approximately 1.5 × 1014 g cm−3. Below this density, matter ceases to exist in a homogeneous liquid phase because it is favourable that the protons concentrate with neutrons in nuclear clusters, which arrange themselves in a crystal lattice in order to minimise the Coulomb repulsion among them (Baym, Bethe, & Pethick Reference Baym, Bethe and Pethick1971b; Baym, Pethick, & Sutherland Reference Baym, Pethick and Sutherland1971a; Shapiro & Teukolsky Reference Shapiro and Teukolsky1983; Haensel et al. Reference Haensel, Potekhin and Yakovlev2006). In the inner layers of the crust, the nuclear clusters are beyond the neutron drip point and the lattice is permeated by a gas of free neutrons in addition to the electron gas, whereas in the outer crust the nuclear clusters are neutron-rich nuclei below the neutron drip point, embedded in the electron gas. We have solved the TOV equations using the FSU2R and FSU2H models for the EoS of the uniform matter of the liquid core of the star for densities above 0.09 fm−3 (≈1.5 × 1014 g cm−3), under the conditions of β-equilibrium and global charge neutrality expressed in Equation (12) of Section 2. At the densities of the crust, in the absence of calculations with our models of the complex structures that can populate this region of the star, we have used the EoS for the crust of neutron stars that has recently been derived from calculations based on the Brueckner theory in Sharma et al. (Reference Sharma, Centelles, Viñas, Baldo and Burgio2015).
The FSU2R model applies to nucleonic cores of neutron stars, i.e., when the whole stellar core is assumed to consist of neutrons, protons, electrons, and muons (‘npeμ’ matter). In the dense inner region of a neutron star core, however, the chemical potential may become so high that matter will be able to undergo a transition to other states of the low-lying octet of baryons, with hyperons appearing in the composition (‘npYeμ’ matter). Thus, we have devised the FSU2H model to allow for the presence of hyperons in the star interior (Tolos et al. Reference Tolos, Centelles and Ramos2017). In consequence, in the case of the FSU2H EoS, besides the nucleon and meson couplings shown in Table 1, we have considered the complete octet of baryons in the Lagrangian density (1). We have fixed the corresponding hyperon couplings from SU(3) flavour symmetry and from information on hyperon optical potentials in hypernuclei. We leave for the next section the discussion of the determination of the hyperon couplings and the analysis of the influence of the uncertainties associated with these couplings. Here, we focus on the results for the masses and sizes of neutron stars from the FSU2R nucleonic EoS and from the FSU2H hyperonic EoS with our baseline values for the hyperon couplings (given in Section 5).
We display the results for the relation between mass and radius of neutron stars in Figure 2. A few data on the maximum mass configuration and the 1.5M⊙ configuration from FSU2R and FSU2H are presented in Table 3. For completeness, in Figure 2, besides the curves of FSU2R and FSU2H, we also plot the M–R relations of two popular EoSs widely used in astrophysical calculations. They correspond to the Shen et al. EoS based on the relativistic TM1 nuclear mean field model (Shen et al. Reference Shen, Toki, Oyamatsu and Sumiyoshi1998) and to the Lattimer–Swesty EoS based on a non-relativistic Skyrme nuclear force (in its Ska version) (Lattimer & Swesty Reference Lattimer and Swesty1991). Also shown is the result of the recent EoS from the Brueckner theory with the Argonne v 18 potential plus three-body forces computed with the Urbana model (Sharma et al. Reference Sharma, Centelles, Viñas, Baldo and Burgio2015). These additional EoSs are all non-hyperonic. We have included in the same Figure 2 a few recent astrophysical determinations of neutron star M–R limits.

Figure 2. Mass versus radius for neutron stars from the models FSU2R and FSU2H of this work and from some models from the literature [Shen: (Shen et al. Reference Shen, Toki, Oyamatsu and Sumiyoshi1998), L&S: (Lattimer & Swesty Reference Lattimer and Swesty1991), Brueckner: (Sharma et al. Reference Sharma, Centelles, Viñas, Baldo and Burgio2015)]. The thin horizontal bands indicate the heaviest observed masses M = 1.97 ± 0.04M⊙ (Demorest et al. Reference Demorest, Pennucci, Ransom, Roberts and Hessels2010) and M = 2.01 ± 0.04M⊙ (Antoniadis et al. Reference Antoniadis2013). The vertical blue band at the back depicts the M–R region constrained in Hebeler et al. (Reference Hebeler, Lattimer, Pethick and Schwenk2013) from chiral nuclear interactions up to n = 1.1n 0 and the conditions of M max > 1.97M⊙ and causality. The vertical red band at the front shows the M–R region derived from five quiescent low-mass X-ray binaries and five photospheric radius expansion X-ray bursters after a Bayesian analysis (Lattimer & Steiner Reference Lattimer and Steiner2014b). The vertical striped yellow band is the M–R constraint derived from the cooling tails of type-I X-ray bursts in three low-mass X-ray binaries and a Bayesian analysis in Nättilä et al. (Reference Nättilä, Steiner, Kajava, Suleimanov and Poutanen2016) (model A of the paper).
Table 3. Properties of the maximum mass and 1.5M⊙ configurations for nucleonic (npeμ) neutron stars calculated with the FSU2R EoS and for hyperonic (npYeμ) neutron stars calculated with the FSU2H EoS. From top to bottom, mass, radius, compactness parameter GM/Rc 2, surface gravitational red shift z surf = (1 − 2GM/Rc 2)−1/2 − 1, and the values of the number density, pressure, and mass-energy density at the centre of the star.
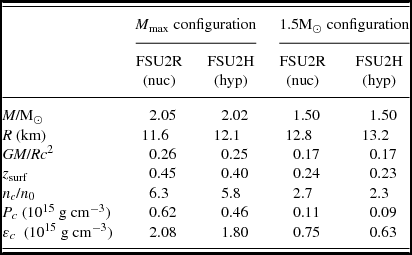
The M–R curve from each EoS exhibits a maximum mass, beyond which the star would become unstable against collapse into a black hole. The heaviest known masses of neutron stars are M = 1.97 ± 0.04M⊙ in the PSR J1614–2230 pulsar (Demorest et al. Reference Demorest, Pennucci, Ransom, Roberts and Hessels2010) and M = 2.01 ± 0.04M⊙ in the PSR J0348+0432 pulsar (Antoniadis et al. Reference Antoniadis2013). We depict them by the horizontal bands in Figure 2. Both the nucleonic FSU2R EoS and the hyperonic FSU2H EoS are able to provide maximum masses fulfilling the ≈2M⊙ observational limit, as well as the other EoSs shown in the same figure. We note that FSU2R reaches the maximum mass with a fairly compact stellar radius of 11.6 km (see Table 3). For canonical neutron stars with masses of 1.4–1.5M⊙, FSU2R predicts a radius of 12.8 km. The recent astrophysical determinations of neutron star radii from quiescent low-mass X-ray binaries in globular clusters and X-ray bursters seem to point in this direction (Guillot et al. Reference Guillot, Servillat, Webb and Rutledge2013; Guillot & Rutledge Reference Guillot and Rutledge2014; Guver & Ozel Reference Guver and Ozel2013; Heinke et al. Reference Heinke2014; Lattimer & Steiner Reference Lattimer and Steiner2014a, Reference Lattimer and Steiner2014b; Ozel et al. Reference Ozel, Psaltis, Guver, Baym, Heinke and Guillot2016). Although these determinations are indirect and depend on stellar atmosphere models, they overall converge in favouring small neutron star radii in the range of about 9–13 km (Lattimer & Prakash Reference Lattimer and Prakash2016; Ozel & Freire Reference Ozel and Freire2016). An accurate radius measurement by new observatories such as NICER (Arzoumanian et al. Reference Arzoumanian, Takahasi, den Herder and Bautz2014), which has begun operating aboard the International Space Station in 2017 June, would represent a major step forward to corroborate or modify these expectations.
The compromise between having large maximum masses and small radii for canonical neutron stars is a challenging constraint that rules out a large number of theoretical EoSs (Lattimer & Prakash Reference Lattimer and Prakash2016; Ozel & Freire Reference Ozel and Freire2016; Oertel et al. Reference Oertel, Hempel, Klähn and Typel2017). This follows from the fact that the pressure of the high-density EoS must be hard enough to sustain massive stars, whereas the pressure at 1–2 times the nuclear saturation density n 0 must be, in contrast, effectively soft in order to produce small radii for canonical mass stars. Given that the pressure of neutron star matter in the vicinity of n 0 is basically governed by the nuclear symmetry energy, the challenge is particularly acute in relativistic field theoretical models because the relativistic models usually have stiff symmetry energies. As we have demonstrated with FSU2R, it is possible to obtain parameterisations of the considered relativistic Lagrangian that meet both large stellar masses and—on condition of a soft symmetry energy—radii smaller than ~13 km for M ≳ 1.4M⊙, and that still provide an excellent reproduction of the binding energies and charge radii of finite nuclei (Tolos et al. Reference Tolos, Centelles and Ramos2017). There are some other parameterisations in the frame of the relativistic field theory that support these findings, such as the recent RMF012 and RMF016 models of Chen & Piekarewicz (Reference Chen and Piekarewicz2015b, Reference Chen and Piekarewicz2015a). Indeed, the accurately calibrated RMF016 model produces neutron stars of 2M⊙ and gives radii of 13 km for stars of 1.4M⊙ (Chen & Piekarewicz Reference Chen and Piekarewicz2015b, Reference Chen and Piekarewicz2015a), in keeping with the predictions of our FSU2R EoS.
When we allow for the appearance of hyperons in the neutron star core with the FSU2R model, the maximum mass of the star experiences a reduction of the order of 15%, due to the expected softening of the EoS, and then, with a maximum mass of 1.77M⊙, it falls short of the 2M⊙ limit. In an effort to shed some light on the question whether with exotic degrees of freedom in the core, the star can satisfy the targets of 2M⊙ maximum mass and small radius at canonical mass, we have developed the hyperonic model FSU2H. In FSU2H, we essentially have stiffened further the nucleonic pressure above twice the saturation density, i.e., around the onset of appearance of hyperons. This comes at the price of a certain overpressure in SNM for densities n ≳ 2n 0 when we compare it with the constraints deduced from the modelling of collective flow in HICs (Danielewicz et al. Reference Danielewicz, Lacey and Lynch2002), cf. Figure 1 of Tolos et al. (Reference Tolos, Centelles and Ramos2017). Yet, the pressure of FSU2H in PNM, shown also in Figure 1 of Tolos et al. (Reference Tolos, Centelles and Ramos2017), fits within the projected region from the collective flow studies. Given that the β-equilibrated neutron-star matter is highly asymmetric, we consider this model as sufficiently realistic for describing neutron stars. The determination of narrower constraints on the EoS of PNM at several times n 0 from HIC experiments (Russotto et al. Reference Russotto2016) in the future should be of great help in this regard.
It can be observed in Figure 2 that the FSU2H model with hyperons produces a comparable M–R relation to FSU2R and satisfies, as mentioned, the observational limit of 2M⊙. With respect to FSU2R, in FSU2H, the size of the radii has increased by 0.2–0.5 km for neutron stars heavier than 1M⊙, expectedly, from the stiffer pressure of the nucleonic sector above twice the saturation density. The onset of hyperons occurs at a baryon density of 0.33 fm−3, or 2.2n 0. The maximum mass of 2.02M⊙ calculated with FSU2H is characterised by a radius of 12.1 km (see Table 3). For 1.5M⊙ stars, the hyperonic FSU2H EoS predicts radii of 13.2 km, which, although on the upper edge, are still compatible with the recent astrophysical indications of neutron star radii of about 9–13 km (Lattimer & Prakash Reference Lattimer and Prakash2016; Ozel & Freire Reference Ozel and Freire2016). The numerical results for the EoS and M–R relation of the FSU2R and FSU2H models are tabulated in the Appendix.
In closing this section, we ought to mention that the results for stellar radii of our EoSs have been possible while obtaining, within the same models, a realistic reproduction of the properties of atomic nuclei and of several other constraints. It seems unlikely that one may be able to account for significantly smaller neutron star radii in the theory considered here without abandoning the physical region of parameters. Hence, a discovery of even smaller stellar radii could provide evidence in favour of a phase transition to other degrees of freedom in neutron star interiors (Dexheimer, Negreiros, & Schramm Reference Dexheimer, Negreiros and Schramm2015).
5 IMPACT OF UNCERTAINTIES IN THE HYPERON COUPLINGS
We next discuss the determination of the values of the hyperon couplings in our FSU2H EoS and estimate the influence that the uncertainties in these couplings may have on the predictions for neutron star masses and radii.
We recall that the potential felt by a hyperon i in j-particle matter is given by
in our model, where
![]() $\bar{\sigma }^{(j)}$
,
$\bar{\sigma }^{(j)}$
,
![]() $\bar{\omega }^{(j)}$
,
$\bar{\omega }^{(j)}$
,
![]() $\bar{\rho }^{(j)}$
, and
$\bar{\rho }^{(j)}$
, and
![]() $\bar{\phi }^{(j)}$
are the meson field values in j-particle matter while I
3i
denotes the third component of the isospin operator. Flavour SU(3) symmetry, the vector dominance model, and ideal mixing for the physical ω and ϕ mesons, permit relating the couplings between the hyperons and the vector mesons to the nucleon couplings g
ωN
and g
ρN
(Schaffner & Mishustin Reference Schaffner and Mishustin1996; Banik, Hempel, & Bandyopadhyay Reference Banik, Hempel and Bandyopadhyay2014; Miyatsu, Yamamuro, & Nakazato Reference Miyatsu, Yamamuro and Nakazato2013; Weissenborn, Chatterjee, & Schaffner-Bielich Reference Weissenborn, Chatterjee and Schaffner-Bielich2012; Colucci & Sedrakian Reference Colucci and Sedrakian2013; Tolos et al. Reference Tolos, Centelles and Ramos2017), according to the ratios
$\bar{\phi }^{(j)}$
are the meson field values in j-particle matter while I
3i
denotes the third component of the isospin operator. Flavour SU(3) symmetry, the vector dominance model, and ideal mixing for the physical ω and ϕ mesons, permit relating the couplings between the hyperons and the vector mesons to the nucleon couplings g
ωN
and g
ρN
(Schaffner & Mishustin Reference Schaffner and Mishustin1996; Banik, Hempel, & Bandyopadhyay Reference Banik, Hempel and Bandyopadhyay2014; Miyatsu, Yamamuro, & Nakazato Reference Miyatsu, Yamamuro and Nakazato2013; Weissenborn, Chatterjee, & Schaffner-Bielich Reference Weissenborn, Chatterjee and Schaffner-Bielich2012; Colucci & Sedrakian Reference Colucci and Sedrakian2013; Tolos et al. Reference Tolos, Centelles and Ramos2017), according to the ratios
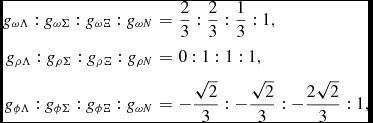 $$\begin{eqnarray}
g_{\omega \Lambda }:g_{\omega \Sigma }:g_{\omega \Xi }:g_{\omega N}&=&\frac{2}{3}:\frac{2}{3}:\frac{1}{3}:1, \nonumber \\
g_{\rho \Lambda }:g_{\rho \Sigma }:g_{\rho \Xi }:g_{\rho N}&=&0:1:1:1, \nonumber \\
g_{\phi \Lambda }: g_{\phi \Sigma }: g_{\phi \Xi }:g_{\omega N}&=& -\frac{\sqrt{2}}{3}: -\frac{\sqrt{2}}{3}: -\frac{2\sqrt{2}}{3}: 1 , \ \ \ \ \ \ \
\end{eqnarray}$$
$$\begin{eqnarray}
g_{\omega \Lambda }:g_{\omega \Sigma }:g_{\omega \Xi }:g_{\omega N}&=&\frac{2}{3}:\frac{2}{3}:\frac{1}{3}:1, \nonumber \\
g_{\rho \Lambda }:g_{\rho \Sigma }:g_{\rho \Xi }:g_{\rho N}&=&0:1:1:1, \nonumber \\
g_{\phi \Lambda }: g_{\phi \Sigma }: g_{\phi \Xi }:g_{\omega N}&=& -\frac{\sqrt{2}}{3}: -\frac{\sqrt{2}}{3}: -\frac{2\sqrt{2}}{3}: 1 , \ \ \ \ \ \ \
\end{eqnarray}$$
and noting that g
ϕN
= 0. We reduce by 20% the coupling of the Λ hyperon to the ϕ meson in order to obtain a ΛΛ bond energy in Λ matter at a density
![]() $n_\Lambda \simeq n_0/5$
of ΔB
ΛΛ(n
0/5) = 0.67 MeV, thereby reproducing the value extracted from the 6
ΛΛHe double Λ hypernucleus, also known as the Nagara event (Takahashi et al. Reference Takahashi2001; Ahn et al. Reference Ahn2013).
$n_\Lambda \simeq n_0/5$
of ΔB
ΛΛ(n
0/5) = 0.67 MeV, thereby reproducing the value extracted from the 6
ΛΛHe double Λ hypernucleus, also known as the Nagara event (Takahashi et al. Reference Takahashi2001; Ahn et al. Reference Ahn2013).
The coupling of each hyperon to the scalar σ meson field is left as a free parameter to be adjusted to reproduce the hyperon potential in SNM, derived from hypernuclear data. It is well known that a Woods–Saxon type potential of depth
![]() $U_\Lambda ^{(N)}(n_0) \sim -28$
MeV reproduces the bulk of Λ hypernuclei binding energies (Millener, Dover, & Gal Reference Millener, Dover and Gal1988). As for the Σ hyperon, a moderate repulsive potential could be extracted from analyses of (π−, K
+) reactions off nuclei (Noumi et al. Reference Noumi2002) done in Harada & Hirabayashi (Reference Harada and Hirabayashi2006) and Kohno et al. (Reference Kohno, Fujiwara, Watanabe, Ogata and Kawai2006). Fits to Σ− atomic data (Friedman & Gal Reference Friedman and Gal2007) also point towards a transition from an attractive Σ-nucleus potential at the surface to a repulsive one inside the nucleus, the size of the repulsion not being well determined. The potential felt by a Ξ hyperon in SNM is also quite uncertain. Old emulsion data indicate sizable attractive values of around
$U_\Lambda ^{(N)}(n_0) \sim -28$
MeV reproduces the bulk of Λ hypernuclei binding energies (Millener, Dover, & Gal Reference Millener, Dover and Gal1988). As for the Σ hyperon, a moderate repulsive potential could be extracted from analyses of (π−, K
+) reactions off nuclei (Noumi et al. Reference Noumi2002) done in Harada & Hirabayashi (Reference Harada and Hirabayashi2006) and Kohno et al. (Reference Kohno, Fujiwara, Watanabe, Ogata and Kawai2006). Fits to Σ− atomic data (Friedman & Gal Reference Friedman and Gal2007) also point towards a transition from an attractive Σ-nucleus potential at the surface to a repulsive one inside the nucleus, the size of the repulsion not being well determined. The potential felt by a Ξ hyperon in SNM is also quite uncertain. Old emulsion data indicate sizable attractive values of around
![]() $U_\Xi ^{(N)}(n_0) = - 24 \pm 4$
MeV (Dover & Gal Reference Dover and Gal1983), while the analyses of the (K
−, K
+) reaction on a 12C target suggest a milder attraction (Fukuda et al. Reference Fukuda1998; Khaustov et al. Reference Khaustov2000). Taking these experimental uncertainties into account, we allow the hyperon potentials in SNM to take the following range of values:
$U_\Xi ^{(N)}(n_0) = - 24 \pm 4$
MeV (Dover & Gal Reference Dover and Gal1983), while the analyses of the (K
−, K
+) reaction on a 12C target suggest a milder attraction (Fukuda et al. Reference Fukuda1998; Khaustov et al. Reference Khaustov2000). Taking these experimental uncertainties into account, we allow the hyperon potentials in SNM to take the following range of values:
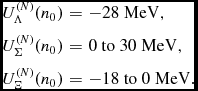 $$\begin{eqnarray}
U_{\Lambda }^{(N)}(n_0)&=&-28~{\rm MeV}, \nonumber \\
U_{\Sigma }^{(N)}(n_0)&=&0~{\rm to}~ 30~{\rm MeV}, \nonumber \\
U_{\Xi }^{(N)}(n_0)&=&-18~{\rm to}~0~{\rm MeV}.
\end{eqnarray}$$
$$\begin{eqnarray}
U_{\Lambda }^{(N)}(n_0)&=&-28~{\rm MeV}, \nonumber \\
U_{\Sigma }^{(N)}(n_0)&=&0~{\rm to}~ 30~{\rm MeV}, \nonumber \\
U_{\Xi }^{(N)}(n_0)&=&-18~{\rm to}~0~{\rm MeV}.
\end{eqnarray}$$
Note that we only consider uncertainties for the Σ and Ξ potentials, given the consensus on the Λ potential at saturation. The range of values for the hyperon potentials in SNM give rise to the following range for the hyperon-σ couplings:
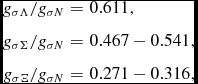 $$\begin{eqnarray}
g_{\sigma \Lambda }/g_{\sigma N}&=& 0.611, \nonumber \\
g_{\sigma \Sigma }/g_{\sigma N}&=& 0.467 - 0.541, \nonumber \\
g_{\sigma \Xi }/g_{\sigma N} &=& 0.271 - 0.316,
\end{eqnarray}$$
$$\begin{eqnarray}
g_{\sigma \Lambda }/g_{\sigma N}&=& 0.611, \nonumber \\
g_{\sigma \Sigma }/g_{\sigma N}&=& 0.467 - 0.541, \nonumber \\
g_{\sigma \Xi }/g_{\sigma N} &=& 0.271 - 0.316,
\end{eqnarray}$$
where the lower values correspond to the most repulsive situation [
![]() $U_\Sigma ^{(N)}(n_0) =30$
MeV,
$U_\Sigma ^{(N)}(n_0) =30$
MeV,
![]() $U_\Xi ^{(N)}(n_0)=0$
MeV] and the upper ones to the most attractive one (
$U_\Xi ^{(N)}(n_0)=0$
MeV] and the upper ones to the most attractive one (
![]() $U_\Sigma ^{(N)}(n_0) =0$
MeV,
$U_\Sigma ^{(N)}(n_0) =0$
MeV,
![]() $U_\Xi ^{(N)}(n_0)=-18$
MeV). In our baseline FSU2H model used in the calculations of Section 4, we have adopted the values U
(N)
Λ(n
0) = −28 MeV,
$U_\Xi ^{(N)}(n_0)=-18$
MeV). In our baseline FSU2H model used in the calculations of Section 4, we have adopted the values U
(N)
Λ(n
0) = −28 MeV,
![]() $U_\Sigma ^{(N)}(n_0) = 30$
MeV, and
$U_\Sigma ^{(N)}(n_0) = 30$
MeV, and
![]() $U_\Xi ^{(N)}(n_0)= -18$
MeV, which lead to the couplings g
σΛ = 0.611g
σN
, g
σΣ = 0.467g
σN
, and g
σΞ = 0.316g
σN
.
$U_\Xi ^{(N)}(n_0)= -18$
MeV, which lead to the couplings g
σΛ = 0.611g
σN
, g
σΣ = 0.467g
σN
, and g
σΞ = 0.316g
σN
.
The hyperon potentials are shown, as functions of the nuclear density, in Figure 3. The left panel shows the potentials for isospin SNM, while the right panel corresponds to PNM, which is closer to the conditions of beta stable neutron star matter, where differences between the potentials for the different members of the same isospin multiplet can be seen. In order not to overcrowd the figure, we have omitted the potentials of the positively charged hyperons, as they do not appear in the beta stable neutron star matter configurations appropriate for the present study. The coloured bands enclose the dispersion of results obtained employing the hyperon-σ coupling ranges displayed in Equation (17). The range of couplings has been determined from the uncertainties of the hypernuclear data and, strictly speaking, corresponds to normal nuclear matter density, n 0. However, the coupling constants are density independent in our model and we can then obtain a range of values for the potential at any density. Specially important are the potentials around 2n 0 and beyond, which is the region of densities where hyperons are present in the models explored here (Tolos et al. Reference Tolos, Centelles and Ramos2017). As can be seen from the figure, the range of values for the hyperon potentials at 2n 0 in PNM are the following: U (N) Λ(2n 0) = 4 MeV, U (N) Σ− (2n 0) = 84~to~130 MeV, U (N) Σ0 (2n 0) = 47~to~93 MeV, U (N) Ξ− (2n 0) = 14~to~42 MeV, and U (N) Ξ0 (2n 0) = −22 to ~5 MeV. We note that this range of values will strongly affect the composition of the neutron star, as we will show at the end of this section.

Figure 3. Hyperon single-particle potentials of our RMF models, as functions of the nuclear density, in the case of isospin SNM (left panel) and PNM (right panel). The bands result from varying the hyperon-σ couplings within the values given in Equation (17) to account for the experimental uncertainties of the hyperon potentials derived from hypernuclear data.
In Figure 4, we show the M–R relation for neutron stars obtained with the FSU2H model. The band collects the results obtained varying the hyperon couplings to the σ meson within the ranges in Equation (17), which produce maximum masses that differ by at most 0.1M⊙. This is a small effect, as it is obvious that the hyperon potentials at nuclear densities of around 6n 0 in the centre of 2M⊙ stars (see Table 3) suffer a much larger uncertainty than the one we extrapolated from the normal nuclear densities characteristic of hypernuclear data. Indeed, the uncertainties tied to our lack of knowledge of the hyperon–nucleon and hyperon–hyperon interactions around the hyperon onset density of ~2n 0 and beyond have often been exploited to build up RMF models that produce hyperonic neutron stars with maximum masses larger than 2M⊙ (Weissenborn et al. Reference Weissenborn, Chatterjee and Schaffner-Bielich2012; Bednarek et al. Reference Bednarek, Haensel, Zdunik, Bejger and Manka2012; van Dalen, Colucci, & Sedrakian Reference van Dalen, Colucci and Sedrakian2014; Oertel et al. Reference Oertel, Providencia, Gulminelli and Raduta2015; Fortin et al. Reference Fortin, Avancini, Providncia and Vidaa2017). As can be seen in the extensive analyses of various models in Fortin et al. (Reference Fortin, Zdunik, Haensel and Bejger2015), the maximum masses turn out to be within a 0.3M⊙ band. It is therefore clear that determining the hyperon interactions at higher densities, as could be done from the analysis of HIC experiments (Morita, Furumoto, & Ohnishi Reference Morita, Furumoto and Ohnishi2015), would help constraining the models in the appropriate regimes found in neutron stars.

Figure 4. Mass versus radius for neutron stars from the FSU2H model. The band results from varying the hyperon-σ couplings within the values given in Equation (17) to account for the experimental uncertainties of the hyperon potentials derived from hypernuclear data.
Let us finish this section by showing, in Figure 5, the particle fractions as functions of the baryonic density, for the FSU2H model (lower panel), where the coloured bands are obtained for the range of hyperon-σ couplings employed in this work. For completeness, we also show the particle fractions for the nucleonic FSU2R model in the upper panel, where we can see that the absence of negatively charged hyperons maintains a constant population of electrons and muons, and hence of protons and neutrons, already from slightly above 2n 0. As for the FSU2H model, we note that all the particle fractions are affected by the hypernuclear data uncertainties, even if these are encoded only in the Σ and Ξ couplings to the σ meson. Upon inspecting the range of densities where hyperons may be present, we see that, although one can generally conclude that hyperons appear around 2n 0, the order of appearance of each species is not determined, owing to the uncertainties derived from hypernuclear data. The first hyperon to appear can be either a Λ or a Σ−, the latter case only in the less repulsive situation allowed by data, namely when U (N) Σ(n 0) ≃ 0 MeV. In fact, when the Σ feels its most repulsive potential value, it can even appear after the Ξ− hyperon. This happens when the Ξ potential value is on the most attractive side of the allowed region, namely U (N) Σ(n 0) = −18 MeV. However, if one decreases the amount of attraction, as data permits, the Ξ− onset density is rapidly pushed towards larger values, even beyond the maximum density of 6n 0 represented in the figure, which stands as a representative central density of hyperonic stars. Summarising, although hyperons are present in the interior of neutron stars modelled by the FSU2H interaction, the lack of precise knowledge on the hyperon–nuclear interactions prevents one from establishing the specific hyperonic composition in the interior of the star.

Figure 5. Particle fractions as functions of the baryonic density for the nucleonic FSU2R model (upper panel) and the hyperonic FSU2H model (lower panel). The bands in the lower panel result from varying the hyperon-σ couplings within the values given in Equation (17) to account for the experimental uncertainties of the hyperon potentials derived from hypernuclear data. The coloured lines guide the eye to help distinguishing each case properly in the regions of overlapping bands.
6 SUMMARY
We have reinvestigated our previous results on the EoS for the nucleonic and hyperonic inner core of neutron stars (Tolos et al. Reference Tolos, Centelles and Ramos2017), that fullfil the 2 M⊙ observations (Demorest et al. Reference Demorest, Pennucci, Ransom, Roberts and Hessels2010; Antoniadis et al. Reference Antoniadis2013) and the recent determinations of radii below 13-km region (Guillot et al. Reference Guillot, Servillat, Webb and Rutledge2013; Lattimer & Steiner Reference Lattimer and Steiner2014a; Heinke et al. Reference Heinke2014; Guillot & Rutledge Reference Guillot and Rutledge2014; Ozel et al. Reference Ozel, Psaltis, Guver, Baym, Heinke and Guillot2016; Lattimer & Prakash Reference Lattimer and Prakash2016), as well as the saturation properties of nuclear matter and finite nuclei (Tsang et al. Reference Tsang2012; Chen & Piekarewicz Reference Chen and Piekarewicz2014) and the constraints extracted from HICs (Danielewicz et al. Reference Danielewicz, Lacey and Lynch2002; Fuchs et al. Reference Fuchs, Faessler, Zabrodin and Zheng2001; Lynch et al. Reference Lynch, Tsang, Zhang, Danielewicz, Famiano, Li and Steiner2009). The two models formulated in Tolos et al. (Reference Tolos, Centelles and Ramos2017), the FSU2R (with nucleons) and FSU2H (with nucleons and hyperons) models, have been updated by improving the behaviour of PNM at subsaturation densities. Above saturation density, the updated models and those of Tolos et al. (Reference Tolos, Centelles and Ramos2017) are very similar.
Using these updated interactions, we have obtained values for the PNM pressure at saturation density of 2.44 MeV fm−3 in FSU2R and of 2.30 MeV fm−3 in FSU2H, that are consistent with the estimates from chiral forces (Fortin et al. Reference Fortin, Zdunik, Haensel and Bejger2015; Hagen et al. Reference Hagen2015). The symmetry energy and its slope at saturation become E sym(n 0) = 30.7 MeV and L = 46.9 MeV in FSU2R and E sym(n 0) = 30.5 MeV and L = 44.5 MeV in FSU2H, thus being in good agreement with several recent estimates based on terrestrial experiments, different astrophysical observations, and theoretical calculations (Li & Han Reference Li and Han2013; Lattimer & Lim Reference Lattimer and Lim2013; Roca-Maza et al. Reference Roca-Maza, Viñas, Centelles, Agrawal, Colo’, Paar, Piekarewicz and Vretenar2015; Hagen et al. Reference Hagen2015; Oertel et al. Reference Oertel, Hempel, Klähn and Typel2017; Birkhan et al. Reference Birkhan2017). Furthermore, the reviewed FSU2R and FSU2H models predict a neutron skin thickness of 0.15 fm in 208Pb and of 0.166 fm in 48Ca, which turn out to be compatible with previous experimental and theoretical determinations (Roca-Maza et al. Reference Roca-Maza, Viñas, Centelles, Agrawal, Colo’, Paar, Piekarewicz and Vretenar2015; Tarbert et al. Reference Tarbert2014; Abrahamyan et al. Reference Abrahamyan2012; Horowitz et al. Reference Horowitz2012; Hagen et al. Reference Hagen2015; Birkhan et al. Reference Birkhan2017).
With regards to the mass and radius of neutron stars, radii below 13 km can be achieved because of the softening of the symmetry energy around saturation density whereas, at the same time, 2M⊙ stars can be obtained as the pressure of the high-density EoS is hard enough. These results are not drastically changed when using the updated FSU2R and FSU2H interactions as compared to the previous versions in ref. Tolos et al. (Reference Tolos, Centelles and Ramos2017), because of the similar EoSs produced above saturation density. The numerical tabulations of the EoS and of the M–R relation from the models FSU2R (npeμ matter) and FSU2H (npYeμ matter) as a function of the number density n/n 0 are shown in Tables A1 and A2 for completeness.
However, the mass and composition of neutron stars might be strongly affected due to the uncertainties of the hyperon–nucleon couplings. The values of the hyperon couplings are determined from SU(3) flavour symmetry and from the available experimental information on hypernuclei, in particular, by fitting to the optical potential of hyperons extracted from the data. The coupling of each hyperon to the σ meson field is left as a free parameter to be adjusted to reproduce the hyperon potential in SNM within the experimental uncertainties. As a result, we have found that the onset of appearance of the different hyperons strongly depends on the hyperon–nuclear uncertainties, whereas the maximum masses differ by at most 0.1M⊙, thus being less sensitive to the changes on the hyperon–nucleon couplings. This latter conclusion has to be taken with care, though, since the hyperon potentials at densities in the centre of 2M⊙ stars suffer much larger uncertainties than the ones we have extrapolated from hypernuclear data at saturation. Hence, a greater dispersion of values for the maximum mass might be expected. The progress in the characterisation of hyperon–nucleon interactions in dense matter derived from chiral effective forces (Haidenbauer et al. Reference Haidenbauer, Meißner, Kaiser and Weise2017), on the theoretical front, and from studies of HICs (Morita et al. Reference Morita, Furumoto and Ohnishi2015), on the experimental front, should contribute greatly to narrow down these uncertainties.
ACKNOWLEDGEMENTS
L.T. acknowledges support from the Ramón y Cajal research programme, FPA2013-43425-P and FPA2016-81114-P Grants from Ministerio de Economia y Competitividad (MINECO) and NewCompstar COST Action MP1304. M.C. and A.R. acknowledge support from Grant No. FIS2014-54672-P from MINECO, Grant No. 2014SGR-401 from Generalitat de Catalunya, and the project MDM-2014-0369 of ICCUB (Unidad de Excelencia María de Maeztu) from MINECO. L.T. and A.R. acknowledge support from the Spanish Excellence Network on Hadronic Physics FIS2014-57026-REDT from MINECO.
APPENDIX
For ease of use, in this appendix, we provide in tabular form the results for the EoS and the M–R relation calculated with the FSU2R and FSU2H models discussed in the text.
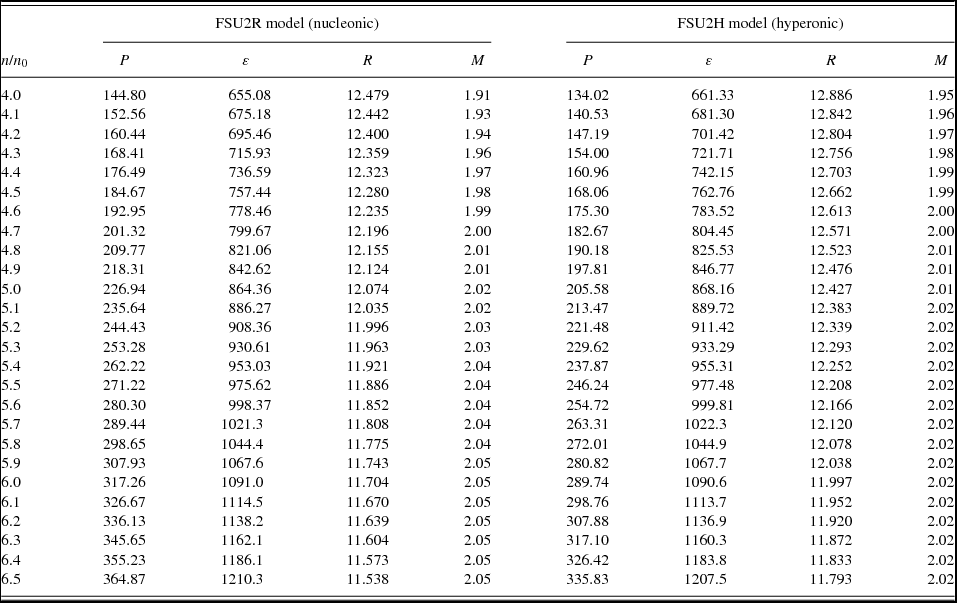
Table A1. Numerical data of the EoS for the core of neutron stars and of the M–R relation from the models FSU2R (npeμ matter) and FSU2H (npYeμ matter), as a function of the number density n/n 0 (with n 0 = 0.1505 fm−3, cf. Table 2). The pressure P and mass–energy density ε are in MeV fm−3, while the neutron star radius R and mass M are in km and M⊙ units, respectively.
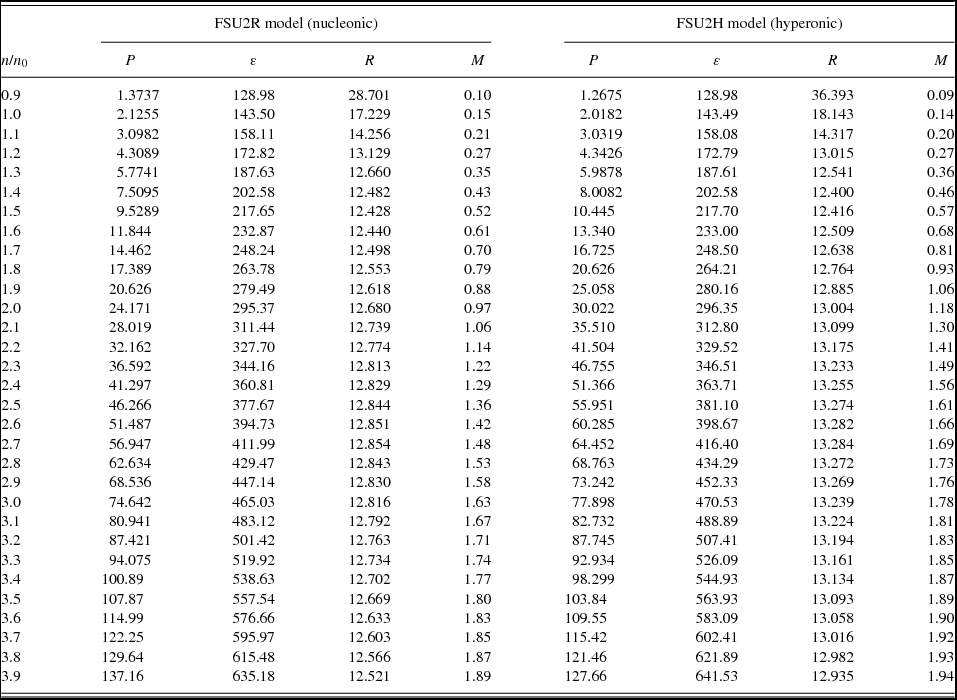
Table A2. Continuation of Table A1.