Published online by Cambridge University Press: 17 April 2018
Let p ≥ 3 be a prime. A generalized multi-edge spinal group
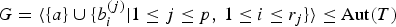 $$G = \langle \{ a\} \cup \{ b_i^{(j)} {\rm \mid }1 \le j \le p,\, 1 \le i \le r_j\} \rangle \le {\rm Aut}(T)$$
$$G = \langle \{ a\} \cup \{ b_i^{(j)} {\rm \mid }1 \le j \le p,\, 1 \le i \le r_j\} \rangle \le {\rm Aut}(T)$$ $b^{(j)}_{1}, \ldots, b^{(j)}_{r_{j}}$ of directed automorphisms, each family sharing a common directed path disjoint from the paths of the other families. This notion generalizes the concepts of multi-edge spinal groups, including the widely studied GGS groups (named after Grigorchuk, Gupta and Sidki), and extended Gupta–Sidki groups that were introduced by Pervova [‘Profinite completions of some groups acting on trees, J. Algebra310 (2007), 858–879’]. Extending techniques that were developed in these more special cases, we prove: generalized multi-edge spinal groups that are torsion have no maximal subgroups of infinite index. Furthermore, we use tree enveloping algebras, which were introduced by Sidki [‘A primitive ring associated to a Burnside 3-group, J. London Math. Soc.55 (1997), 55–64’] and Bartholdi [‘Branch rings, thinned rings, tree enveloping rings, Israel J. Math.154 (2006), 93–139’], to show that certain generalized multi-edge spinal groups admit faithful infinite-dimensional irreducible representations over the prime field ℤ/pℤ.
$b^{(j)}_{1}, \ldots, b^{(j)}_{r_{j}}$ of directed automorphisms, each family sharing a common directed path disjoint from the paths of the other families. This notion generalizes the concepts of multi-edge spinal groups, including the widely studied GGS groups (named after Grigorchuk, Gupta and Sidki), and extended Gupta–Sidki groups that were introduced by Pervova [‘Profinite completions of some groups acting on trees, J. Algebra310 (2007), 858–879’]. Extending techniques that were developed in these more special cases, we prove: generalized multi-edge spinal groups that are torsion have no maximal subgroups of infinite index. Furthermore, we use tree enveloping algebras, which were introduced by Sidki [‘A primitive ring associated to a Burnside 3-group, J. London Math. Soc.55 (1997), 55–64’] and Bartholdi [‘Branch rings, thinned rings, tree enveloping rings, Israel J. Math.154 (2006), 93–139’], to show that certain generalized multi-edge spinal groups admit faithful infinite-dimensional irreducible representations over the prime field ℤ/pℤ.