Introduction
Knowledge about the thermal state of the crust is important when aiming for a thorough reconstruction of the geological history of a region, and also when calculating maturation of hydrocarbon source rocks or for successful geothermal prospecting. Data from boreholes provide a useful but local estimate of subsurface temperatures and the thermal state of the shallow crust, and are often used as constraints when estimating heat flow (e.g. Agemar et al., Reference Agemar, Schellschmidt and Schulz2012; Bonté et al., Reference Bonté, Van Wees and Verweij2012) or lithospheric strength (e.g. Tesauro et al., Reference Tesauro, Kaban, Cloetingh, Hardebol and Beekman2007) at deeper levels.
Changes in the surface temperature affect the temperature at depth. The magnitude, duration and penetration depth of this effect depend on the amplitude and especially the wavelength of the variations in the surface temperature. For glacial–interglacial cycles of several hundreds of thousands of years, the penetration depth of the detectable effect extends to a few kilometres (Pollack & Huang, Reference Pollack and Huang2000; Bodri & Cermak, Reference Bodri and Cermak2007; Huang et al., Reference Huang, Pollack and Shen2008; Majorowicz & Šafanda, Reference Majorowicz and Šafanda2008; Kukkonen et al., Reference Kukkonen, Rath, Kivekäs, Šafanda and Čermak2011; Majorowicz & Wybraniec, Reference Majorowicz and Wybraniec2011). The influence of these paleoclimatic variations is often neglected when heat flow at deeper crustal or lithospheric levels is estimated from temperature measurements in the shallow crust. However, the inclusion of surface temperature variations on the timescale of glacial–interglacial cycles yields heatflow corrections up to 20 mW/m2 in Europe (e.g. Majorowicz & Šafanda, Reference Majorowicz and Šafanda2008; Majorowicz & Wybraniec, Reference Majorowicz and Wybraniec2011), underlining the fact that the thermal state of the crust is a transient phenomenon.
The average present-day thermal gradient in the Netherlands is around 20°C km–1 in the shallow subsurface (i.e. ∼70–500 m) (van Dalfsen, Reference van Dalfsen1981; Bense & Kooi, Reference Bense and Kooi2004; Karg et al., Reference Karg, Bücker and Schellschmidt2004; Kooi, Reference Kooi2008), whereas at larger depths (500 m to 3 km) it is between 30 and 35°C km–1 (e.g. Ramaekers, Reference Ramaeckers, Hurtig, Cermak, Haenel and Zui1991; van Balen et al., Reference van Balen, van Bergen, de Leeuw, Pagnier, Simmelink, van Wees and Verweij2000, Reference van Balen, Verweij, van Wees, Simmelink, van Bergen and Pagnier2002; Luijendijk et al., Reference Luijendijk, ter Voorde, van Balen, Verweij and Simmelink2011; Bonté et al. Reference Bonté, Van Wees and Verweij2012). This is a regional phenomenon, which may also imply that in the Netherlands the thermal field is in a transient state of heating as a response to the increase in surface temperature since the last glacial maximum: at the end of the Weichselien (∼18 kya), yearly average surface temperatures were below –5°C.
In addition to crustal heat flow studies, borehole temperature data have been used extensively to reconstruct ground surface temperature history as a proxy for climate change. Long-term studies (i.e. up to 100 kyrs) have been carried out by, for example, Kukkonen & Šafanda (Reference Kukkonen and Šafanda1996), Kukkonen et al. (Reference Kukkonen, Gosnold and Šafanda1998), Šafanda & Rajver (Reference Šafanda and Rajver2001), Kukkonen & Jõeleht (Reference Kukkonen and Jõeleht2003), Šafanda et al. (Reference Šafanda, Szewczyk and Majorowicz2004) and Kukkonen et al. (Reference Kukkonen, Rath, Kivekäs, Šafanda and Čermak2011). These studies were mostly based on one or two boreholes and all focused on the Baltic Shield and the East European Platform. Data from boreholes capturing periods up to 1000 years ago have been used to make surface temperature reconstructions averaged over wider regions, especially in the Northern Hemisphere (e.g. Pollack et al. Reference Pollack, Huang and Shen1998; Harris & Chapman, Reference Harris and Chapman2005).
Deltaic areas like the Netherlands have always been avoided in studies on paleoclimatic signals in subsurface temperatures because of disturbing effects of shallow processes like groundwater flow and land use (e.g. Kooi, Reference Kooi2008). The Netherlands are exceptional, however, in the sense that a very large amount of data is available in which these local effects can be largely suppressed. Although this average geotherm is not sufficiently detailed to make a reconstruction of the paleo-climate from the subsurface geotherm, it allows for the investigation of whether the decrease in thermal gradient that appears in the average geotherm beneath the Netherlands is in concert with the estimated paleoclimatic signal as derived from climate proxy data.
Here we analyse the effect of changes in surface temperatures on timescales of hundreds of kyrs on the geothermal gradient in the Netherlands, both in time and as a function of depth, using a numerical model that calculates heat transfer through the crust. We compare our findings to published heat-flow data for the Netherlands.
The model
We used an implicit finite difference model that calculates changes in temperature in the crust due to conduction. The model solves the heat equation:
where T is temperature (°C), t is time (s), κ is thermal diffusivity (m2 s–1), A is heat production (W m–3), ρ is density (kg m–3) and C is specific heat (J °C–1 kg–1).
Here the thermal properties are regarded as bulk properties of the crust, i.e. of rock matrix and pore fluids together. Boundary conditions are a prescribed temperature that can change with time at the surface and a constant temperature at the base of the model (base lithosphere). The start condition of the model is a steady-state geotherm resulting from the initial boundary conditions. Starting from this steady-state situation we change the surface temperature to observe the effects on the geotherm in depth and time.
Comparison with analytical solutions: the influence of Milankovitch cycles
The magnitude, duration and penetration depth of the effect of changes in the surface temperature depend on its amplitude and especially the wavelength of the temperature variations. The analytical solution for a sinusoidal variation in surface temperature, for the case without spatial variations in the thermal conductivity and in the absence of heat production, is (e.g. Furbish, Reference Furbish1997):
where T is temperature (°C), t is time (s), z is depth (m), λ is the period of the temperature signal (s), T a is the amplitude of the temperature change at the surface (°C) and κ is thermal diffusivity (m2s–1).
Using this equation we can compare the effects of the three major climatic (Milankovitch) cycles, with periods of 23, 42 and 100 kyr (e.g. Hays et al., Reference Hays, Imbrie and Shackleton1976). The equation shows that:
(a) The decrease in the amplitude of the temperature variation with depth is larger when the frequency of the temperature cycle is higher: in that case the temperature at depth has less time to adapt to the changes. As can be calculated from eqn 2, when assuming a thermal diffusivity κ of 10–6 m2s–1, the amplitude reduces by 63% every kilometre for the 100 kyr cycle, whereas for the 42 kyr cycle the amplitude reduction is 79% per kilometre and for the 23 kyr cycle it is 88% per kilometre.
(b) There is a phase change between the variation in surface temperature and the variations at depth. For the 100 kyr cycle, the response has a delay of 15.9 kyr per kilometre extra depth. At a depth of 3.1 km, the oscillation has thus been reversed, implying that a minimum surface temperature coincides with a maximum temperature at a depth of 3.1 km and vice versa. For the 42 kyr cycle, the delay of the response is 10.3 kyr per kilometre extra depth and the reversal is at a depth of 2 km, and for the 23 kyr cycle, the phase delay is 7.6 kyr km–1 and the reversal occurs already at a depth of 1.5 km.
These findings are in accordance with the numerical solutions for these cyclic surface temperature changes, which are depicted for the 23 kyr and 42 kyr period in Fig. 1. In addition, Fig. 2 shows both the modelling result and the analytical solution in one graph for a surface temperature signal with a scaled amplitude of 1, a thermal diffusivity κ of 10–6 m2s–1 and a period of 100 kyr.

Fig. 1. The relative response to cyclic surface temperature variations (a) with a period of 23 kyr and (b) with a period of 42 kyr. The amplitudes of the cycles are scaled to 1.

Fig. 2. The relative response to cyclic surface temperature variations with a period of 100 kyr and an amplitude scaled to 1, calculated both analytically and numerically.
Ultimately, the combination of the reduction in amplitude and the delay of the phase of the oscillation with depth results in variations in the thermal gradient (Fig. 3). The figure shows that the shallow thermal gradient is reduced when the surface temperature is increasing, and rises when the surface temperature is decreasing. When the surface temperature is at its minimum, the shallow gradient is at its maximum, and vice versa. Moreover, as demonstrated by Fig. 3, the geotherm does not reach its steady-state configuration at any moment during the oscillations, indicating that a transient temperature field is not an exception but the rule.

Fig. 3. The downward propagation of changes in surface temperature, with a dimensionless (scaled) amplitude of 1 and periods of 100 kyr (upper panels), 42 kyr (central panels) and 23 kyr (lower panels), separated in phases of increasing surface temperature (left panels) and decreasing surface temperatures (right panels). Dark blue, red, green, purple and light blue curves represent successive moments, with time steps of 10 kyr (for the 100 kyr cyle), 4.2 kyr (for the 42 kyr cycle) or 2.3 kyr (for the 23 kyr cycle).
In reality, Milankovich cycles act simultaneously, causing the thermal phases to offset or amplify each other. Furthermore, other processes also have an influence on the climate, therefore, in order to investigate the effect of the climate on the subsurface temperature in the Netherlands, we used climate reconstructions which were available for up to 130 kya, and we tested the effect of several end member scenarios for the surface temperature history before 130 kya.
The thermal state of the Netherlands: variations with depth
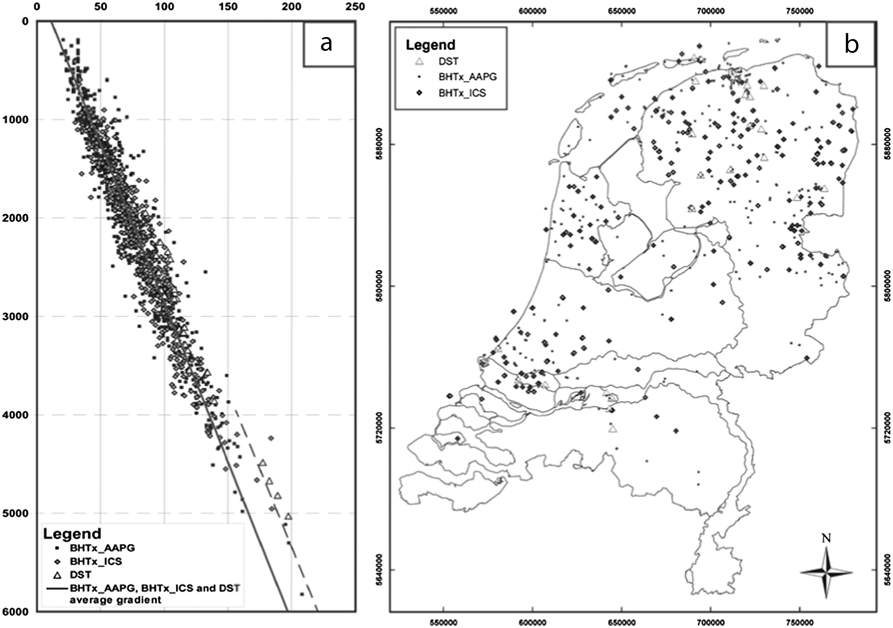
The average geothermal gradient in the Netherlands at the depth interval from 0.5 to 3 km is between 31 and 33°C km–1 (Ramaekers, Reference Ramaeckers, Hurtig, Cermak, Haenel and Zui1991). Regional values have been established, for example for the Roer Valley Graben, where the temperatures at depths of 2500 m below the surface range around an average of 98°C, implying an average geothermal gradient of 35°C km–1 up to this depth (Luijendijk et al., Reference Luijendijk, ter Voorde, van Balen, Verweij and Simmelink2011, Fig. 4), and for the West Netherlands Basin, where numerical modelling based on well data resulted in average geothermal gradients of 30± 2°C km–1 in the upper 5 km of this region (van Balen et al., Reference van Balen, van Bergen, de Leeuw, Pagnier, Simmelink, van Wees and Verweij2000). The most recent analysis of the temperature of the entire onshore Dutch underground, based on a dataset of 1241 measurements in 437 wells, yielded an average thermal gradient of 31.3°C km–1 (Bonté et al. Reference Bonté, Van Wees and Verweij2012, Fig. 5), combined with a surface temperature of 10°C (Bonté et al., Reference Bonté, Van Wees and Verweij2012; see also van Dalfsen, Reference van Dalfsen1983). Interestingly, a much lower geothermal gradient is documented in the shallow (<200 m depth) subsurface in the central part of the Netherlands (Kooi, Reference Kooi2008), in the southeastern part of the Netherlands (Bense & Kooi, Reference Bense and Kooi2004), and in the Dutch and German parts of the Lower Rhine Embayment (Karg et al., Reference Karg, Bücker and Schellschmidt2004).

Fig. 4. Compilation of temperature data and their uncertainty range in the Roer Valley Graben Area, after Luijendijk et al. (Reference Luijendijk, ter Voorde, van Balen, Verweij and Simmelink2011).

Fig. 5. Average geotherm in the Netherlands based on compilation of available borehole data, corrected for thermal perturbations by drilling (adopted from Bonté et al, Reference Bonté, Van Wees and Verweij2012). (a) Temperature as a function of depth. (b) Location of the used drillholes.
Kooi (Reference Kooi2008) compared repeated borehole temperature measurements in the central parts of the Netherlands that were recorded some three decades apart. He found gradients around 20°C km–1 to depths of about 200 m in measurements from the late 1970s. Similar gradients to depths of 400 m are common throughout the Netherlands (van Dalfsen, Reference van Dalfsen1981). In 2006, i.e. 30 years later, warming and reduced or even negative temperature gradients were observed at depths shallower than 70 m, whereas temperatures and gradients were found to be unaltered at depths larger than 70 m. The shallow subsurface warming was found to be consistent with documented increased surface air temperatures in the Netherlands since about 1980. This climate warming is too recent to have influenced temperatures at depths in excess of 70 m, explaining the relatively stable gradients of around 20°C km–1.
Below, we investigate whether the relatively low gradient of 20°C km–1 in the depth interval of 70 to 400 m, when compared to the interval from 0.5 to 3 km, can be explained by the temperature increase at the surface in the more distant past.
Input of the model
The existence of thick sediment layers in the Netherlands has a pronounced influence on its subsurface temperature structure (Bonté et al., Reference Bonté, Van Wees and Verweij2012): sediments act as an insulating layer for the crust. The sediment layering shows large spatial variations in the Netherlands, mostly due to structures and different subsidence rates. Since we use an average geotherm to constrain our models, and since our aim is to isolate the influence of the surface temperature variations from other effects, we choose to ignore this sediment blanketing effect. As shown by Bonté et al. (Reference Bonté, Van Wees and Verweij2012), this entails that the temperatures as observed in boreholes in the upper few kilometres of the subsurface can only be explained by combining an extremely low value for the thickness of the lithosphere with an unrealistic high value for the heat production in the upper crust.
The average thickness of the lithosphere beneath the Netherlands is hard to estimate due to uncertainties in composition and temperature at larger depths. Values in the literature vary from 90 km (Cloetingh et al., Reference Cloetingh, van Wees, Ziegler, Lenkey, Beekman, Tesauro, Förster, Norden, Kaban, Hardebol, Bonté, Genter, Guillou-Frottier, Ter Voorde, Sokoutis, Willingshofer, Cornu and Worum2010) to more than 150 km (Goes et al., Reference Goes, Govers and Vacher2000). In order to obtain present-day values for the geothermal gradient that are comparable with those measured in the Netherlands, we had to adopt a rather thin lithosphere of 90 km and a heat production of 3.6 μW/m3 in the upper 10 km of the crust. The resulting steady-state geotherm is shown in Fig. 6. Its gradient decreases with depth due to the effect of the heat production, from 32.2°C km–1 at the surface, via 28.7°C km–1 at a depth of 3 km, to 22.1°C km–1 at a depth of 8 km.

Fig. 6. Temperature with depth at the start of the modelling (i.e. 130 kya).
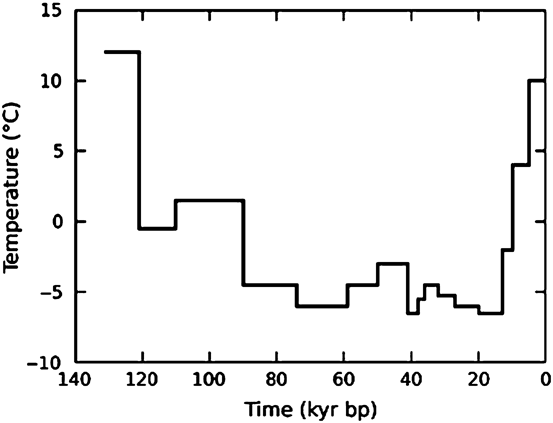
Starting from this geotherm, we have applied the surface temperature proposed by Luijendijk et al. (2011, see Fig. 7), to represent the thermal evolution in the Netherlands during the past 130 kyr. This surface temperature history was estimated from climate proxy data such as pollen, fossil beetles (Coleoptera), plant macroremains and periglacial indicators in northwest and central Europe (Zagwijn, Reference Zagwijn1996; Huijzer & Vandenberghe, Reference Huijzer and Vandenberghe1998; Caspers & Freund, Reference Caspers and Freund2001), and in the northeastern part of the Netherlands (van Gijssel, Reference van Gijssel1995).

Fig. 7. Surface temperature history used for the simulation of temperature–depth profiles by Luijendijk et al. (Reference Luijendijk, ter Voorde, van Balen, Verweij and Simmelink2011). Based on climate proxy data published by Caspers & Freund (Reference Caspers and Freund2001), Reference van GijsselVan Gijssel (1995), Huijzer & Vandenberghe (Reference Huijzer and Vandenberghe1998), and Zagwijn (Reference Zagwijn1996).
Results
Fig. 8 shows the calculated temperature evolution with time at depths of 0.5, 1.0 and 2.0 km. In Fig. 8a we started with a steady-state geotherm with a surface temperature of –6.5°C and calculated the effect of the surface heating that had occurred since 20 kya (see Fig. 7). In this model the surface gradient decreases from 32.2°C km–1 at 20 kya to 14.4°C km–1 at present.

Fig. 8. (a) Temperature as a function of time at depths of 0, 0.5, 1.0 and 2.0 km. Results for the scenario based on estimated surface temperatures in the Netherlands during the past 20 kyr. (b) Temperature as a function of time at depths of 0, 0.5, 1.0 and 2.0 km. Results for the scenario based on estimated surface temperatures in the Netherlands during the past 130 kyr.
Fig. 8b shows the thermal evolution for the entire 130 kyr period of climate changes as depicted in Fig. 7. Again, the influence of the last cooling event is still clearly visible in the calculated present-day geotherm, although the effect is damped: The present-day geotherm resulting from this model run has a surface gradient of 20.6°C km–1. Since the model started from a surface temperature of 12°C, which cooled and heated up again in a period of ∼100 kyr, a new steady state during the cold period was never reached, therefore when the surface temperature increased to its current value, the thermal field could recover much faster than in the scenario with instantaneous cooling starting from a steady-state geotherm with a low surface temperature at 20 kya.
The present-day geotherm resulting from this model run has a surface gradient of 20.6°C km–1, a gradient of 32.1°C km–1 at a depth of 3 km and a gradient of 21.9°C km–1 at a depth of 8 km. These values are comparable to the gradients found by Kooi (Reference Kooi2008) for the upper 200 m, and by Bonté et al. (Reference Bonté, Van Wees and Verweij2012) and Luijendijk et al. (Reference Luijendijk, ter Voorde, van Balen, Verweij and Simmelink2011) for the upper 3 km. Although the absolute values are dependent on the start geotherm, which is not very well known, we can conclude that the surface temperature history in the Netherlands has been able to cause a significant increase in the gradient with depth.
Our model results show that the increase in the thermal gradient with depth in the Netherlands can be explained as a remnant from the relatively cold period that lasted until 18 kya. Furthermore, it demonstrates that the thermal history before 18 kya still has a profound influence on the subsurface thermal field: the climate warming that started 18 kya interrupted a period of 100 kyr in which subsurface temperatures were generally decreasing. During that time period, the thermal field was still in the process of adapting to the change from warm surface temperatures of the Eemian to the glacial conditions of the Weichselian, without reaching equilibrium.
Going even further back in time, a simulation starting with the low surface temperature of the preceding Saalian glacial (from ∼238 to 128 kya) yields a predicted present-day surface gradient of 15.8 °C km–1, a gradient at 3 km depth of 29.6°C km–1 and a gradient at a depth of 8 km of 21.9°C km–1 (Fig. 9).

Fig. 9. Temperature as a function of time at depths of 0, 0.5, 1.0 and 2.0 km. Results for the scenario based on estimated surface temperatures in the Netherlands during the past 130 kyr, extended with a cold period before 130 kya.
Since the air temperature during the Oostermeer (∼243 to 238 kya) and the Saalien (i.e. during the last climate cycle before the Eemian) probably fluctuated between the same values as during the Eemian and Weichselien (e.g. Cheddadi et al., Reference Cheddadi, De Beaulieu, Jouzel, Andrieu-Ponel, Laurent, Reille, Raynaud and Bar-Hen2005), the scenarios depicted in Fig. 8b and in Fig. 9 can be considered as endmembers: one assuming a surface temperature of 12°C and the other surface temperature of –5°C for the entire period before 130 kya.
Our results show that the continuous change in surface temperature excludes equilibrium geothermal conditions, and also that the present-day geotherm is in a transient state, for example when we extend the modelled period to calculate the future evolution of subsurface temperatures, based on a no future climate change scenario (i.e. applying a constant surface temperature), the model predicts a further heating of the shallow subsurface (Fig. 10): the geotherm at 20 kyr from now shows a surface gradient of 28.1°C km–1.

Fig. 10. Geotherms in the upper 3 km for the scenario that started at 130 kya. The purple line is the steady-state geotherm at the start of the model run, with a surface temperature of 12°C, the blue line is the modelled present-day geotherm resulting from the surface temperature history of Luijendijk et al. (2011, see Fig. 8), with a present-day surface temperature of 10°C, and the red line is the geotherm 20 kyr from now, assuming that the surface temperature remains 10°C.
Discussion
We have shown that, in the Netherlands, the changes in the surface temperature of the past 130 kyr affected the temperature at shallow crustal depths. The magnitude of this effect decreases with depth. We found changes in temperature of up to 10°C at a depth of 1 km, but of just a few degrees centigrade (<3) at a depth of 3 km.
Other processes causing changes in the subsurface temperature field with time are (1) crustal deformation, sedimentation and erosion, (2) the variation of thermal parameters, both in time and in space, (3) groundwater flow and (4) latent heat by melting and/or freezing.
(1) As shown previously (Grasemann & Mancktelow, Reference Grasemann and Mancktelow1993; ter Voorde & Bertotti, Reference ter Voorde and Bertotti1994; Luijendijk et al., Reference Luijendijk, ter Voorde, van Balen, Verweij and Simmelink2011), temperature changes due to crustal deformation by faulting in the upper crust are only detectable at short distances (< 10 km) from the fault. The effect is dependent on the rate of faulting. For fault rates up to several millimetres per year the influence of faulting is in the same order of magnitude as the changes due to the surface temperature variations. However, when the rate of faulting is in the order of tens of millimetres per year the resulting temperature changes increase to values of > 50°C. For these cases, the influence of the surface temperature on the subsurface thermal field is insignificant compared to the effect of faulting.
(2) Dependent on the rate of sedimentation, the thermal response to sediment infill of a basin may be a decrease in temperature (due to the low temperature of the sediments) or an increase (due to their insulating effect): if the sediment conductivity is 50% lower than the basement conductivity, the turning point between cooling and heating is at a sedimentation rate of 1.8 mm/yr (ter Voorde & Bertotti, Reference ter Voorde and Bertotti1994). When sedimentation has ceased, and other parameters are constant with time, the thermal field will return to a steady-state situation in which thermal gradients are inversely proportional to the conductivity. Common variations in thermal conductivity between the basement and sediments are up to a maximum of a factor 1.5, although the presence of salt, for example, may cause larger variations. Depending on the thickness and conductivity of the sediment layer, this effect may dominate the effect of the surface temperature variations.
In the Netherlands, the influence of the sediments causes large but local variations in the subsurface temperature (Bonté et al., Reference Bonté, Van Wees and Verweij2012). For example, thick upper Carboniferous (Silesian) deposits, mainly composed of shale, have a strong insulation effect in the province Zuid-Holland, whereas evaporitic (high conductive) sediments in the Zechstein layers in the northern part of the country cause a relative warm shallow (<1 km) subsurface and lower temperatures at depths around 2 km.
(3) Groundwater flow can have a substantial effect on the subsurface temperature, even in a relatively flat region like the Netherlands: Luijendijk (Reference Luijendijk2012) showed that topography-driven groundwater flow in the Roer Valley graben, despite its relatively low relief, caused locally more than 25°C of cooling at a depth of 1.5 km. The thermal response of sediments on changes in surface temperature also depends on the direction and velocity of groundwater flow (e.g. Goto et al., Reference Goto, Yamano and Kinoshita2005).
Although these three effects are able to dominate the influence of the varying surface temperature, they are all local effects, whereas the climatic signal will cause a change in the geothermal gradient on a regional scale. Only in large scale, deep reaching systems does the groundwater flow have a regional effect on the subsurface temperature distribution. In the Netherlands, such deep groundwater movements occurred during the glacials and associated low sea levels, for example during the Elsterian and Middle Saalien glaciations (Verweij, Reference Verweij2003).
Interpretation of local borehole data can be further complicated by the fact that ground surface temperature can vary spatially over both short and large distances depending on surface conditions (e.g. vegetation, moisture availability, snow cover characteristics), which determine the local surface energy balance (e.g. Chisholm & Chapman, Reference Chisholm and Chapman1992). Although magnitudes of these variations appear to be generally less than 2°C in the Netherlands (Kooi, Reference Kooi2008), they can affect temperatures to kilometres depth and create significant variations in thermal gradients at shallow (i.e. <200 m) depth intervals.
For freezing or thawing of ice-rich permafrost, latent heating moderates the response of the subsurface temperatures to changes in surface temperature. When the surface temperature increases and thawing occurs, this will take energy, implying that temperatures at larger depth will increase less than without thawing. Where there is a decrease in surface temperature, and this is accompanied by freezing, energy is released and the decrease in subsurface temperature is reduced (see Kitover et al., Reference Kitover, van Balen, Roche, Vandenberghe and Renssen2013). This mechanism dims the effects of the varying surface temperature.
Other effects that influence the subsurface temperature are surface conditions, for example solar insolation and vegetation effects (e.g. Chisholm & Chapman, Reference Chisholm and Chapman1992). In the Netherlands, changes in surface temperature due to variations in the surface energy balance, outside the built environment, are ∼1.5–2°C (e.g. Kooi, Reference Kooi2008).
Conclusions
We used a numerical model to study the effect of past climate changes on the thermal field in the upper crust. The effect of periodic changes in surface temperature due to climatic cycles extends to depths of 2–3 km: the higher the frequency of the changes in surface temperature, the lower the amplitude of changes in temperature at depth. Because of these cycles, the upper few kilometres of the subsurface thermal field are prevalently in a transient state.
The surface temperature history of the past 130,000 years in the Netherlands has resulted in a decreased geothermal gradient in the upper kilometres of the Dutch subsurface, and a slightly increased gradient at depths between 1 and 3 km. In addition, the climatic history before the Eemian is still visible in the surface thermal gradient of the Netherlands. Our results demonstrate that the upper 3 km of the Dutch crust are currently in a stage of heating.
Acknowledgements
We would like to thank Paul Andriessen, Hanneke Verweij and Danielle Kitover for useful discussions, and Damien Bonté for providing Fig. 5. The comments of two anonymous reviewers helped us to improve the paper.