Published online by Cambridge University Press: 19 March 2018
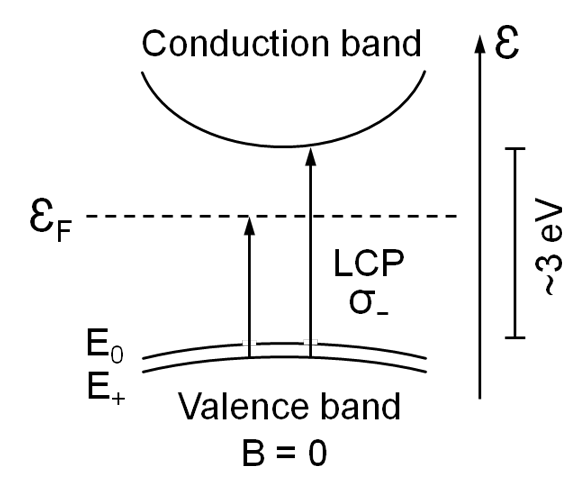
A longitudinal field component parallel to the wave vector is generally considered in nonlocal optical response. Longitudinal volume plasmons accompanied by inhomogeneous internal field optically break symmetry for isotropic metal nanoparticles. Here, natural circular dichroism in the interband transitions of TiN nanocubes, Au nanospheres, and Cu nanospheres in solution is presented. A field gradient or volume plasmons exert an electric force and consequently Lorentz force on bound valence-band electrons inside the nanoparticles. It is generalized that interband transitions in nanoparticles intrinsically produce a positive rotational strength and optical right-handedness. Electromechanical chiralty is introduced to explain the optical activity of achiral nanoparticles.
Present address: Department of Mechanical Engineering, Texas Tech University, Box 41021, Lubbock, Texas 79409, USA