Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Agosti, Amedeo
Natali, Mirco
Amirav, Lilac
and
Bergamini, Giacomo
2020.
Towards Solar Factories: Prospects of Solar‐to‐Chemical Energy Conversion using Colloidal Semiconductor Photosynthetic Systems.
ChemSusChem,
Vol. 13,
Issue. 18,
p.
4894.
Wang, Dong
Li, Yongsheng
Shi, Shujing
Tong, Xinwen
and
Yan, Zhengwei
2020.
Phase-field simulation of γ' precipitates rafting and creep property of Co-base superalloys.
Materials & Design,
Vol. 196,
Issue. ,
p.
109077.
Li, Xuejiao
Liu, Weihua
Tang, Zhongfeng
Xu, Tingrui
and
Wang, Jianqiang
2020.
Insight into dynamic interaction of molten MgCl2-NaCl-KCl with impurity water via FPMD simulations.
Journal of Molecular Liquids,
Vol. 314,
Issue. ,
p.
113596.
Singh, Karamvir
Singh, Bhoop
Sharma, Sandeep
Gupta, Monish
and
Tripathi, Chandra Charu
2020.
Performance Evaluation and Analysis of CNT for Strain Sensor applications.
p.
1.
Nemchen, Yelena
Hallford, Randal
and
Sharma, Preet
2021.
Types of potentials in a mitotic spindle.
Biochemistry and Biophysics Reports,
Vol. 27,
Issue. ,
p.
101076.
Chee, See Wee
Lunkenbein, Thomas
Schlögl, Robert
and
Cuenya, Beatriz Roldan
2021.
In situ and operando electron microscopy in heterogeneous catalysis—insights into multi-scale chemical dynamics.
Journal of Physics: Condensed Matter,
Vol. 33,
Issue. 15,
p.
153001.
Detmann, Bettina
2021.
Modeling chemical reactions in porous media: a review.
Continuum Mechanics and Thermodynamics,
Vol. 33,
Issue. 6,
p.
2279.
Liu, Chenxu
Tian, Yu
and
Meng, Yonggang
2021.
A Chemical Potential Equation for Modeling Triboelectrochemical Reactions on Solid–Liquid Interfaces.
Frontiers in Chemistry,
Vol. 9,
Issue. ,
Zhang, Kun
Wang, Fang
Cheng, Junliang
and
Zeng, Xiangguo
2021.
Multiphase-field modeling of disproportionation performance of ZrCo alloy during hydrogen absorption.
Materials Today Energy,
Vol. 22,
Issue. ,
p.
100857.
Zhang, Shujing
Xiao, Jiapeng
Chen, Xinyi
and
Li, Yu
2021.
Insulation and Flame Retardancy Improvement of PBDEs Using 3D-QSAR Model Combined with a Fuzzy Membership Function Method.
Chemical Research in Chinese Universities,
Vol. 37,
Issue. 3,
p.
729.
Li, Haoxin
Zhao, Xiaolin
Li, Yining
Gan, Yang
Qiu, Wujie
Wang, Jifen
and
Liu, Jianjun
2021.
Alkaline-earth metal substitution stabilizes the anionic redox of Li-rich oxides.
Journal of Materials Chemistry A,
Vol. 9,
Issue. 16,
p.
10364.
Hosseinzadeh, Reza
Khorsandi, Khatereh
Esfahani, Homa Sadat
Habibi, Masoud
and
Hosseinzadeh, Ghader
2021.
Preparation of cerium-curcumin and cerium-quercetin complexes and their LEDs irradiation assisted anticancer effects on MDA-MB-231 and A375 cancer cell lines.
Photodiagnosis and Photodynamic Therapy,
Vol. 34,
Issue. ,
p.
102326.
Palomino‐Asencio, Luz
Chigo‐Anota, Ernesto
and
García‐Hernández, Erwin
2022.
Insights on α‐Glucose Biosensors/Carriers Based on Boron‐Nitride Nanomaterials from an Atomistic and Electronic Point of View.
ChemPhysChem,
Vol. 23,
Issue. 24,
Korte-Kerzel, Sandra
Hickel, Tilmann
Huber, Liam
Raabe, Dierk
Sandlöbes-Haut, Stefanie
Todorova, Mira
and
Neugebauer, Jörg
2022.
Defect phases – thermodynamics and impact on material properties.
International Materials Reviews,
Vol. 67,
Issue. 1,
p.
89.
Wang, Yi
Lia, Frederick
Wang, Ke
McNamara, Kevin
Ji, Yanzhou
Chong, Xiaoyu
Shang, Shun-Li
Liu, Zi-Kui
Martukanitz, Richard P.
and
Chen, Long-Qing
2022.
A thermochemical database from high-throughput first-principles calculations and its application to analyzing phase evolution in AM-fabricated IN718.
Acta Materialia,
Vol. 240,
Issue. ,
p.
118331.
Palomino-Asencio, Luz
García-Hernández, Erwin
and
Chigo-Anota, Ernesto
2022.
Lauric acid adsorption on specific boron nitride fullerenes and the chemical influence of homonuclear bonds: a theoretical approach.
New Journal of Chemistry,
Vol. 46,
Issue. 22,
p.
10710.
Raza, Syed Hasan
Mittnacht, Tobias
Diyoke, George
Schneider, Daniel
Nestler, Britta
and
Klusemann, Benjamin
2022.
Modeling of Temperature- and Strain-Driven Intermetallic Compound Evolution in an Al-Mg System Via a Multiphase-Field Approach with Application to Refill Friction Stir Spot Welding.
SSRN Electronic Journal ,
Chen, Long-Qing
2022.
Chemical potential and Gibbs free energy II: Q&A.
MRS Bulletin,
Vol. 47,
Issue. 8,
p.
753.
Ji, Yanzhou
and
Chen, Long-Qing
2022.
Phase-field model of stoichiometric compounds and solution phases.
Acta Materialia,
Vol. 234,
Issue. ,
p.
118007.
Raza, Syed Hasan
Mittnacht, Tobias
Diyoke, George
Schneider, Daniel
Nestler, Britta
and
Klusemann, Benjamin
2022.
Modeling of temperature- and strain-driven intermetallic compound evolution in an Al–Mg system via a multiphase-field approach with application to refill friction stir spot welding.
Journal of the Mechanics and Physics of Solids,
Vol. 169,
Issue. ,
p.
105059.


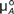

Chemical potential is a thermodynamics concept familiar to many, not only in materials science but also in physics, chemistry, chemical engineering, and biology. It is a central concept in thermodynamics of materials because all of the thermodynamic properties of a material at a given temperature and pressure can be obtained from knowledge of its chemical potential. Under the most common thermodynamic condition of constant temperature and pressure, chemical potential determines the stability of substances, such as chemical species, compounds, and solutions, and their tendency to chemically react to form new substances, to transform to new physical states, or to migrate from one spatial location to another.
Chemical potential is considered by many to be one of the most confusing and difficult concepts to grasp, although there appears to be no confusion about temperature, pressure, and electric potential. Chemical potential has been underappreciated and underutilized in applications of thermodynamics to materials science and engineering. One of the reasons for this is the widespread use of molar Gibbs free energy, partial molar Gibbs free energy, or simply Gibbs energy or Gibbs free energy but with the unit of J/mol. Adding to the confusion is the occasional use of Gibbs potential in place of Gibbs energy or Gibbs free energy, even when it refers to the Gibbs free energy of an entire system rather than on a per mole basis. Another reason why chemical potential is underappreciated is the surprising lack of a unique unit associated with such a quantity of central importance in the thermodynamics of materials.
The two main objectives of this article are to share the author’s understanding and interpretation of chemical potential and to make a case that it is the chemical potential, not the Gibbs free energy, that should be employed in the majority of applications of thermodynamics in materials science and engineering.
Definition of potentials
We start with the definitions of different forms of potentials in contrast to their corresponding energies. A potential in physics is defined as the energy stored per unit of matter (i.e., a potential describes the corresponding potential energy intensity). A potential is an intensive property independent of system size. For example, the familiar electric potential, ϕ, is the electrostatic potential energy, U E, with one unit (e.g., one Coulomb) of charge, q. In its simplest mathematical form, the electrical potential is defined as
Therefore, electrical potential represents the electrical energy intensity. Conceptually, it is fundamentally different from electrical energy, which is proportional to the system size and is an extensive quantity.
Another familiar example for potential is the gravitational potential or gravitational energy intensity, which is the gravitational potential energy per unit mass. Similarly, temperature, T, which can be considered the thermal potential or thermal energy intensity, is the thermal potential energy, U T, possessed by one unit of thermal matter, or one unit of entropy S
Pressure p can be considered as the mechanical potential. It is a measure of mechanical potential energy, U m, stored per unit volume V, or the mechanical energy intensity
Definition of chemical potential
Josiah Willard Gibbs formally introduced the concept of chemical potential approximately 140 years ago in his foundational article.Reference Gibbs1 Gibbs not only established the mathematical beauty of thermodynamics by formulating the fundamental equation of thermodynamics of a system but also introduced the concept of chemical potential, which he originally called the intrinsic potential. The establishment of the fundamental equation and introduction of chemical potential marked the birth of chemical thermodynamics and made it possible to apply thermodynamics to materials science and engineering.
In direct analogy to electrical potential, gravitational potential, thermal potential, and mechanical potential, the chemical potential of a chemical substance, μ, can be simply defined as the chemical energy (U c) possessed by 1 mol of the substance
where N is the number of moles of the substance (i.e., the chemical potential of a chemical substance represents its chemical energy intensity in a given homogeneous system or at a given location of an inhomogeneous system). The chemical energy U c is the same as the Gibbs free energy G, and Equation 4 holds for each chemical component of a homogeneous multicomponent solution as well as for the entire homogeneous solution.
The definition of chemical potential based on Equation 4 should be significantly easier to comprehend for most people, particularly for beginners in thermodynamics, than using derivatives or rate of increase in an energy function with respect to the addition of a substance, as is often the case. For example, in most textbooks, the chemical potential of a given species i is defined as the rate of increase in the internal energy of the system with respect to the increase in the number of moles of species i under constant entropy, constant volume, and constant number of moles for all species except species i. Alternatively, it is defined as the rate of increase in the Gibbs free energy of the system with respect to the increase in the number of moles of species i under constant temperature, constant pressure, and constant number of moles for all species except species i.
We can draw another analogy for chemical potential to thermal and electrical potentials. The application of an electrical potential difference between two spatial locations or an electrical potential gradient, also referred to as an electric field, results in electrical conduction, or the transport of electric charges. Imposing a difference in temperature between two locations or a temperature gradient leads to entropy or heat transfer from high-temperature to low-temperature regions. A difference in chemical potential between two locations or a chemical potential gradient is the driving force for the migration of the corresponding chemical species from high chemical potential regions to lower chemical potential regions.
Maxwell recognized the identification of temperature, pressure, and chemical potential as potentials more than 140 years ago: ‘‘The pressure is the intensity of the tendency of the body to expand, the temperature is the intensity of its tendency to part with heat, and the potential of any component is the intensity with which it tends to expel that substance from its mass.”Reference Baierlein2
It should be emphasized that one can associate a chemical potential with any type of substance. It can be a group of atoms, molecules, electrons, electron holes, atomic vacancies, phonons, or photons. The familiar Fermi level in semiconductor device physics or solid-state physics is the chemical potential of electrons.Reference Kittel3
Molar Gibbs free energy and chemical potential
To further understand chemical potential (μ) and establish the link between chemical potential and Gibbs free energy (G), we consider the total internal energy, U, of a simple system by adding up the thermal, mechanical, and chemical energy from Equations 2 to 4:
Gibbs defined a simple system as a system without considering the surface, electric, magnetic, and non-hydrostatic mechanical energy contributions.
Equation 5 is precisely the integral form of the fundamental equation of thermodynamics formulated by Gibbs by combining the first and second laws of thermodynamics,Reference Gibbs1 which connect the seven basic thermodynamic variables, U, T, S, p, V, μ, and N, of a simple system. We can rewrite Equation 5 in a different form as
Equation 6 is another form of the fundamental equation showing that the Gibbs free energy, G, is the chemical energy μN (Equation 4). If we write the chemical potential in terms of Gibbs free energy, we have
Therefore, the chemical potential of a substance introduced by Gibbs is simply the Gibbs free energy or chemical energy per mole of that substance (i.e., the molar Gibbs free energy is precisely the chemical potential).
Equation 7 suggests that there is no need to introduce the term molar Gibbs free energy. Instead, we should simply use the well-defined chemical potential to replace the term “molar Gibbs free energy” to clearly distinguish between “potential” and “energy.” The fact that we never get confused between electrical potential and electrical energy is because we never call the electrical potential the “molar charge electrical energy.” In electrostatics, we often solve for electrical potential or electric field, but we rarely compute electrical energy. For the same reason, we should have been working mostly with chemical potentials rather than chemical energy in applying thermodynamics to materials equilibrium and processes.
There is a general misconception that Equation 7 holds true only for pure substances or single-component systems. Equation 7 is true regardless of whether the substance is a single component or multicomponent. According to Gibbs, “for the purposes of defining chemical potential, any combination of elements in a given proportion may be considered a substance, regardless of whether it exists as a homogeneous body.”Reference Gibbs1
We can rewrite the integral form of the Gibbs free energy here for an n-component system,
where μ1, μ2, … μn are the chemical potentials of component 1, 2, …, and n, respectively, and N 1, N 2, … N n are the number of moles of component 1, 2, …, and n, respectively. In Equation 8, G = μN can be understood as the total Gibbs free energy or chemical energy of the substance, while μiN i can be considered the Gibbs free energy or chemical energy possessed by chemical component i in the substance. Therefore, the chemical potential μ of a homogeneous n-component system can be written in terms of chemical potentials for the n individual components, μ1, μ2, … μn,
where x i (= ${{N_i } \over N}$, where N = N 1 + N 2 +…+ N n) are mole fractions.
${{N_i } \over N}$, where N = N 1 + N 2 +…+ N n) are mole fractions.
In a simple interpretation, the Gibbs free energy per mole of the homogeneous system is the chemical potential of a homogeneous system at a particular composition (i.e., the chemical energy intensity). The chemical potential of a particular component is the Gibbs free energy per mole of that component in the homogeneous solution. For example, a substance can be a binary solution A xAB xB of composition x A and x B, with x A + x B = 1, μ = μAx A + μBx B.
The relationship among μ, μA, and μB can be illustrated using the well-known common tangent construction (see Figure 1). In most textbooks, the chemical potential μ of a solution A xAB xB is called the molar Gibbs free energy, Gibbs free energy, or Gibbs energy. This can be misleading, because chemical potential is not a form of energy—calling a potential as some sort of energy adds to the confusion and difficulty in understanding the concept of chemical potential.
Figure 1. Schematic illustration of the chemical potential µ of a binary solution A xAB xB and the chemical potentials µA and µB of the individual species A and B as a function of composition. $\mu _{\rm A}^o$ and
$\mu _{\rm A}^o$ and  $\mu _{\rm B}^o$ are the chemical potentials of pure A and pure B.
$\mu _{\rm B}^o$ are the chemical potentials of pure A and pure B.
Unit of chemical potential
The units for energy and for each of the familiar potentials are associated with the names of scientists who introduced or invented them. For example, the unit of energy is Joule; the unit of temperature, the thermal potential, is Kelvin (K); the unit of pressure, the mechanical potential, is Pascal (Pa); and the unit of electric potential is Volt (V) after Volta. However, essentially all textbooks and articles use J/mol (or eV/atom or eV/electron in the physics literature) as the unit for chemical potentials.
To be consistent with the units for the other potentials, it is useful to introduce a unique unit for the chemical potential. Since all the familiar potentials are associated with the names of the scientist who invented them and since Gibbs introduced this important concept of chemical potential, it is only natural and appropriate to adopt the unit “Gibbs” or “G” (Table I) as the unit of chemical potential to replace the unit of J/mol. FuchsReference Fuchs4 as well as Job and HerrmannReference Job and Herrmann5 already adopted the use of Gibbs as the unit for chemical potential.
Wide adoption of a unique unit for the chemical potential will be helpful for beginners to recognize the analogs of chemical potential to electric potential, temperature, and pressure. Assigning a unique unit for chemical potential will also help to identify whether a thermodynamic quantity is a potential or a form of energy. For example, while chemical potential is measured in Gibbs (=J/mol), Gibbs free energy is measured in Joules (J). Therefore, the molar Gibbs free energy or partial molar Gibbs free energy, which has the unit of J/mol (= Gibbs), should be identified as a chemical potential.
In summary, to facilitate the understanding of and promote applications of chemical potentials, the author makes the following recommendations:
▪ Introduce a simple definition for chemical potential: “chemical potential of a substance is the chemical energy per mole of the substance.” In this definition, Gibbs free energy is chemical energy, and the substance can be a pure substance or a multicomponent system.
▪ Use chemical potential to replace the terms “molar Gibbs free energy” and “partial molar Gibbs free energy” as well as “Gibbs energy,” “Gibbs free energy,” “free enthalpy,” and “Gibbs potential” when referring to the Gibbs free energy for 1 mol of a material with the unit of J/mol. If one would like to emphasize the amount of Gibbs free energy stored in 1 mol of matter, its unit should be J rather than J/mol.
▪ Use only the term “Gibbs free energy,” “Gibbs energy,” or “free enthalpy” when referring to the total Gibbs free energy or chemical energy of a material with the unit of J, and avoid using the term “Gibbs potential” to clearly distinguish potential from energy.
▪ Assign a unique unit name to chemical potential replacing its existing unit of J/mol to emphasize its analog to temperature, pressure, and electrical potential. This will also make it easier to recognize molar Gibbs free energy, which has the same unit as chemical potential, as a chemical potential.