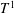 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}T^1$ AND
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}T^1$ AND 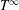 $T^{\infty }$
$T^{\infty }$Published online by Cambridge University Press: 15 May 2014
Tent spaces of vector-valued functions were recently studied by Hytönen, van Neerven and Portal with an eye on applications to 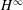 $H^{\infty }$-functional calculi. This paper extends their results to the endpoint cases
$H^{\infty }$-functional calculi. This paper extends their results to the endpoint cases 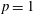 $p=1$ and
$p=1$ and 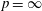 $p=\infty $ along the lines of earlier work by Harboure, Torrea and Viviani in the scalar-valued case. The main result of the paper is an atomic decomposition in the case
$p=\infty $ along the lines of earlier work by Harboure, Torrea and Viviani in the scalar-valued case. The main result of the paper is an atomic decomposition in the case 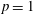 $p=1$, which relies on a new geometric argument for cones. A result on the duality of these spaces is also given.
$p=1$, which relies on a new geometric argument for cones. A result on the duality of these spaces is also given.