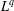 $L^{q}$-SPECTRUM OF SELF-SIMILAR MEASURES WITH OVERLAPS IN THE ABSENCE OF SECOND-ORDER IDENTITIES
$L^{q}$-SPECTRUM OF SELF-SIMILAR MEASURES WITH OVERLAPS IN THE ABSENCE OF SECOND-ORDER IDENTITIESPublished online by Cambridge University Press: 22 August 2018
For the class of self-similar measures in 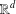 $\mathbb{R}^{d}$ with overlaps that are essentially of finite type, we set up a framework for deriving a closed formula for the
$\mathbb{R}^{d}$ with overlaps that are essentially of finite type, we set up a framework for deriving a closed formula for the 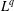 $L^{q}$-spectrum of the measure for
$L^{q}$-spectrum of the measure for 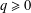 $q\geq 0$. This framework allows us to include iterated function systems that have different contraction ratios and those in higher dimension. For self-similar measures with overlaps, closed formulas for the
$q\geq 0$. This framework allows us to include iterated function systems that have different contraction ratios and those in higher dimension. For self-similar measures with overlaps, closed formulas for the 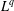 $L^{q}$-spectrum have only been obtained earlier for measures satisfying Strichartz’s second-order identities. We illustrate how to use our results to prove the differentiability of the
$L^{q}$-spectrum have only been obtained earlier for measures satisfying Strichartz’s second-order identities. We illustrate how to use our results to prove the differentiability of the 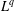 $L^{q}$-spectrum, obtain the multifractal dimension spectrum, and compute the Hausdorff dimension of the measure.
$L^{q}$-spectrum, obtain the multifractal dimension spectrum, and compute the Hausdorff dimension of the measure.
The authors are supported in part by the National Natural Science Foundation of China, grants 11771136 and 11271122, and Construct Program of the Key Discipline in Hunan Province. The first author is also supported by the Center of Mathematical Sciences and Applications (CMSA) of Harvard University, the Hunan Province Hundred Talents Program, and a Faculty Research Scholarly Pursuit Award from Georgia Southern University.